基于PVC 塑料异型材性能分析以优化断面结构*

耿金良，孟 凯，姜 宇，刘丽萍

（1.广东职业技术学院，广东 佛山 528041；2.宁波职业技术学院，浙江 宁波 315800）

我国在型材数量上位居全球之首，对塑料异型材的研究与工业发达国家还存在设计经验不足、缺理论支持。在当前形势下PVC 型材行业和塑料门窗行业要抓住机遇，实现快速发展。但目前还存在诸多问题。

现象1：PVC 塑料门窗在焊角强度方面存在质量问题。现象2：塑料门窗焊角强度合格与否检测不完善，缺少相应的质量制约机制。现象3：消费者对PVC 的质量产生怀疑。现象4：型材断面结构优化系统直接影响PVC 产品未来发展。

国内尚无真正意义上的PVC 塑料异型材断面结构优化系统，直接影响PVC 产品性能质量与行业发展[1]。如何求解真实产品的惯性矩与型材断面结构关系的特征，建立型材性能与焊角强度与型材结构三者关系的函数方程理论模型，旨在解决主动设计合理优化型材断面结构的瓶颈与核心技术问题。

1 惯性矩函数方程

1.1 建立数学模型

理论依据是在荷载作用下，构件的变形为弯曲变形。弯曲过程中，当坯料上作用有外弯曲力矩时，坯料的曲率半径发生变化[2]。因此，可利用简支梁原理导出型材惯性矩与焊角强度的函数方程的理论模型建立型材性能（应力σc）与焊角强度（最大力值Fc）与型材结构（惯性矩I）三者关系的函数方程理论模型。如图1 所示。

1.2 推导惯性矩方程

（1）如图（a）所示，由变形几何方程可知变形量为：

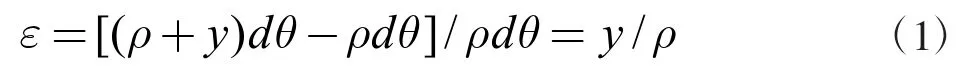
其中：ρ 为纯梁弯曲的曲率半径，y 为到中性轴的距离。

（2）胡克定律知正应力：

其中：E 为弹性模量。

（3）弯曲应力一般取最大值进行强度校核[3]。位于XY 平面内的弯矩 M 如图（b）所示。

由静力学关系知弯矩M 为：

公式（1）和（2）代入公式（3）可得：

（4）如图（c）所示，由型材受力分析可知，型材受力的弯矩力臂（受力点到通过C 点的正截面）为：

则型材受力的弯矩：

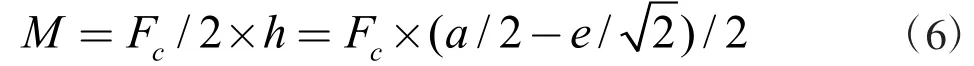
（5）由图（d）应力分布图可知，型材焊角断裂时，发生在 y=e，即 C 点处[4]，见图（c）。

综上可得出惯性矩函数方程：

图1 数学模型

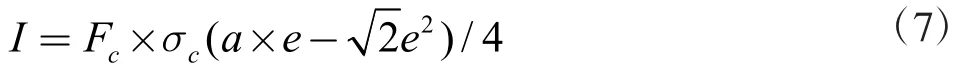
式中：

σc-受压弯曲应力（MPa）；

Fc-受压弯曲的最大力值（N），即经测角仪检测的最大力值（N）；

ɑ-试样支撑面的中心长度（mm）；

e-临界线AA'与中性轴ZZ'的距离（mm）；

I-型材横断面ZZ'轴的惯性矩（mm4）；

2 确定数学模型参数

根据型材剖面的外形尺寸和壁厚计算出型材惯性矩与实际生产出来的真实型材存在一定的误差。如图2 所示。

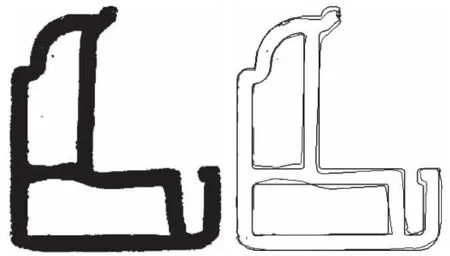
图2 真实型材断面与矢量化型材断面对比

利用Vpstuio/Scan2Dwg 量化软件对型材真实断面进行精确测量[5]，在 Autocad 软件中应用“面域/质量特性”工具（命令）求解惯性矩[6]。

（1）首先按实际比例精确绘出型材的断面图

（2）Command：region

（3）Command：Subtract

（4）Command：massprop

可将质心移动到坐标原点，可得：

e=35.2930mm，I=199048.0488mm4

3 系统开发

3.1 焊角强度检测系统

开发系统软件，如图3 所示。型材断面图可自动显示；输入测角仪上显示的力值（Fc），系统自动显示与之对应的弯曲应力值（σc），进而确定参数导入真实产品的惯性矩值。

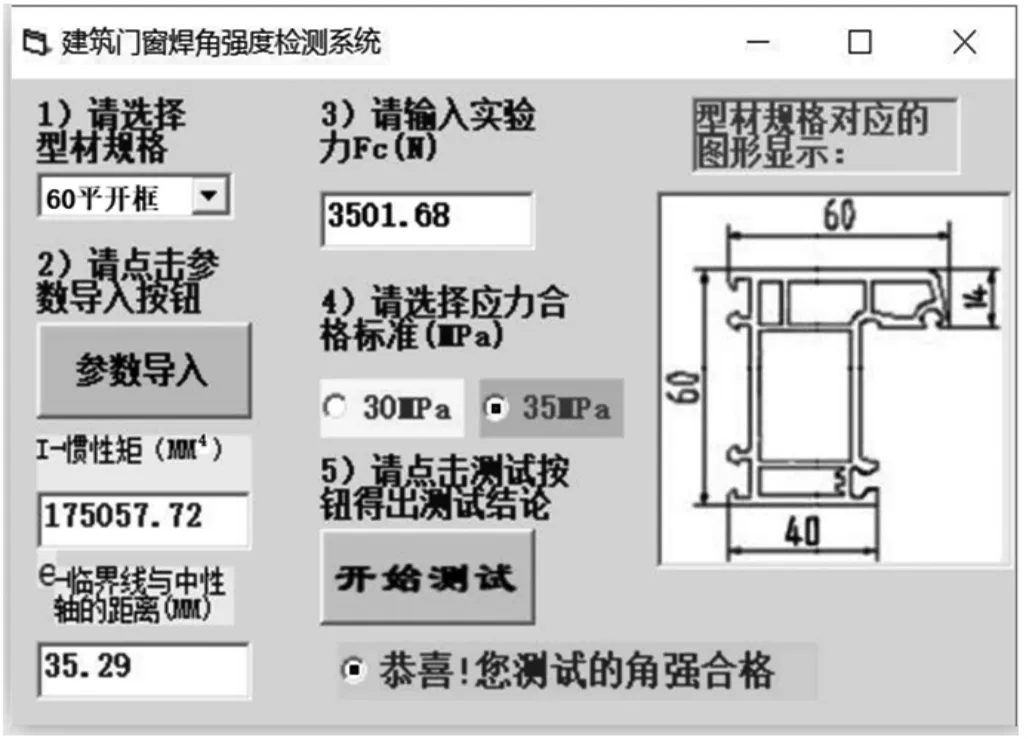
图3 焊角强度测试对话框

部分源代码如下：

3.2 PVC 型材断面优化系统

利用AutoLISP 语言、对话框控制DCL 语言进行参数算法与数据传递[7]，可视化对话框如图4 所示。

通过输入型材断面结构参数尺寸，系统自行显示该规格型材的惯性矩值。因此在满足型材性能与焊角强度的前提下，从而确定了型材断面结构参数尺寸，达到优化断面结构的目的。

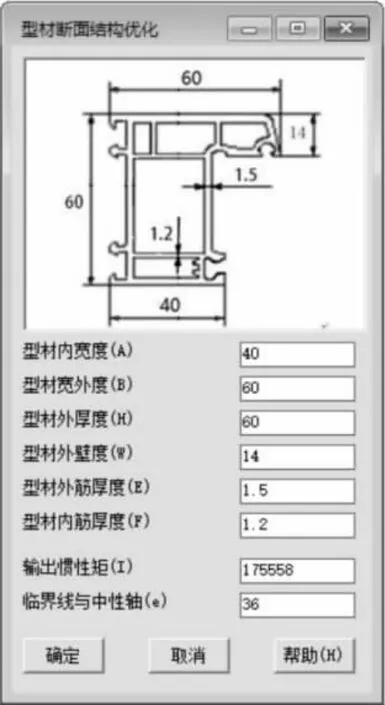
图4 尺寸驱动法对话框

部分源代码程序如下：

4 结束语

通过验证焊角强度合格的惯性矩所优化PVC 型材断面结构必满足型材性能要求的结论，与过去从断面设计-生产准备-小批量试生产-型材性能检验-正式生产的循环往复的工作过程相反，无需试生产。通过“焊角强度-惯性矩-型材断面结构三者内在机理”的研究，得出优化后的型材结构必满足合格焊角强度的理论。实现型材生产行业与门窗制造行业开发新产品需求，为PVC 型材行业和门窗制作行业的发展提供理论基础与应用价值，具有重大的社会效益和现实意义。