基于仿射算法的电路与系统可靠性研究*

丁同禹，王孟于

（集美大学 信息工程学院，福建 厦门 361021）

引言

随着电子与远程通信技术的飞速发展，电子电气设备与系统的集成度不断提高，其在制程及使用过程中受工艺或外界电磁干扰影响而产生参数不确定性（parameter uncertainty）的现象日益严重[1-3]，比如，设备、元件及线路在长期使用后发生老化；各种外界因素（温度，空气湿度，静电放电等）对元件、线束造成性能改变或损坏等。一旦这些内部或外界的干扰因素造成了设备或元件电参数（如微带线的介电常数）的变化，将会直接影响整个系统的性能，造成电路或系统可靠性的下降和安全系数的大幅降低。

不仅如此，不确定参数问题还会对电磁信号传播特性的研究造成危害，尤其是室内环境的无线信道建模。在利用射线追踪（ray-tracing）、时域有限差分（FDTD）等方法建立指定室内场景无线信道模型时，目标环境中的不确定参数（如空气湿度导致的建筑物墙体电导率及介电常数变化，施工过程产生的建筑物几何尺寸误差等），会在信道模型中引入大量的随机变量，导致该模型的输出（如路径损耗等）变成不确定的范围区间，从而降低模型可信度，严重影响其在无线系统布局及优化中的应用价值。

因此，当电路、元件或电磁环境中某一媒质的电磁参数发生变化时，亟需对系统响应的随机特性进行预测和评估，有效地降低不确定参数对电路与系统可靠性造成的危害；在信道建模研究等领域则可获取更为完整的电波传播特性数据和信息，提高无线信道模型的可信度。

1 最坏分析算法

最坏分析算法作为一种高效的数值仿真技术能够准确分析不确定参数系统的随机特性并预测其响应（输出）的变化范围，不仅可为电路系统的可靠性评估提供依据，还能缩短研发周期，提高设备与系统的安全系数[4]。用于不确定参数系统分析的传统数值技术大都以概率类算法为基础，如以Monte Carlo算法为代表的基于抽样理论的系列方法，通过大量的随机试验来覆盖不确定参数可能出现的所有取值，从而不断接近所要预测的真实边界，其缺点是当不确定参数变化范围较大时，所需的样本数量异常巨大，导致效率急剧下降（Monte Carlo算法的收敛速度为为样本数量），即便如此，其预测结果仍然可能出现遗漏真实值的情况。

相比之下，基于最坏分析算法的数值技术以绝对保守的方式对系统输出进行预测，其所提供的预测结果能够覆盖所有的真实情况，即“始终包含全部可能出现的真实结果”，不会产生任何遗漏，从而提供比经典的概率类算法更加可靠的预测结果。同时，最坏分析类算法的收敛速度在变量数相对较少时远大于概率类算法，在效率上也具有明显的优势。

2 仿射算法的基本原理

作为最坏分析算法的典型代表，仿射算法（affine arithmetic，AA）的概念在20世纪90年代由Comba和Stolfi首次提出[5]。仿射算法能够实现对预测对象浮动范围的保守估计，即直接预测电路与系统可能出现的最坏情况。该算法从区间算法（interval analysis）变形而来，因此也能够自动记录浮点的截尾和舍入误差。此外，仿射算法增加了一些附加的噪声系数，若多个仿射形式有相同的噪声系数，那么证明两者具有关联性，仿射形式之间关联性和依赖性可以根据变量之间相同噪声系数的多少决定。这种明确变量之间关联性的方法，有助于辨别计算过程中所记录的各个不确定参数的依赖关系，如果变量之间的噪声系数呈负相关时，可以通过计算变量相互抵消达到减小区间扩张值的目的，得到更小的区间结果，提高计算结果的准确性，同时缩短计算时间。

在区间算法中，变量是使用两个临界点的极值来表示，例如，x¯=[a，b]代表一个变量 x，其取值范围落在区间[a，b]之内。该方法的主要缺陷是无法捕捉到各个变量之间的关系，从而导致对真实区间边界的“高估”。仿射算法对不确定参数的表达形式进行了修订，同样对于一个区间变量 x∈[a，b]，其对应的 AA 变量表达为：x˜=x0+x1ϵ，其中 x0=（a+b）/2，而 x1=（b-a）/2 称为其“半径”，噪声系数 ϵ是一个取值范围始终在±1之间的独立区间变量。可见，相比于传统的区间算法，仿射算法在运算过程中考虑了变量之间的关联，并将其引入到计算链中，从而有效消除了变量裕量叠加所引起的过度估计，对于任意一个给定的含有n个不确定因素的随机变量，其仿射表达形式为：

在此定义下给出的变量x˜的最坏边界为（上下边界）：x0±Σi|xi|。若已知两个独立的区间变量：x˜和y˜，其仿射形式的乘法运算如公式（2）所示。

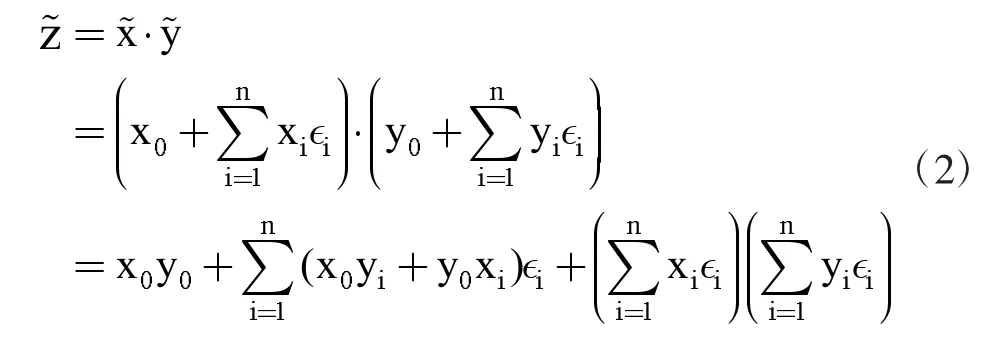
显然地，在此过程中产生了一个新的高阶项。为了消除该项所引入的计算复杂度，引入一个新的变量：ζ。令：

3 基于仿射算法的矩阵运算

3.1 参数矩阵求逆

矩阵求逆是电路频域求解过程中十分关键的一项内容。对于仿射形式的变量矩阵，其求逆运算需要结合其他数值算法，为了叙述简便，本文只讨论一个不确定因素的情况，例如求解：

其中，X0是中心矩阵，X1代表不确定干扰因素ϵ1的“半径”矩阵。当X1的秩为1时，使用Sherman Morrison公式对其求逆，过程如式（5）所示。

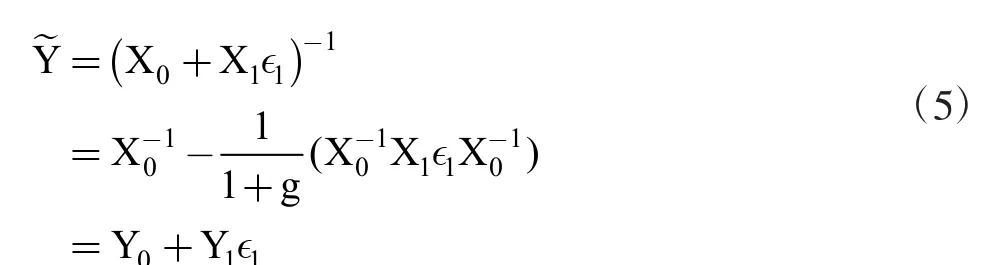
则需要将其拆分成若干个秩为1的子矩阵的加和形式，然后逐项使用公式（5）完成求逆运算。

3.2 参数矩阵的指数运算

集总和分布式电路求解过程中经常使用到的另一项运算就是求矩阵指数。本文使用了bilinear近似公式作为辅助技术，完成仿射形式的矩阵指数运算，如公式（7）所示：

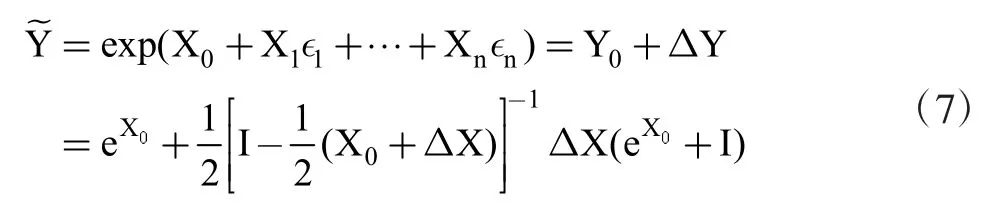
其中，I为单位矩阵，Y0=exp（X0）为新的中心矩阵，ΔX=X1ϵ1+…+Xnϵn为原矩阵的全部干扰项。进一步化简ΔY可得：

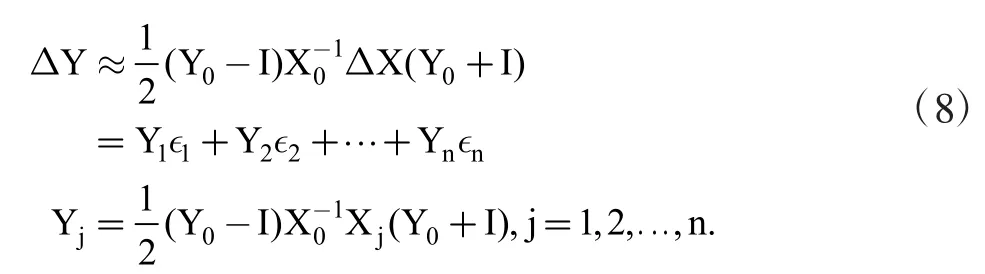
4 不确定参数电路的时域分析

本节应用仿射算法完成一个元件参数为不确定量的RLC电路的时域仿真和分析，电路图如图1所示。其中，L=1mH，RL=0.5Ω，C=10μF，RC=0.5Ω，R=20Ω。设电容 C 存在±50%的容差，应用仿射算法预测输出（电感电流iL（t））的响应范围。

图1 含有不确定参数元件的RLC电路

首先对该电路的状态方程：x˙（t）=Ax（t）+bu（t）（其中状态向量x（t）=[iL（t），vC（t）]T为电感电流和电容电压，且x（0）=[0，0]T）进行时间离散：

其中，

以上公式中的a//b表示并联：a·b/（a+b）。

应用上文所述的仿射算法数值结构，依次完成本电路求解运算中所需要的对参数矩阵A的求逆和指数运算，并解得仿射形式的电感电流iL（t）在时域的输出波形如图2所示。

如图2所示，本文所使用的基于仿射算法的数值架构能够有效预测在RLC电路的电容值出现变化时，电路的时域输出波形可能产生的变化，并成功估计了电感电流在时域可能出现的最大值和最小值两种极端情况。为了验证算法的有效性，与经典的Monte Carlo随机试验方法（图2灰色实线）进行了对比验证，结果表明仿射算法（图2黑色实线）的预测范围准确，同时在Matlab环境下运行时仿真速度达到Monte Carlo算法（10000次随机试验）的3倍以上。

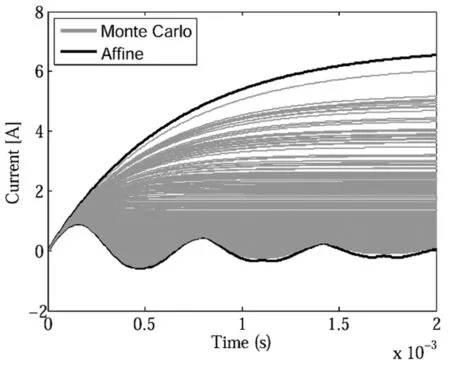
图2 电感电流iL（t）的预测结果

5 结束语

以电路与系统的可靠性预测为目标，本文对一种典型的RLC电路进行了基于仿射算法的最坏分析。该研究通过将仿射算法与其他数值技术，如Sherman Morrison公式，bilinear数值近似等技术结合，解决了仿射形式矩阵的运算问题，进而求解了目标电路的电容元件参数发生变化时，系统响应的变化范围。该预测结果与经典的Monte Carlo方法进行了对比，不仅达到了较高的精度，且在运算效率上得到了显著提高。