流动与传热数值计算通用控制方程的研究

李敬法，石国赟，陈宇杰，宇 波

(1.北京石油化工学院机械工程学院，深水油气管线关键技术与装备北京市重点实验室，北京 102617；2.中国石油大学(北京)机械工程学院，北京 102249；3.西安交通大学能源与动力工程学院，陕西 西安 710049)

随着计算机技术的进步和数值计算方法的发展，流动与传热数值模拟在工程领域和科学研究中得到越来越广泛的应用。为进行模块化编程和方便结果分析，通常将不同物理问题的控制方程写成由非稳态项、对流项、扩散项和广义源项组成的通用控制方程形式[1-2]。通用控制方程简化了原方程的复杂形式，使不同类型的控制方程具有相似的表达形式，大大提高了相似程序模块的通用性和整体编程效率，有利于探索不同问题的共同特征，深化理论研究。因此，通用控制方程深受流动与传热数值计算研究者的青睐[3-5]。

为了得到真实的数值模拟结果，首先需要保证物理问题控制方程的准确性。但目前通用控制方程多用于常物性参数并忽略摩擦效应的场合，针对变物性参数和考虑摩擦效应情形下的通用控制方程研究较少。在多数情况下，为了进一步简化计算、降低编程实施的复杂度，研究者们通常忽略物性变化和摩擦效应对计算结果的影响。对于绝大多数常物性、黏度较小、流场变化不是很剧烈的物理问题，这种处理对最终计算结果的影响甚微。但对某些黏度变化大、流场变化剧烈、物性参数在空间存在突变或剧烈变化的物理问题，这种处理会对计算结果产生一定影响，严重时甚至会导致计算结果失真。如原油在大型浮顶油罐中储存时，受太阳辐射、环境因素等影响，不同油层的温度会存在一定差异。由于原油黏度受温度的影响较大，导致油罐内不同位置处的原油黏度不同。若在大型储罐温度场的数值模拟研究中将油罐内原油黏度当作常数处理，计算结果会与实际情况产生一定偏差，最终对原油的周转调度和加热方案等产生影响[4，6]。

基于此，笔者对流动与传热通用控制方程进行了进一步深入研究，探讨了通用控制方程是否考虑物性参数变化和摩擦效应对数值模拟结果的影响。重点分析了动量方程中由黏度变化引起的附加项和能量方程中由摩擦作用产生的附加热源项对数值计算结果的影响规律，并通过2个经典算例对上述分析进行验证和说明。

1 通用控制方程分析

流动与传热数值计算常用的通用控制方程形式为[7-8]：

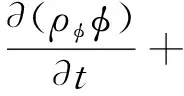
(1)

式中：φ为通用变量，可表示速度、温度、组分质量浓度等；ρφ为广义密度；Γφ为广义扩散系数；U表示速度矢量；Sφ为广义源项，通常情况下不能归入前3项的项均可归入广义源项中。当φ表示不同的变量时，ρφ、Γφ和Sφ的具体表达式也会发生相应变化。

以层流流动与换热为例，连续性方程、动量方程和能量方程的表达式分别为：

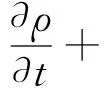
(2)

μ(U)T]+

(3)

μ(U)T]·U+[μU+μ(U)T]·U-

(4)

将方程(2)～(4)改写成通用控制方程(1)的形式：

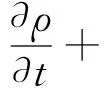
(5)

(6)

(7)

其中：动量方程的广义源项SU=·[μ(U)T]+·U)+ρf-p；能量方程的广义源项ST=·[μU+μ(U)T]·U+[μU+μ(U)T]·U-·U-p)·U+Sh。

1.1 物性参数的影响

方程(5)～(7)中的物性参数主要有密度、黏度、比热容、导热系数等。文献[3，7-8]中已专门讨论过非常数比热容的影响，这里不再赘述。由于工程实际中常见的流体多为不可压缩流体，这里也不再讨论密度的影响。因此，对于不可压缩流体流动，式(6)中的广义源项可进一步简化为：

SU=·[μ(U)T]+ρf-p

(8)

为简化计算和方便编程，研究者们通常忽略式(8)中由黏度变化产生的附加项·[μ(U)T]。分析式(8)可知，当黏度为常数时，·[μ(U)T]为0。因此，对于绝大多数流体黏度为常数或黏度变化非常小的物理问题，·[μ(U)T]对最终计算结果的影响甚微，基本可忽略。但当流体黏度变化剧烈时，这种近似处理会对计算结果产生一定影响，此时一般不能忽略·[μ(U)T]。

对于导热系数λ，无论λ是否为常数，均对扩散项·(λT)和数值计算结果无影响。

1.2 摩擦效应的影响

对于不可压缩流体流动，式(7)中的广义源项可进一步简化为：

ST=[μU+μ(U)T]·U+Sh

(9)

由式(9)可知，能量方程的广义源项包含摩擦做功产生的附加热源项和内热源项。为简化计算和便于编程，摩擦做功产生的附加热源项[μU+μ(U)T]·U常被忽略。分析该项可知，对于流体黏度较小、流场变化不剧烈的物理问题，[μU+μ(U)T]·U的数值较小，因此对计算结果的影响较小。但当流体的黏度很大、流场变化剧烈时，[μU+μ(U)T]·U的值较大，会对计算结果产生影响，此时该项在数值计算中不应该被忽略。

2 算例验证

2.1 物性参数的影响

以流动与传热数值计算的经典算例—封闭方腔自然对流为例，分析动量方程中由黏度变化产生的附加项对模拟计算结果的影响。这里需要指出的是，为了更好地说明黏度变化对计算结果的影响，本算例不考虑能量方程中摩擦效应的影响。计算区域示意图如图1所示，方腔边长l=0.01 m，上、下边界为绝热边界条件，左、右边界为恒温边界条件，其中Th=60 ℃、Tc=0 ℃，所有边界均为无滑移边界。采用2种不同性质的流体作为方腔内的流动工质，物性参数如表1所示。采用64×64的均分网格划分计算区域，采用有限容积内节点法离散控制方程，采用SIMPLE算法进行压力-速度耦合计算，详细数值求解步骤及算法介绍参见文献[9-11]，这里不再赘述。

表1 流体物性参数表

对于自然对流问题而言，工程实际中最关注的是温度场的分布。方腔温度场等值线对比图如图2所示，其中红色实线表示考虑黏度变化产生附加项时的计算结果，蓝色虚线表示不考虑黏度变化产生附加项时的计算结果。从图2中可明显看出，对于本算例的2种流体工质，当流体黏度随温度发生变化时，考虑和不考虑黏度变化产生的附加项时得到的温度等值线不完全重合，尤其是在中间位置处两者偏差较明显。说明黏度变化产生的附加项对计算结果有一定影响。因此，当对计算精度要求较高时，为得到准确的数值解，需考虑黏度变化产生的附加项对最终数值计算结果的影响。

方腔垂直中心线处的温度分布对比图如图3所示。与图2类似，2种情况的温度分布不能完全重合，说明黏度变化产生的附加项对计算结果会产生一定影响。此外，还可观察到相同位置处考虑黏度变化产生附加项时的温度值要高于不考虑黏度变化产生的附加项时的温度值，原因是黏度变化产生的附加项相当于一个内热源，在计算区域内产生了热量。所以，考虑黏度变化产生的附加项时，计算区域流体的温度会升高。

为定量说明考虑黏度变化产生的附加项影响，计算了图3方腔垂直中心线温度分布曲线的平均相对误差和最大相对误差，结果如表2所示。其中，平均相对误差和最大相对误差的计算式分别为:

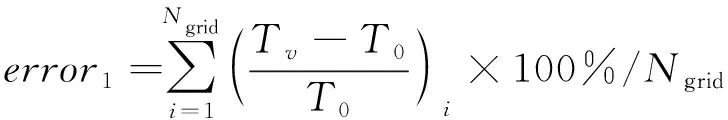
(10)

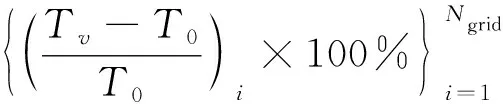
(11)

式中：Ngrid表示方腔垂直中心线方向的节点数；Tv表示考虑黏度变化附加项时的温度；T0表示不考虑黏度变化附加项时的温度。

由表2中的数据可知，黏度变化产生的附加项对数值计算结果会产生一定影响，但这种影响不大。本算例方腔垂直中心线上的温度最大平均相对误差和最大相对误差分别为1.26%和1.78%。而且还可发现，当黏度变化剧烈时，平均相对误差更大。

表2 方腔垂直中心线处温度误差

2.2 摩擦作用的影响

以流动与传热数值计算的另一个经典算例—封闭方腔混合自然对流为例，分析能量方程中摩擦作用产生的附加热源项对模拟计算结果的影响。这里需要指出的是，为了更好地说明摩擦作用对计算结果的影响，本算例不考虑动量方程中物性参数非常数的影响。计算区域示意图如图4所示。方腔边长l=0.01 m，上、下边界为绝热边界条件，左、右边界为恒温边界条件，其中Th=50 ℃、Tc=0 ℃，顶盖拖动速度为ulid，其余边界均为无滑移边界。采用某流体作为方腔内的流动工质，物性参数如表3所示。采用与算例2.1完全相同的网格数、离散方法以及数值算法进行求解，这里不再赘述。

表3 流体物性参数表

方腔温度场等值线对比如图5所示，其中红色实线表示考虑摩擦作用产生附加项时的计算结果，蓝色虚线表示不考虑摩擦产生附加项时的计算结果。由图5可知，在一定的方腔顶盖拖动速度和较大的流体黏度下，是否考虑摩擦作用产生的附加项对计算区域温度分布规律有较大影响，尤其是方腔中心位置处存在较大偏差。因此，当流场变化较剧烈且流体黏度较大时，需考虑摩擦作用产生的附加项对最终数值计算结果的影响。从图5还可看出，不同的顶盖拖动速度、流体黏度对数值计算结果的影响不同。

方腔垂直中心线处的温度分布对比图如图6所示。对比图6(a)和图6(c)可发现，顶盖拖动速度对两者温度等值线分布差异具有重要影响。在流体黏度不变的情况下，当顶盖拖动速度从0.1 m/s提高到0.5 m/s时，流场的变化变得更加剧烈，考虑摩擦作用影响和不考虑摩擦作用影响的温度分布偏差显著增大。对比图6(b)和图6(c)可发现，在顶盖拖动速度不变的情况下，流体黏度对两者温度等值线分布也具有重要影响。当流体黏度从5 Pa·s提高到15 Pa·s时，考虑摩擦作用影响和不考虑摩擦作用影响的温度分布偏差增大，但增大的幅度比顶盖拖动速度弱一些，这是因为此时流体黏度已经较大，黏度对计算结果的影响比顶盖拖动速度弱一些。此外，考虑摩擦作用时的温度值要高于不考虑摩擦作用时的温度值，原因是摩擦作用产生的附加项相当于一个内热源项，所产生的热量提升了计算区域的整体温度。因此，考虑摩擦作用产生的附加项时，计算区域流体的温度会升高。

为定量说明考虑摩擦作用产生的附加项影响，计算了图6方腔垂直中心线处温度分布的平均相对误差和最大相对误差，如表4所示。由表4中可以看出，摩擦作用产生的附加项对数值计算结果产生重要影响，当顶盖拖动速度为0.5 m/s、流体黏度为15 Pa·s时，方腔垂直中心线上的温度最大相对误差高达70.35%。而且当流场变化剧烈程度增大或流体黏度增大时，相对误差会变得更大，在本算例条件下，流场变化对相对误差的影响比流体黏度对相对误差的影响更显著。因此，当流体黏度较大且流场变化较剧烈时，数值计算应考虑摩擦作用产生的附加项，否则会使计算结果失真。

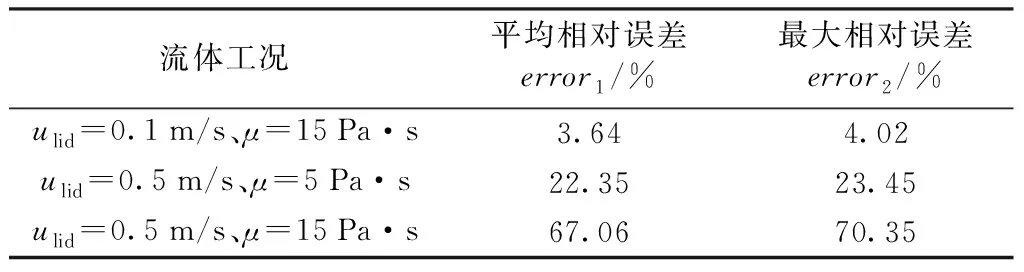
表4 方腔垂直中心线处温度误差

3 结论

分析和推导了通用控制方程中考虑物性参数变化和摩擦效应时的附加源项，探讨了物性参数变化和摩擦效应对通过控制方程计算结果的影响，得出如下结论：

(1)目前常用通用控制方程一般只适用于黏度为常数的情况。当流体工质的黏度不是常数且流场变化较剧烈时，动量方程中由于黏度变化产生的附加项相当于一个内热源项，会对计算结果产生一定影响。在进行精确数值模拟时，可考虑此项的影响。但相比摩擦作用的影响，黏度变化的影响相对较弱。

(2)目前常用通用控制方程一般未考虑摩擦作用的影响。当流体工质的黏度较大且流场变化剧烈时，能量方程中由于摩擦作用产生的附加项不可忽略。该项相当于一个内热源项，会对计算结果产生较大影响，严重时甚至导致计算结果失真。