基于包络预测的动态阈值计层算法

戴政豪，高世桥，李泽章，张铱翔

(北京理工大学 机电学院， 北京 100081)

现代战争中，随着不同形式的高价值目标如机库、航母、弹药库、指挥控制中心等的出现以及防御工事防护能力的不断提高，为了对这些处于高防护能力下的高价值目标产生最大的毁伤效果，出现了硬目标侵彻武器[1]。硬目标侵彻武器中起着至关重要作用的核心部件是硬目标侵彻引信。在高过载条件下，硬目标侵彻引信可以自适应控制炸点实现对目标最大的毁伤效果。其一般利用高g值加速度传感器来感知弹丸在侵彻目标的过程中受到来自目标的阻力所产生的减加速度，以此信息为基础实现弹丸侵彻状态识别。按起爆策略划分，硬目标侵彻引信主要分为计时起爆引信、空穴识别起爆引信、计层起爆引信、计行程起爆引信、定深起爆引信和介质识别起爆引信6种[2]。

国内的侵彻引信起爆控制技术研究主要集中在计层起爆控制方面，这种控制方式利用加速度传感器采集弹体的加速度信息，当弹体克服阻力穿过硬目标时，其采集到的信号将会显示出特殊的穿层特征，计层起爆方式就是根据这个特征来进行层数识别的。当弹体侵彻速度较低时，信号的穿层特征较为明显，容易实现层数识别；当弹体速度较高且层间距较近时，由于加速度传感器所记录的侵彻过载信号未明显衰减，与下一层过载信号混叠从而产生信号粘连的现象[3]，此时用传统的阈值判别方法往往会导致误计层。针对信号粘连与混叠的问题，国内许多研究者也从各种方面提出了许多方法，如机械滤波[4-5]、低通滤波[6-7]、自相关算法[8-11]、融合算法[12]、时频分析法[13-14]等。这些算法均为在层数识别之前对信号进行滤波，来排除加速度传感器中的高频噪声及弹体中来回反射的应力波给层数识别造成的干扰，然而，其层数识别均采用固定阈值法。

本文通过分析侵彻过载信号的指数衰减振动特征，以此为基础提出一种基于包络预测的动态阈值计层算法。该算法除了第一层直接采用一个比较小的阈值进行识别以外，后续层数以相对上一层包络线偏离一个相对阈值为依据来进行层数识别。

1 侵彻信号特征分析

侵彻弹的加速度传感器可以简化为一个单自由度系统[15]，如图1所示。其运动微分方程为

图1 单自由度系统示意图

(1)

其中:m为质量，c为粘性阻尼系数，k为弹性系数。令

(2)

其中:ω0为相应的无阻尼时的固有频率，n为衰减系数。

则式(1)可表示为

(3)

对于欠阻尼系统，n<ω0，此微分方程的解为

x=Ae-ntsin(ωdt+φ)

(4)

对上式求两阶导数，可得加速度为

(5)

因此，加速度和位移一样，都是衰减振动曲线，如图2所示。其包络线方程都可写成如下形式：

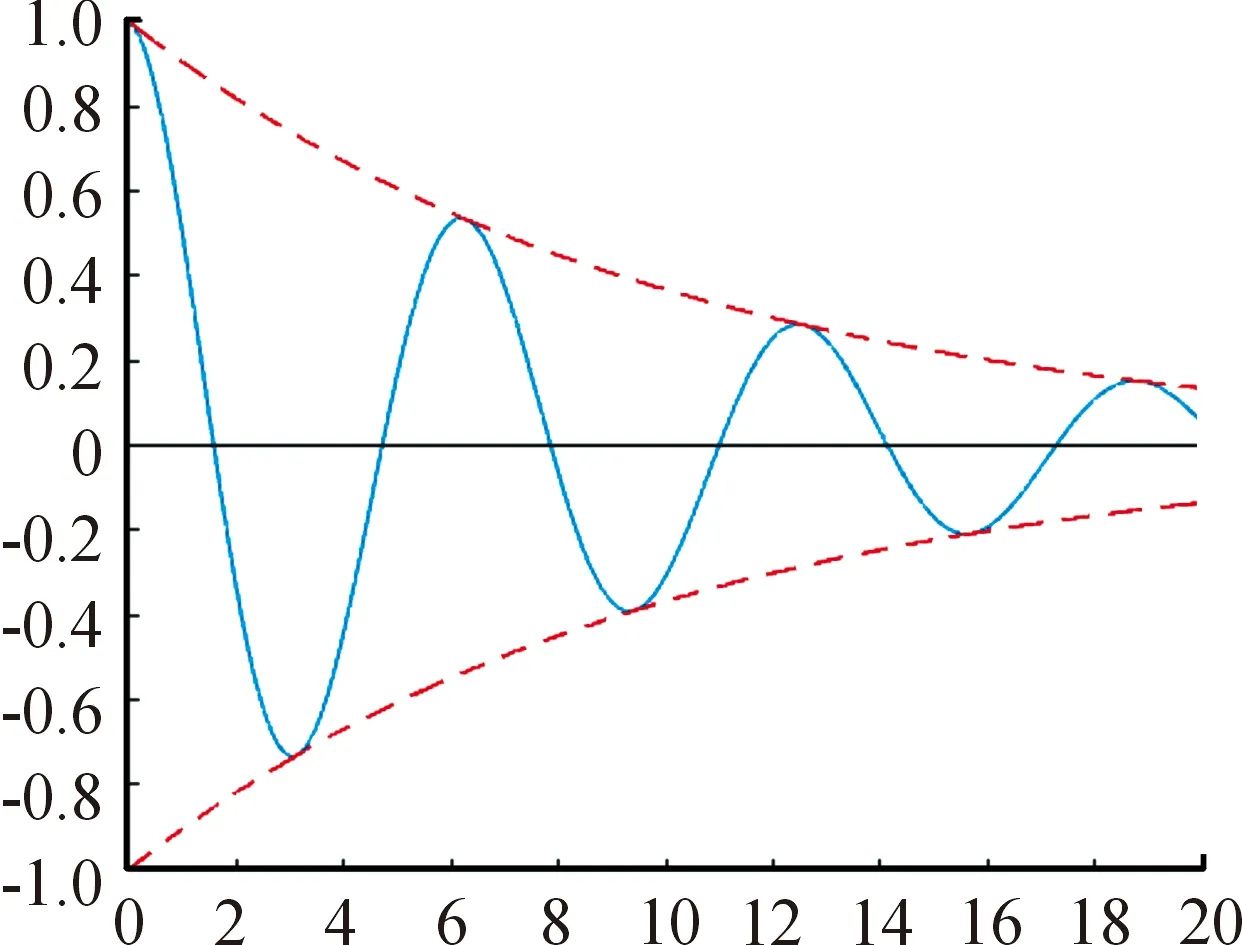
图2 衰减振动曲线及其包络线

g(t)=Be-rt

(6)

由式(6)可知：包络线方程仅由参数B和r决定。一般地，仅获取两个数据点就可以完全确定此方程。为了减小信号随机性带来的误差，本算法采用N个数据点来拟合出更加准确的包络线表达式。对式(6)取对数可得：

ln[g(t)]=lnB-rt

(7)

这样就可以使用最小二乘法对上式进行线性拟合。已知N个数据点y1,y2，…，yN，对应时间点为t1,t2，…，tN。根据最小二乘法原理，写出以下方程组：

(8)

该式为线性方程组，解此线性方程组就可得到由数据拟合而成的衰减信号包络线方程。

弹体在侵彻过程中弹头撞击一层靶板所受到一个瞬态冲击会使加速度计偏离平衡位置开始振荡，在冲击结束后振荡开始在阻尼的影响下按照式(6)方式进行衰减。如前所述，在高速侵彻多层硬目标中由于信号还未完全衰减就进入下一次穿靶，这就造成了一定的信号粘连与混叠现象，直接使用固定阈值判别法将可能导致误计层。因此，如果可以利用信号衰减的特征，以其包络线作为基准来进行下一层的判别，将有效克服简单固定阈值法带来的误计层问题。

2 包络预测的动态阈值计层算法

在传统的阈值识别法中，为了避免由于信号反复振荡多次穿过阈值而导致的误计层问题，在计一层之后，会加上一个时间窗，在这个时间窗里不进行层识别。但这种方法依然无法保证在时间窗结束后未充分衰减的信号不再穿过阈值，从而导致多计层问题；为了保证阈值在未充分衰减的信号之上，需要将阈值尽量设置得高一些，但阈值设定得太高又无法保证真正的穿层信号能够穿过阈值，这就容易导致漏计层的问题。在后期的仿真中可以明显看到这种缺陷。

为了解决这个矛盾，本文引入根据衰减信号特征拟合的包络线，提出一种以此包络线为基准来进行层数识别的方法。包络预测的动态阈值算法是基于侵彻过载衰减信号包络线的特征，在此特征的基础上加上一个相对阈值来实现对层数的识别。相对阈值主要考虑实测信号中杂波等干扰信号的影响，依据侵彻弹穿层前所采集信号的最大幅值来确定。该算法在识别出一层后，先加上一个长时间窗，并将其平均分成多个小时间窗，在每个小时间窗内计算平均值，以此为已知点根据式(8)来拟合包络线，并给此包络线加上一个相对阈值构成动态阈值线，以此来判断之后的信号是否为新的穿层信号。算法流程如图3所示。

图3 算法流程框图

具体算法流程如下：

1) 为降低误差，将所有信号取绝对值，正负信号共同参与包络线拟合。

2) 开始时，设定一个比较低的阈值(该阈值仅用于第一次识别，其大于未穿层前最大干扰信号即可)，当侵彻信号超过此阈值时，计第一层。

3) 在计一层之后，加上一个时间窗，将其平均分成N个小时间窗，在每个小时间窗内算出对应时间窗内的平均值Si和标准差σi，根据3σ原则将Si+3σi作为拟合包络线的数据点，对应时间点ti取在时间窗中点。

4) 利用得到的数据点通过式(8)拟合出包络线方程，并加上相对阈值作为最终的动态阈值。

5) 判断时间窗之后的信号是否超过动态阈值，以此来判别是否到达下一层穿靶。

6) 如果识别并计了一层，进一步判断是否到达目标层数，到达则起爆，否则回到步骤3)。

3 算法仿真实验

为了进一步验证包络预测的动态阈值算法的准确性，本文采用一组数值仿真得到的侵彻多层靶过载信号数据进行验证。仿真结构参数与工况如下：弹体长度为1.08 m，弹径为196 mm，采用G50材料的截卵形弹体以1 200 m/s的初速连续侵彻70 mm厚922A钢板，20 mm厚921A钢板，7 mm厚923A钢板，7 mm厚923A钢板，7 mm厚923A钢板，钢板之间间距为3 m，尺寸为2 500 mm*2 000 mm，仿真过载信号如图4(a)所示。包络检测算法的仿真验证如图4(b)所示，图中虚线即为拟合的包络线，实线为包络线加上相对阈值后的动态阈值线。从图4(c)中可知：该算法可以准确识别穿靶层数为5层，与实际情况相符。验证了算法的准确性。为了与固定阈值加时间窗算法进行比较，本文选取小阈值(5 000 g)和大阈值(15 000 g)两种情况分别分析。当阈值取较低值时，固定阈值加时间窗算法识别出穿层数为9层，其远大于实际层数，导致多计层，如图5所示。当阈值逐渐增大到刚好排除掉非穿层信号时，又会漏掉第三层靶的计数，导致漏计层，如图6所示。

图4 采用包络预测的动态阈值算法的仿真曲线

图5 采用较低阈值的固定阈值加时间窗算法的仿真曲线

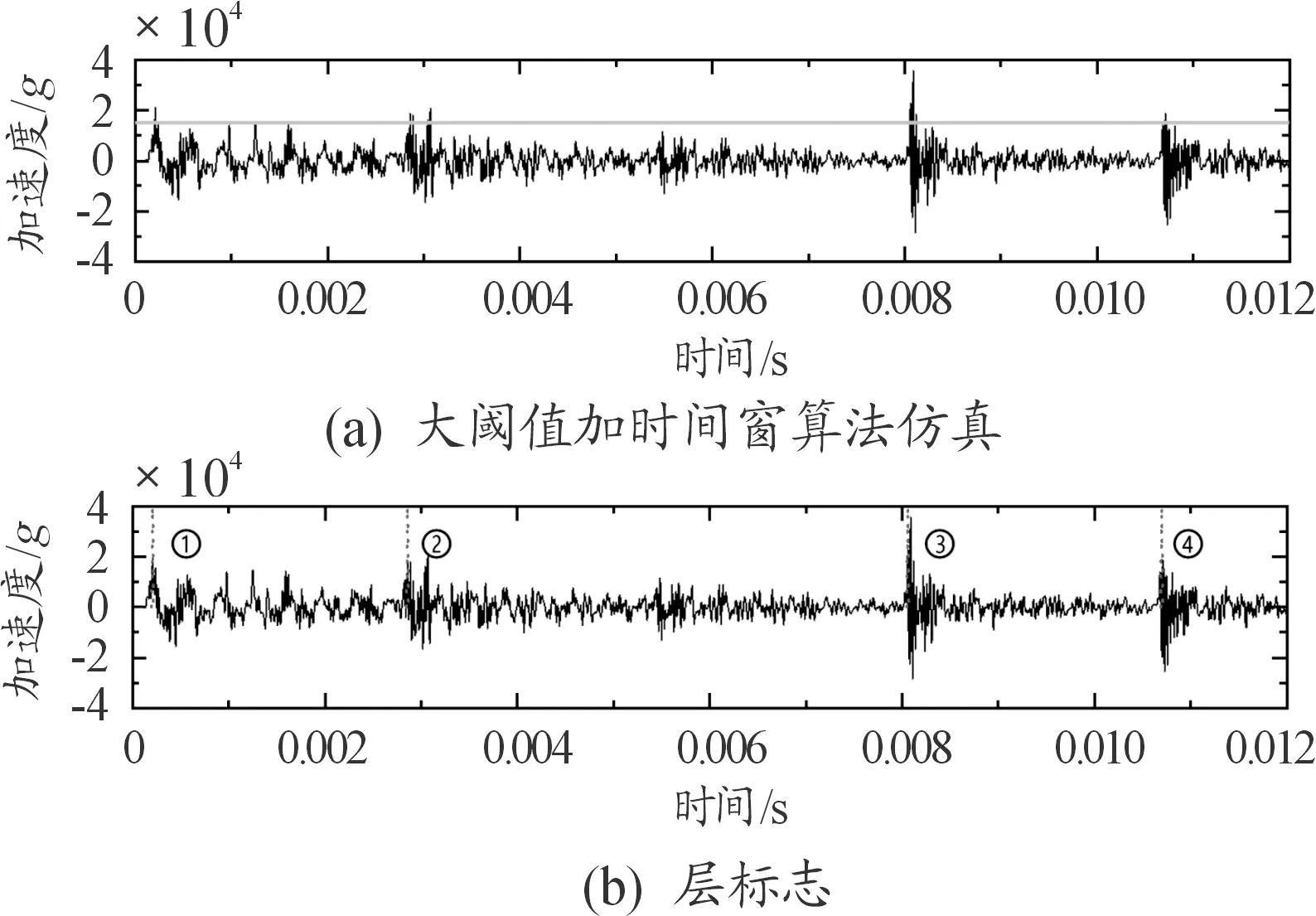
图6 采用较高阈值的固定阈值加时间窗算法的仿真曲线

通过上述分析可以看出：当某些未充分衰减的信号大于穿层信号时，固定阈值法即使通过调整阈值也无法准确计层，而基于包络预测的动态阈值算法可以克服这一缺陷。

4 结论

本文提出的基于包络预测的动态阈值计层算法，在数据处理方面选取多组数据可较为准确提取包络线，在包络线上附加相对阈值得到的动态阈值可消除未充分衰减信号的干扰。仿真结果表明：相比于传统的固定阈值加时间窗计层算法，包络预测的动态阈值算法可以完成准确计层，验证了该方法在处理信号粘连与混叠现象时的可行性。为多层侵彻计层方法的研究提供参考。