关于带电粒子在电场中运动的题型分析


摘要:带电粒子在不同的电场中,可以有不同的运动形式,而不同的运动形式对应的处理方法也有所不同,这就要求学生在处理这类问题要有足够的运动模型储备,还要有较强的分析处理问题能力。这也是笔者认为带电粒子在电场中运动问题在试题中经常出现的原因。笔者在此归纳出带电粒子在电场运动的题型以及对应处理方法,有助于学生对运动模型的总结,培养学生概括和总结的能力。
关键词:带电粒子,直线运动,曲线运动,归纳总结
引言:带电粒子在电场中运动无论在人教版老教材还是新教材中都是单独一节内容,教材中都是介绍带电粒子在匀强电场中直线加速和偏转两种问题。在学习静电场以前,学生基本上已经学习了高中范围内的绝大部分运动形式,但对于学生而言缺少对带电粒子在电场力作用下运动的归纳和总结,笔者根据学生的学习规律和知识接受情况,特总结出了带电粒子在电场中运动的模型以及处理方法。希望能够帮助学生整体上认识带电粒子的运动,在脑海中建立起物理概念和物理方法的框架,从而更好的为学生服务。
一、带电粒子在电场中直线运动问题
1.匀速直线运动
带电粒子在电场中匀速运动,应抓住匀速运动受力平衡特点,对带电粒子受力分析处理相关问题。
2.匀变速直线运动
带电粒子在电场中匀变速直线运动,根据受力条件,其所受合力恒定,且合力方向必与运动方向共线,判断受力情况,可根据运动学公式或功能关系分析运动过程
如图2,电子仅在电场力由静止释放,极板电压为U,电子电荷量为e,质量为m,求经过加速后到达右极板速度。
如图6.1,电子在交变电场中做直线运动,假设极板间距足够大。由于电压周期性变化,导致电场力和加速度也周期性变化,电子做变加速直线运动。此类问题处理方法,一般可根据出发的时刻做出电子对应的v-t图像,然后根据v-t图像分析粒子运动过程,一般不同时刻出发的粒子可根据t=0时刻图像平移可获得。这里可以用另外一个小技巧做v-t图,如图5所示,已经做出电子从t=0,时刻出发的v-t图像(以向左为正方向),如图所示。这里可以将时刻共用了0时刻的图像,只用将坐标原点移至时刻,通过这个小技巧笔者认为移动坐标原点比移动图像更简洁方便,于是可根据图像中相关信息求出粒子位移等。
二、带电粒子在电场中曲线运动问题
1.匀变速曲线运动
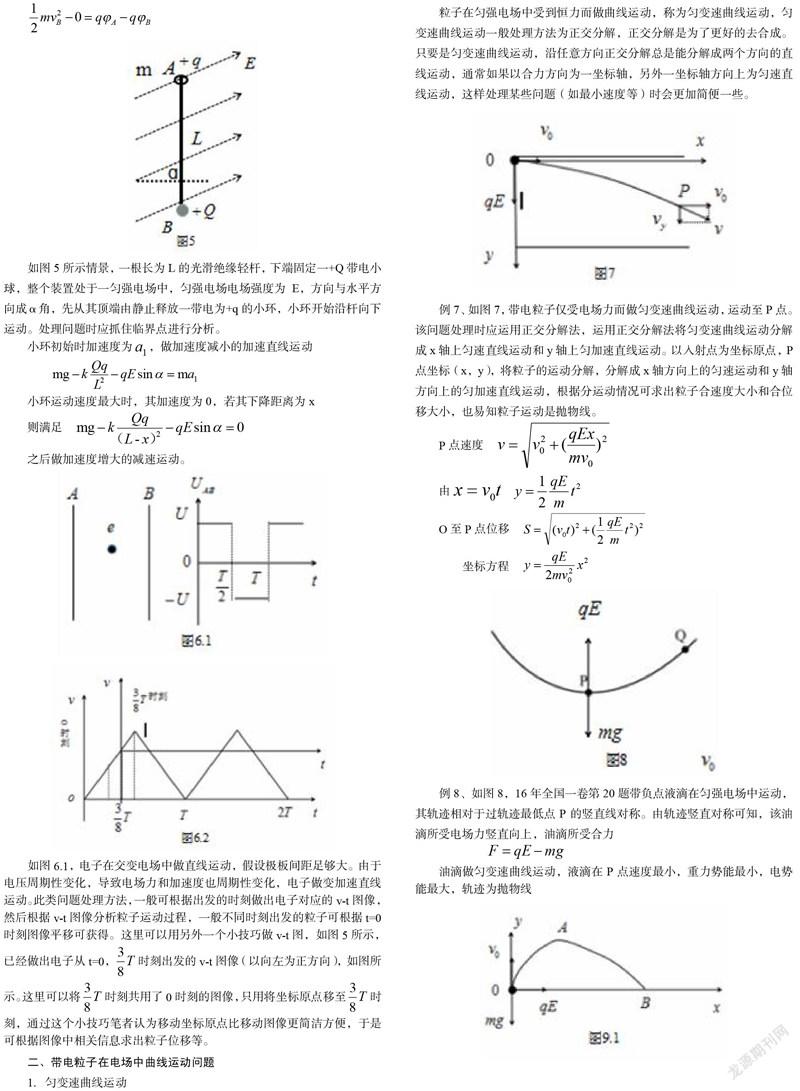
粒子在匀强电场中受到恒力而做曲线运动,称为匀变速曲线运动,匀变速曲线运动一般处理方法为正交分解,正交分解是为了更好的去合成。只要是匀变速曲线运动,沿任意方向正交分解总是能分解成两个方向的直线运动,通常如果以合力方向为一坐标轴,另外一坐标轴方向上为匀速直线运动,这样处理某些问题(如最小速度等)时会更加简便一些。
例7、如图7,带电粒子仅受电场力而做匀变速曲线运动,运动至P点。该问题处理时应运用正交分解法,运用正交分解法将匀变速曲线运动分解成x轴上匀速直线运动和y轴上匀加速直线运动。以入射点为坐标原点,P点坐标(x,y),将粒子的运动分解,分解成x轴方向上的匀速运动和y轴方向上的匀加速直线运动,根据分运动情况可求出粒子合速度大小和合位移大小,也易知粒子运动是抛物线。
例9、如图9.1所示,带电为+q,质量为m的油滴以速度竖直向上射出,空间内同时存在水平向右的匀强电场E。带电油滴由于受重力和水平向右恒定电场力作用,所以油滴做匀变速曲线运动。此时通常可以按两种方法正交分解,其一,不分解初速度,将运动分解为水平方向初速度为0,加速度为的匀加速直线运动,和竖直方向初速度为向上,加速度为的竖直上抛运动。其二可按照图9.2,将重力和电场力等效为一个力,即合力,不分解合力,分解初速度。将运动分解至沿合力方向和垂直于合力方向,y方向上为初速度加速度的匀变速直线运动和x方向上为匀速运动。
如图10.1所示,带电为+q,质量为m(重力不计)的带电粒子以垂直于电场方向射入两极板,两极板从粒子进入开始时立即加上交变电压。由于粒子只受电场力,而电场力是周期性变化的,故粒子做变加速曲线运动。但就每半个周期而言电场加速度不变,故此类问题处理方法仍跟匀变速曲线运动处理方法一致,可将运动正交分解至沿初速度方向和垂直于初速度方向。x軸方向匀速直线运动,y轴方向做周期性变加速直线运动,为了求出粒子的合运动,可分别做出两个方向上的v-t图像。如图10.2所示。
2.圆周运动
粒子受电场力而做圆周运动,应对带电粒子受力分析,将粒子受力沿圆轨迹半径方向和圆切线方向分解,沿半径方向为向心力,沿切线方向为切向力。特别的匀速圆周运动无切向合力,合力等于向心力。变速圆周运动类单摆模型,两侧最高点向心力为0,合力等于切向力。向心力只改版速度方向,切向力只改变速度大小。再结合功能关系可解决圆周运动的一般问题。
例11、如图11所示,是粒子只受静电力作用下做匀速圆周运动的情景,处理此类问题关键是把握住向心力的来源问题。其中甲是点电荷+q在绕孤立场源电荷做匀速圆周运动,由点电荷所受库仑力充当向心力;图乙中是点电荷+q在两个等量-Q电荷连线的中垂面上做匀速圆周运动,由点电荷所受的两个库仑力的合力充当向心力。
例12、如图12所示,带电为+q质量为m的带电小球在半径为R的光滑圆轨道内侧运动,整个平面内存在水平向右电场E,此时小球在竖直平面内做变速圆周运动。该类问题往往考查小球在圆周内通过的情况。此类问题应找到等效场最高点。如图乙,可假设小球置于圆心处,小球在电场力和重力作用下必定会朝等效最低N点做“落体”运动,故N点过圆心反向延长与圆轨道交点M为等效最高点。带电小球在圆周运动过程中在N点速度最大,在M处速度最小。与MN垂直过圆心的直径PQ两侧为等效水平端点,小球可在PQ之间做类单摆运动。
过B点时速度应满足:
过C点时速度应满足:
而过D点必须先满足过等效最高点M点,过M点需满足:
总结:总之,带电粒子在电场中的运动是多种多样的,也可以是多种运动形式的组合,这也顺应着物理课程的大单元教学,也是培养学生物理核心素养良好体现。教学中应关键抓住带电粒子的受力特点,分析其运动特点,采取相对应的处理方法解决问题。
参考文献:
[1]王美芳. 高中“带电粒子在电磁场中的运动”相关问题的研究[D].苏州大学,2016.68.
[2]王振虎.带电粒子在电磁场中运动轨迹赏析[J].高中数理化,2015(02):26-27.
作者简介:甘夏贤(1989-),男,汉族,安徽潜山人,本科,中学教师,研究方向:物理教学。

