中国科技进步贡献率测度——基于OECD《生产率测算手册》非参数法

（中国社会科学院人口与劳动经济研究所，北京 100028）

中国十分重视科学技术工作，研发投入资金连年增长，2019 年达到21 737 亿元（约合3 151 亿美元），研发投入强度达到2.19%［1］。与2000 年相比较，研发投入总规模增长了23 倍，研发投入强度提高了1.3 个百分点。科技产出成果显著，2019 年境内外专利申请量达到438 万件，授予专利权259.2 万件，特别是通过世界知识产权组织的《专利合作条约》(PCT)体系，提交了约5.9 万件申请，首次成为专利申请量最多的国家［2］。因此，中国大规模研发经费投入有效地促进了科学技术进步，而这种进步对经济增长产生了十分显著的影响，通常使用科技进步贡献率来表达。长期以来，我们党非常注重经济增长中科技进步的份额，比如，党的十四大报告提出，要“努力提高科技进步在经济增长中所占的含量，促进整个经济由粗放经营向集约经营转变”［3］。我们理解，这个含量就是科技进步对经济增长的贡献。那么，如何来科学测度这项指标，一直是国内外学者探索的热点课题。

1 研究综述

国外相关研究认为，所谓科技进步贡献率，其实质就是经济增长最终成果中，科技进步所贡献的份额，往往被视为全要素生产率。从上世纪30 年代开始，美国数学家柯布和经济学家道格拉斯联合提出的生产函数（简称“C-D 函数”）一般形式，成为揭示经济投入与产出关系的经典工具，也是测度科技进步贡献率的原始模型［4］。到40 年代，荷兰经济学家丁伯根正是在C-D 函数基础上，在物质资本、劳动力两个投入要素中加入时间要素，从而创造了表达经济效率的方式，也是第一次提出全要素生产率概念，并将其视为广义的技术进步，从而出现了定量测度科技进步贡献率的可能［5］。到50 年代，美国经济学者索洛对经济产出中技术进步的作用进行专门研究，将产出中除物质资本、人力资本以外的部分称之为“剩余”，这部分无法得到明确解释，把其全部归结为因科技进步引起的经济增长部分，这就是著名的“索洛剩余”［6］，成为测度科技进步贡献率的主流方法。

从国内来讲，科技进步贡献率研究工作一直是在政府部门主导下进行。上世纪80 年代初期，中央政府在制定“六五”计划时，就已经将经济增长中科技进步作用纳入指标设计，在借鉴国际经验基础上，率先对工业领域的技术进步作用进行研究，这算是开启了国内研究科技进步贡献率的先河。这个时期部分学者就简化科技进步贡献率测算工作进行了深入研究，比如万伟勋［7］、狄昂照［8］学者。90年代初期，中央有关部门通过下发文件方式，要求地方部门定量开展科技进步的贡献测度工作，并逐步将其纳入国民经济评价指标体系加以考核［9］。这个时期我国科技进步贡献率测算工作蓬勃发展，在理论研究、方法创新上都取得大量突破，具有代表性的有冯英浚等［10］、朱希刚等［11］、郭学理［12］、杜希双［13］。进入新世纪后，我国制定的2006—2020 年期间中长期科技发展规划，明确提出到2020年科技进步贡献率达到60%的目标［14］。2016 年党中央、国务院印发的《国家创新驱动发展战略纲要》又提出，到2020 年我国进入创新型国家行列，标志之一就是科技进步贡献率要达到60%以上［15］。这一时期科技进步贡献率研究更多是用于指导实践，特别是在制定国家科技战略方面该指标应用广泛，主要代表有傅毓维等［16］、邓国华［17］、魏和清［18］、于洁等［19］。

以上这些事例表明，研究科技进步贡献率已经成为我国科技部门主要工作内容之一，特别是最近几年，科技部门一直在探索如何科学测度科技进步贡献率的相关工作，2016 年还专门组织编写了《科技进步贡献率测算手册》，其目的就是要在我国建立该指标的测算规范。同时，在政府部门引导下，国内学术界对科技进步贡献率的研究一直热度不减，且取得了丰硕的研究成果。检索《中国知网》后发现，截至今年5 月初，各类学术期刊论文标题中含“科技进步贡献率”的高达470 余篇，这些论文时间跨度从1993 年到2020 年，其中，中文核心期刊有140余篇，CSSCI 期刊有70 余篇。我们分析这些文献后发现，测度科技进步贡献率最关键、最困难的工作是科学估算要素产出弹性，只要解决好要素产出弹性估算问题，科技进步贡献率测算工作就迎刃而解。大部分做法是，以C-D 函数为基础，结合研究需要来改进回归模型，从而测算出要素产出弹性。我们发现，使用回归模型测算科技进步贡献率有很多缺陷，主要表现在该模型对时序数据要求十分严格，既要时间足够长，还要求数据值不能波动太大，否则测算结果很不稳定，突出表现在不同学者即使采用同样模型、同样时序数据，其测算结果也会有很大差异。部分学者对这一现象进行了批评，认为当前国内学术界测度科技进步贡献率有一不良现象，就是滥用、乱用数学模型突出，很多使用简单方法即可完成的研究，非要将简单问题复杂化，过度使用数学模型和假设检验，部分甚至将研究问题变成了演算数学习题［20］。为简化科技进步贡献率测算工作，OECD 在长期研究积累基础上，2001 年编制了《生产率测算手册》［21］，给出国际公认的要素贡献测算范围和方法，并在应用中收到了不错效果。因此，在本研究中，我们试图借鉴其方法来测算中国科技进步贡献率。

2 《生产率测算手册》简述

《生产率测算手册》指出，研究生产率的主要有学术界和政府部门两个主体，二者在研究方法选择上差异较大。对于学者来讲，其关注重点往往聚焦在方法的前沿性，研究结果一般都是一次性的，大部分并不关注成果的后续应用。学术界研究生产率将经济计量方法即参数法作为常用工具，这种方法增加了问题的复杂性，所需数据量特别大，且一旦数据更新时，需要对所有参数重新进行估计，从而降低了测算结果的即时性，得出的结果也忽高忽低，很不稳定，容易引起质疑。对于政府部门来讲，往往要将其研究结果定期面向公众发布，要求结果保持稳定性和连贯性，甚至还要用于比较孰优孰劣等问题。所以，《生产率测算手册》认为，由于政府部门需要定期开展生产率测算工作，强烈建议使用非参数方法。这种方法将经济理论与指数理论有机融合，为我们提供新的测算思路，也提供了一种更加便捷、更为有效的测算方法，是简化研究问题的典范。同时，《生产率测算手册》着重指出，测算生产率思路的实现，不但要考虑数据的可获得性，而且也要考虑获取数据的成本。当前，国际上主流趋势是，只要能对生产率测算结果给出合理解释，就可以采用不完全符合理论标准的方法与工具。对于非参数方法来讲，正符合这一要求，它的主要优势在于，可以固定地、持续地对生产率进行测算。在本研究中，我们讨论的对象是，经济产出中除物质资本、人力资本以外的要素对经济增长的贡献，也即广义的科技进步，与《生产率测算手册》的研究对象类似，故借鉴其方法具有一定可行性。

3 测算思路

测度科技进步贡献率，比较主流的思路是，将模型中要素产出弹性估算出来，使用增长方程计算出要素贡献率，往往注重计算出科技进步贡献率的绝对数值。但是，《生产率测算手册》则是以要素指数为基础，采用指数化形式来表达科技进步的贡献程度，并不是绝对数值。具体做法上，《生产率测算手册》引入了Divisia 和Tornqvist 两个经典指数，使用Divisia 指数将影响产出结果的因素加以分解，从而得到测算要素贡献率的模型。由于该模型仍然是以“索洛剩余”为基础，且属于连续函数，特别是在少量数据条件下与实际生产并不相符，所以使用Tornqvist 指数进行逼近，得到计算要素贡献率的离散模型，从而达到直接测算要素贡献率目的。同时，Tornqvist 指数还有一好处，就是可以实现局部与总量之间的关联测算，比如，在测算我国各省份的科技进步贡献率后，通过汇总方式实现国家层面的科技进步贡献率，这种优势是传统回归模型不具备的。由于《生产率测算手册》将科技进步贡献率Divisia 指数到Tornqvist 指数的整个推导过程已经做了充分交代，我这里就不再做重复工作，直接使用指数模型，直接给出计算我国各省份科技进步贡献率的Tornqvist 指数模型，并将汇总模型一并展示。

3.1 省级层面科技进步贡献率Tornqvist 指数模型

3.2 科技进步贡献指数汇总模型

从国内众多研究成果看，大部分侧重对某一地区或产业的科技进步贡献率进行测算。《生产率测算手册》认为，应当将地区、产业层面与总量联系起来，进行二者之间的关联测算。实际上，就是通过科技进步贡献率测算，建立起微观、中观和宏观层面之间的经济联系，可以体现地区或产业对总量的实际贡献，总量的变化通过地区或产业层面得到解释，还有利于将研究成果转化为政府决策。

在我们测算出我国各省份的科技进步贡献指数后，通过如下汇总模型，可以计算出国家层面的科技进步贡献指数。我们以每个省份GDP 所占比例作为汇总权重，汇总模型为：

3.3 要素份额α、β 的估算

当我们完成α、β估算后，就可以求出科技进步贡献率指数。

《生产率测算手册》指出，生产函数产出部分Y，可以使用增加值来表示，且采用要素收入法核算，即由劳动者报酬、固定资产折旧、生产税净额以及营业盈余等四个部分构成。其中，劳动者报酬反映劳动服务量，固定资产折旧额反映资本服务量；也可把劳动者报酬视为劳动产生的收入，而固定资产折旧、营业盈余则是资本产生的收入。因此，人力资本影响经济增长的权重β可以用以下公式测算：

权重α、β取值是基期和报告期的均值，即：

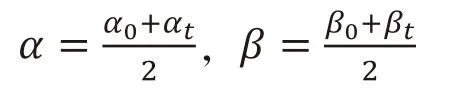
这样，就可以直接计算出科技进步贡献指数，江兵等［22］使用这种方法测算科技进步贡献率，得到了理想的结果。

4 数据处理

测算科技进步贡献率，很有必要将数据选择与处理过程交代清楚。从前面众多文献看，很多学者宁愿在模型推导下足了功夫，而对数据如何选择、如何处理交代很少，部分甚至只字不提，仿佛这些工作并不重要。实际上，从目前国内统计刊物所提供的数据看，很难找到同一口径的经济产出、物质资本以及人力资本现成数据直接用于测算，这就需要我们加以推导才能获得。所以，对于一篇负责任的论文来讲，必须要告知读者数据处理过程［23］。

从前面模型可知，测算科技进步贡献率需要经济产出、物质资本、人力资本三类数据。对经济产出来讲，我们需要使用收入法计算的地区生产总值数据。但就国家层面看，国家统计局公布的地区生产总值数据是按支出法计算的，没有按收入法计算的GDP 数据。值得庆幸的是，统计局公布了我国31个省份（其中不包含香港特别行政区，澳门特别行政区以及中国台湾地区）按收入法计算的数据。所以，我们先对我国各省份的科技进步贡献率测算出来，然后再依据《生产率测算手册》提供的方法，汇总得到国家层面的科技进步贡献率。考虑到各省市收入法地区生产总值数据公布到2017 年，所以，我们测算科技进步贡献率时，数据期间选择最近10 年，即2007 至2017 年，并将2007 年作为唯一基期年份。具体如下：

4.1 估算要素产出弹性有关数据

使用我国各省份2007—2017 年期间按收入法计算的当年价GDP 来表示劳动者报酬、固定资产折旧、生产税净额及营业盈余之和，每年份各省市劳动者报酬作分子，从而计算出人力资本对产出的权重β，并通过α=1-β计算出物质资本对产出的权重α值。为节约篇幅，我们在下面只是给出人力资本对产出的权重β 均值计算结果，见表1。

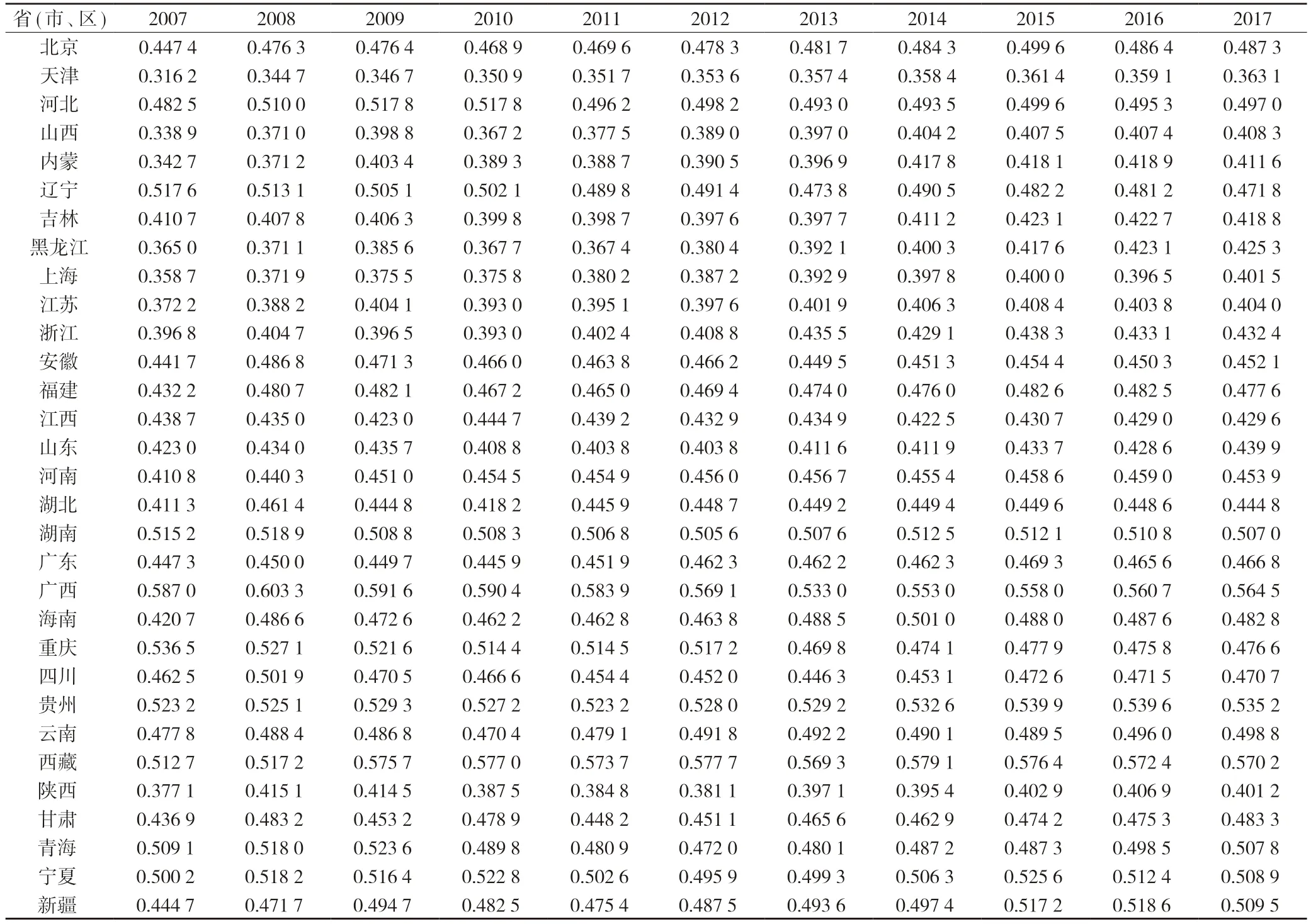
表1 我国各省份人力资本对产出的权重均值

4.2 经济发展指数

《生产率测算手册》指出，当选择增加值（国家或省市层面称为地区生产总值）代表经济产出时，只需考虑初始物质资本、人力资本投入等要素，不用考虑中间产品投入。为简便起见，我们选择2007—2017 年期间各省市地区生产总值作为产出，以此来计算经济发展指数。从各省市统计年鉴可以得到地区生产总值指数后，以2007 为基期，计算出各省市年度经济发展指数，见表2。

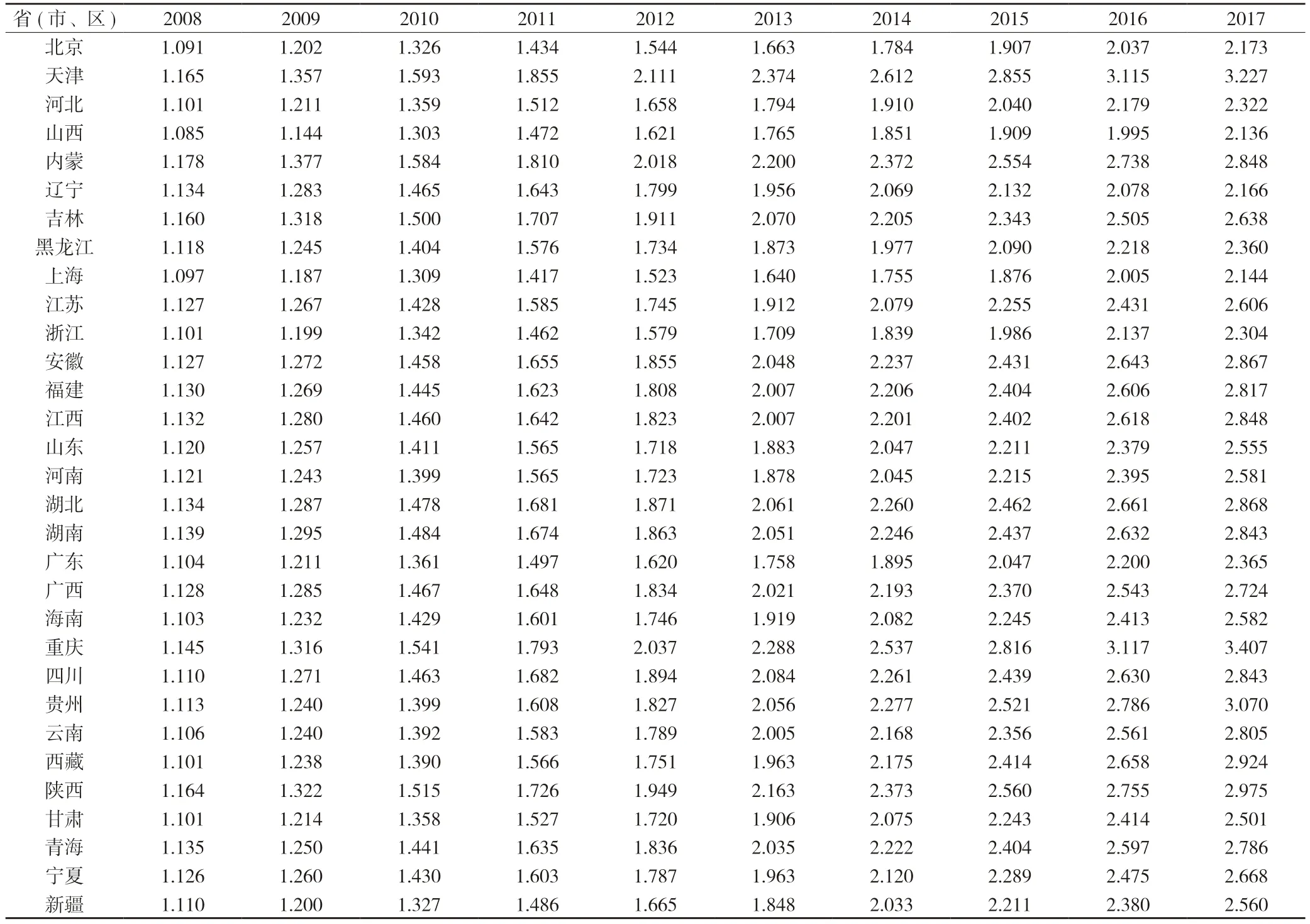
表2 我国各省份经济发展指数

4.3 物质资本存量指数

《生产率测算手册》用了大量篇幅来讨论物质资本K 的有关问题。我们将各省市按支出法计算地区生产总值中固定资本形成额分离出来，作为计算物质资本K 的原始数据。一般认为，对一个地区经济增长作出贡献的不仅是当年新投入使用的固定资本，而且包括以前投入并发挥作用的部分。所以，计算物质资本时，主要是看当年存量而不是增量，并将物质资本存量加以缩减，得到不变价物质资本存量数据。为得到我国各省份2007—2017 年期间的物质资本存量，本文具体做法是，使用1978 年固定资本形成总额除以10%得到各省份初始资本存量，固定资本折旧率按9.6%计算，这样就计算出每年分各地区不变价物质资本存量K，进一步计算出以2007年为基期的固定资本投资存量指数，结果见表3。

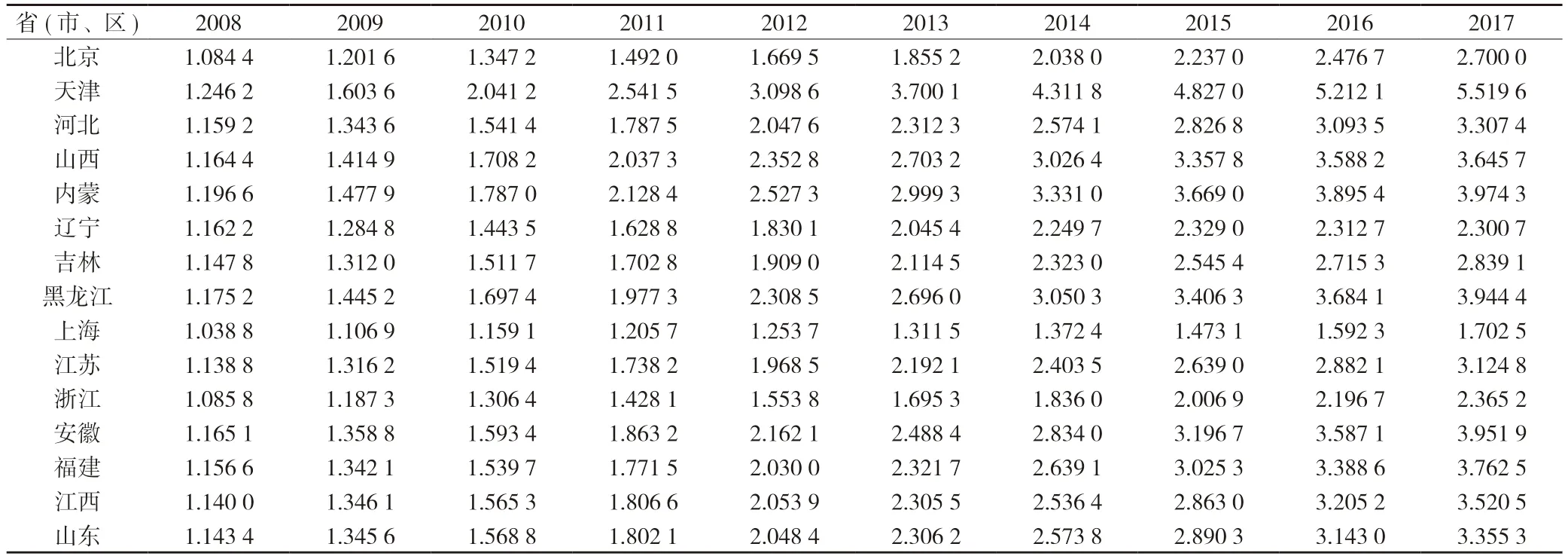
表3 我国各省份固定资本存量指数

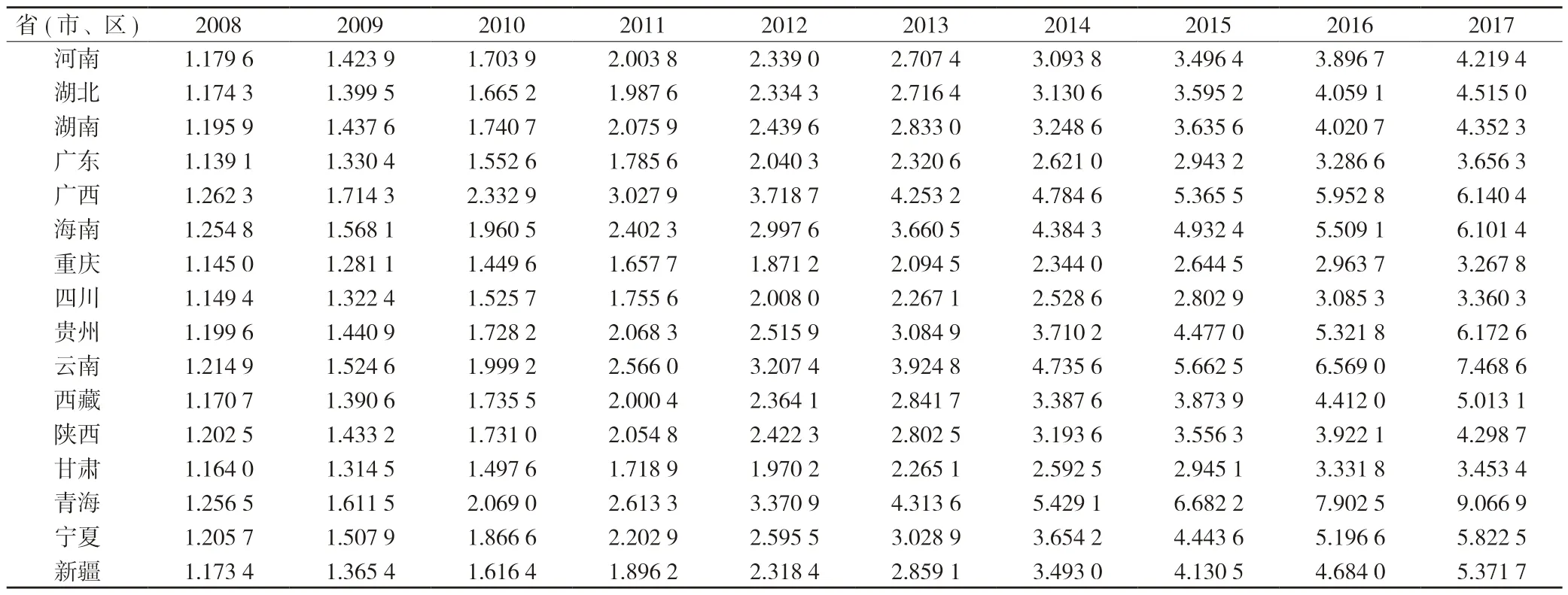
表3 （续）

4.4 人力资本指数

对于人力资本投入数据，《生产率测算手册》做了非常细致的讨论，认为生产过程中最重要的因素就是人力资本，选择不同标准，对生产率测算结果会产生显著影响。人力资本投入可以是总工时数、全职就业人员当量、就业人员数量等三种标准，由于存在兼职、加班、旷工以及轮班等情况，简单使用就业人员数量无法真正反映生产中人力资本投入实际情况，《生产率测算手册》认为，使用总工时数计算人力资本投入是最佳的，不过，如何获取统计资料来保持工时数的完整性和质量，这是实际研究中面临的难题。从国内众多研究来看，很多学者使用就业人数来表示人力资本投入，我们认为，从业人员人数无法反映人力资本质量差异，不是衡量人力资本的最优数据。我们采用从业人员受教育年限来代表人力资本，这既反映了不同时期人力资本数量差异，也反映了质量差异，还可用于国际比较。具体做法是，借鉴美国经济学者麦迪生（Maddison）［24］初等教育等量年标准，以接受初等教育水平为基础（即定系数为1），1 个中等教育年、高等教育年分别是初等教育年的1.4 倍和2 倍，这个倍数主要表达的是，受过不同教育程度从业人员，他们从事生产活动时获取知识方面的能力差别。我国受教育程度分为7 类，分别是未上过学、小学、初中、高中、大专、本科、研究生及以上，我们将教育当量设定为：未上过学、小学教育当量为1，初中、高中为1.4，大专及以上为2；每个阶段接受教育年限标准，我们借鉴2010 年中央组织部制定国家中长期人才发展规划纲要时的做法，未上过学1.5 年，小学6 年、初中9 年、高中12 年、大专15 年、本科16 年、研究生（包括硕士和博士）平均为19.6 年，这样，就形成了计算从业人员受教育年限的标准［25］。从历年《中国劳动统计年鉴》中，可以得到从业人员受7 种教育程度的比例，从而可以计算出我国各省份2007—2017 年期间从业人员受教育年限，进一步测算出以2007 年为基期的人力资本指数，详见表4。

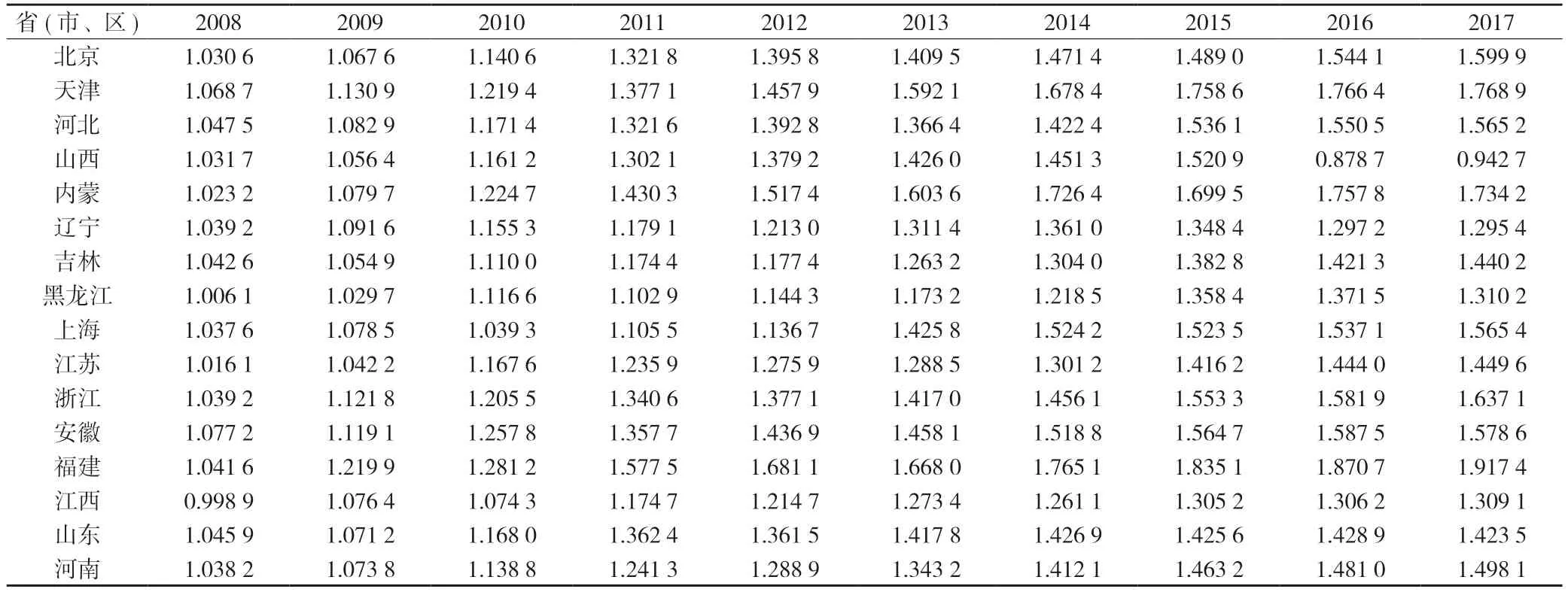
表4 我国各省份人力资本指数

表4 （续）

5 测算结果及分析

5.1 我国各省份科技进步贡献指数

将以上数据代入省市层面科技进步贡献Tornqvist 指数模型，可以计算出各省市的科技进步贡献指数，结果见表5。

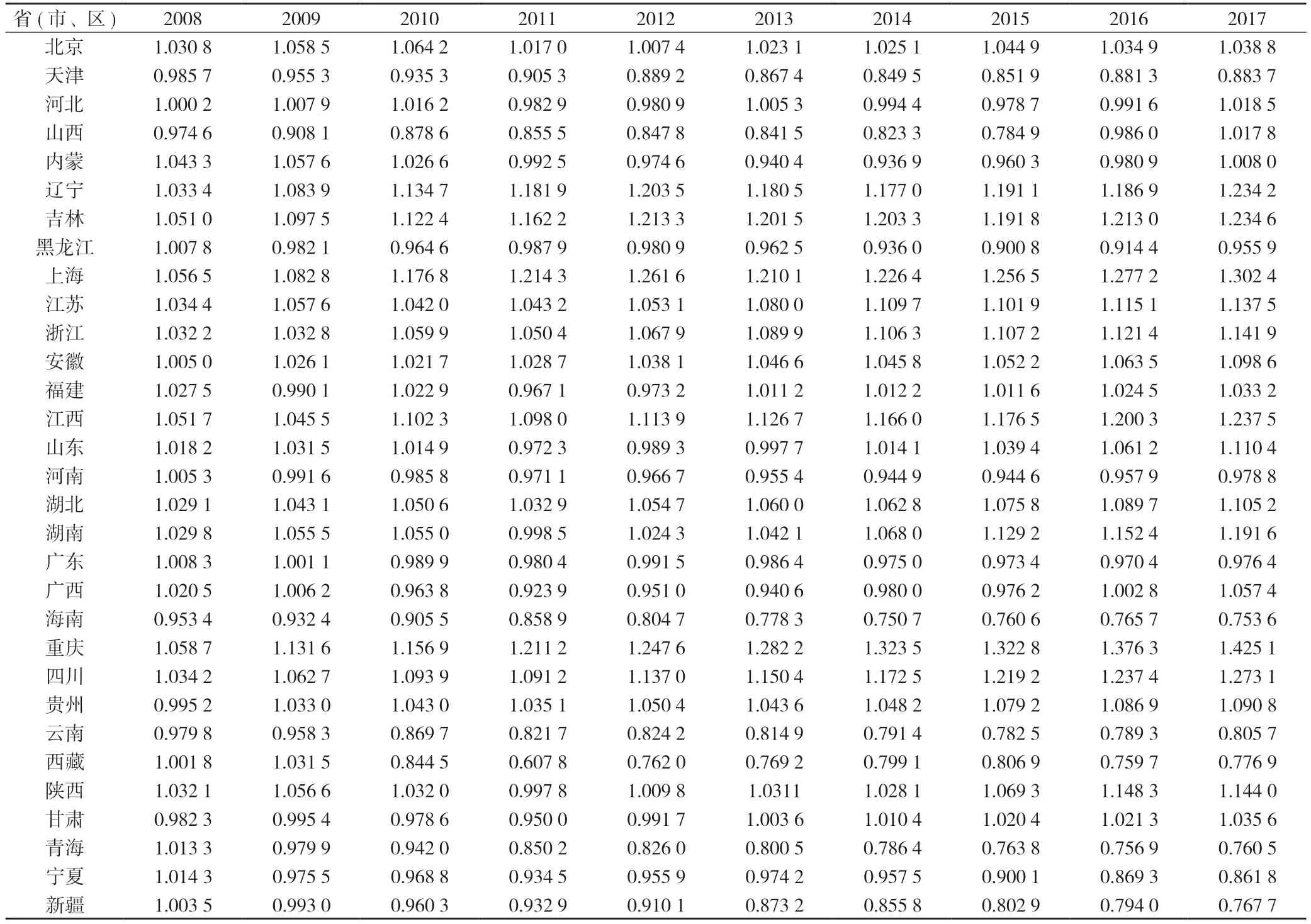
表5 我国各省份科技进步贡献指数

5.2 科技进步贡献指数汇总

5.2.1 汇总平均权重

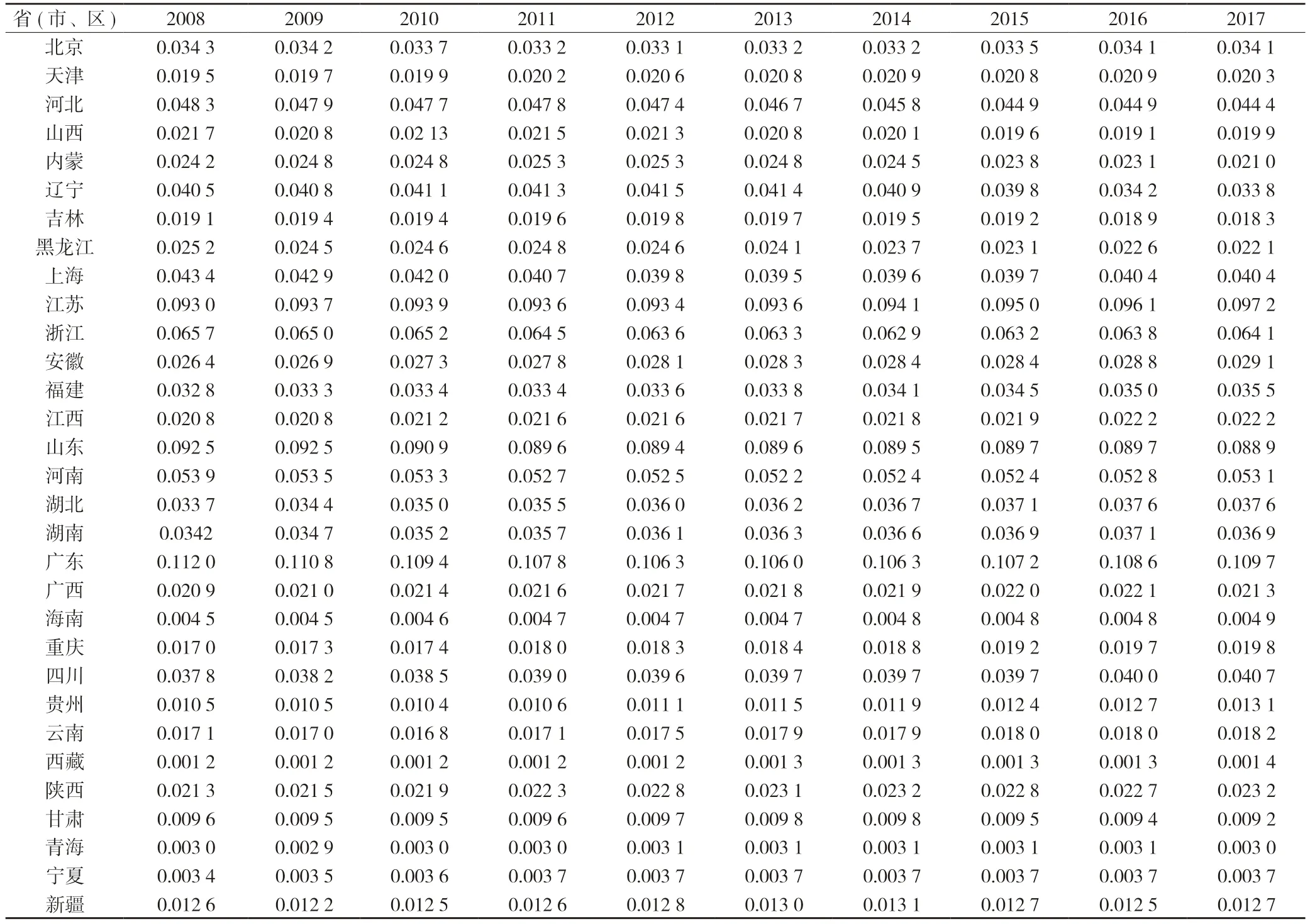
表6 我国各省份GDP 所占比例均值

5.2.2 中国科技进步贡献Tornqvist 指数

根据科技进步贡献汇总模型，可以计算出国家层面的科技进步贡献指数，详见表7。

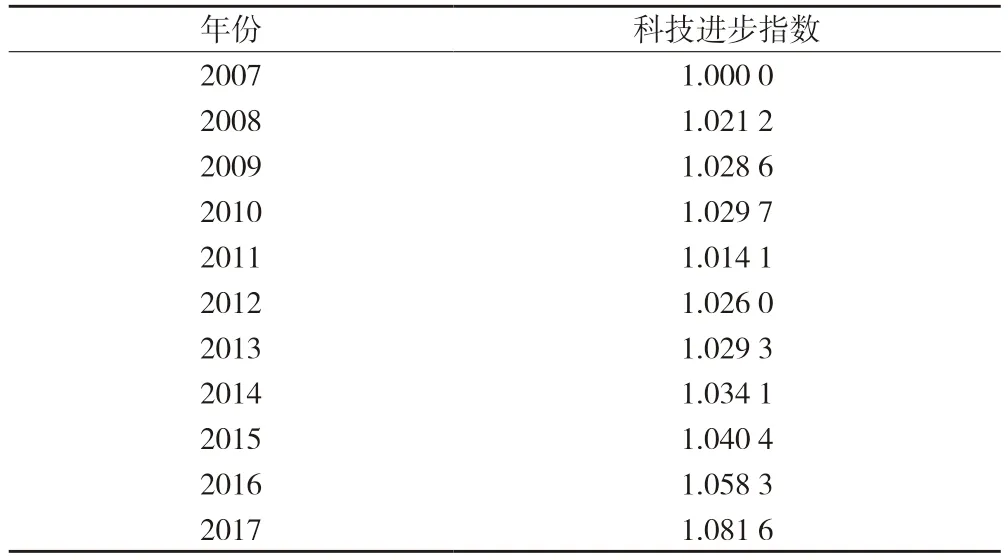
表7 我国科技进步贡献指数

根据表7，我们可以这么认为，当指数大于1 时，说明科技进步贡献率是提高的，反之，当小于1 时，说明是降低的。这种科技进步贡献率表达方式，比索洛余值更为直观和明确，不容易引起认识上的偏差。同时，从汇总模型可以看出，如果要得到每个年份的科技进步贡献率绝对数据，只要我们科学测算出基期年份的科技进步贡献率，以后年份就可以通过指数来表达，并以此为基础，直接计算出以后各个年份的科技进步贡献率数据，这样大大降低了科技进步贡献率的测算工作量，为及时发布年度数据提供了充分保障。

《中国科技统计年鉴（2019）》显示，2003—2007 年期间中国科技进步贡献率已经达到46%，我们以此为基础，结合2008—2017年科技进步贡献指数，得到各个年份的科技进步贡献率绝对数据，见表8。

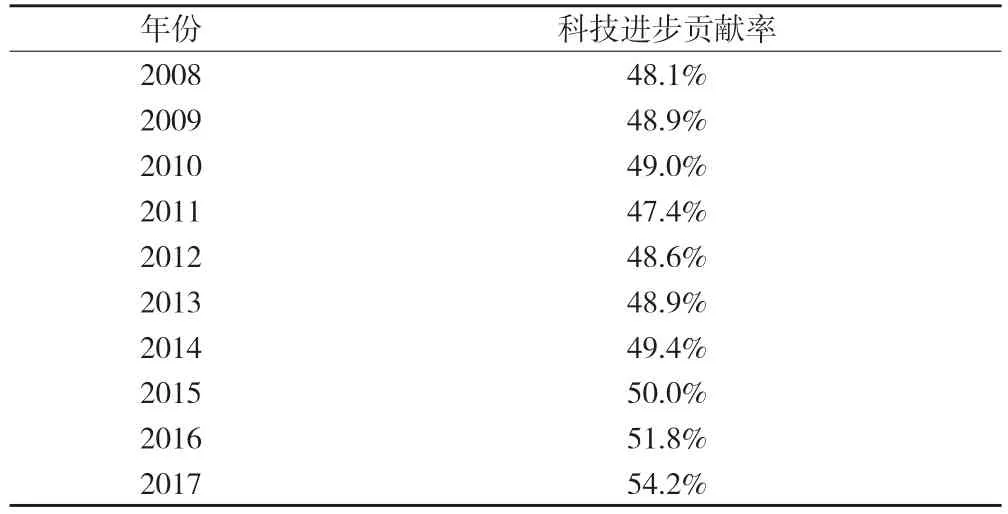
表8 2008—2017 年中国科技进步贡献率

从测算结果看，在2007 至2017 年期间，中国科技进步提高了8.2 个百分点，达到了54.2%。

6 结论

科技进步贡献率已经是一个被公认的概念，具有其严密的内在逻辑及明确的内涵界定，也有其基本的理论基础和测算方法，我们需要在一个统一框架下来测算和运用，切不可按照自己的直观理解去随意解读和使用。因为从不同层面来讲，科技进步贡献率的内涵不同，比如，从微观层面来讲，科技进步主要与企业拥有的人才素质、设备质量、工艺流程、管理经验等密切相关；从宏观层面来看，一个地区、行业或国家的科技进步，除了包含企业层面的因素外，还跟产业布局、经济结构调整、经济制度等因素相关。同时，从横向看，不同地区科技进步贡献率相互比较没有实际意义，经济落后地区的科技进步贡献率不一定就比发达地区低，理由是科技进步贡献率是根据经济增长速度来测算的，这是一个反映科技进步动态变化的过程，表现形式是加权后的要素增长与总增长的比例。对于经济发达地区来讲，其本身的科技进步水平较高，再进一步提升空间并不大，因为这些地区就业比较充分，特别是与物质资本相比较，人力资本年均增长速度相对较低，这样人均资本就增长很快，结果是，受资本边际效益递减规律影响，产出增长往往会低于资本增长，这样往往无法达到高的科技进步贡献率水平［26］。

另外，从测算方法来看，我们借鉴OECD《生产率测算手册》介绍的非参数方法，使用指数形式来表达科技进步贡献程度，这在一定程度上简化了科技进步测算工作，特别是对于政府部门常年发布科技进步贡献率数据来讲比较实用，为规范该指标的测算提供了新的方法选择。