复数的历史与教学思考

华南师范大学(510631) 邱 勇 何小亚

1 复数发展史的概述

1.1 初露端倪

复数产生的最初缘由在于数学家们遇到了负数开平方的问题. 最早记载负数开方的文献是公元1 世纪古希腊数学家海伦所著的《度量论》,他在书中讨论了“平顶金字塔不可能问题”. 这个问题描述如下:

如图1 所示的正棱台, 上下底面分别是边长为b和a的正方形,侧棱长为c,求此时的高h?海伦推导出h可以由一个漂亮的式子给出(推导过程已由图中给出提示,感兴趣的读者可以自行尝试),即

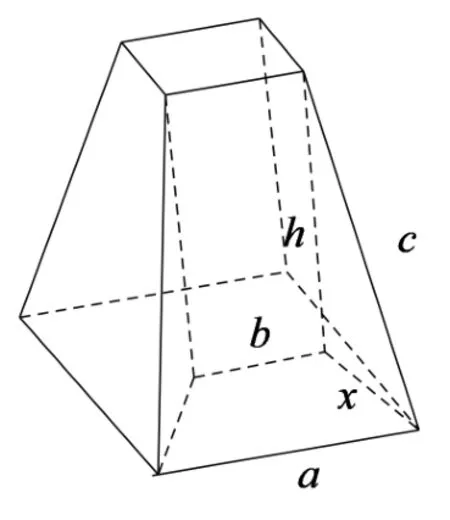
图1

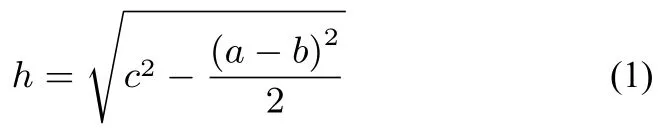
海伦还给a,b,c赋了具体的数值进行举例,如令a= 10,b=2,c=9,就可以利用公式(1)求出h的值:

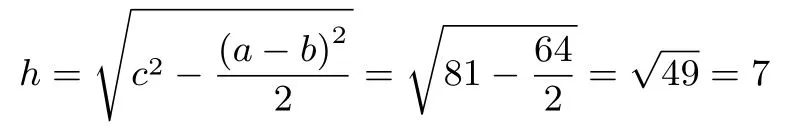
但是, 海伦随后又举了一个特殊的例子, 他令a= 28,b=4,c=15,此时继续用公式(1)计算h的值:

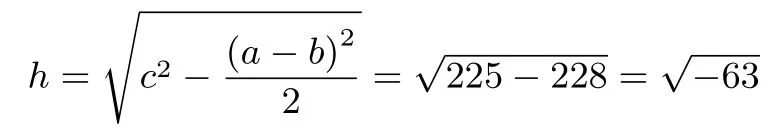
从而,海伦得到了一个不可能存在的“平顶金字塔”,对于这个结果海伦并没有过多的讨论,但这的确是数学史上首次对负数开方的记载. 不论海伦是有意还是无意地忽视这个结果,他都错过了首次发现虚数的机会.

其后,许多的数学家都遇到了类似的问题. 例如,古希腊最伟大的数学家丢番图在《算术》一书中已经遇到了“不可约”的一元二次方程336x2+24=172x. 12 世纪的印度数学家婆什伽罗也曾指出:“正数与负数的平方都是正数,正数的平方根有两个,一个正,一个负. 但是负数没有平方根,因为它不是一个平方数. ”欧洲的学者,12 世纪西班牙的巴希亚、13 世纪意大利数学家斐波那契、15 世纪意大利数学家帕西沃里和法国数学家丘凯在讨论一元二次方程的根时都遇到了的情形.

1.2 萌芽时期

如果说以上只是虚数的初露端倪,那么16 世纪意大利米兰数学家卡当算是第一个认真讨论虚数的人了. 卡当提出了这个问题: 如何把10 分成两部分,使它们的乘积为40. 这个问题的实质是解一元二次方程x(10-x) = 40,显然这是一个在实数范围内无解的方程. 但是卡当先把10 等分,得到两个5,相乘得25,减去40 得-15. 5 分别减去和加上-15的平方根就得到根为然后说“不管会受到多大的良心责备”,把相乘,得乘积为25-(-15)或即40. 于是他说,“算术就是这样神妙地搞下去的,它的目标,正如常言所说,是又精致又不中用的”.卡当包括当时的其他数学家都承认一个负数是没有平方根,所以才会如此说. 实际上,卡当还会遇到负数开放问题. 1545年通常被视为数学领域现代时期的开始, 因为就在这一年不仅三次方程、而且四次方程的解因为卡当的《大衍术》而变成了常识. 卡当在《大衍术》中用文字记载了三次方程的解法,用去了两页的篇幅(虽然这个公式可能要归功于另一名数学家塔尔塔利亚). 我们用现代的数学语言来表达方程x3+px=q的求根公式:

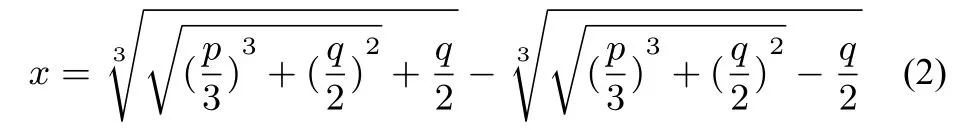
如果说在求解一元二次方程时,例如x2+2=0,x2=1,代数学家还可以说此类方程是不可解的,从而避免了对负数开方(古希腊的数学家就是这么做的). 那么,当一个三次方程的三个根都是非零实数时,公式(2)就无法避免要对负数开方了.

例如, 求解x3= 15x+4, 可得x=这种情形塔尔塔利亚称为不可约. 卡当在《大衍术》中也对方程的复数根略而不提. 复数的发展还有很长的路要走.

长久以来,数学家们产生了思维定势,认为负数开方没有意义,对虚数的研究也被搁置了. 直到20 多年后,另一位意大利数学家拉法耶尔· 邦贝利在其著作《代数》第一卷的后半部分再次对三次方程的根进行了讨论. 他发现方程x3=15x+4 有三个实数根可见4 是这个方程的唯一正根.

而运用公式(2)计算出的结果是x=+于是,邦贝利有了自己所说的“一个疯狂的想法”,仅仅在符号上不同,于是他假设:

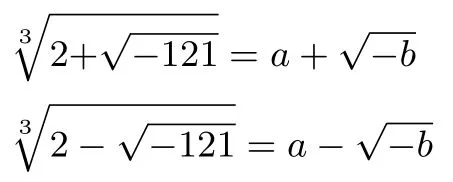
根数本身之间的关系,在很大程度上与被开方数之间的关系是一样的;我们如今说,它们是得出实数4 的共轭复数.很明显,如果实数部分之和等于4,那么,各实数部分都是2;如果一个形如的数是的立方根,那么很容易看出,b必定是1. 于是可以得到:

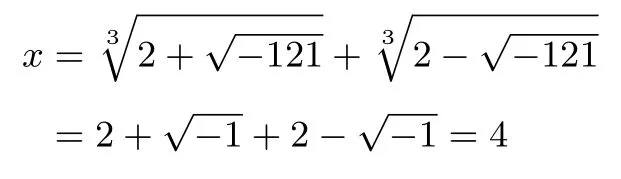
邦贝利通过他的巧妙推理,不仅让负数开方有了一定的意义而且让我们看到了共轭复数未来将起的重要作用. 不仅如此,邦贝利还用了先进的符号表示负数开方的数. 例如,他把2+3i 写为2p dim3, 2+3i 写为2m dim3. 邦贝利亦呈现了这些新数的运算法则, 用现代数学语言书写就是(bi)(ci)=-bc,(bi)(-ci)=bc,和如今是一致的.

时间来到17 世纪,虚数并没有被重视起来. 但是一直延续下来没有中断的一门研究是求解多项式方程. 早在1608年德国数学家罗特就认识到n次方程有n个根. 后来是1629年荷兰数学家阿尔伯特·吉拉德在他的著作《代数学的新发现》中给出了代数基本定理的第一个明确表述“每一个代数方程容许有同方程的次数同样多的解”,但他并没有给出证明. 正因为吉拉德有了这样的认识,他承认一个方程给定的解可能会出现不止一次,在统计解的个数时还应把虚根计入在内,即使他把虚根称为不可能的. 在他自己举例子x4+3 = 4x中,他注意到有四个根1,1,-1±面对这些不可能的解时,吉拉德直言“它们有三方面的好处: 一是因为能支持一般法则;二是因为它们有用;再者,因为除此之外再没有别的解”.至于这些不可能的解到底有什么用,吉拉德也没有说明.

另一名17 世纪的数学家笛卡尔也对解方程很感兴趣,但他更关心的是方程解的作图问题. 笛卡尔在其著作《几何学》第三卷的末尾明确地示范了一些高次方程的作图方法.尤其是三次或四次的方程, 他使用抛物线与圆相交的方法.通过几何直观来描述根时,笛卡尔意识到若圆和抛物线既不相交也不相切,这表明方程既无真(正)根也无假(负)根,此时所有的根都是虚的.他还给这些虚的根取了我们延用至今的名称“虚数”(imaginary number), 也即他认为这些数只存在于想象之中. 这从笛卡尔《方法论》中最有名的一段引言“我思故我在”可以窥见一斑,因为他只相信那些自明的观念为真.

微积分的主要奠基人莱布尼茨相对次要的贡献是对复数的研究. 1627年,莱布尼茨研究方程的解时,得到式子:

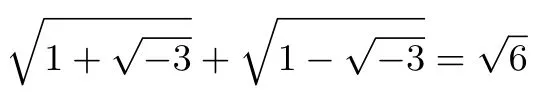
得出这令人吃惊的结果后, 莱布尼茨说到:“在一切分析中, 我从来没有见过比这更奇异、更矛盾的事实了. 我觉得自己是第一个不通过开方而将虚数形式的根化为实数值的人.”莱布尼茨写信给荷兰数学家惠更斯这一事实, 惠更斯也表示惊讶:“含有虚数的不可开根相加结果竟然就是一个实数, 这一结果令人惊讶, 前所未有. 人们绝不相信这里面隐藏着我们无法理解的东西”. 然而,莱布尼茨并没有按照标准的形式来书写复数的平方根,他也不能证明他的猜想: 若f(z)为实数多项式,则也是实数多项式. 莱布尼茨亦是一名杰出的神学家,他用一段话表明了自己的困惑:“虚数是一种两栖动物,处在存在与不存在之间,在这方面类似于基督教神学中的‘圣灵’”.

1.3 应用时期

尽管对于18 世纪的数学家来说,复数是“虚数”,方程复数根是祸根. 与复数相关的发现和应用却不断. 棣莫弗在他1730年版的《分析杂论》中,表述了下面这个公式:

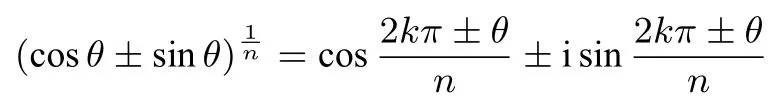
这个公式可以看作鼎鼎大名的棣莫弗公式(cosθ+i sinθ)n=cosnθ+i sinnθ的等价物.

1747年,达朗贝尔在其获奖论文《关于风的一般成因的考虑》中认为: 每一个由复数经过代数运算(包括任意次幂)建立起来的式子都是一个形为的复数. 在给出这个结论的过程时,他遇到的困难是(a+bi)g+hi的情形. 关于这个结论,还必须经过欧拉和拉格朗日以及其他人的修补.欧拉在1748年给出那个著名的关系式eiθ= cosθ+i sinθ,若令θ=π就有eiπ+1 = 0,这个关系式包含了复数系中最重要的5 个数.

欧拉与达朗贝尔因为对一些命题的兴趣相同, 1757年以前, 它们的通信一直很频繁. 欧拉给达朗贝尔的信中讨论了复数和复数的对数, 他也正确地解决了复数的对数问题. 但是无论是欧拉还是其他的数学家, 复数究竟是什么,还是不清楚的,即使欧拉在1777年给出了延用至今的符号

例如,欧拉在他的《对代数的完整介绍》中说:“因为所有可以想象中的数都或者比0 大,或者比0 小,或者等于0,所以很清楚,负数的平方根不可能包括在可能的数(实数)中.从而我们必须说它们是不可能的数. 然而这种情况使我们得到这样一种数的概念,它们就其本性说来是不可能的数,因而通常叫做虚数或者幻想中的数,因为它们只存在于想象之中.”

事实上,复数的运用十分广泛,莱布尼茨在用部分分式求积分时也用到了复数,达朗贝尔、高斯对代数基本定理的证明和流体力学中也必须承认复数的存在.

1.4 复数的几何意义

正是基于以上与复数相关的发现和运用,数学家们逐渐重视研究复数试图给出复数几何解释. 虽然没有被重视,但早在1685年沃里斯已经给出过复数的几何解释,他是通过解释二次方程根的几何意义来进行的. 我们设二次方程为

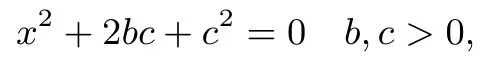
其根为

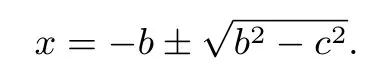
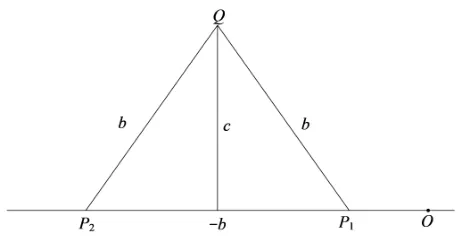
图2

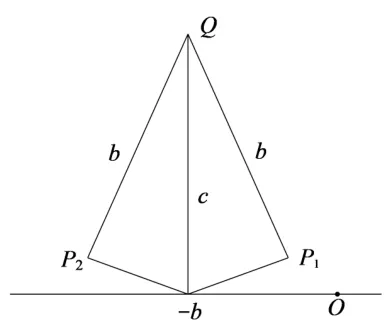
图3

因此当b ≥c时它是实根. 此时,根可以用实数直线上两点P1,P2表达,该直线由图2 所示的几何作图所决定. 当b ＜c时, 从Q出发的线段太短, 不能到达实数直线, 所以“P1,P2不可能在该直线上”,因而沃利斯“在线外(在同一平面)”去寻找它们,他的想法是正确的. 但他为P1,P2找到的位置并不恰当,它们跟他的第一次作图结果太接近了,如图3所示.

显然, 沃利斯认为+ 和-应该仍然对应着“右方”和“左方”,这将会导致不可接受的推论i=-i(在表达式中令b →0).

真正作出虚数合理解释的是韦塞尔,他出生于挪威的仲斯拉,在丹麦科学院作了多年的测量员. 1797年,韦塞尔向丹麦科学院递交论文《方向间的解析表示,特别应用于平面与球面多边形的测定》, 其中用+1 表示正方向的单位, +ε表示另一种单位,方向与前者垂直且有相同的原点. 并记作=ε,cosv+εsinv,除了虚数单位的符号不同之外,和现代复数平面的表示法一致. 可惜的是,韦塞尔的论文是用丹麦文写成的并没有得到学术界的注意.

瑞士的阿尔冈也为复数的几何解释做出了贡献, 复数的三角形式便是由他最初提出来的. 1806年,他出版了《几何作图中虚数的表示法》. 后来, 于1814年, 在热尔岗纳(Gergonne)的《数学年鉴》上有记载. 虽然韦塞尔是最先提出复数合理几何解释的作者,但由于韦塞尔的论文在据第一次发表的100 周年,才被重新翻译成法文发表. 韦塞尔的贡献也就没有得到及时的认可,所以复数平面才叫做阿尔冈平面而不是韦塞尔平面(Argang plane).

众所周知,复数的几何表示最终是由高斯完善的. 高斯的一生十分重视代数基本定理的证明,而代数基本定理的证明又依赖于对复数的承认,这就促使高斯去巩固复数的地位.1831年,高斯正式发表有关复数几何表示的论文. 他不仅将复数表示为复平面上的一点,而且阐述了复数的几何与乘法.从而高斯说到,“从几何表示法中,人们看到的直观意义的证明完全有了依据,而不需要更多的理由才能将这些量纳入算术领域之中”. 同时,为了区别a+bi 和i,高斯首先提出了复数(complex number)这个名词.

1.5 理论建立

由于以前的通讯不发达, 新知识的传播是十分缓慢的.整个18 世纪和19 世纪上半叶都在热烈的争论着复数的意义. 直到1837年,爱尔兰数学家哈密尔顿发表了论文《共轭函数理论以及作为纯粹时间科学的代数学》, 他指出复数a+bi 不是2+3 意义上的一个真正的和,加号的使用只是历史的偶然,而a是不能加到bi 上去的. 哈密尔顿对复数a+bi的代数表示进行了天才般的处理,a+bi 不过是有序实数偶(a,b). 哈密尔顿给这种数偶定义了加法和乘法,如:

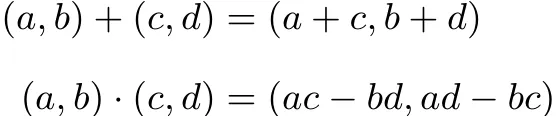
并且哈密尔顿证明了这两种运算具有封闭性, 而且满足交换律和结合律. 当然, 复数也是包括实数的, 因为只需要让b=0 就可以了. 就这样,哈密尔顿将复数用纯代数的方法定义起来了而不需要作几何解释. 事实上哈密尔顿推广了有序实数偶的思想,通过长期的摸索,他将维数推至四维,发明了四元数.

此后,复数蓬勃发展. 许多数学家跻身研究复数,如库莫尔、克罗内克、乔治·皮科克、德摩根等. 莫比乌斯发表了大量的复数几何论文, 狄利克雷将许多实数概念推广至复数,如素数.

2 复数教学的思考

2.1 复数教学的研究

《普通高中数学课程标准(2017 版)》指出:“复数是一类重要的运算对象,有广泛的应用. 本单元的学习,可以帮助学生通过方程求解,理解引入复数的必要性,了解数系的扩充,掌握复数的表示、运算及其几何意义.”国内各个版本的高中数学教材引入复数的理由也一般是为使在实数范围内无解的一元二次方程有解,如方程x2+1 = 0 无实数解,为了解决负数开平方问题,需要引入新数i 使得i2=-1. 对此,许多学者表示不满,认为使一元二次方程有复数解而引入虚数单位i 不够有说服力,随即对复数的教学展开了进一步的研究.

孔凡海、王金文、吴现、潘瑞娜等人在做复数教学设计时融入了数学史,将数学家卡当曾经研究的问题“如何把10 分成两部分使得它们的乘积为40”展现给学生来引发学生思考,使学生产生心理矛盾,进而教师提出为解决负数开方问题应引入虚数. 张小明、赵瑶瑶、闫东同样利用了数学史进行复数教学,他们化用了莱布尼茨对虚数的研究成果,即(7)式,两个复数的和为实数. 他们给学生提出了这样的问题: 已知x+y ＞0,且x2+y2= 2,xy= 2. (1)求解x+y;(2)求出x与y. 学生能计算出但无法分别求出x和y. 显然,x和y是方程x2-+2 = 0 的两个根,而这个方程是没有实数根的. 但是,x+y=√又表明x和y是存在的.由此,引发学生的思考,考虑当Δ＜0 时,方程的根应如何表示. 为了解决这一问题需要引入新数i,达到数域的扩充.

司徒超旋、李昌官、李敏瑜等人则利用卡当的一元三次方程求根公式引入复数, 当一个三次方程的三个根都是非零实数时, 求根公式就无法避免要对负数开方. 例如, 方程x3-7x+6 = 0 利用赋值法得到的三个根为x= 1,2,-3.然而利用求根公式得到的结果是:

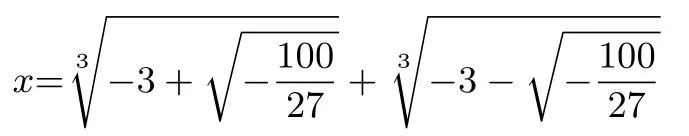
教师向学生指出赋值法与公式法求出根的一致性,数学家卡当曾经进一步计算出上式有:

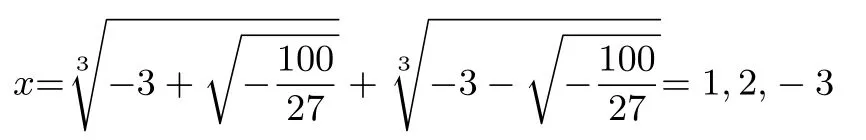
然后,教师继续引导学生讨论负数能否开方,进行虚数的引入.

卢建川认为,为使x2+1=0 这类方程有解不是引入复数的真正原因,复数的产生不仅是因为复数能解决三次方程求解问题,更因为其具有的物理背景. 因此,他对复数教学内容进行重构,利用平面向量的旋转和质点运动解释i2=-1的几何意义. 如图4 所示,1×(-1) =-1 可以看作数轴上对应1 的点绕原点O逆时针旋转180°得到-1 对应的点.而1 逆时针旋转90°得到的是纵轴上的i,所以1×i = i,即一个实数乘i 可以看作几何意义上的逆时针旋转90°,就有i2=-1,如图5 所示. 刘露对卢建川重构的复数教学内容进行了问题驱动的复数教学实验.

图4

图5

2.2 理解复数概念的理论基础

数学概念具有二重性,它的发展往往要经历由过程到对象的两个阶段. 例如,x+y既可以看作x加上y的运算过程,也可以看作运算的结果. 审视复数的发展史,数学家们如果把看作动态的过程,对-1 开方,就会认为这是不合理的,这种数只能存在于想象之中;如果经历了动态的过程而把看作一个对象进行运算,如就会产生新的理解. 于是把当作对象处理, 用i 表示可以用来四则运算、求对数、积分等,高一级的数学概念就形成了,棣莫弗公式,欧拉恒等式也就出来了. 所以,作为对象的概念,在某一个层次和更高一级层次之间起着一种枢纽作用.综上所述,复数概念的理解需要将复数对象化,将视作一个整体看待.

2.3 复数概念的认知途径

人类获得概念的方式有三种: 概念的形成、概念的同化、概念的顺应. 概念的形成是指从大量的具体例子出发,归纳概括出一类事物的共同本质属性的过程;概念的同化是指学习者利用原有认知结构中的观念来理解接纳新概念的过程;而概念的顺应则是指当原有的认知结构不能同化新概念时,就要调整或改变原有的认知结构,以便概括新概念. 概念的形成实质上是对具体事物共同本质属性的概括,比较接近与人类自发形成概念的过程. 概念的同化则较多地依赖于原有的概念,是认知水平达到一定程度的人获得概念的主要方式.教师在选取复数概念引入的方式时,应注意到高中学生在学习复数之前已经建立了“负数不能开方”这一认知图式,他们原有的数概念的认知结构难以吸收复数的概念. 显然,概念的形成和概念的同化都不适合作为复数概念的引入方式. 因此,教师应当选取概念的顺应这一方式来引入复数,通过调整或改变学生原有的认知结构,以便同化复数的概念.

2.4 复数教学的想法

复数概念教学的难点在于让学生了解复数引入的必要性、合理性和使学生以整体的眼光、以数的眼光看待a+bi.为突破这两个教学难点,首先我们应选取概念的顺应这一方式来引入复数,具体的做法是融入数学史帮助学生建立新观念:“海伦的‘平顶金字塔不可能问题’和公式法求解一元三次方程都存在负数开方问题”. 其次,z=a+bi 中加号的使用只是偶然,a是不能加到bi 上去的,复数概念从过程到对象的转变需要通过复数的几何意义——平面向量,才能明了.

2.4.1 创设复数引入的问题情境

问题一: 如图6 所示的正棱台,上下底面分别是边长为b和a的正方形,侧棱长为c,棱台的高为h. 古希腊数学家海伦推导出h可以由一个漂亮的式子给出,即h=问:若a=28,b=4,c=15,求此时的高h?

图6

问题二: 数学家卡当在其著作《大术》中给出了一元三次方程x3+px=q的求根公式

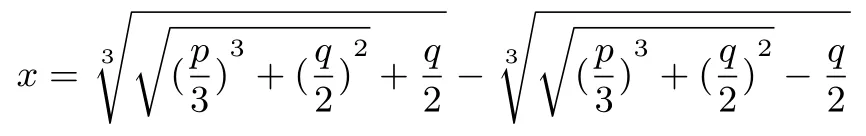
易知方程(x-1)(x-2)(x-3) = 0 的三个根为x=1,2,3;试将此方程化为x3+px=q的形式并用求根公式求解,你会得到怎么样的结果?

教师若直接向学生介绍为使x2+1=0 这样的方程有解而引入复数,他们会产生认知上的困难. 利用以上两个问题驱动学生思考,改变学生原有的观念,从而使其认识到存在负数开方问题. 又因为所以负数开方就归结为对-1 开方,引入新数也就顺理成章了.

2.4.2 复数概念的二重性与几何意义

由概念的二重性理论我们知道数学概念往往具有过程与对象两个侧面. 形成一个概念, 先经历相对直观、细节丰富的过程阶段, 上升到对象阶段时就呈现出一种静态结构的关系,成型的对象化概念利于把握整体性质,变成了易操作的实体. 我国的高中数学教科书(2019 版)一般是在引入后直接介绍到“形如a+bi(其中a,b ∈R)的数叫做复数, 通常用字母z表示, 即z=a+bi(a,b ∈R), 其中a称为复数z的实部,记作Rez,b称为复数z的虚部,记作Imz.”z=a+bi 已经是一个结构分明的“实体”,可用来做四则运算等操作性运算. 然而,z=a+bi 这一表达形式并未揭示复数概念的过程性侧面,其动态的过程不是a加上bi得到和a+bi,教师可以类比合并同类项来说明这一点,如x与xy不是同类项,x+xy是不可以合并为一个整体x(1+y).为向学生揭示复数概念的二重性,从动态过程到实体对象的转变,还需要通过复数的几何意义完成.

任何一个复数z=a+bi(a,b ∈R)都可以由一个有序实数对(a,b)唯一确定,复数的几何意义简言之就是把复数与复平面上的点一一对应, 而平面向量也是和复平面上的点一一对应的, 因此复数与复平面内的向量也是一一对应的.

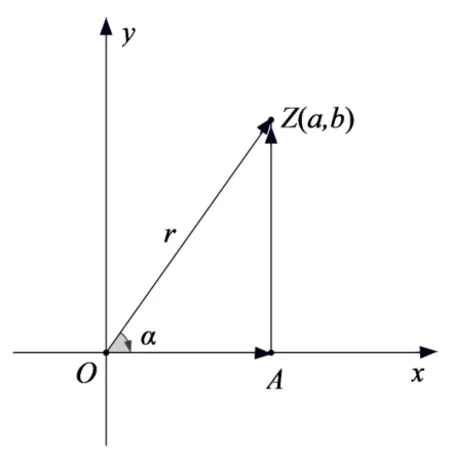
图7

建立如图7 所示的复平面. 复数z=a+bi(a,b ∈R)与向量= (a,b)相对应. 对向量进行水平和竖直方向的分解,从而有= 1rcosα+irsinα(1,i分别为x,y轴正方向上单位向量),令rcosα=a,rsinα=b则有=a1+bi,这就得到了我们的复数z=a+bi. 由此,我们通过复数的几何意义——平面向量,实现了复数概念从过程到对象的飞跃.

3 总结

通过数学史创设问题情境,教师向学生表明负数的开方涉及到数系的又一次扩充,解决负数开方的问题最后只需归结到对-1 开方,从而引入新数然后,教师向学生教授复数的几何意义时,利用平面向量的分解揭示复数概念从过程到对象的转变, 学生会对复数概念有更清楚的认识.当然,针对以上教学建议的复数教学设计是后续研究的课题.