大型稀疏线性系统的一类含参数的贪心随机Kaczmarz算法
刘 永,,崔蓉蓉
(1.常州信息职业技术学院,江苏常州213164;2.上海大学理学院,上海200444;3.盐城师范学院数学与统计学院,江苏盐城224002)
对于大规模线性系统

式中:A∈Cm×n为复数域上的m×n矩阵;b∈Cm为复数域上的m维已知向量;x∈Cn为复数域上的n维未知向量.Kaczmarz(K)算法[1]是计算其逼近解的一种非常有效的迭代算法.K算法由于其简单且收敛速度快,故被广泛应用于图像重构[2-4]、信号处理[5]和分布式计算[6]等领域.K算法的迭代公式为
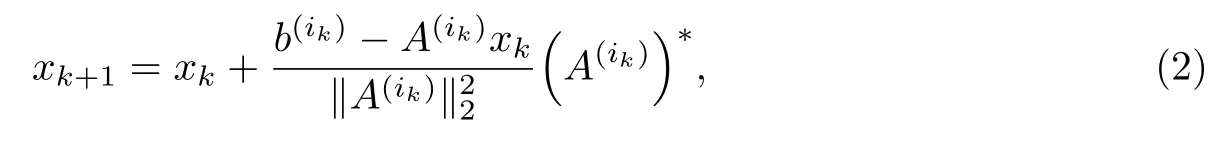
式中:(·)∗为矩阵或向量的共轭转置;‖·‖2为向量的Euclidean范数;A(ik)为矩阵A的第ik行;b(ik)为向量b的第ik个元素,ik=(k mod m)+1.从ik的选择方式可以看出,K算法的收敛速率依赖于矩阵A的行顺序,有时一个特定的行顺序可能会导致算法收敛非常慢[7-8].
为了提高K算法的收敛速率,Strohmer等[9]在2009年提出了随机Kaczmarz(randomized Kaczmarz,RK)算法,该算法依概率P(row=ik)=的大小随机选择系统(1)中系数矩阵A的某一行,并按迭代式(2)进行计算,其中表示矩阵A的Frobenius范数.Strohmer等还首次证明了当相容线性系统(1)中系数矩阵A为列满秩且m≥n,或行满秩且m≤n时,RK算法依期望指数收敛到系统(1)的唯一最小二乘解或唯一最小范数解,其收敛速率为
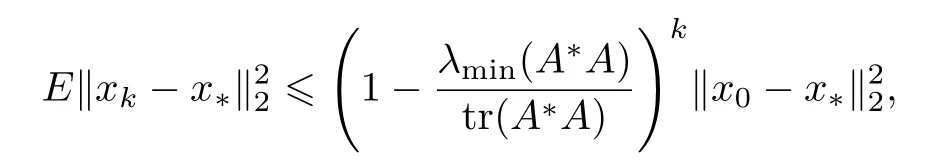
式中:x∗为系统(1)的解;λmin(A∗A)和tr(A∗A)分别为矩阵A∗A的最小非零特征值和迹.从RK算法的行选择方式可以看出,其收敛速率并不取决于方程的个数,甚至可以不需要知道整个方程组,只是通过随机选取整个方程组的一部分进行计算就可以得到系统(1)的解.因此,该算法就特别适用于规模比较大的系统,单从这点来看,RK算法优于K算法.但是RK算法中行的随机选择方式也不一定是最优的[10].例如,当为常数时,RK算法将等概率地选取A的行,此时算法的收敛速率将大打折扣.2018年,Bai等[11]提出了一种新的概率准则,即在RK算法的每个迭代步中,尽可能地选取线性系统(1)的残差向量中较大项所对应的行进行迭代计算,并在此基础上构造了贪心随机Kaczmarz(greedy randomized Kaczmarz,GRK)算法,该算法在理论和实验上都比RK算法收敛得更快.
本工作在GRK算法的迭代公式中引入松弛因子ω,构造了求解系统(1)的含参数的GRK算法.此外,本工作还给出了该算法的收敛性证明及收敛速率的一个上界.最后,通过数值实验证明了在适当选择松弛参数的情况下,本工作所提出的算法的收敛上界可小于文献[11]中算法的收敛上界.
1 贪心随机Kaczmarz算法
算法1贪心随机Kaczmarz(GRK)算法[11].
输入:A,b,ℓ和x0
输出:xℓ
1:for k=0,1,···,ℓ−1 do
2:计算
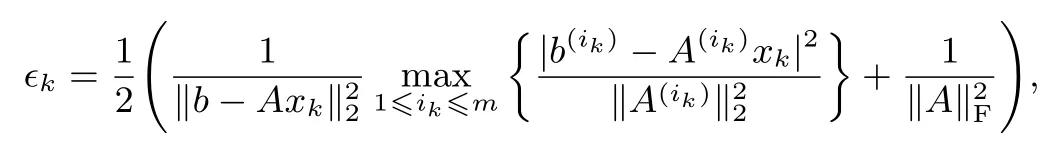
3:构造集合
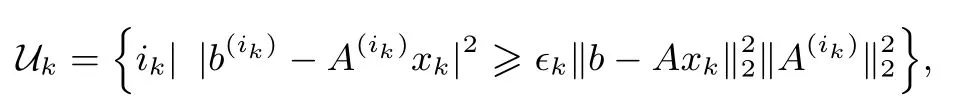
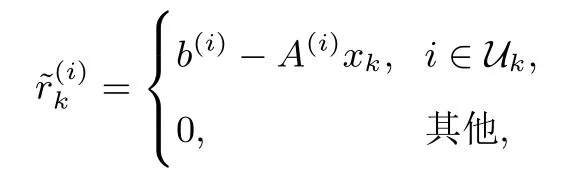
5:依概率Pr(row=ik)=选择ik∈Uk,
6:计算xk+1=.
7:end for
算法1之所以比RK算法能更高效地计算线性系统(1)的解,主要有如下2个方面的原因.
(1)在算法1的每一步迭代过程中,第3步中的集合Uk都是非空的,这是算法1能成功的保证.为了理解这一点,不妨设
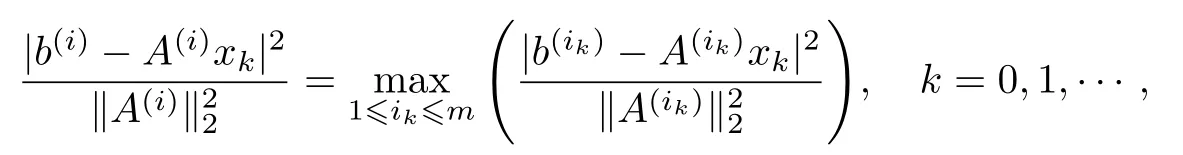
那么,可以直接得到
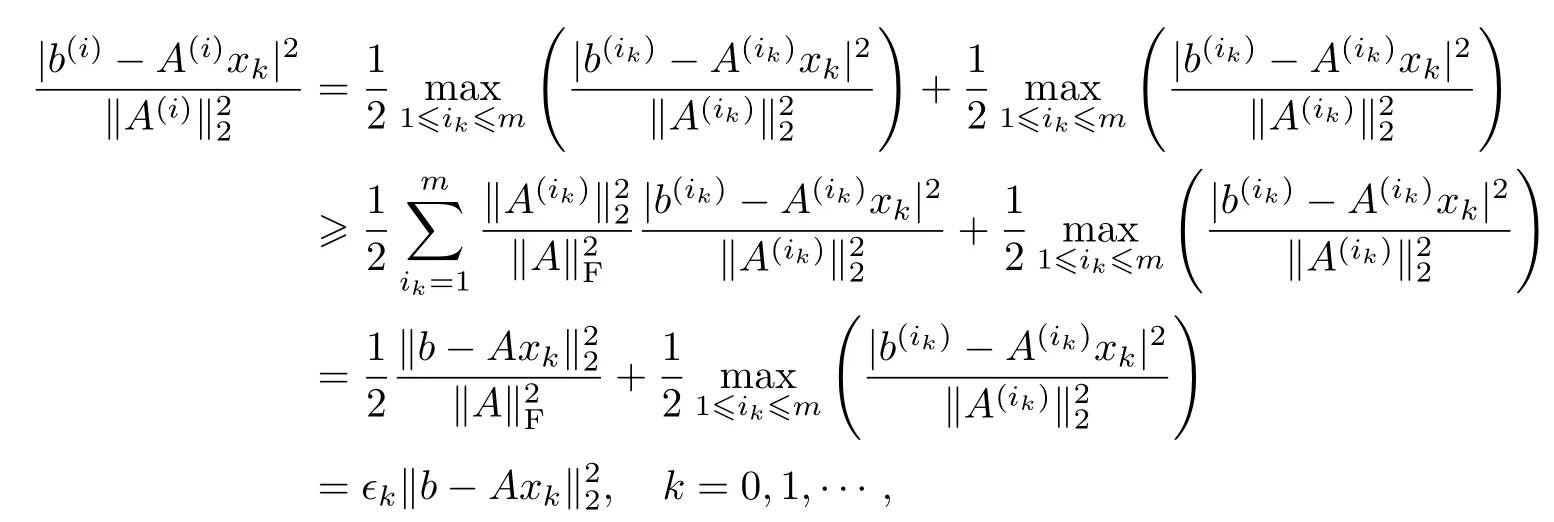
式中:ϵk如算法1的第2步所定义.于是对任意的k∈{0,1,···}都有
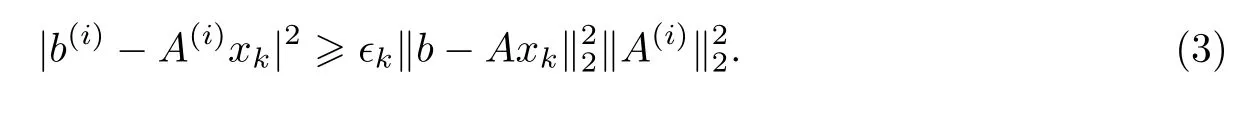
换句话说,集合Uk都是非空的.这样,算法1便能持续迭代下去.
(2)算法1比RK算法收敛速度更快,主要是因为该算法引入了一个实用的、合适的概率准则(算法1的第4~5步),能在算法的每个迭代步中尽可能地选取线性系统(1)的残差向量中较大项所对应的行进行迭代计算,这与线性方程组的求解思想是一致的,即先迭代计算方程组残差向量中最大项所在的行,这样才能以最快的速度达到方程组求解的精度要求.Bai等在理论上也证明了GRK算法的收敛速率快于RK算法,具体可参见文献[11]中的注解3.2.
2 含参数的贪心随机Kaczmarz算法
含参数的GRK算法(GRK(ω))实际上是在算法1的第6步中引入松弛因子ω,也即在GRK算法中采用如下迭代公式:
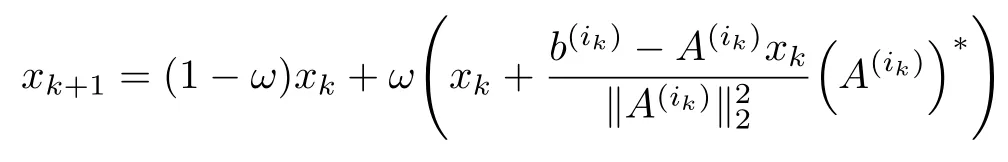
进行计算,这里ω∈(0,2)为给定的松弛因子.因此,可得如下算法2.
算法2含参数的贪心随机Kaczmarz算法(GRK(ω)).
输入:A,b,ℓ,ω和x0
输出:xℓ
1:for k=0,1,···,ℓ−1 do
2:计算
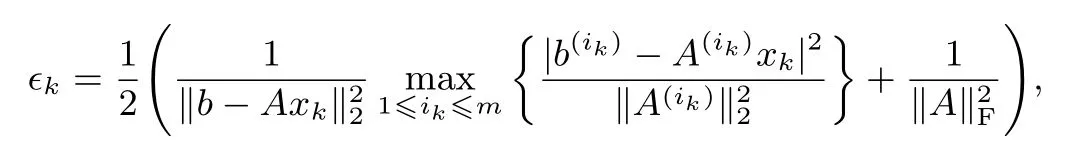
3:构造集合
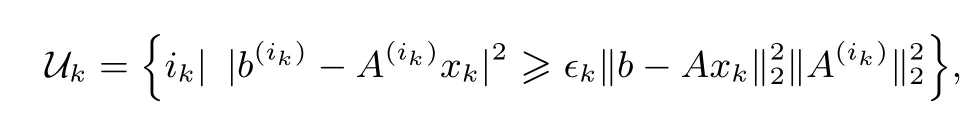
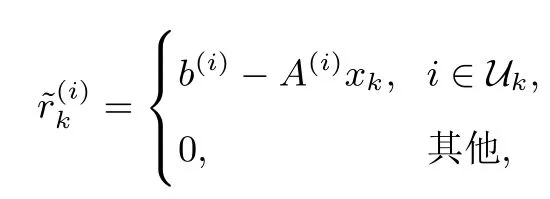
5:依概率Pr(row=ik)=选择ik∈Uk,
6:计算xk+1=(1−ω)xk+ω.
7:end for
关于算法2,有如下收敛性定理.
定理1令x∗=A†b是相容线性系统(1)的解,这里A†是矩阵A的Moore-Penrose逆,x0∈R(A∗),R(A∗)表示A∗的列空间,ω∈(0,2).那么由算法2迭代生成的序列依期望指数收敛到x∗,且解误差依期望满足
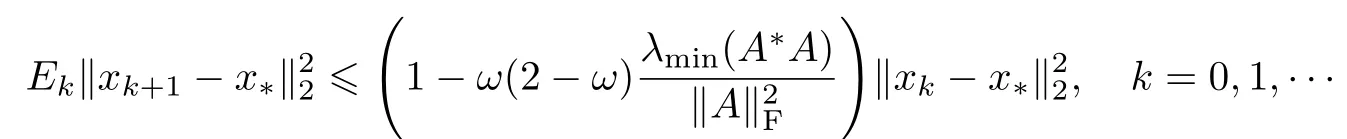
和
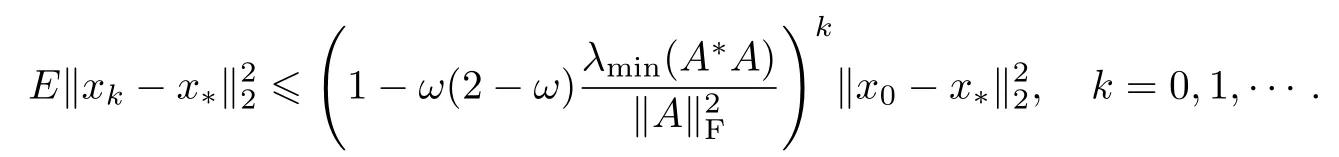
这里,用Ek表示前k次迭代的期望值,即Ek[·]=Ek[·|i0,i1,···,ik−1],这里il(l=0,1,···,k-1)表示算法在第l次迭代时选择的是第il行.同时也易知E[Ek[·]]=E[·].
证明 令Pik=,则
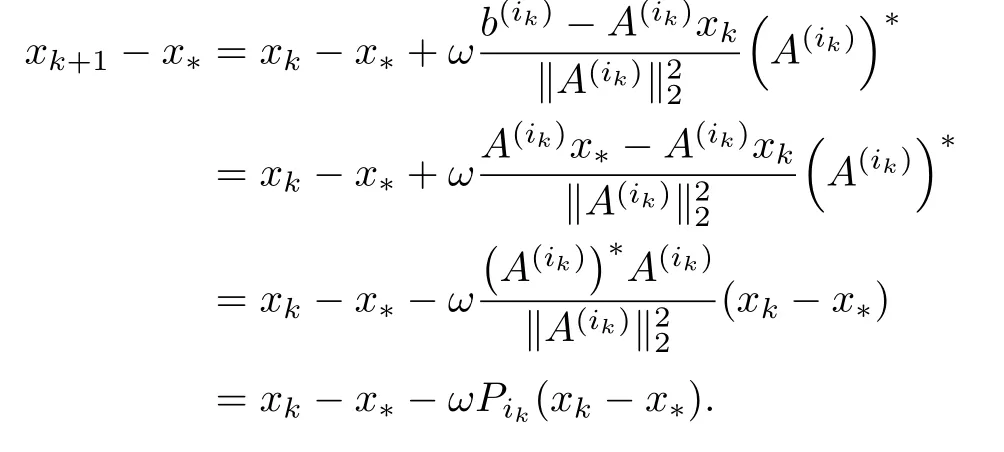
因此,
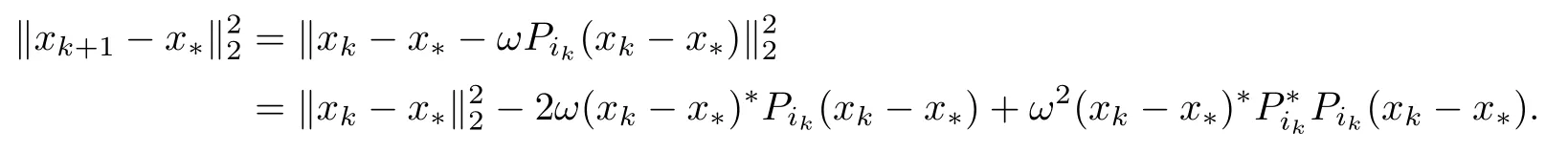
另一方面,由Pik的定义容易验证,于是可得
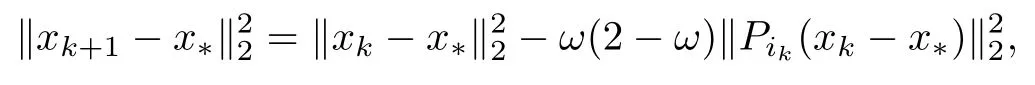
对上式两边同时取期望得
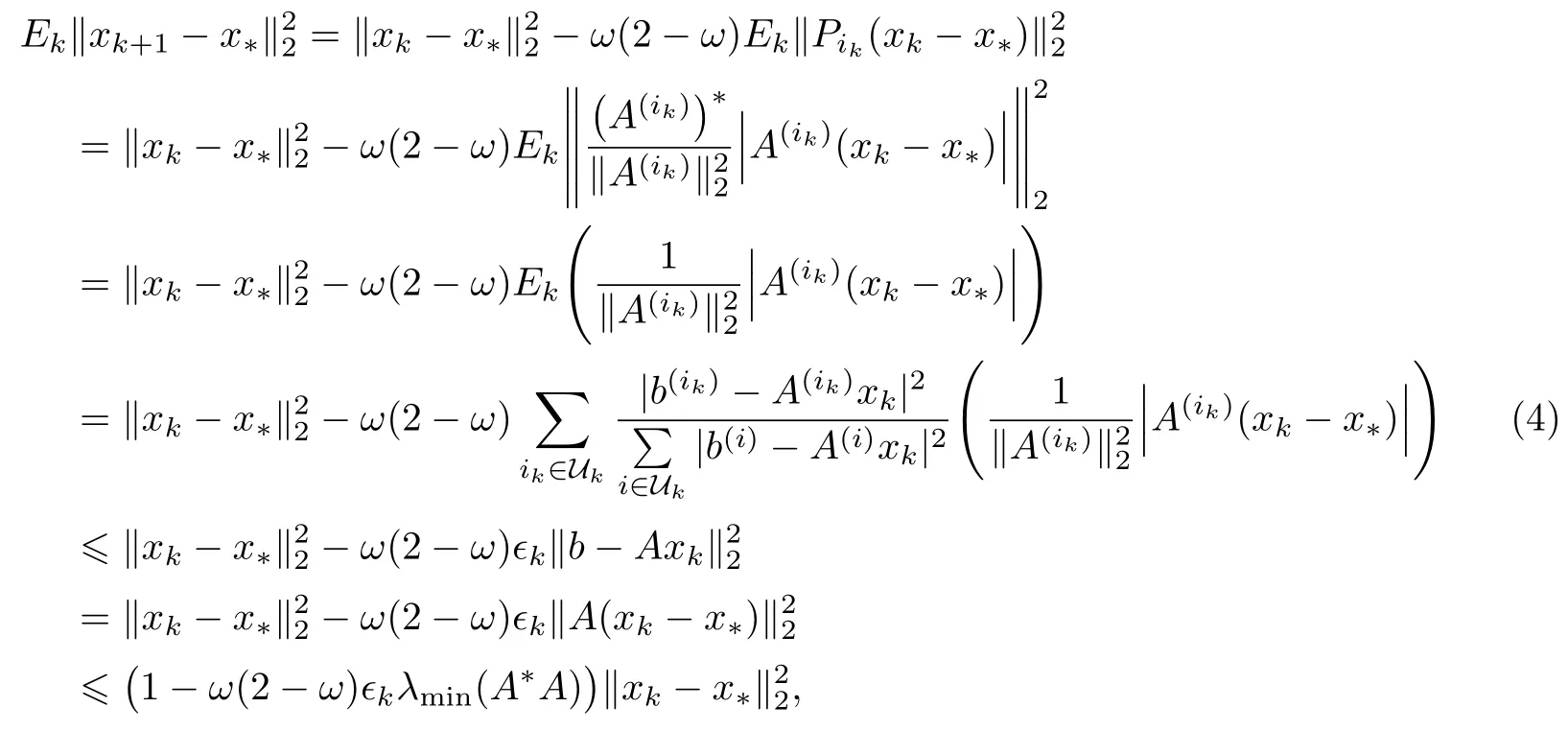
式(4)的第1个不等式可由不等式(3)直接得到,第2个不等式可由下面的估计式得到:
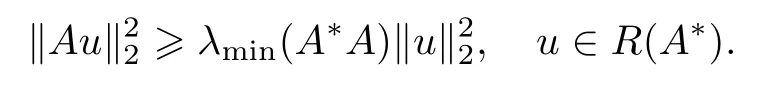
实际上,由式(4)得到的估计式还只是一个粗糙的结果,故还可以对ϵk作进一步的估计:
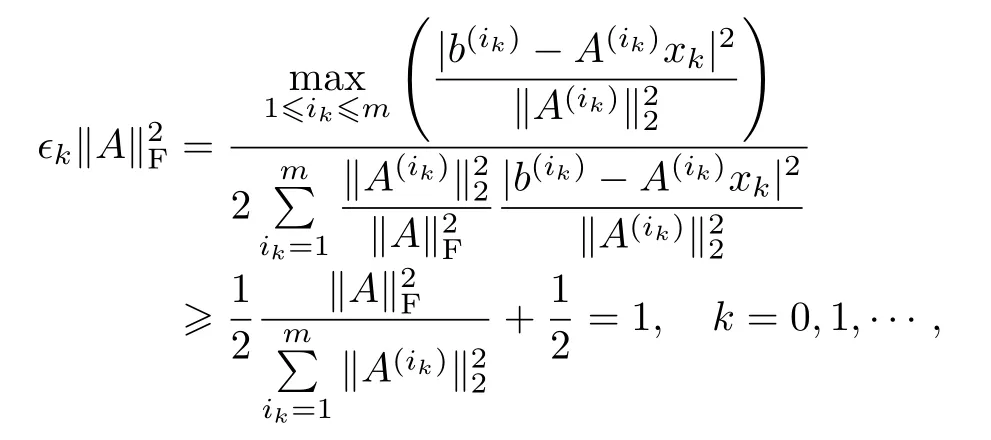
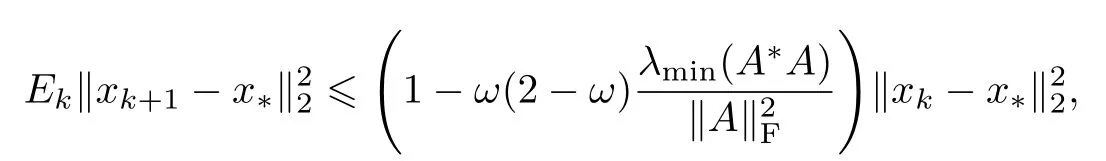
对上式两边取全期望可得
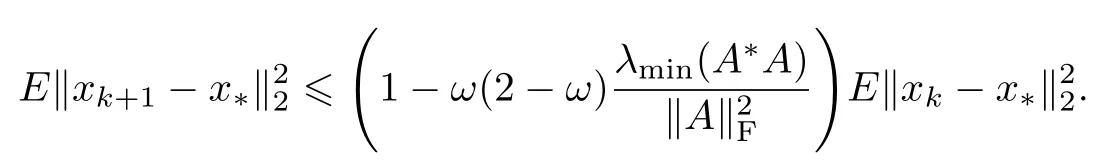
最后,可得
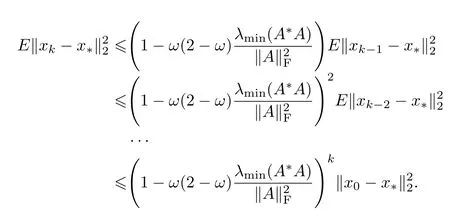
3 数值实验
用GRK算法和GRK(ω)算法求解相容线性系统Ax=b,A∈Rm×n主要有2个来源:①从文献[12]中选取6个具有应用背景的稀疏矩阵,分别是WorldCities、football及Stranke94(Pajek网络问题)和bibd−16−8、relat6以及bibd−17−8(组合问题);②用Matlab函数randn生成的随机矩阵A=randn(4 000,1 500)和A=randn(1 500,4 000).此外,设定线性系统Ax=b的解x∗=randn(n,1),右端向量b=Ax∗.本算法的数值实验是在内存为4G,主频为2.67 GHz,处理器为Intel(R)Core(TM)i5 CPU的电脑上用Matlab(R2016b)进行计算的.考虑到随机性,这里所有计算结果取10次独立实验结果的平均值.所有数值实验的初始向量均设为x0=0,停机准则设为相对解误差(relative solution error,RSE),满足
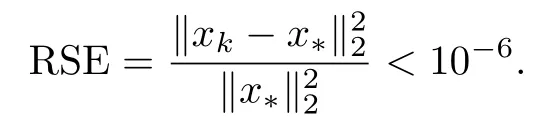
对于第一类矩阵,表1中列出了GRK算法和GRK(ω)算法在求解相容线性系统Ax=b达到精度要求时所需的迭代步(用IT表示)和计算时间(用CPU表示).同时,表1给出了测试矩阵的一些基本信息,如稠密性
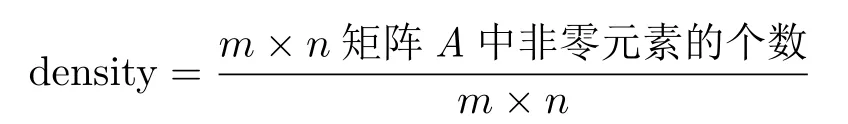
和矩阵条件数cond(A).表1中,加速比
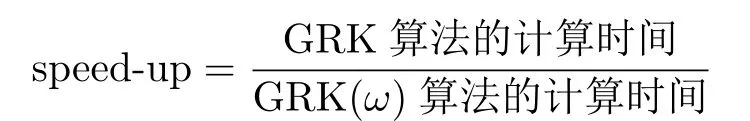
表示GRK(ω)算法相对于GRK算法在计算时间这一指标上的加速程度,其数值越大表明GRK(ω)算法对同一测试矩阵加速得越快.从表1中可以看出,对于矩阵A,无论m≥n还是m<n,当选取合适的参数ω时,GRK(ω)算法在迭代次数和计算时间方面都优于GRK算法,并且有显著的提速,加速比(speed-up)最高可取3.03(见矩阵Stranke94).
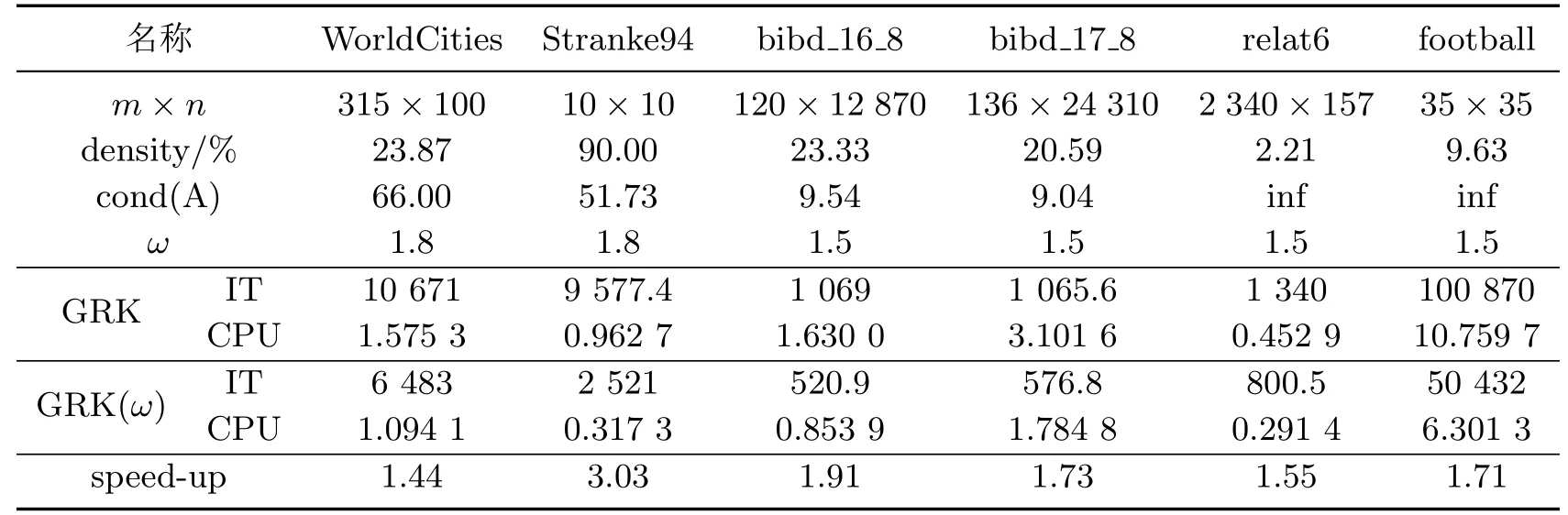
表1 在不同系数矩阵下求解线性系统(1)的GRK算法和GRK(ω)算法的数值结果Table 1 Numerical results of GRK and GRK(ω)algorithms for solving linear system(1)under different coefficient matrices A
对于第二类矩阵,分别描绘了GRK算法和GRK(ω)算法对于2种不同的系数矩阵A,log10(RSE)随迭代步和计算时间的变化曲线图(见图1和2).从图中可以看出,本算法是可行的,并且在选择适当的参数后比GRK算法收敛得更快.
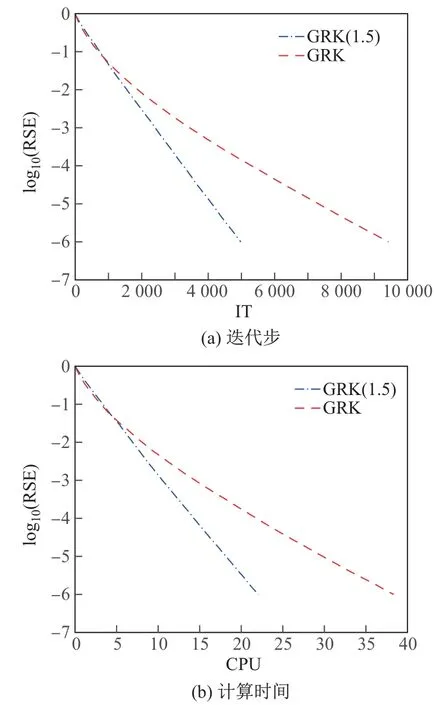
图1 当线性系统(1)的系数矩阵A=randn(4 000,1 500)时,GRK算法和GRK(1.5)算法的log10(RSE)的变化曲线Fig.1 Curves of log10(RSE)for GRK and GRK(1.5)algorithms when the coefficient matrix of linear system(1)is A=randn(4 000,1 500)
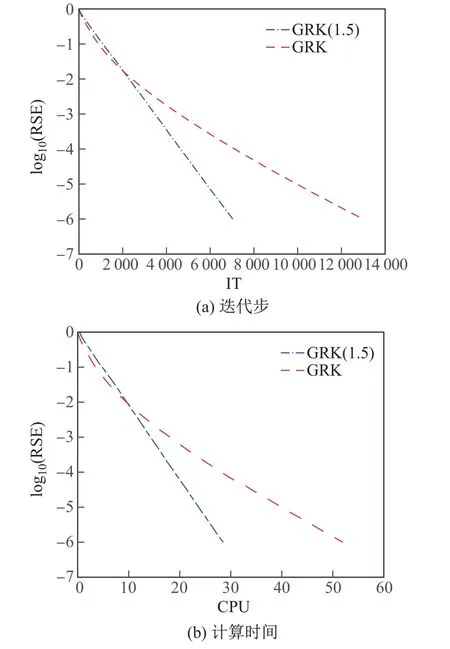
图2 当线性系统(1)的系数矩阵A=randn(1 500,4 000)时,GRK算法和GRK(1.5)算法的log10(RSE)的变化曲线Fig.2 Curves of log10(RSE)for GRK and GRK(1.5)algorithms when the coefficient matrix of linear system(1)is A=randn(1 500,4 000)
4 结束语
本工作在贪心随机Kaczmarz(GRK)算法的基础上,提出了一类含参数的GRK(GRK(ω))算法,分析了算法的收敛性.数值结果表明,在选择适当参数ω后,GRK(ω)算法在迭代步和计算时间方面明显优于GRK算法.在数值实验中,对于不同的系数矩阵参数ω是通过多次实验使得迭代解在达到停机准则时所需迭代步相对最少来确定的,自适应的参数选择策略(ωk随迭代步的变化而变化)可能会获得更好的数值结果.

