偏心桨机构水下旋转桨式步态水动力建模
李小毛,彭 宇,李天波,陈俊杰,徐 佳,崔建祥
(上海大学机电工程与自动化学院,上海200444)
近年来,随着机器人技术和相关理论的不断发展,两栖机器人逐渐成为国内外科研机构关注的热点.两栖机器人对于多种环境和地形介质具有良好的适应性,能够协助或替代作业人员在恶劣多变的两栖环境中执行各种危险、复杂的任务,在抢险救援、灾后勘察和科学考察等领域具有广泛的应用前景.
根据推进方式和系统方案的不同,可将现有的两栖机器人分为2类:运动仿生型和融合推进型.运动仿生型两栖机器人的机构和系统设计模仿了生物的运动特征和原理.Yang等[1]设计的FroBot机器蛙,通过一对仿蛙脚蹼的摆动鳍重现了青蛙的游泳方式;Yamada等[2]研制的蛇形两栖机器人ACM-R5采用轮桨式推进机构作为关节模块,可在水中和陆地上蜿蜒前进;Low等[3]研发的海龟机器人,通过模仿海龟鳍状肢的形状和运动方式设计类似的推进结构,实现了水陆两栖作业;Jun等[4]研制了利用六足机构在海滩或海底步行的机器蟹CR200;此外,Crespi团队[5]开发的Salamandra RoboticaⅡ机器人在仿生方面更进了一步,利用人工神经元模拟蝾螈脊髓神经中枢的功能,可根据地形变化自主选择合适的爬行和游泳模式.融合推进型两栖机器人则是通过整合或切换多种推进机构来实现高两栖机动性能.Georgiades等[6]开发的Aqua机器人,通过更换刚性腿和柔性桨来实现两栖运动;由Li等[7]设计的两栖球形机器人,在水下采用喷射推进,陆上通过轮-腿复合机构移动;中科院Yu等[8]开发的机器人Amphibot-Ⅱ,独创轮-桨-鳍融合式推进机构,依靠3种推进机构分工合作实现水陆两栖能力;此外,Liu等[9]设计的自适应轮-腿式机器人,由大直径轮腿复合机构驱动,能在不同环境下切换运动模式以提高运动效率.然而,由于机器人运动和适应能力的局限性,现有的两栖机器人很难应用于海啸、泥石流等灾害发生后的复杂环境中.为了提高机器人在复杂两栖环境下的通过能力,本工作设计了一种基于行星轮系和偏心桨(eccentric paddle,ePaddle)的复合型两栖运动推进机构ePaddle[10].在前期研究中,通过设定不同机构的桨叶轴位置以及外轮旋转模式,实现了轮式、腿式和轮腿融合式等陆上步态[11],以及旋转桨式、摆动桨式水下步态[12-13],其中旋转桨式步态下的机器人具有更高的巡航速度,适合在开阔水域航行.
构建合理准确的水动力学模型,对分析水下机器人的运动特性和制定控制策略具有重要意义.针对桨叶形状、材料和运动方式的不同,研究人员提出了多种水动力学模型,其中刚性桨模型[14]和Lighthill模型[15]的应用较为广泛.前者适用于同一水深下的桨叶推力预测,简化了流体在不同深度产生的影响;后者虽适用于细长桨叶的摆动推力分析,但忽略了流体作用于桨叶的表面力.此外,Park等[16]提出了适用于柔性桨的伪刚体(pseudo-rigid-body,PRB)模型,将柔性桨简化为通过铰链和扭簧连接的刚体进行分析;王海龙[17]提出可通过求解Navier-Stokes方程分析机构水动力性能,但该方法在复杂流体环境中不能求得精确的数值解.
本工作通过构建ePaddle机构在水下以旋转桨式步态运动过程中的水动力模型来分析其水下推力特性.首先,简单介绍了ePaddle机构和旋转桨式步态,并构建应用于水下旋转桨式步态的推力预测模型;其次,在此基础上进行了实验验证与讨论;最后,进行总结并提出未来的研究规划.
1 ePaddle机构与水下旋转桨式步态
ePaddle概念由Sun等[18]首次提出(见图1).ePaddle机构有3个自由度:独立驱动的外轮壳体、两自由度平面运动的桨叶轴和围绕桨叶轴被动旋转的桨叶.轮壳旋转过程是通过调整桨轴的偏心距rS和偏心角θS,调节桨叶的姿态以及伸出轮壳外的长度来进行的.表1列出了其机构参数.
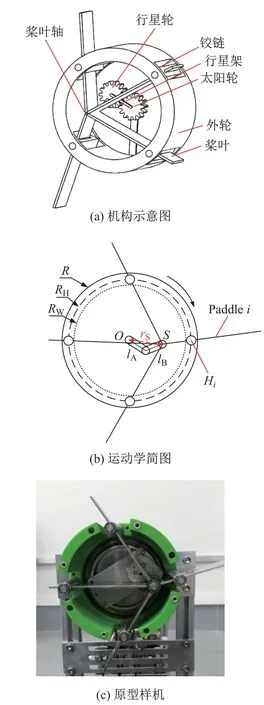
图1 ePaddle机构Fig.1 Mechanism of ePaddle

表1 ePaddle模块规格Table 1 Specifications of ePaddle module
ePaddle水下旋转桨式步态如图2所示,以外轮旋转一周为一个步态周期.在初始状态下,桨叶轴S被置于相对于外轮中心轴O的偏心位置.当外轮绕中心O沿固定方向旋转时,轮壳带动4个桨叶绕桨叶轴S旋转产生推力,进而推动机构在水中向前运动.通过调节桨叶轴相对于轮心的位置,可以改变外轮旋转过程中4个桨叶伸出外轮接触水体的长度和面积,进而控制机构产生推力的大小和方向.
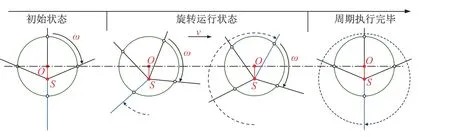
图2 旋转桨式步态相序Fig.2 Rotational paddling gait sequence
类似地面上轮胎的打滑现象,ePaddle机构水下运动时也会发生“打滑”现象,参考轮式移动机器人使用的滑差率定义,机构水下打滑程度可由滑差率s表示:

式中:v为机构水下水平运动速度;R为外轮半径;ω为外轮转速.
2 旋转桨式步态动力学模型
本工作基于文献[19-20]中提出的方法,使用Morison方程构建ePaddle机构的推力预测模型,其坐标系如图3所示.ePaddle机构在执行旋转桨式步态时会产生水波,其波长远大于机构桨叶截面等效直径,故适用Morison方程.本工作作如下简化假设:

图3 ePaddle机构坐标系Fig.3 Coordinate system for ePaddle mechanism
(1)假设流体为无旋且不可压缩的黏性流体;
(2)根据运动的相对性,机构在水下以一定速度水平匀速运动,转化为水流以大小相同、方向相反的速度流过固定位置上的机构,机构执行旋转桨式步态产生的微小流速变化相对于水流速度可忽略不计;
(3)机构运行时轮内桨叶与流体的作用可忽略不计.机构运动时受到的流体力FS为外轮-流体之间的作用力FW,与桨叶伸出外轮部分产生的有效推力F的矢量叠加,即

为探究机构旋转桨式步态的动力学特性,本工作主要研究机构执行旋转桨式步态时产生的有效推力F(文中所指推力全部为有效推力F).
图4为桨叶受力分析及坐标系定义.图4(a)中,以外轮轮心O为原点建立惯性坐标系{xglobal,yglobal,zglobal},桨叶宽度为B;桨叶长度为L;厚度为A;=[Vx,Vz]T是惯性坐标系下的水流速度.由假设(2)及式(1)可知

当外轮转速不变时,水平流速大小仅与滑差率s有关,且s越大水平流速越小.
以桨轴中心S为原点,在桨叶i上建立桨叶坐标系,其中x轴沿桨叶方向向外,z轴方向垂直于桨叶.从惯性坐标系转换到桨叶坐标系的旋转变换矩阵为
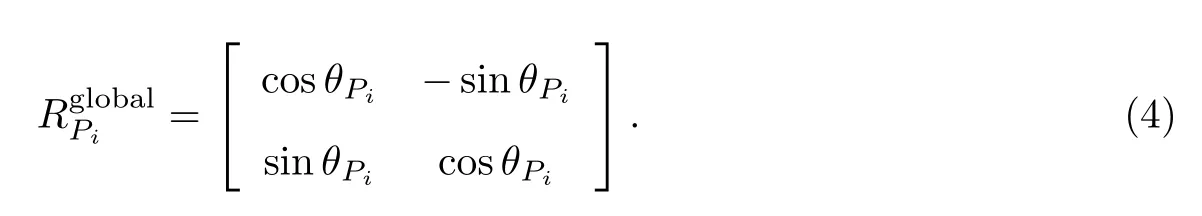
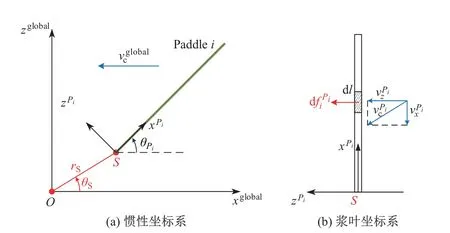
图4 桨叶受力分析及坐标系定义Fig.4 Schematic of thrust analysis on a paddle and coordinate system
图4(b)中,在桨叶坐标系中采用微元法对一小段桨叶dl进行水动力求取,求得水平流速在桨叶坐标系下的速度:

参考文献[19],利用Morison方程变形式求出在桨叶坐标系下微元dl所受水动力:
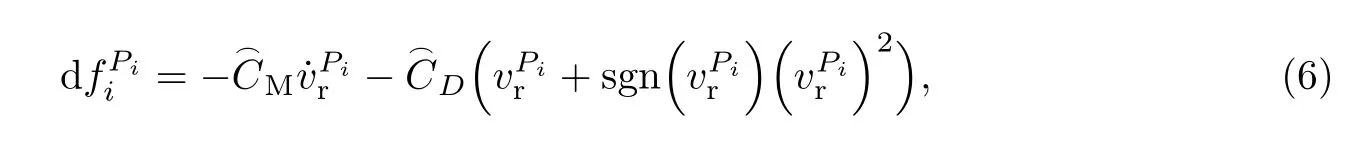

式中:ρ为水的密度;和分别为桨叶坐标系下x和z方向的绕流拖曳力系数;是z方向上的附加质量系数.由于桨叶为细长体,故x方向上的附加质量系数可忽略不计.实验环境中雷诺数Re为105级别,据此系数经验值[21]取.
由式(6)得到受力微元dl所受水动力,通过沿伸出外轮的桨叶长度进行积分可求得在桨叶坐标系下伸出外轮桨叶部分产生的推力:

由运动学分析可得第i个桨叶伸出外轮的桨叶长度
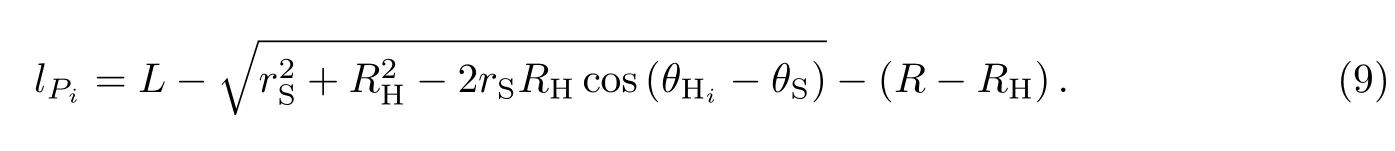
将桨叶坐标系下的推力旋转变换到惯性坐标系下,即可求得单个桨叶i在某一时刻的推力

进而求得一个ePaddle机构4个桨叶产生的推力:
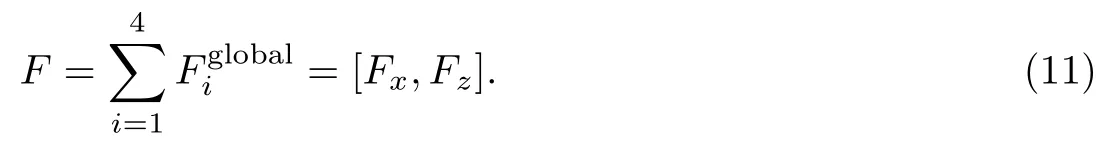
3 水下推力测试实验
3.1 实验设置
本工作设计了3组实验,分别验证在旋转桨式步态下,不同桨轴偏心角θS、桨轴偏心距rS和外轮转速下滑差率s对ePaddle机构水下推力特性的影响,实验参数如表2~4所示.为保证实验的准确性和可重复性,每组实验重复10次取平均值作为实验结果,同时使用离散小波变换(6层db6小波)滤除实验台机架振动、白噪声等引起的噪声干扰,提取原始推力信号.为分析在不同滑差率下由桨叶产生的推力,最终实验结果设为传感器测得机构产生的推力减去相同实验参数下零桨配置机构产生的阻力得到的净推力.

表2 2种桨轴偏心角下滑差率影响推力特性的实验参数Table 2 Experimental parameters for identifying effects of slip ratio in two different eccentric angles

表3 不同桨轴偏心距下滑差率影响推力特性的实验参数Table 3 Experimental parameters for identifying effects of slip ratio in different eccentric distances

表4 不同外轮转速下滑差率影响推力特性的实验参数Table 4 Experimental parameters for identifying effects of slip ratio in different rotational speeds
3.2 力学测试平台
本工作在2.3 m×1.8 m×1.7 m尺寸的水箱内搭建了力学测试平台(见图5),测量ePaddle机构在执行水下旋转步态时所受的水动力.ePaddle机构安装在支撑平台上,可通过导轨和直流伺服电机驱动滚珠丝杠(BSSR2505-1420,MiSUMi)带动ePaddle机构实现水平移动.ePaddle机构和支撑平台间固连有一个6轴力传感器(F/T Delta SI-330-30),用于测量ePaddle机构在实验时所受到的水动力.在实验过程中,整个ePaddle机构完全浸没在水中,由3个直流电机(RE30,Maxon motor)通过同步带轮驱动.3个电机装有减速器和增量式编码器,由Copley ACJ-055-09驱动器分别驱动,通过CANopen通讯协议由NI PXI-1042Q控制箱控制.控制箱接入的数据采集卡以1 000 Hz的采样频率对力传感器以及编码器反馈的数据进行实时采集,所有控制和数据采集程序在Labview软件环境运行.

图5 力学测试平台Fig.5 Mechanical test platform
3.3 实验结果
不同实验参数下测得的结果与由Matlab仿真得到的预测结果对比情况如图6~10所示(图中实线为实验值,虚线为理论值).从图中可以看出,机构产生的瞬时推力实验值均呈类正弦曲线形态,一个旋转周期内有4个波峰和波谷,3组实验结果的对比验证了推力预测模型的准确性.当外轮转速增大时,z方向上的实验结果与预测结果偏离较大,估计是由于高外轮转速产生了更大的水波,从水箱壁上反弹的回波作用于桨叶造成了水动力的耦合.
(1)不同桨轴偏心角下滑差率对机构推力的影响.图6为2种桨轴偏心角配置下不同滑差率产生的推力对比结果.图中,随着滑差率变大,机构产生的水平推力显著减小,而竖直推力值差别较小.当滑差率小于0.9时,2种桨轴偏心角下的机构均可在水平方向上产生正向推力,推动机构前进.此外,在桨轴偏心角为-90◦时,水平推力整体大于偏心角为0◦时产生的水平推力,但此时在竖直方向上产生了更大的下沉力.
(2)不同桨轴偏心距下滑差率对机构推力的影响.图7为桨轴偏心距为30 mm时机构在不同滑差率下产生的推力对比结果.随着滑差率增大,机构的水平推力显著减小.通过图8中不同桨轴偏心距下峰值推力的对比可以发现,随着桨轴偏心距的增大,桨叶会产生更大的峰值推力,且随着滑差率增大,水平峰值推力呈线性减小的趋势,而竖直峰值推力的变化较小.与图6进行对比可知,桨轴偏心距增大,机构在相同转速下能在一个周期内更快达到峰值推力,此时瞬时推力曲线的幅值会显著增大,特别是在竖直方向上.
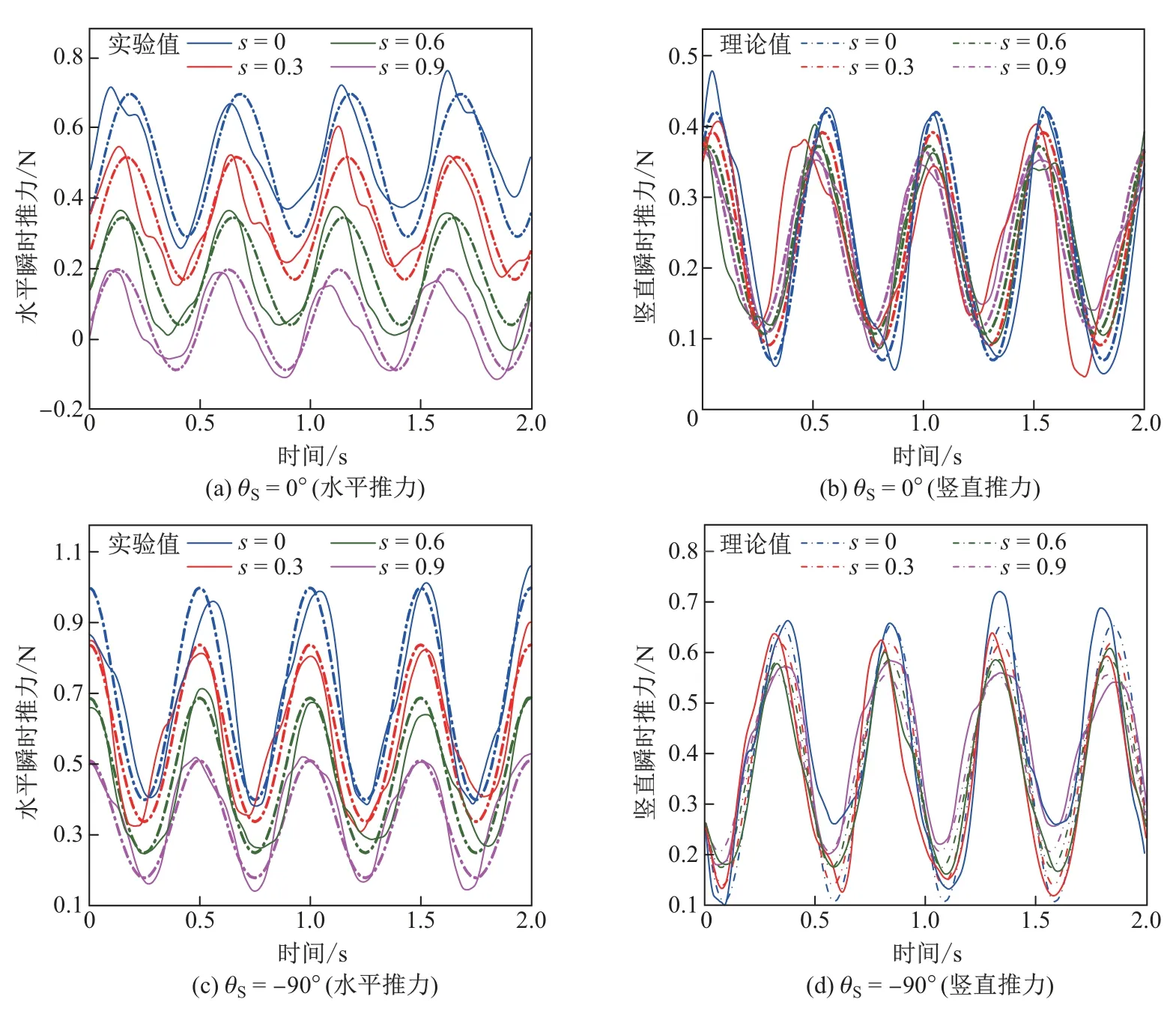
图6 2种桨轴偏心角配置下不同滑差率产生的推力对比Fig.6 Thrusts in x-and z-axis direactions with differentθS in different slip ratios
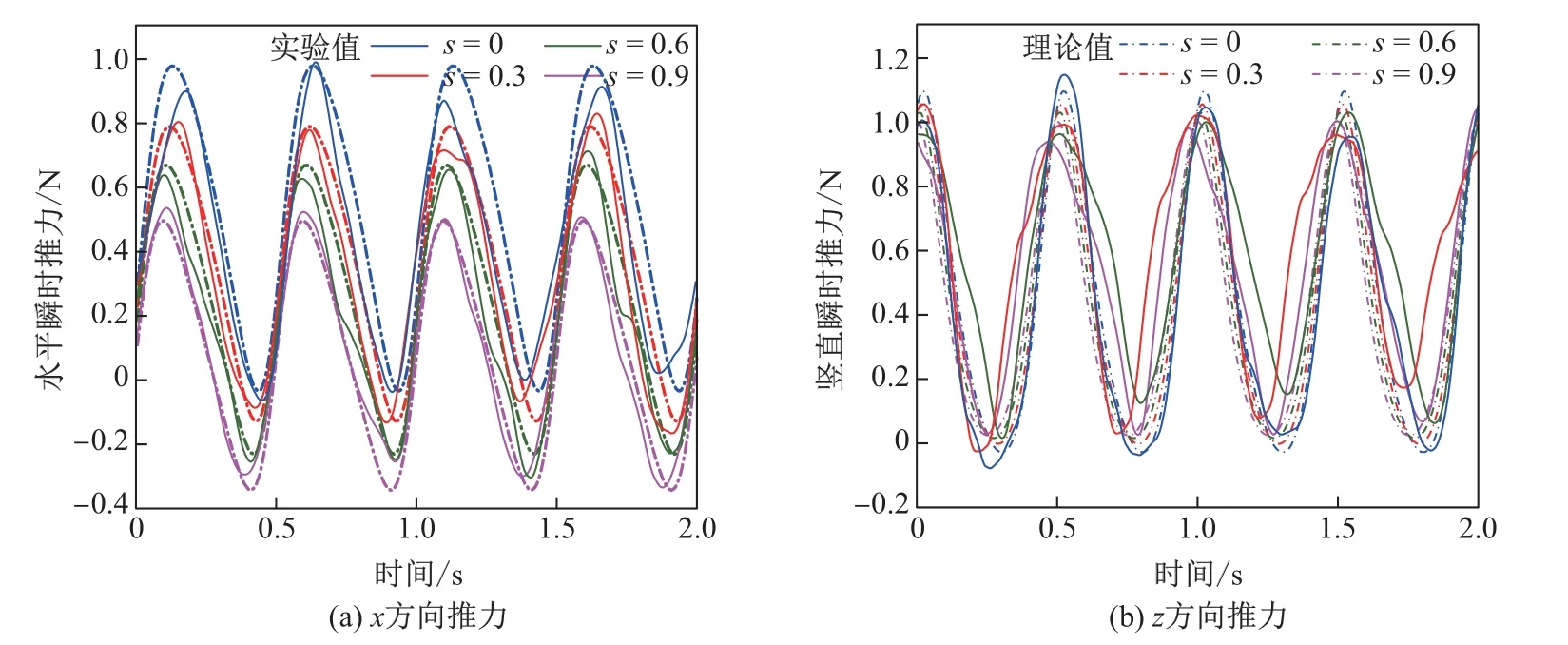
图7 桨轴偏心距为30 mm时滑差率变化产生的推力对比Fig.7 Thrusts with 30 mm eccentric distance in different slip ratios
(3)不同外轮转速下滑差率对机构推力的影响.图9为机构在外轮转速为60 r/min时不同滑差率下产生的瞬时推力的对比结果.随着滑差率的增大,机构在水平方向上产生的推力值显著减小.与外轮转速为30 r/min时测得的实验结果相比,瞬时推力值提高了2倍以上.图10为机构在不同外轮转速下滑差率变化产生的平均推力图.从图10可以看出,随着外轮转速的提高,桨叶产生的平均推力值显著增大,且随着滑差率的增大,水平方向上的平均推力值线性减小,而竖直方向上的平均推力基本保持不变.

图8 不同桨轴偏心距下滑差率变化产生峰值推力对比Fig.8 Peak thrusts with different eccentric distances in different slip ratios
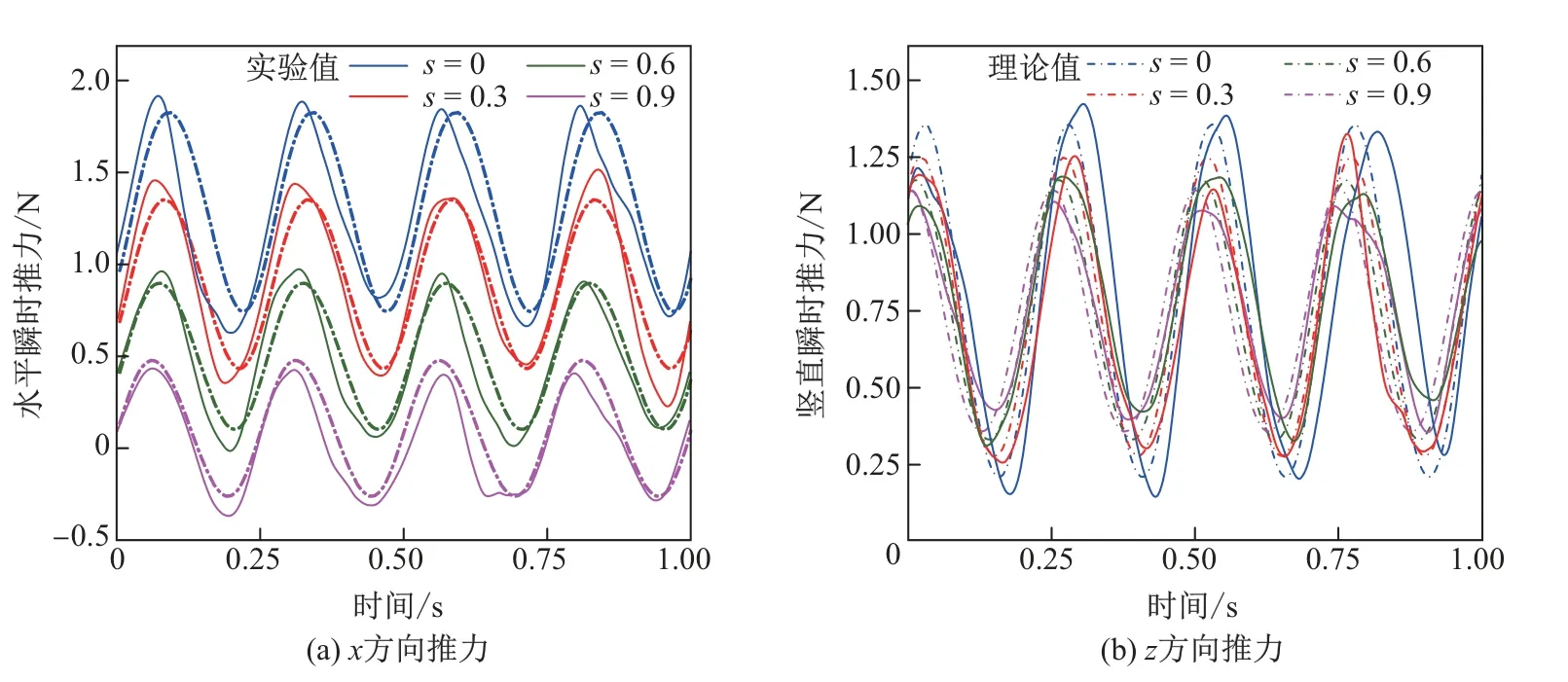
图9 外轮转速为60 r/min时滑差率变化产生的推力对比Fig.9 Thrusts with 60 r/min rotational speed in different slip ratios
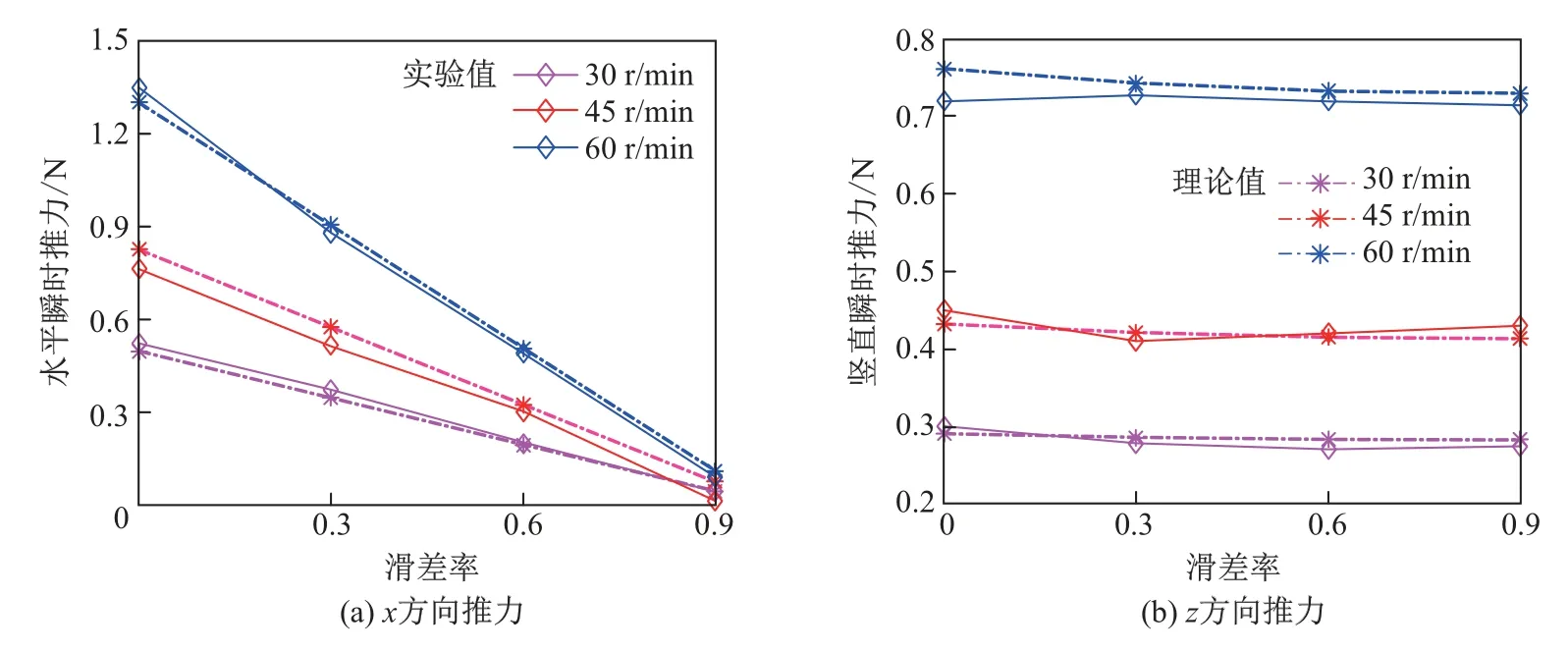
图10 不同外轮转速下滑差率变化产生的平均推力对比Fig.10 Average thrusts with different rotational speeds in different slip ratios
3.4 讨论
通过上述实验结果可知,不同运动配置参数下的机构在执行旋转桨式步态时,产生的水平推力随着滑差率s的增大而减小,而竖直推力受滑擦率影响较小.由式(3)可知,当滑差率s增大时,水流的水平流速Vx减小,桨叶相对于水流的速度也相应减小,而桨叶所受到的水动力与桨叶相对于水流的速度成正比(见式(6)).因此,可通过减小ePaddle机构运动的滑差率来提高推进效果,同时保持机构理想的运行状态.
不同桨轴偏心角配置下的推力实验结果表明,在合适的滑差率下(s<0.9),2种配置下的机构执行旋转桨式步态时均可在前进方向上做正功,即在保证较高的运动速度的同时,产生较为理想的推进力.偏心角为-90◦配置下的机构能产生更大的正向推力,可高效推进机构前进,实现更快的加速度和巡航速度.针对机构在运行过程中产生竖直下沉力的问题,可以通过加装浮力材料来抵消其影响.
对于不同桨轴偏心距配置下推力的实验结果表明,增大偏心距会产生更大的峰值推力.通过式(8)、(9)可知,当桨轴偏心距rS增大时,一个周期内伸出外轮的最大桨叶长度lPi,max会增大,增大了水流作用于桨叶上的面积,从而可以产生更大的峰值推力,同时桨叶伸出长度的变化幅度也会增大,使推力幅值变大.大桨轴偏心距下机构可以更快地达到峰值推力,但在竖直方向上会引起明显的推力波动,说明较大的桨轴偏心距会破坏机构在竖直方向上的运动稳定性.
4 结束语
本工作构建了ePaddle机构执行旋转桨式步态时的推力预测模型,分析了不同配置参数对机构推力特性的影响,并通过实验验证了该模型的准确性,为制定机器人运动控制策略提供了理论基础.结果表明,机构水平推力随滑差率的增大而减小;-90◦桨轴偏心角的配置可提供更大的前进推力,更适合实际应用;增大桨轴偏心距可增大机构的峰值推力,而提高外轮转速可明显增大平均推力和提高推进效率.在未来工作中,将基于本工作的结论,研究采用多个机构的两栖机器人执行旋转桨步态时的步态规划与协调控制问题.

