无人水面艇操纵模型分级辨识方法

袁晓宇,黄承义,彭 艳,瞿 栋,刘东柯

(1.上海大学无人艇工程研究院,上海200444;2.国家海洋局北海海洋工程勘察研究院,山东青岛266061;3.上海大学计算机工程与科学学院,上海200444)

作为一种水面无人移动平台,近年来无人水面艇在海洋资源勘测[1]、环境监视和侦察[2]、灾后搜索与救援[3]、近岸港口安防[4-5]以及同其他有人、无人系统协同作业[3,6]等方面得到了广泛的应用.因此,开展无人水面艇(unmanned surface vehicle,USV)的相关技术研究,进一步提高无人水面艇的智能化程度,对提升我国海洋装备水平具有重要意义.然而,由于①环境干扰信息(风、浪、涌)的不确定性,导致了控制器面临不可预测的环境扰动;②无人水面艇具有非线性和时变性的动力学特性,并且艇体的转艏模型与其航速高度耦合,这些都对无人水面艇模型参数的辨识以及基于模型的控制算法的设计提出了更大的挑战.

围绕无人水面艇的建模问题,Fossen[7]提出了6自由度无人水面艇动力学模型,并通过操纵实验计算了动力学因子,得到了精确的动力学模型,并通过实验验证了该模型的有效性.但是该动力学模型相对复杂,不利于实际工程应用.陈霄等[8]提出了一种基于分步实艇数据处理的模型参数辨识算法,详细设计了辨识算法的步骤和流程,并通过湖上操纵性试验获得模型参数.该方法考虑了无人水面艇操纵模型参数辨识过程中存在的“参数相消效应”,但没有进一步研究风、浪、流等外界不确定干扰下的无人水面艇模型参数估计及校正问题.利用Z形和回转实验获得的数据,江立军等[9]通过递推最小二乘法辨识出无人水面艇的数学模型,并通过仿真与实船实验的结果对比,验证了该模型的准确性和合理性.崔健等[10]通过不同航速和不同舵角下的一系列船模Z形操纵试验得到了复合三体船模的操纵模型.以上学者都采用操纵实验来获得无人水面艇模型参数的方法,也有一些学者采用简化版的Nomoto模型进行试验.Nomoto操舵模型由Nomoto等[11]提出,该模型将舵角和转艏角速度关联起来,得到了一种简单直接的动力学模型;Norrbin[12]将非线性因子加入到Nomoto模型中,得到了非线性的Nomoto模型,提高了无人水面艇转艏模型的精度;Velasco等[13]推导出包含运动学和动力学的1阶Nomoto转艏模型,通过圆形机动实验对模型参数进行辨识,并设计了艏向控制器来进行实验验证;Sonnenburg等[14]提出了速度分段辨识的方法,针对无人水面艇在低速时侧滑较大的问题设计了1阶滞后模型(Lag model),而在高速阶段由于可以忽略侧滑的影响,故采用1阶Nomoto模型.为了获得更精确的操纵模型,一些学者则采用优化算法来获取非线性模型.Sharma等[15]采用遗传算法得到了基于多层感知机(multi-layer perceptron,MLP)、递归神经网络(recurrent neural network,RNN)[16]和径向基网络(radial basis function,RBF)的非线性模型,并通过均方误差分析和残差关联分析,得出了基于递归神经网络的模型辨识效果优于其他模型的结论,但是该模型在实际工程应用中对算力要求较高.因此,在实际操作中如何兼顾精度和计算资源限制,选择最优的模型辨识方法依然是无人水面艇研究与应用中亟待解决的难题.

本工作采用分级辨识思想,分别对舵角和艇体转艏进行了模型辨识,并针对艇体转艏模型和航速高度耦合的问题,提出了在低速、中速和高速段分别进行模型参数辨识的方法;以上海大学“精海3号”无人水面艇为对象进行了模型参数辨识实验,并设计了基于规则表的模糊控制算法,仿真和实验验证了中速和高速下所辨识模型的正确性.

1 无人水面艇操纵模型

1.1 运动学建模

由于无人水面艇工作于水面,如果忽略地球曲率影响则可以近似看作平面运动,因此通常使用三自由度平面运动模型来表征无人水面艇的水面航行状态(见图1)[7],三自由度平面坐标为η[x,y,ψ]T∈R3,船体坐标系速度向量为v[u,v,r]R∈R3,其中x、y、ψ分别表示为船体在世界坐标系下的坐标和相对正北的艏向角;u、v、r分别为艇体右舷向、前向速度以及转艏角速度.

在上述简化配置空间里,北-东-地坐标系下的速度和船体坐标系下的速度转换关系可以表示为

式中:

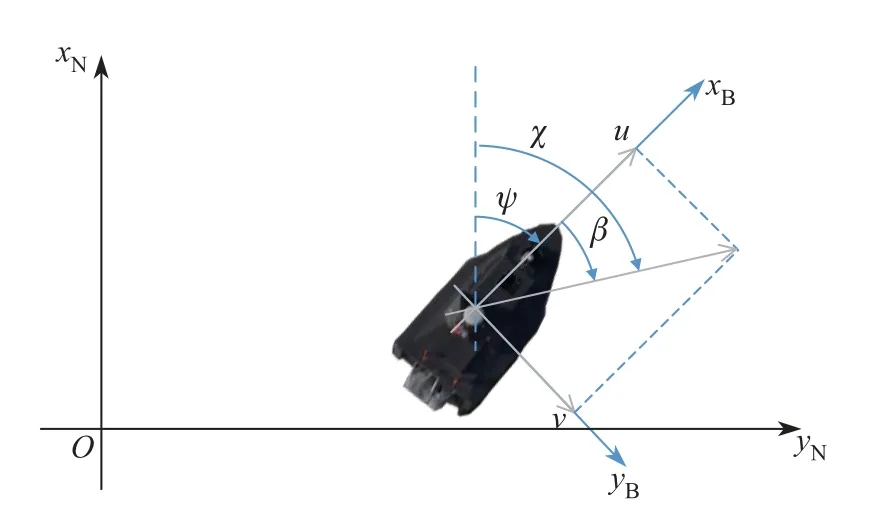
图1 无人水面艇平面运动坐标系Fig.1 Plane motion coordinate system of USV

1.2 动力学建模

在船舶操纵过程中,艏向角ψ和艏向角速度r与舵角δ之间的关系是船舶操纵模型[17],即船舶转艏动力学模型:

式中:T1、T2为时间常数;K为比例因子.方程(2)也被称为2阶线性KT方程,该方程描述了操舵对船舶转艏的影响.

2 系统辨识

无人水面艇操纵模型的构建通常有2种方法:①采用数值计算的方法,通过拖曳实验配合计算流体动力学(computational fluid dynamics,CFD)[18-19]软件计算获得系统模型,这种方法的缺点是需要大量实验才能获得完整的动力学因子;②基于获得的期望模型的输入输出实验数据,通过系统辨识处理获得系统模型,该方法的缺点是获得的模型只在实验状态下有效,而优点是简单快速,可以较快获得无人水面艇模型,加快控制算法设计速度.本工作采用第2种方法,通过对系统进行2级辨识得到系统的操纵模型.

2.1 系统辨识方案

无人水面艇运动控制系统的输入为舵角值,控制输出为艏向角速度,其控制过程包含2个阶段:①舵角通过液压执行器控制系统输出实际舵角值,此阶段受航速影响较小;②艇体运动系统输出艏向角速度,此阶段和无人水面艇航速高度耦合,需要辨识不同速度下的转艏模型(见图2).

图2 系统辨识方案Fig.2 System identification scheme

采用如图2所示的辨识方案,第一级为辨识液压转舵系统模型,第二级为辨识艇体转艏运动系统模型.由于艇体动力学模型参数受环境影响较大,因此在不同海况下辨识出来的模型存在较大差异.

本工作采用如式(3)所示的符合度Fit来评价模型的辨识精度[20]:

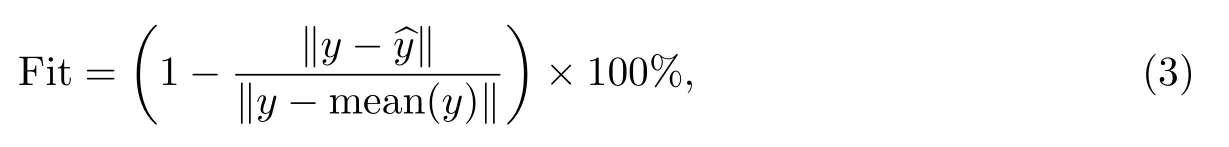
式中:y为船体实际输出值;^y为对应的模型输出值;mean(y)为实际输出值的平均值.通过此定义可以看出,模型符合度越高,Fit值越接近于100%.

本系统辨识以上海大学“精海3号”无人水面艇[21-22]为研究对象(见图3),该无人水面艇是小型无人测量艇,其设计参数如表1所示.在本次辨识过程中,风力为偏北风1 m/s,1级海况,浪高0～30 cm.

图3 “精海3号”无人水面艇Fig.3“Jinghai 3”unmanned surface vehicle

表1 艇体参数Table 1 Vehicle parameters

2.2 液压转舵系统辨识

液压转舵系统辨识的输入是舵角命令值,输出是舵角实际值,数据采集时间为100 s,采集频率为10 Hz.

辨识采用的输入输出数据如图4所示,辨识时采用的模型分别为1、2、3阶线性传递函数模型,其辨识结果如图5所示.

图4 液压转舵系统输入输出Fig.4 Input/output of hydraulic steering system

图5 液压转舵系统辨识结果Fig.5 Identification results of hydraulic steering system

表2为液压操舵辨识结果.从辨识结果可以看出,1阶传递函数的符合度最低,为70.1%;当使用2阶系统辨识时,符合度提高到86.89%;当使用3阶系统辨识时,符合度相较于2阶系统略有提高,为88.09%.考虑到系统阶次越高复杂度就越大,故采用2阶传递函数描述液压转舵系统:

式中:δ为舵角;s为拉普拉斯变量.

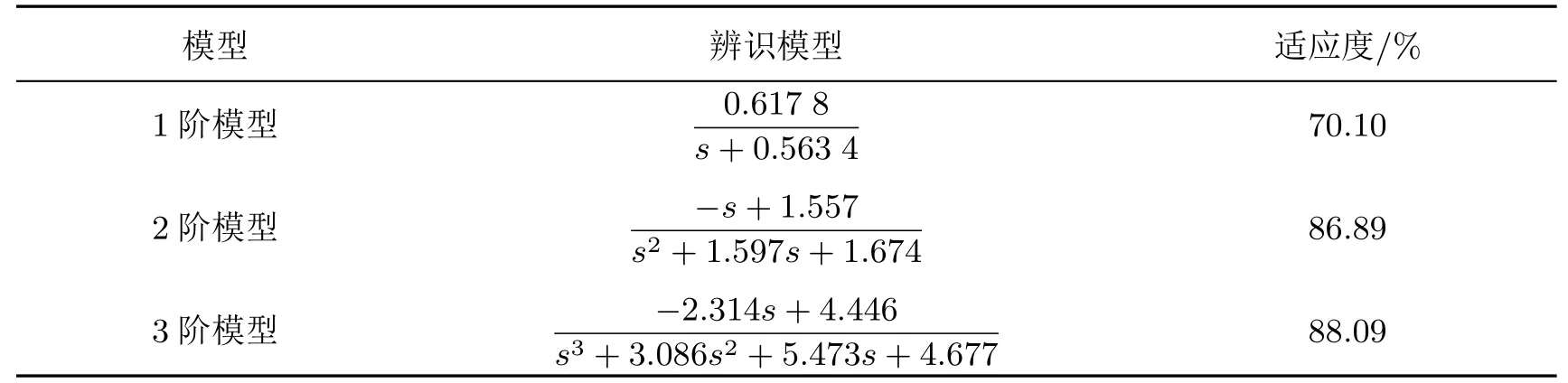
表2 液压操舵系统辨识结果Table 2 Identification results of hydraulic steering system

2.3 转艏系统辨识

艇体运动系统辨识是该辨识架构的第二级辨识,辨识的是艏向角速度对应于实际舵角的模型.与舵角控制系统不同,艇体运动系统对环境较敏感,辨识结果受速度、海况等的影响较大.为此,本工作以速度区间进行分级,分别辨识了怠速(1～2节)、中速(7～9节)、高速(13～15节)下的转艏模型.

2.3.1 高速转艏辨识

辨识的输入是舵角实际值,输出是转艏角速度,数据采集时间为100 s,采集频率10 Hz,输入输出情况如图6所示.

图6 高速转艏系统辨识输入输出Fig.6 Input/output of high speed heading model identification system

转艏系统辨识分别采用了2阶传递函数模型、4阶ARX自回归各态历经(autoregressive exogenous,ARX)模型和非线性ARX模型,辨识结果如图7所示.

图7 高速转艏系统辨识结果Fig.7 Identification results of high speed heading system

表3 高速转艏系统辨识结果Table 3 Identification results of high speed heading system

从辨识结果可以看出,在高速状态下2阶传递函数模型符合度最高,故转艏系统模型采用2阶传递函数模型:

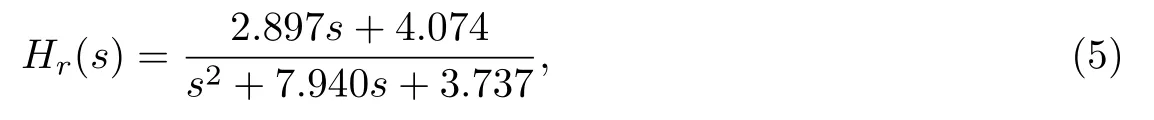
式中:r为艏向角速度.

2.3.2 中速和怠速转艏模型辨识

中速、怠速辨识过程和高速一致,为了保证系统的一致性,本工作均采用2阶传递函数模型,结果如表4所示.

表4 中速和怠速的辨识结果Table 4 Identification results of medium and low speed

从中速和怠速的辨识结果可以看出,在中速下获得的模型符合度可以达到76.76%,但是在怠速下模型符合度只有26.14%,说明在怠速下舵效较差,即在怠速下无法有效控制艏向,因此在后续仿真和实验中不对怠速进行讨论.

3 仿真及实验验证

本系统仿真过程如图8所示.图中,仿真输入是期望艏向角,控制器采用基于规则表的模糊PD控制器,舵角模型和转艏模型采用第2节辨识得到的模型,再通过积分器得到艏向角信息.这里,ψd为期望艏向角.

图8 仿真框图Fig.8 Simulation scheme

3.1 控制器

本控制器基于规则表的模糊PD控制器,控制器原理如图9所示.输入信息分别为艏向误差e和误差变化量Δe,模糊化后采用乘积推理,最后利用中心平均解模糊器进行解模糊.

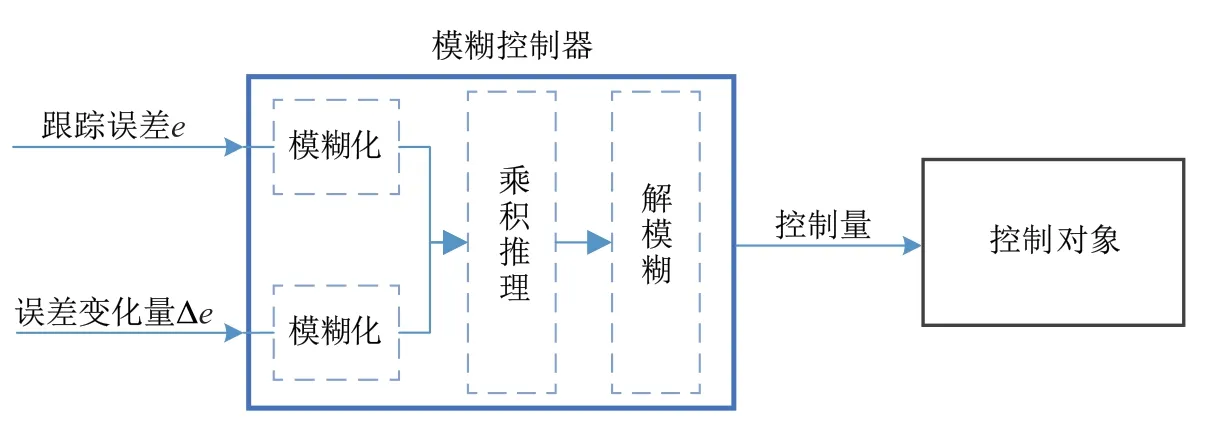
图9 模糊控制器Fig.9 Fuzzy controller

模糊化隶属度函数为

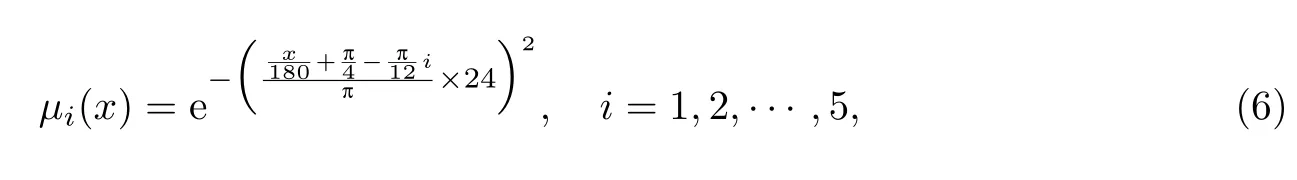
乘积推理

采用中心平均解模糊器进行反模糊化,得到模糊控制器

式中:uij为规则表值.模糊规则表如表5所示.

表5 uij模糊规则值表Table 5 Table of uij fuzzy rule values

3.2 仿真结果分析

分别对本系统进行镇定仿真和跟踪仿真.其中,艏向镇定仿真是仿真无人水面艇在高速/中速、零初始条件下的受迫响应,艏向跟踪仿真是测试零初始条件下的正弦信号激励的响应.

3.2.1 艏向镇定仿真

仿真设定初始艏向角为0◦;输入期望艏向角90◦;仿真时间100 s;采样频率10 Hz.仿真结果如图10和11所示,定量分析结果如表6所示.

图10 高速艏向镇定仿真Fig.10 High speed heading keeping simulation

图11 中速艏向镇定仿真Fig.11 Medium speed heading keeping simulation

表6 艏向镇定仿真结果Table 6 Heading keeping simulation result

通过仿真实验可以得到:在高速下当s期望艏向为90◦时,上升时间tr为10.5 s,5%标准调整时间ts为23.1 s,最大超调量Mp为7.5%,静态偏差e∞为-2.32,控制器输出的控制量稳定在0◦,艏向偏差稳定在-2.32◦;在中速下,系统的上升时间tr为11.3 s,调整时间ts为30 s,最大超调量Mp为25.4%,静态偏差e∞为-2.3,控制量收敛到0◦.

从高速和中速的艏向镇定仿真可以看出,高速和中速状态下无人水面艇均可以成功实现艏向镇定.高速情况下上升时间、调整时间和超调量均最小;中速情况下调整时间较高速情况下增加了6.9 s,超调量达到了25.4%.上升时间和调整时间均快于中速镇定,而且超调量高速状态远低于中速状态,静态误差相似.由于速度越快,无人水面艇的转艏响应越快,因此高速情况优于中速情况,仿真结果符合无人水面艇的实际情况.由于静态误差时控制算法没有引入积分控制,故无法消除静态误差,和模型无关.

3.2.2 艏向跟踪仿真

艏向跟踪仿真是仿真系统在零初始条件下在正弦信号激励下的响应行为.本实验仿真的正弦信号为幅值90,频率0.02π,周期100 s;仿真时间为100 s,即进行一个周期的仿真,系统采样频率10 Hz.仿真结果如图12和13所示,定量分析如表7所示.

图12 高速艏向跟踪仿真Fig.12 High speed heading tracking simulation

从艏向跟踪仿真结果分析可以看出:在高速和中速状态下都可以对艏向进行跟踪.高速时,输出艏向角能够完全跟踪正弦输入信号,信号平均延迟4.7 s,峰值衰减3.8%;中速时,在一个正弦周期内,输出艏向角能够完全跟踪正弦输入信号,信号平均延迟4.3 s,峰值无衰减.这里,二者的跟踪延迟时间平均在4.7 s和4.3 s,说明在高速和中速状态下,该模型的跟踪性能相差不大.

3.3 实验

艏向控制实验是通过实际海测来验证控制系统的性能,也通过实际测量来检验基于规则表的模糊PD算法的控制性能.实验海况1～2级,浪高约30 cm,偏北风1～5 m/s.在实验中,目标艏向为90◦,实验时间100 s,采样频率10 Hz,实验结果如图14、15所示,定量分析如表8所示.

图13 中速艏向跟踪仿真Fig.13 Medium speed heading tracking simulation

表7 艏向跟踪仿真结果Table 7 Heading tracking simulation results

图14 高速艏向控制实验Fig.14 High speed heading control experiment

通过实验分析可以看出,在控制开始后,艇体艏向能够快速向目标艏向转动,并且最终能够在目标艏向附近震荡,这里,震荡是由于无人水面艇在海里运动时,会受到不确定的风、浪、流的影响,这些外界的力作用于无人水面艇上会使其艏向偏离,通过算法控制将艏向纠正,所以实验数据中会发现艏向角是不收敛的,而是在目标艏向上下震荡,在实际运行过程中,当艏向在正负10◦以内震荡时,船体仍然可以保持良好的直线运行.由于实验时无法准确控制起始角度,在目标角度都是90◦的情况下,高速起始角度0◦,而中速起始角度52◦,通过比较上升时间和调整时间可以发现,高速的艏向控制效果优于中速时的情况,且和仿真结果一致,说明该模型可以反映系统性能.但是比较绝对时间可以看到,仿真和实验结果还是差异较大,这一方面来自于模型和实际有部分偏差,另一方面是由于实验时的海况和风况在辨识时有区别.

图15 中速艏向控制实验Fig.15 Medium speed heading control experiment

表8 艏向控制实验结果Table 8 Heading control experiment result

4 结束语

本工作采用分级辨识的方法分别得到了无人水面艇操舵系统和转艏系统的模型,且为了获得不同速度下的转艏模型,分别在高速、中速和怠速下进行了转艏模型辨识,通过对比得到了2阶传递函数模型,通过仿真和实验分析得出该模型可以在一定程度上反映无人水面艇的真实情况.因此,分级辨识方法可以快速应用于无人水面艇控制系统的设计和改进,是无人水面艇快速工程化的一个有效方法.后续工作将在此模型辨识的基础上,研究模型预测算法、反步法模型控制算法的设计和改进.