基于数学历史的勾股定理教学设计
李织兰 肖宝莹 沈洁 蒋晓云


【摘要】本文在解读课标和分析教材及有关勾股定理教学文献的基础上,阐述勾股定理教学设计,即以历史故事为引子,带领学生初识勾股定理,让学生通过实验归纳发现勾股定理,并了解“出入相补,无字证明”的方法,以培养学生科学精神和数学核心素养。
【关键词】勾股定理 科学精神 数学历史 核心素养
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2021)33-0149-04
勾股定理是数学发展史上一颗璀璨的明珠,只要说到勾股定理,我们总会想到“商高”“勾三股四弦五”“毕达哥拉斯”“赵爽弦图”“出入相补”等,在勾股定理的研究历程中彰显了古今中外研究者的数学精神。其证明方法也极其多样化,体现了各国数学家孜孜不倦的钻研精神。勾股定理是数学发展的重要根基之一,它不仅被认为是平面几何中最重要的定理之一,也被认为是数学中最重要的定理之一。勾股定理是初中数学课程的核心内容之一,历来是教学改革的风向标。
一、课标解读与教材分析
《义务教育数学课程标准(2011年版)》强调了数学文化在课程中的价值,指出在人类文化中数学文化占据着重要位置,并要求在数学课程的教学中适当融入数学文化。
勾股定理用中文表达是,直角三角形的斜边的平方等两直角边的平方和;用数学语言来表达是,如果直角三角形的两直角边分别为a和b,斜边为c,那么c2=a2+b2。
它揭示了直角三角形三边之间的数量关系,体现了数形结合的思想方法。勾股定理启发了人类对数学的深入思考,促成了三角学、解析几何学的建立,为数学的进一步发展拓宽了道路。因此,勾股定理和黄金分割被誉为“几何双宝”,前者好似珠玉,后者堪称黄金。本节课选自人教版初中数学八年级下册第18章第1节《勾股定理》的内容。课文以发现和证明勾股定理的各种几何方法为主线。在此基础上,我们梳理了发现和证明勾股定理的历史过程,从而决定以勾股定理发展的历史文化背景为暗线。在这两条线上设计课堂教学过程,并将两条线贯穿整堂课的始终。目的是借助勾股定理丰富的文化背景,培养学生科学精神。几千年来,在勾股定理探索的过程中,一代代人皓首穷经,不断积累,才挖掘出数学中的这一珍宝。数学大师们在生活中发现和思考,不懈地探索,找到了一个个精妙的解决直角三角形的方法,并将勾股定理的发现和思想方法推向一个又一个新领域。它拥有无穷的奥秘,亟待我们去探索、去追寻。我们要学习数学家刻苦钻研的精神,不断探索数学的奥秘。在课堂上,我们可以沿着大师的足迹,经历发现勾股定理的过程,运用实验归纳方法体验从特殊到一般的归纳思想。在教学中,教师也可适当讲解数学界有关给勾股定理命名的历史。勾股定理的命名是一件令中华民族深感无奈和遗憾的事情。从这件事情上让学生思考,发现一个规律,或解决一个问题之后,去追求“更普遍的真理”“更一般的规律”是何等的重要。要培养良好习惯,具备科学的思维品质,培养数学精神。
我国古代数学赵爽用弦图证明勾股定理,是一种数形结合证法,它建立在一种不证自明、形象直观的原理上。他在证明过程中,借助图形使问题数学化。在课堂上,教师可介绍这种方法,让学生了解勾股定理的这一种证明过程,学会用“出入相补”的证明方法,体会数形结合思想。弘扬中国古代数学家辉煌成就,感悟古人的智慧,增强民族自豪感,培养爱国主义精神。
二、勾股定理教学文献分析
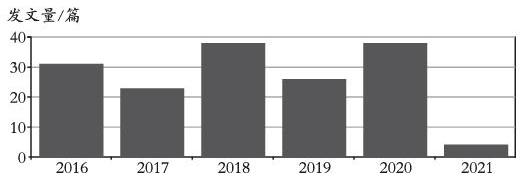
在CNKI按检索式“发表时间between(2016-04-01,2021-04-01)and主题=勾股定理教学”进行检索,检索到文献共161篇,从发文量可看出,勾股定理的教学研究是近年的研究热点问题之一。
为了借鉴优秀教学成果,通过对文献整理,从勾股定理的发现教学和勾股定理的证明教学这两个方面进行了教学分析。
(一)发现勾股定理的教学
多数文献是通过毕达哥拉斯参加聚会的故事,引导学生了解从探究等腰直角三角形,推广到一般的直角三角形,从而得到直角三角形三边之间的数量关系的研究方法。笔者主要参考以下几个人的文献:(1)郝金芝的文献,通过提问学生“如果两个特殊条件——‘等腰、直角’缺少其中一个条件,那么三角形还具有这样的性质吗?”添加条件或去掉条件,得到三个不同条件的直角三角形,再根据探究等腰直角三角形经验找到解决问题的方法。启发学生利用网格内正方形面积的方法进行探索,通过辨析、猜想、发现,最后得出结论。在这一过程中,通过添加或去掉条件进行研究,进而找到共性的这个过程很新颖,体现特殊到一般的归纳思想。(2)卢明一、张新然、曾泽群等人的文献,在讲述了毕达哥拉斯故事后,引导学生通过研究面积关系,并将之转化为三边关系,从而发现等腰直角三角形的性质。在此基础上,探究普通直角三角形的性质。利用正方形面积的关系,利用割补的方法求出以直角三角形的斜边为边建立正方形,得到的面积与两直角边对应的正文形的面积的关系,从而发现直角三角形的三边的关系——勾股定理。这个过程是一个探究式的学习过程,让学生体验从特殊到一般的过程。在这个过程中,培养学生归纳的思想,体现数学史的教育价值。
(二)证明勾股定理的教学
证明勾股定理的方法很多,绝大多数教学研究文献通过渗透数学史、融入数学文化等途径,让学生了解勾股定理的证明过程,循大师足迹,悟数学文化,培养数学精神。笔者主要参考以下几个人的文献:(1)郝金芝,引导学生将任意的直角三角形放入网格中,观察顶点是否在格点上。如果在,那么就可利用三边的特殊性求解三边的关系;若不在,那么应该怎么去求三边之间的关系?让学生借鉴之前利用网格发现勾股定理的研究思路,通过图形拼接,进行一般性证明。(2)赵爽,利用弦图法,对图形进行拼、割,然后利用面积法证明。这个证明过程比较严谨,值得学习。这些文献資料阐述的证明勾股定理的方法,比较注重数学史的传承问题,旨在使读者感受古人的智慧。(3)卢明一,向学生讲述赵爽弦图的方法,通过幻灯片将整个拼摆过程动态地展现,让学生直观地看到证法的整个过程。然后利用几何画板演示直角三角形,改变三边长度,发现其三边关系保持不变,从而证实勾股定理。在这整个过程中,让学生动手实践,观看利用赵爽弦图证明勾股定理的视频,然后利用信息技术对证明过程进行验证。这样既能加深对勾股定理的理解,又能体会我国古人智慧,让学生感受数学文化。(4)张新然,以四个全等的直角三角形为研究对象,让学生动手拼摆,当摆到与赵爽弦图一样时,再利用几何画板为学生演示。这种教学活动可培养学生动手能力,感受数形结合思想。
这些文献的教学设想和方法值得我们借鉴,而如何充分发挥勾股定理的文化价值和教育价值仍需进一步思考。
三、基于数学历史的勾股定理教学设计
在教学中,教师基于自身的教学视野、数学理解能力、数学史功底,精心教学设计,让学生沿着历代数学大师的足迹,复现数学大师的思维过程,使之得到启迪;进而使学生能够根据自己的体验,用自己的思维方式,“再创造”数学,形成科学精神。结合教材内容和教学目标,笔者安排本课的教学流程如下:
(一)历史故事,初识定理
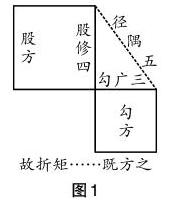
在我国古代,人们将直角三角形中短的直角边叫做勾,长的直角边叫做股,斜边叫做弦。3000多年前,中国古代人们已经知道,如果勾是三,股是四,那么弦是五(如图1所示)。这是商高发现的经过后人进一步证明了的勾股定理中的一个特殊例子,但特例以外还有无穷个直角三角形不能用“勾三股四弦五”来求解。
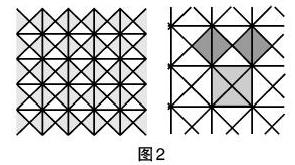
相传2500年前,有一次,毕达哥拉斯到朋友家中做客,他在欣赏镶嵌在地面上美丽的地砖时,发现它们和“数”之间的关系:两个小正方形的面积的和等于这个大边长正方形的面积,这是等腰直角三角形的一个性质(如图2所示)。毕达哥拉斯发现等腰直角三角形的这一特殊性质之后,他还研究了很多不同类型的直角三角形,归纳发现:任意直角三角形两直角边的平方和等于斜边的平方。让学生跟随毕达哥拉斯的脚步,一起来做实验,探究一般的直角三角形的三边数量关系。
【设计意图】介绍勾股定理的历史起点,并将之当作本节课暗线的起点。借助教材的章前图文激发学生的学习兴趣。让学生体悟从特殊到一般的研究问题的思想。
(二)实验归纳,发现定理
毕达哥拉斯发现等腰直角三角形这一特殊性之后,他继续思考:对一般直角三角形是不是也存在这样的“三边”的数量关系呢?
三个正方形的面积,实际也分别是对应直角三角形的三条边的平方,从而获得一个关于直角三角形性质的初步结论:两直角边的平方和等于斜边的平方。从特殊的现象中提出问题。
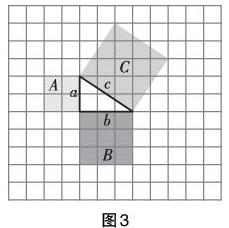
学生活动1:在方格纸上画出任意直角三角形,分别以三边向外作三个正方形,通过割或补的方法计算各正方形的面积,验证三边的平方关系。(如图3所示)
【设计意图】此时直接让学生去证明三边的平方关系,难度很大,为了降低学生的思考难度,教师及时引导,回到课堂开始的图形,直接提示学生借助方格纸作图,利用面积的割或者补的方法得到边长的平方关系。以此打开教学,突破难点。
学生在网络方格纸上独立画直角三角形,并利用网络方格验证直角三角形三边的平方关系。绝大部分同学都能以直角三角形的三边分别向外作了三个正方形,通过计算正方形的面积来验证三边的平方关系。这个过程涉及求方格纸中斜放的正方形的面积问题,这是难点。请两位同学展示他们不同的验证方法。
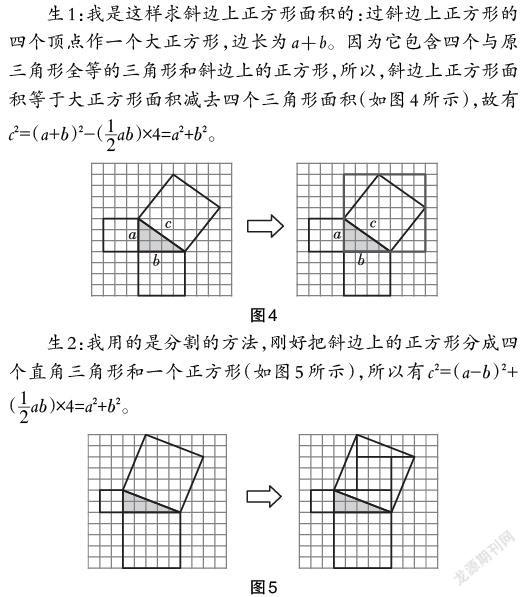
生1:我是这样求斜边上正方形面积的:过斜边上正方形的四个顶点作一个大正方形,边长为a+b。因为它包含四个与原三角形全等的三角形和斜边上的正方形,所以,斜边上正方形面积等于大正方形面积减去四个三角形面积(如图4所示),故有c 2=(a+b)2-([12]a b)[×]4=a2+b2。
生2:我用的是分割的方法,刚好把斜边上的正方形分成四个直角三角形和一个正方形(如图5所示),所以有c 2=(a-b)2+([12]a b)[×]4=a2+b2。
师:无论是“割”还是“补”的方法,都是用不同的方法把同一个正方形表示,这种构造法是证明问题的一种思路。
追问1:我们在方格纸中任意作的一个顶点在格点上的直角三角形,都能验证两直角边的平方和等于斜边的平方,但我们能不能说,对所有的直角三角形,三边都满足这样的关系?
追问2:如果我们把方格纸去掉,会对他们的证明有实质的影响吗?
实验验证还不能算严格的证明,因为方格纸具有特殊性,实验归纳得到的结论可能是正确的,也可能是错误的。想要获得一般性的结论,需要在一般的平面上对一般的直角三角形进行证明。
【设计意图】让学生在方格纸上作图以进一步验证结果,即用割或者补的方法验证两个小正方形的面积之和等于大正方形的面积。在此过程中,让学生进一步感知猜想的正确性,巩固常用的割或补求面积的方法,从而使学生体会从特殊到一般的思想,思考并理解怎样才能使问题一般化;理解把一个问题一般化的方式——用字母表示数,理解通过代数式的化简得到一般的结论的过程。在不断追问中使学生初步感受构造法是数学证明的一种思路,为赵爽弦图证明勾股定理作铺垫。
(三)出入相补,无字证明
数学以其严谨、严密、客观,使人们对其敬畏和信任。数学是求真的,它不轻信实验、观察、归纳。在实践中发现的数学结论必须经受极为严格的逻辑检验(即数学证明),才能成为定理。
约在222年赵爽创作了一篇“勾股圆方圆说”论文,他画了一张“弦图”表述勾股定理,并给出了一个绝妙的证明:“勾股各自乘,并之为弦实,开方除之即弦。案:弦图又可以勾股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实,加差实,亦成弦实。”(如图6所示)
赵爽弦图的证明思路:每一个直角三角形称为“朱实”,中间的一个正方形称为“中黄实”,以弦为边的大正方形叫做“弦实”。
趙爽将“勾股定理”一般化才形成了真正的勾股定理,其证明过程有图为证,永载史册。赵爽证明勾股定理的这个方法可谓精妙绝伦,为将代数和几何紧密结合,使之互不可分的一个典范,这个无字证明(不用数学语言证明,如图7)的方法被哈佛大学教授库里奇称为“最省力的证明”。正因为此,“赵爽弦图”被选为2002年国际数学家大会会徽,现在这个标志也成了中国数学会的标志。(如图8所示)
刘徽为《九章算术》勾股数——“勾股各自乘,并而开方除之,即弦”所作的注:“勾自乘为朱方,股自乘为青方,令出入相补,各从其类,因就其余不动也,合成弦方之幂,开方除之,即弦也。”
如何将勾方与股方出入相补成弦方?教师进一步介绍数学家刘徽的“青朱出入图”。(如图9所示)
刘徽把“赵爽弦图”和“青朱出入图”所蕴含的思想方法总结为“出入相补”原理。“青朱出入图”巧妙地利用了“出入相补”原理,且蕴含动态思想,具有科学创新的意义。
【设计意图】介绍中国古代数学家证明勾股定理的方法——赵爽弦图法,使学生了解我国古代数学家对探索勾股定理作出的贡献,知道他们是我国古代数学的骄傲。感悟古人的智慧,增强民族自豪感,培养爱国主义精神。介绍勾股定理发展的一个历史线,回看古人数学成就,彰显古今中外数学精神,培养学生的良好习惯和思维品质,培养学生的数学精神。
(四)数学文化,科学精神
公元前3000年,古巴比伦人就知道了很多组的勾股数,而且留下了实物证据——记满勾股数的泥板。商高“勾三股四弦五”比毕达哥拉斯发现勾股定理至少要早500年,因此,一些过去的教科书中讲是中国人商高最早提出了这个定理,于是称之为勾股定理或者是商高定理。但课文说:“在西方,一般认为这个定理由毕达哥拉斯发现的。”这是为什么?
古代巴比伦的数学泥板书没有形成数学理论,泥板书上的数学也因带有推测的成分故而存在争议。《周髀算经》中的“勾三股四弦五”只是记载了一组勾股数,是后人进一步证明了的定理中的一个特殊例子,并不能说明发现了任意直角三角形三边的数量关系的规律,特例以外还有无穷个直角三角形不能用“勾三股四弦五”来求解。一个结论要成为定理,需要做出一个一般性的描述。这个描述可以把它称为命题,命题经过严格的逻辑检验(数学证明)才能成为定理。反思中国古代数学家没有去探究“更一般的规律”,因此几千年来,西方国家一直称“直角三角形两直角边的平方之和等于斜边的平方”这一定理为“毕达哥拉斯定理”而不是“商高定理”或“勾股定理”。尽管2002年在北京召开的世界数学家大会把证明勾股定理的赵爽弦图设计成会徽悬挂在会场,以彰显中国古代数学家在探索勾股定理的过程中的独特贡献和地位,但国际数学界仍然把勾股定理命名为“毕达哥拉斯定理”,勾股定理的命名成了一件令中华民族深感无奈和遗憾的事情。在教学中,教师可通过这件事情让学生懂得:发现一个规律或解决一个问题之后去追求“更普遍的真理”“更一般的规律”是何等的重要,因此要养成良好习惯,要有科學的思维品质,培养数学精神。
【设计意图】使学生充分地感受整个数学的发展史就是人类物质文明和精神文明的发展史。求真是数学教育的最高境界,是我们的追求。数学文化绵延古今,经久不息,我们要传承数学精神。
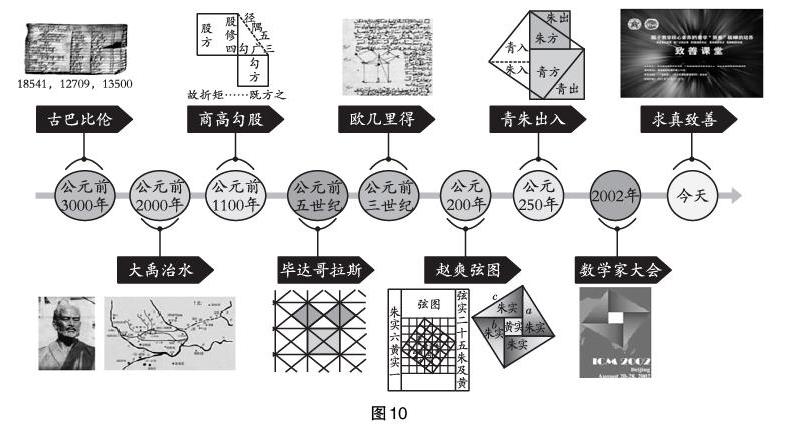
勾股定理是初中数学课程的核心内容之一,历来是教学改革的风向标。勾股定理的研究过程彰显了古今中外研究者的数学精神。本课例选自人教版初中数学《勾股定理》的内容,以发现和证明勾股定理的各种几何方法为主线,梳理勾股定理发展的历史线;以勾股定理发展的历史文化背景为暗线,并将之贯穿整堂课的始终(如图10所示)。在教学过程中,利用勾股定理丰富的文化背景,培养学生科学精神。
【参考文献】
[1]蒋晓云.文化视角下的小学数学课例研究[J].广西教育,2018(1).
[2]郝金芝.“勾股定理”教学设计[J].中国数学教育,2020(11).
[3]卢明一,李碧荣.基于数学史的勾股定理教学设计[J].广西教育,2019(29).
[4]张新然.“勾股定理”教学设计及两点思考[J].中国数学教育,2019(Z3).
[5]曾泽群,赖宝禧.HPM视角下的“勾股定理”教学设计[J].数学教学,2019(9).
[6]张冬莉,代钦.毕达哥拉斯定理证明2500年的文化史趣谈——以E.S.Loomis的《Pythagorean Proposition》为例[J].数学通报,2020,59(2).
[7]俞求是.《周髀算经》“周公商高问答”相关问题的研究[J].数学通报,2019,58(2).
注:2020年度广西基础教育改革发展研究中心课题:基于核心素养的数学“致善”精神的培养策略研究(课题编号GSJJB202005);广西教育科学“十三五”规划2019年度重点课题:小学数学教学中学生“科学精神”的培育研究(课题编号2019B141)。通讯作者:蒋晓云。
(责编 李 唐)

