基于光度曲线的弱特征空间目标姿态估计
梁勇奇,韩凌峰,李恒年
(1. 西安交通大学机械结构强度与振动国家重点实验室,西安 710049;. 西安卫星测控中心宇航动力学国家重点实验室,西安 710043)
0 引 言
随着近年来空间目标数量的增加,使得对空间态势感知的需求越来越高。对于距离远、尺寸小的空间目标,雷达受到其功率的限制以及观测噪声的影响难以成为有效的观测工具,作为另一种重要手段光学观测难以对此类目标成像,通常仅能得到反映亮度变化的光度曲线。由于光度观测数据与目标在空间的相对位置、姿态、目标形状、材料特性等特征都有关系[1],通过光度数据获取空间目标的运动信息与特征信息的途径受到重视。
传统上基于光度观测的研究主要通过反演的方法获得目标的动态信息或者特征信息[2-3],这种离线处理的途径获取的有关目标的信息通常有限,而且离线处理会影响到飞行器动态信息获取的实时性。近年来在国际上兴起采用递推滤波技术实时获取空间目标运动信息与特征信息的研究。文献[4]发展了适用于空间目标姿态估计的无味滤波器(Unscented filter,UF),使用该滤波器文献[5]首次在光度观测下实现对处于垂直于轴线方向翻滚的火箭发动机圆柱体残骸的姿态估计。通过多模型方法文献[6]使用姿态运动学模型与轨道动力学模型实现对常见空间目标的尺寸识别与状态估计。通过姿态动力学模型与轨道动力学模型文献[7]进一步实现对这些空间目标的形状、尺寸的识别以及状态的估计。文献[8]建立外形不确定性的一阶动力学模型并采用粒子滤波器(Particle filter,PF)实现空间目标姿态快变过程中的姿态角估计。本课题组在文献[1]中分析了典型的正四棱柱、正六棱柱和正八棱柱空间目标的形状对姿态估计的影响,并探讨了算法对姿态随机缓慢机动目标的自适应跟踪能力。文献[9]尝试使用深度卷积神经网络实现对光度曲线特征差别显著的几类目标的分类。
从上述分析看出,基于光度曲线研究方法的优点在于不受限于目标的轨道高度,其有效工作的前提是能够检测到目标的光度信息,但是当前研究局限于开展对具体对象的跟踪与识别,其结果受到目标多样性的影响,所关注的主要问题是自旋对象在太阳照射下产生具有显著波动特征的光度曲线,而未对光度曲线波动不明显的对象予以关注。文献[1]中发现,在进行目标姿态跟踪时,光度曲线波动不明显的正八棱柱目标相对于波动特征明显的正四棱柱目标,其姿态跟踪的误差增加且收敛速度变慢,这反映了对光度曲线波动不明显目标的姿态跟踪更难,本文开展对该类新特征对象的研究。
本文首先提出弱特征目标的概念并分析此类目标光度曲线的特征,进而提出基于多站联合观测的并行融合算法,并通过数值仿真分析站点间位置关系以及站点数量对姿态估计效果的影响。
1 问题的提出
选择具有相同角速度的正四棱柱、正八棱柱和正十二棱柱在同一时段通过同一站点进行光度观测,得到的光度曲线对比如图1所示。从图中看出,随着目标面数的增加,光度曲线相邻波峰与波谷的波动范围逐渐减小。根据文献[1]的结论,随着目标侧面数的增多,姿态估计误差增加,且收敛速度变慢,由此表明随着光度曲线波动范围的减小,目标姿态估计的困难相应增加。在存在角速度的情况下,我们将正十二棱柱这类光度曲线波动不明显的对象称作弱特征目标,而如何实现弱特征空间目标的姿态估计是有待于解决的问题。
为进一步揭示图1中正十二棱柱目标光度曲线特点,我们设置多个不同位置的观测站,并在同一时段对该目标进行观测,所得到的光度曲线如图2所示,从图中看出,不同站点得到的光度曲线共同特征是波动范围仍然都很小,但是它们之间差异明显,这些曲线间的差异对本文的研究带来启发。
2 基于多站联合观测的并行融合方法
图2中各观测站获得的光度曲线之间存在差异,意味着它们所包含的信息有差异。对于正十二棱柱这类弱特征目标,由于从单个观测站的光度曲线中获取的有关目标的信息很有限,若使用多个站点进行观测,就可以同时获取更多与目标有关的信息。

图1 不同形状目标的光度曲线对比

图2 不同观测站获得的正十二棱柱目标光度曲线对比
通过上述分析的启发,本文提出以空间换取精度的设想,通过在物理空间上分散布置站点,由于在不同站点对目标观测的视角不同,在这样不同视角下获取的目标信息也不同,并具有相互补偿的作用。通过对不同视角观测信息的综合利用,以实现对目标姿态的有效估计。
基于上述设想提出基于多站联合观测的并行融合方法,通过设置多个站点对目标进行多站同步光度观测,以探讨对弱特征目标姿态估计的可行性与有效性。该方法对于观测站点的布置没有特定要求,可以通过地基观测,也可以采用天基观测的方式。
2.1 多站联合光度观测建模
本文涉及的光度观测系统由太阳、空间目标、地面观测站三者构成,光度观测模型主要受到太阳、地球、空间目标三者的相对位置关系以及空间目标的姿态、形状、尺寸、表面材料属性等因素的影响。其中,太阳、地球和空间目标三者之间位置关系是建立光度观测模型的基础,如图3所示。从图中看出,如果站点位置不同,光度观测的空间几何关系会有差异,而站点之间的相对位置以及站点与空间目标之间的相对位置都会影响到观测效果。

图3 太阳、地球、卫星三者位置关系[1]
2.1.1光度观测模型
每个空间目标都可以看成是由N个平面构成的,观测站测到的光度大小为各个面反射到地面观测站光度大小的总和。光度计算模型为
(1)
式中:mapp为目标视星等;Csun,vis=455 W/m2为可见光照射到目标表面单位面积上的功率;Fobs(i)为太阳光线经目标表面i反射到地面观测站的辐射量,即
(2)

(3)
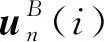
(4)

2.1.2多站联合光度观测模型
多站联合观测下同一时刻会从多个站点观测到光度数据,为便于表达及使用,我们给出观测模型
(5)
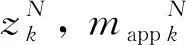
2.2 目标姿态运动学建模
目标状态向量为X=[θ1,θ2,θ3,ω1,ω2,ω3]T,其中θ1,θ2,θ3分别对应滚转角、俯仰角、偏航角,ω1,ω2,ω3为它们各自的角速度。用四元数表示目标姿态q=[ρT,q4]T,其中ρ=[q1,q2,q3]T,且qTq=1,则姿态和角速度的运动模型为
(6)
(7)

为解决四元数的乘性特性和规范化限制问题[4],引入广义罗德里格斯参数(GRPs),则目标姿态估计器的状态向量可表示为X=[δpT,ωT]T,姿态角与角速度联合估计的离散化动态模型为
X(k+1)=FX(k)+Γk
(8)

2.3 四元数无味滤波器
考虑到空间目标运动学模型、光度量测模型的非线性及四元数的特殊性,本文在算法实现的时综合了文献[6,11]所使用的UF进行姿态与角速度估计。
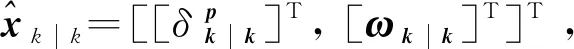

将状态的sigma点拆分为分别对应于GRPs和角速度的两部分
(9)
(10)
(11)
式中:四元数乘法q⊗p=[Ξ(p)p]q。
通过将χk(i)代入动态模型得到包含四元数的状态sigma点的一步预测
(12)
(13)
(14)
式中:四元数求逆q-1=[-ρT,q4]T。则包含GRPs的状态sigma点一步预测为
(15)


2.4 基于多站联合观测的并行融合方法
多站联合观测的数据处理涉及估计融合算法,目前的估计融合算法都与融合结构密切相关,融合结构大致分成三类:集中式、分布式和混合式。在集中式融合处理结构中,融合中心可使用所有传感器的原始量测数据,没有任何信息损失,融合结果是最优的,因此本文选择集中式融合系统进行数据处理。常见的集中式融合算法有三种:并行滤波、序贯滤波和数据压缩滤波,本文选择其中操作较为简便的并行滤波算法。并行滤波结构简单来说就是量测扩维,将扩维后的量测向量整体送入滤波器[12]。
根据上述分析需要进一步发展2.3小节的UF算法,本文算法与2.3小节的不同之处在于观测模型,为此重新设计了观测值的一步预测与状态的更新。
(16)
(17)
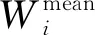
若采用N个地面观测站,将式(12)中包含四元数的状态sigma点一步预测χk+1(i)代入式(5)观测模型获得观测值的一步预测
(18)
则N个地面站观测值的预测均值和协方差为
(19)
(20)
状态和观测值的互协方差和增益分别计算为
(21)
(22)
若已知k+1时刻各观测站的光度数据,则状态和状态协方差更新为
(23)
(24)
3 仿真校验
通过数值仿真验证本文针对弱特征目标所提多站联合观测方法的可行性与有效性,为了更客观地反映站点设置对估计结果的影响,此处分别考虑了站点间离、站点数量和站点相对目标方位三类因素。
以倾斜地球同步轨道(IGSO)卫星为跟踪目标,卫星轨道根数设置为:半长轴a=42166.3 km,偏心率e=0°,倾角i=30°,升交点赤经Ω=120°,近地点幅角ω=0°,平近地角M=0°;设定卫星为正十二棱柱,每个面的面积为60 m2,且镜面反射率和漫反射率都相同,分别为Rspec=0.5和Rdiff=0.4。
卫星轨道数据由卫星工具箱(STK)仿真得到,选择的跟踪时段为2015年5月22日05:00:00 UT到2015年5月22日07:00:00 UT。卫星运行时的星下点轨迹如图4所示,并在图中布置13个观测站点。根据经验选择站1为基础观测站,并相对该站在不同的方位上布置了其他12个站点作为对照。
卫星在初始时刻以四元数表示的姿态为q=[0.746057, -0.106878, -0.100389, 0.649537]T,角速度为ω=[0, 0, 8.65621]T(°)/min。
采用上文设计的UF,需要估计的目标状态为X=[θ1,θ2,θ3,ω1,,ω2,ω3]T,初始状态协方差P(0)=diag(0.1,0.1,0.1,(10-6)2,(10-6)2,(10-4)2),过程噪声协方差Q=diag((10-4)2, (10-4)2, (10-4)2, (10-13)2, (10-13)2, (10-5)2),每个观测站的光度观测噪声协方差为R=0.12。
为了综合比较姿态估计性能,我们给出姿态角均方根形式的误差评估指标
(25)


图4 卫星星下点轨迹及各观测站位置
3.1 不同站点获取的光度曲线间差异分析
为进一步分析第1部分所述的光度曲线特征,从图4中选择一些代表性站点对目标进行光度观测,所得到的光度曲线如图5所示。从图中看出,各站点观测到的光度曲线有差异,分别沿着站1的经线和纬线布置站点,光度曲线之间的差异随着观测站之间距离的增大而增大,如站5和站1所得到的光度曲线间的差异比站2和站1间的大;站9和站1所得到的光度曲线间的差异比站6和站1间的大。
沿卫星对太阳光线反射相同方向布置的站点所观测到的光度曲线差异较小,而沿卫星对太阳光线反射相反方向布置的站点观测到的光度曲线差异较大,如站10与站1所得到的光度曲线间的差异比站5和站1间的大;站11和站1所得到的光度曲线间的差异比站9和站1间的大。
从上述分析看出,分别沿着纬线方向和经线方向来看,光度曲线间差异受到站点间距离的影响;而沿着不同观测方位所布置站点之间观测曲线的差异变得更为复杂。作为观测量的光度曲线,其差异影响到姿态估计的收敛性和精度。除上述光度曲线之间的差异性,还需考虑到站点数量对多站融合估计的影响,下面我们分析在这些因素影响下本文所提出多站联合观测方案对弱特征目标姿态估计的能力,并探讨其中可能存在的规律性。
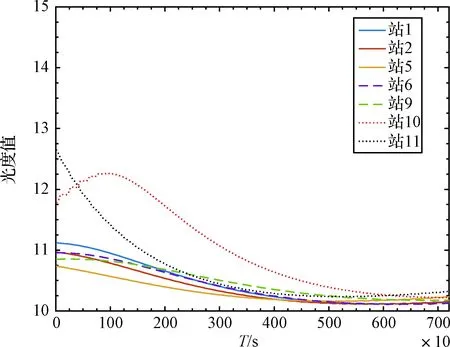
图5 不同观测站所获得光度曲线的对比
3.2 站点间距离对姿态估计的影响
3.2.1沿纬线方向设置站点
选择站1为基准站点,分别与站2、3、4、5组合,按照2.4节算法进行双站联合观测下的目标姿态并行融合估计,同时与各单站观测下的姿态结果进行比较。图6给出了四种双站观测方案下姿态角分量估计误差曲线,由图中看出,双站观测总体上具有比各自单站观测更小的姿态估计误差。
从各双站观测方案横向比较来看,图6(d)的双站观测方案明显比图6(a)和6(b)两者的双站观测方案的姿态估计误差更小。为进一步量化分析估计误差和站点间距的关系,在表1列出了双站观测方案下姿态估计器收敛后各姿态分量误差,从表1可以看出,站1和站3联合观测下的滚转角估计误差比站1和站4小,站1和站3联合观测下的俯仰角估计误差与站1和站4相等,在其他情况下单项姿态角估计误差均随站点间距离增大而相应减小。
为表示站点间距对姿态估计误差的影响,根据式(25)计算姿态RMSE,见表1最后一行,可以看出,随着站点沿纬线方向与站1之间距离的增大,姿态角估计误差相应减小,这也表现出姿态RMSE指标的合理性。
与姿态角的估计相一致,根据状态向量,算法也得到了目标角速度估计的结果,站点之间角速度估计结果与姿态角估计值相一致,由于本文着重体现姿态估计方案的优劣,并由于姿态角对角速度的积分关系,姿态角估计值对算法的优劣更为敏感,而角速度对算法差异的显示度不如姿态角显著,因此本文只给出姿态角估计结果的对比。
3.2.2沿经线方向设置站点
以站1为基准站点,分别与站6、7、8、9组合构成双站观测方案,并按照2.4节算法进行目标姿态

图6 沿纬线方向双站联合观测与单站观测下的姿态估计误差对比

表1 沿纬线方向双站联合观测下姿态估计器收敛后的误差Table 1 Convergence errors of the attitude estimator by two-sites joint observation along the latitude line
的并行融合估计,其仿真结果和图6相似,对于三个姿态角分量,双站观测总体上具有比单站观测方案更小的姿态估计误差。
在表2列出双站观测下姿态估计器收敛后的误差,从表中看出,站1和站8联合观测下的滚转角误差比站1和站9小,站1和站6联合观测下的俯仰角误差与站1和站7、站1和站8相等,其他情况下单项姿态角误差均随站点间距的增大而减小。
根据式(25)计算姿态RMSE,见表2最后一行,该值的变化反映出随着站点沿经线方向与站1之间距离的增大,姿态角估计的误差相应减小。
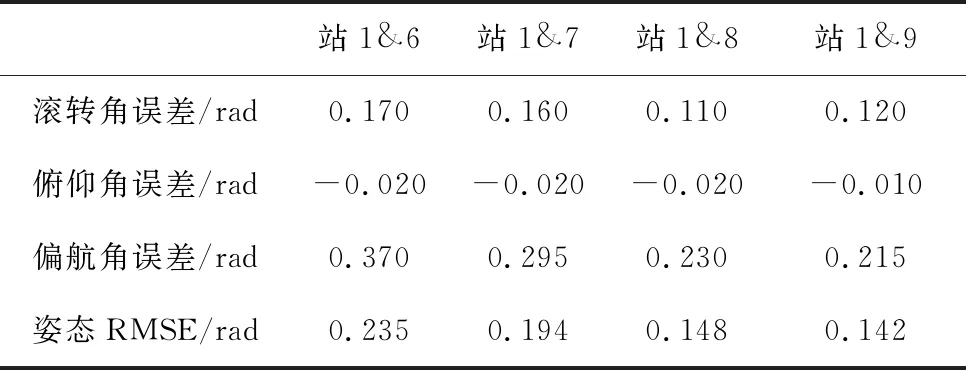
表2 沿经线方向双站联合观测下姿态估计器收敛后的误差Table 2 Convergence errors of the attitude estimator by two-sites joint observation along the longitude line
3.3 站点数量对姿态估计的影响
3.2小节表明在增加观测站间距离的情况下基于双站观测的姿态估计性能可进一步提升,但即使是站1和站5、站1和站9这两种组合,虽然站点间距离相当远,仍然存在较为明显的姿态估计误差。为此,考虑进一步增加站点数量,进行三站联合观测,验证站点数量对于姿态估计性能的影响。
选取站5、站9和站1构成三站观测方案,其姿态估计的结果如图7所示。从图中看出,三站观测下各姿态角估计误差都收敛很小,且收敛速度在各方案中最快,其中双站观测虽在个别姿态角分量上误差较小,但三站观测表现出更好的综合性能。
本研究也尝试了其它的三站观测方案,它们一致表现出比双站观测更好的估计性能。从单站观测、双站观测以及三站观测的分析看出,随着站点数量增加姿态估计的误差逐步减小且收敛速度获得提升,这说明在弱特征目标姿态估计中,站点数量的增加是提升姿态估计性能的有效途径。

图7 三站联合观测与双站联合观测姿态估计误差对比
3.4 站点方位对姿态估计的影响
为了分析联合观测时所选取的站点相对于卫星的方位对姿态估计的影响,我们提出以靠近星下点轨迹的站1为中心,在对太阳光线反射的相反方向上等距选取站点的方案。
根据3.2节站1和站5在卫星对太阳光线反射的相同方向上,在站5相对于太阳光线反射的相反方向上,沿纬线等距选取站10与站1进行联合观测,所得到的姿态估计结果如图8所示。从图中可以看出,站1和站10联合观测的姿态估计误差相比于站1和站5小很多,既消除了原方案明显的误差,而且算法收敛速度很快。
同样地,站1和站8在卫星对太阳光线反射的相同方向上,沿经线等距反向选取站11与站1进行联合观测,姿态估计结果表明,新方案的姿态估计误差相比于站1和站8小很多,其收敛速度与估计误差与图8中站1和站10所构成方案的表现相似。
为进一步验证该规律,相对于站1,在倾斜方向上等距地增加站12和站13,其中站12和站1在卫星对太阳光线反射的相同方向,站13和站1在卫星对太阳光线反射的相反方向。这两个站点分别与站1进行联合观测,得到的姿态估计的收敛速度、估计误差也与图8相似,站13和站1联合观测的姿态估计结果相比于站12和站1的结果提升显著。上述三组对比实验表明,沿卫星对太阳光线反射的相反方向设置不同站点较在相同方向设置不同站点所获取的信息的互补性更强,该互补性的增强导致算法对卫星姿态估计性能有明显提升。

图8 站1分别与站5、站10组成双站联合观测方案时的姿态估计误差对比
4 结 论
本文研究光度曲线波动不明显的弱特征空间目标姿态估计问题,分析了此类目标在不同站点间所获取光度曲线具有差异的特征进而提出了以空间换取精度的设想,并为弱特征目标的姿态估计设计了基于多站联合观测的并行融合解决方案。通过沿经线方向、纬线方向布置站点,发现随着站点间距离的增大姿态角估计的均方根误差相应减小;该研究同时表明双站观测方案相比于单站观测方案具有更小的姿态估计误差,在此基础上设计了三站联合观测方案,表明三站观测相比于双站观测具有更小的姿态角估计误差以及更快的收敛速度。考虑到站点方位对多站观测方案性能的影响,我们发现通过沿空间目标对太阳光线反射的相对方向布置站点可使姿态角估计误差显著减小,且收敛速度显著提升。本文通过对站点间距离、站点数量以及站点方位三方面因素的研究,揭示了在多站观测下可为空间弱特征目标姿态估计提供可行的途径,且有规律可以遵循。通过本文的研究为弱特征目标的研究提供了解决方案。

