基于多位置NWP 和门控循环单元的风电功率超短期预测

杨 茂，白玉莹

（现代电力系统仿真控制与绿色电能新技术教育部重点实验室（东北电力大学）,吉林省吉林市132012）

0 引言

风电功率预测及其在调度运行中的应用是促进新能源消纳的基础,研究风电功率预测技术有助于削弱风电功率并网时对电力系统带来的不利影响,降低电网的运行成本,提高系统运行的可靠性,有效保证电网安全［1］。

目前,神经网络技术已成功应用于风电功率预测领域,通过挖掘输入与输出之间的隐含关系,解决静态模型问题进而实现风电功率预测［2］。但是风电功率属于非平稳时间序列,其变化规律不仅与当前状态有关,还受历史数据变化过程的影响。随着大数据的发展,深度学习近年来引起国内外研究学者的广泛关注,循环神经网络（recurrent neural network,RNN）应运而生,其中最有代表性的长短期记忆（long short-term memory,LSTM）网络是一种时间循环网络［3］。目前已有研究［4］证明LSTM 网络可有效提高风电功率超短期预测精度,但模型运行时间较长,不适用于工程实际,因此有研究学者在LSTM 网络的基础上提出了门控循环单元（gated recurrent unit,GRU）,在确保精度的同时,使模型结构更简单,计算时间更短。

文献［5］提出一种结合卷积神经网络（convolutional neural network,CNN）和GRU 的风电功率超短期预测模型,引入CNN 对GRU 模型中的隐藏状态进行压缩,缩短计算时间的同时也克服了训练过程中容易出现的梯度消失和梯度爆炸问题,但对于数值天气预报（NWP）的特征没有进行筛选,易出现输入信息冗余。文献［6］考虑多位置NWP 和非典型特征,利用最大相关-最小冗余原则提取输入变量,说明多位置NWP 和非典型特征均包含有效信息,但预测模型为浅层神经网络,结果存在不确定性。文献［7］提出一种基于提升回归树和随机森林（random forest,RF）的风电功率预测方法,可以有效地提取数据中包含的信息,明显改善预测精度。

本文为充分利用NWP 中的有效信息,考虑多个风电场的空间相关特性,提出一种基于多位置NWP 和GRU 的风电功率超短期预测模型。首先,通过RF 分析多位置NWP 信息对于风电场发电功率的重要度,基于累积贡献率提取NWP 特征,按照重要度和关联度大小分配权重,将加权的特征作为预测模型的输入,并与灰色关联提取的方法进行对比分析。然后,选取改进的灰狼寻优算法对GRU 模型进行参数优化,建立多变量时间序列预测模型。最后,算例采用中国某风电场的实测数据进行验证,结果表明,本文方法可有效提取NWP 特征中包含的信息,提高预测精度和训练速度。

1 基于RF 的多位置NWP 特征提取

1.1 多位置NWP

风电功率预测模型主要建立NWP 信息与风电功率之间的对应关系,输入变量以NWP 信息为主［8］。不计机组损耗,风电功率可表示为:

式中:P 为风电机组输出功率；Cp为风能利用系数；ρ为空气密度,受温度、湿度、气压等因素影响；A 为风电机组叶轮扫风面积,与风向等因素相关；V 为轮毂高度处风速。

NWP 数据由第三方预报平台购买的气象产品提供,包含多个区域不同高度的风速和风向等气象信息,然而过多的NWP 信息加入预测模型会增加模型的冗余度和训练难度。因此,在进行预测之前需要筛选NWP 信息,提取出对风电功率超短期预测影响较大的特征作为模型的输入,从而提升模型预测精度［9］。

在风能资源十分丰富的地区,用于风电场发电的风系,其空间尺度通常为数百米以上［10］,考虑空间相关性进行风电功率超短期预测的基本思想为:邻近地区不同风电场的风速和风向等气象信息具有一定的相关性［11］,利用风电场群中其他风电场的NWP 信息来提高本地风电场功率的预测效果。以往文献［12］只考虑单一风电场内的NWP 信息,忽略了邻近场站NWP 包含的有用信息,因此建模时应综合考虑多位置NWP 信息。

1.2 RF

常用的特征提取方法,如粗糙集、互信息和Pearson 系数,大都通过分析特征与功率之间的一致性、信息熵、相关系数等特性进行筛选,对数据质量要求较高［13］。RF 是对样本进行分类和预测的一种分类器,通过分析输入变量对分类或者预测结果的影响程度完成特征的提取［14］。本文将这一思想应用于风电领域,基于RF 计算NWP 特征对于功率数据的重要程度,提取风电功率预测模型的输入变量。

RF 通过随机有放回抽样（bootstrap sample）构建每个树的训练集,即每个树的训练集是样本集的非空真子集,假设某颗树m,存在部分样本没有参与该树训练集的生成,这些样本称为该树的袋外（outof-bag）样本。

模型基于袋外错误率（out-of-bag error）训练的计算方法如下:选出某个特征v 及RF 中的某颗树m；将该特征样本随机赋值,其余特征样本保持不变,放入所选树m 上,产生一个分类结果,计算误分率Om(v),即预测错误个数merr(v)与总数mall(v)的比例,作为RF 的袋外错误率,计算公式如式（2）所示。袋外错误率等同于RF 测试集的错误率,模型在测试集上表现好,说明泛化能力强,反之则说明泛化能力弱。

为考量NWP 特征对于功率数据的重要性,对NWP 中各个特征随机初始化,若其中某个特征对于功率数据较为重要,那随机赋值该特征后模型误差将会增大,平均精度下降值（mean decrease in accuracy,MDA）也会增大［15］,计算公式如下。

式中:M(v)为随机赋值某特征v 后的MDA；n 为RF中决策树的数目；O′m(v)为原始特征样本集的平均袋外错误率。M(v)下降越多,表示特征v 对于功率数据越重要。

1.3 基于累积贡献率的特征提取

累积贡献率［16］反映了NWP 特征对功率数据的影响程度。对于某风电场,通过RF 对该风电场的NWP 信息进行提取。为使模型泛化误差最小,需设置决策树的数目和每个节点的候选特征个数,然后按MDA 降序排列,计算NWP 中各个特征的累积贡献率βp,即

式中:N 为NWP 特征总数；p 为累积特征数。

2 风电功率预测模型

2.1 GRU

GRU 是LSTM 网络的一个简化变体,属于门控循环神经网络家族。GRU 中的更新门是由LSTM 网络中的遗忘门和输入门合并而成,模型架构更为简单,在保证模型预测精度的同时减少了计算量和训练时间［17］。

每个GRU 包括一个更新门u(t)和一个重置门r(t),在t 时 刻,GRU 接 收 当 前 状 态x(t)、上 一 时 刻的隐藏状态h(t-1),更新门同时进行遗忘和记忆2 个步骤,运算决定选择多少信息输入网络,遗忘多少过去的信息；重置门决定忘记过去的信息量；GRU 网络的输出h(t)最终由更新门和重置门的动态控制形成。GRU 内部结构如图1 所示,各变量之间的计算公式如下。

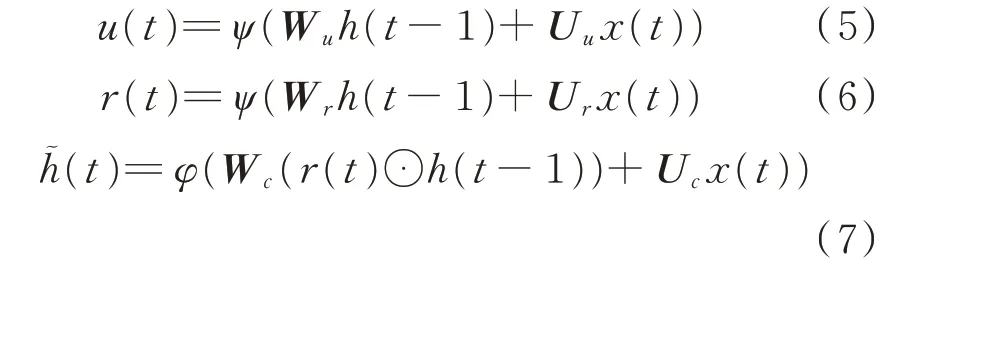
式中:Wu,Wr,Wc为连接隐藏层输出信号的参数矩阵；Uu,Ur,Uc为连接输入信号的参数矩阵；ψ(⋅)为激活函数,通常是sigmoid 激活函数；φ(⋅)为任何非线性函数（原型中是双曲正切函数）；h˜(t)为混合了细胞状态和隐藏状态的中间记忆状态；⊙为逻辑运算符,表示矩阵中对应的元素相乘。

图1 GRU 内部结构图Fig.1 Internal structure of GRU

2.2 改进GRU 参数寻优模型

灰狼寻优（gray wolf optimizer,GWO）算法［18］被广泛应用于参数寻优领域,具有收敛速度快、精确度高等优点。GWO 算法将寻优过程模拟为灰狼捕食猎物过程,算法核心内容参见文献［19］。

GWO 算法有较强的全局寻优能力,但是受参数初始化影响,前期的寻优能力较弱,可能无法搜索到最优解。基于此,本文对GWO 算法存在的缺点进行改进,利用φp准则优化的拉丁超立方抽样（LHS）策略［20］对GWO 算法的种群参数进行初始化,形成改进的GWO（IGWO）算法,一方面保证了种群初始参数抽样过程的稳定性,另一方面使得初始参数更均匀地分布在解空间中,有效提高GWO的收敛速度。

在对GRU 模型训练时发现,影响风电功率超短期预测精度的主要模型参数分别是权重学习速率和隐层节点个数。因此,本文采用IGWO 算法来寻找GRU 模型的最优参数组合,构建IGWO-GRU 模型的具体流程如图2 所示。

3 预测模型建立及评价指标

3.1 预测模型建立过程

本文预测单个风电场的发电功率,首先对风电场可用数据进行预处理,考虑多位置NWP 信息,通过RF 筛选并提取预测模型输入变量,建立基于IGWO-GRU 模型的风电场发电功率超短期预测模型,具体架构见图3。

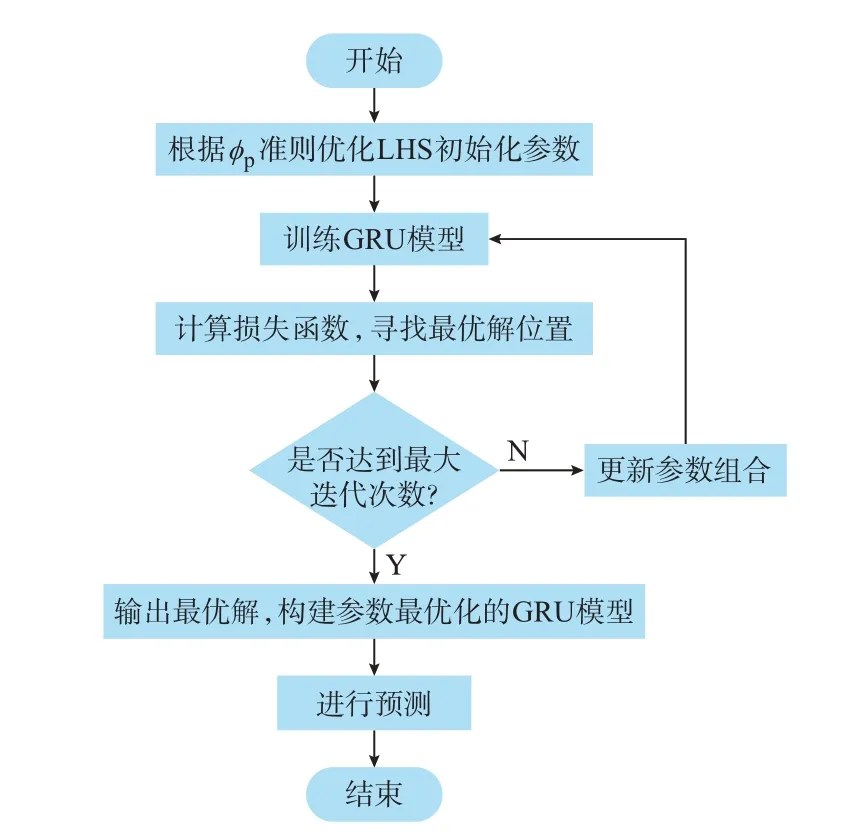
图2 IGWO-GRU 模型建立流程图Fig.2 Flow chart of establishment for IGWO-GRU model

图3 风电功率预测架构Fig.3 Architecture of wind power prediction

3.2 预测效果评估

以往相关文献［21］评价超短期功率预测结果选的是4 h 的平均值,但在《风电功率预测功能规范》［22］中对单个风电场超短期预测的考核已修改为第4 个小时。所以本文以归一化均方根误差（root mean square error,RMSE）为依据对风电场超短期预测第4 个小时的预测结果进行评价,利用最大绝对误差（maximum absolute error,MAE）分析超短期预测时偏差最大的情况,计算公式如下。

绝对误差E 为:

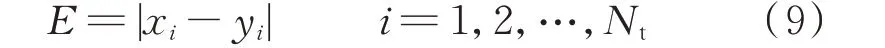
式中:xi为模型第i 步的预测值；yi为模型第i 步的实际功率值；Nt为预测步长,在本文中Nt取16。

归一化均方根误差Enrmse为:

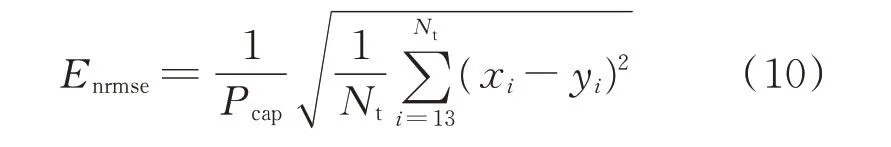
式中:Pcap为风电场额定装机容量。

归一化最大绝对误差Emae为:

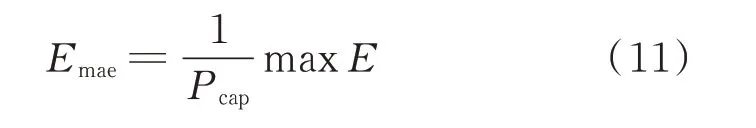
4 算例分析

4.1 数据说明

本文选择中国某地区的风电场群进行算例分析,该场群共有10 个风电场,每个风电场的可用数据为历史实测功率数据、测风塔数据以及配套的NWP 数据,风电场的分布见附录A 图A1。每个位置的NWP 数据包括24 项特征,具体特征名称及其含义见表A1。

在实际的风电场运营中,几乎每个风电场都会出现数据异常［23］,所以本文在预测前对数据进行处理:删除弃风数据,补齐时若缺失3 个点或3 个点以内,选用持续法补齐；若缺失超出3 个点,选用三次样条插值补齐；以装机容量替代大于装机容量的功率数据；以零替代小于零的功率数据。因NWP 不同特征之间量纲各不相同,为保证平等地考虑每一个变量与功率之间的关联程度,需对NWP 数据和功率进行最大最小归一化,将数据归一化到区间[0,1]内,即

式中:x 和x′分别为数据归一化前、后的值；xmax和xmin分别为样本数据中的最大值和最小值。

将归一化后的数据输入预测模型中,得到的功率数据需要经过反归一化,使其具有明确的物理含义,即

为了进一步反映不同输入变量对风电功率的影响程度,利用RF 量化分析NWP 特征对风电功率的重要度,模型输入变量的权重按照重要度大小分配,权重ω′v的计算公式如下。

式中:pv为经累积贡献率筛选后的NWP 特征总数；ωv为特征v 的重要度。

4.2 输入特征提取

以5 号风电场为例,首先通过RF 对5 号风电场对应的NWP 信息进行筛选和提取。由于RF 训练集采用的是有放回抽样,经多次试验发现采用70%的数据作为训练集时模型效果最优。当使模型泛化误差达到最小时,参数设置为决策树的数目n=1 000 和每个节点候选特征个数s=4。按MDA 降序排列计算各特征的累积贡献率。考虑多位置NWP特征时,每个位置的NWP 有24 项特征,共10 个位置,类似于单位置5 号风电场NWP 信息的建模过程。选择当NWP 特征的βp大于80%时的前p 个特征作为预测模型的输入变量。

为保证NWP 信息与风电功率相关性高的同时,缩减输入特征数目,结合累积贡献率选择前8 个特征加权后作为单位置NWP 预测模型的输入变量,建立RF-IGWO-GRU 模型,前12 个特征加权后作为多位置NWP 预测模型的输入变量,建立mRFIGWO-GRU 模型,即本文方法。

在利用灰色关联分析（gray relation analysis,GRA）方法［24］提取输入变量时,计算NWP 各特征与风电功率的灰色关联度及其累积贡献率。选择前6 个单位置NWP 特征加权值和前10 个多位置NWP特征加权值,分别建立基于单位置NWP 的GRAIGWO-GRU 模型和基于多位置NWP 的mGRAIGWO-GRU 模型。模型具体输入设置见附录A 表A2 和表A3。

4.3 模型对比分析

本文对5 号风电场进行功率超短期预测,该风电场的装机容量为45 MW,是该风电场群中装机容量最小的一个风电场,与2 号、3 号和8 号风电场距离较近,可用数据为2012 年全年实测风速、风向、发电功率以及配套的NWP 数据,时间分辨率统一为15 min。模型测试集的输入为预测时段加权后的NWP 信息和上一时段历史实测功率数据的归一化值,输出为预测时段反归一化后的预测功率值。

本文利用Python 平台中的Keras 框架构建基于GRU 模型的风电功率超短期预测模型。预测模型初始化参数为:模型网络隐藏层节点个数和权重学习速率由IGWO 算法确定,模型迭代次数为150,批处理量为1,采用sigmoid 函数作为GRU 模型的激活函数。

将5 号风电场每个季节前2 个月的数据作为模型的训练集,第3 个月的数据作为测试集,建立基于IGWO-GRU 模型的预测模型,进行一天滚动96 次,一次提前16 步的多步预测。正文中仅展示5 号风电场春季预测效果,夏季、秋季以及冬季的预测误差和训练时间见附录A 表A4。

5 号风电场功率的实际值与不同预测模型的第13 个预测值的对比效果见图4。24 h 内各模型的超短期预测第4 个小时指标的平均值见表1。由图4和表1 可知,本文方法的第13 个功率预测值与实际值吻合较好,在风电功率拐点处能跟随其波动趋势。mGRA-IGWO-GRU 模型虽然也可以跟踪功率变化趋势,但效果不及本文方法；而RF-IGWOGRU 模型和GRA-IGWO-GRU 模型的预测值则较为平缓,不能很好地跟随功率数据波动,说明仅选用单位置NWP 作为预测模型输入时无法有效利用与功率数据强相关的信息,而考虑多位置NWP 可充分利用其中的有效信息,改善模型预测效果。

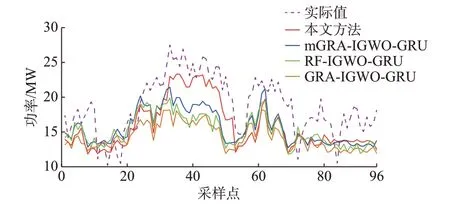
图4 5 号风电场功率实际值与各模型预测值Fig.4 Actual power value of No.5 wind farm and predicted values of various models

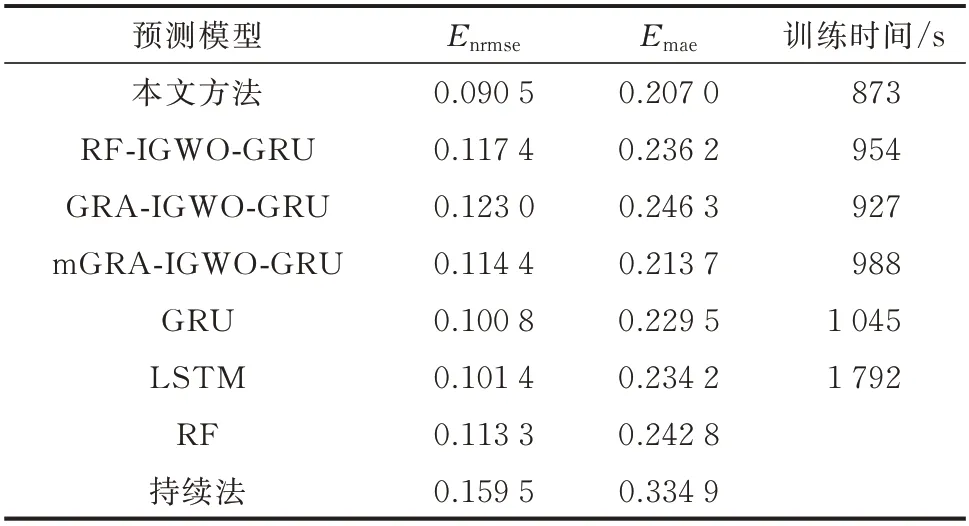
表1 5 号风电场各预测模型的预测误差和训练时间Table 1 Prediction error and training time of each prediction model for No.5 wind farm

为了更准确和清晰地体现出本文所提方法相较于其他常用预测方法的优势,图5 给出了5 号风电场各个预测模型绝对误差的频率分布,用于直观评判各模型的预测效果,其中GRU 和LSTM 模型的输入特征与本文方法一致,RF 模型输入为历史功率数据。

图5 5 号风电场绝对误差统计图Fig.5 Statistical diagram of absolute error for No.5 wind farm

结合图5 和表1 的结果可以看出,经IGWO 算法优化后的GRU 模型预测效果明显优于普通GRU模型,说明IGWO 算法可以更精确地找到模型最优参数组合,进而改善预测效果。与其他预测方法相比,本文方法的绝对误差峰值的出现位置较为靠前,最大绝对误差和均方根误差均小于其他方法；GRU模型与LSTM 模型相比,预测效果相当,但GRU 模型更简单,运行时间更短,为实现较高精度的在线超短期功率预测技术提供了可能。

选择9 号风电场进一步验证本文方法的有效性,该风电场的装机容量为400.5 MW,是风电场群中装机容量最大的一个风电场,与3 号和7 号风电场距离较近,可用数据与5 号风电场一致。GRU 模型参数中迭代次数改为200。9 号风电场功率实际值与不同预测模型的第13 个预测值对比效果如附录A 图A2 所示,各预测方法绝对误差统计图如图A3所示,春季、夏季、秋季以及冬季24 h 内的超短期预测的第4 个小时预测误差和模型训练时间如表A5所示。观察各模型预测效果与5 号风电场基本一致,进一步说明了本文方法可以有效提高预测模型精度。

5 结语

为充分利用NWP 信息,进一步提高风电场发电功率超短期预测的准确性,本文提出了一种基于多位置NWP 和IGWO-GRU 模型的风电功率超短期预测方法,通过算例分析,得到如下结论。

1）对GWO 算法进行改进,利用IGWO 算法来优化GRU 模型参数,可以有效改善预测效果。

2）风电场周围多个位置的NWP 数据包含更多的信息,考虑多位置NWP 的预测模型比只考虑单位置NWP 的预测模型精度更高。

3）在单/多位置NWP 情况下,利用RF 提取的输入变量对风电功率进行预测,与通过GRA 方法建立的模型相比,可更有效地利用NWP 信息,提高预测精度。

4）在风电功率预测领域,GRU 模型相较于LSTM 模型预测性能相当,但结构更简单,计算速度更快。

本文考虑多位置NWP 信息,进行单场风电功率的超短期预测,如何利用单场功率信息和NWP信息进而预测集群风电功率将是下一步的研究重点。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。