面向新能源消纳能力评估的年负荷序列建模及场景生成方法
曲 凯,李 湃,黄越辉,司刚全
(1. 西安交通大学电气工程学院,陕西省西安市710049;2. 新能源与储能运行控制国家重点实验室(中国电力科学研究院有限公司),北京市100192)
0 引言
近年来,随着新能源装机容量的迅速增长,中国的新能源消纳问题变得日益突出,定量测算未来年度省级电网的新能源消纳能力,对制定电网中长期运行方式和合理规划新能源装机时序有着重要的现实意义[1-2]。时序生产模拟方法是新能源消纳能力评估的重要技术手段之一,其基本原理是通过随机模拟生成一系列新能源发电与负荷全年序列,通过逐时段电力平衡计算,模拟新能源和常规电源的发电运行情况[3-5]。时序生产模拟能够充分考虑电源的运行方式、负荷与新能源出力的随机波动特性,计算结果更加科学合理。年负荷序列是开展时序生产模拟计算的重要输入,直接影响着新能源消纳能力评估结果的准确性[6]。
在进行负荷序列生成时,需要提取历史负荷的随机波动性和时序变化特性。目前,针对负荷序列生成的研究主要集中于典型日负荷或月负荷[7-11],年负荷序列的时间跨度更长、生成难度大,研究相对较少。文献[12-13]为评估大规模风电场接入对电力系统调峰的影响,基于历史数据提取各月最大负荷及大、中、小典型日负荷序列,然后从3 种典型日负荷中随机抽样生成全年的每日负荷序列。文献[14]考虑负荷与电量的关联性,基于季度电量弹性系数建立负反馈模型,对历史负荷序列进行修正得到新的负荷序列。以上方法并未充分考虑负荷的随机波动性,导致所生成的负荷序列场景过于单一,难以满足不同场景下新能源消纳能力计算的需要。
日负荷序列是构建年负荷序列的基础。目前,通常采用工作日和休息日分类的方式进行日负荷序列的建模分析。随着分布式新能源和需求侧响应规模的不断增长[15-16],负荷在日内的随机波动性越来越大,工作日和休息日的负荷特性界限在逐渐打破,传统的典型日划分方法已难以满足负荷序列分析和建模的需要。日负荷的随机波动性可由日负荷率、峰谷差率等指标的概率分布进行表征。目前,不同日负荷特性指标的概率分布通常是独立建模的[17],由于忽略了不同指标之间的关联性,独立建模会造成一定的偏差。Copula 函数是构建具有相关性随机变量联合概率分布的常用工具,目前已广泛应用于风电和光伏的相关性建模[18-20],但在负荷特性概率分布建模方面的研究还未见报道。
针对上述问题,本文提出了一种基于聚类分析和马尔可夫链的年负荷序列建模和场景生成方法。首先,基于自组织映射(SOM)聚类方法将全年负荷划分为不同类型的典型日,采用马尔可夫链技术描述不同典型日之间的状态转移关系。其次,基于核密度估计和t-Copula 函数,建立各类典型日下的负荷特性指标的联合概率分布模型。然后,采用马尔可夫链蒙特卡洛(MCMC)技术随机抽样确定每日的典型日类型和负荷特性指标。最后,建立日负荷序列的二次优化模型,通过优化求解得到满足日负荷特性指标且与历史负荷时序变化特性相一致的每日负荷序列,直至得到全年的负荷序列场景。算例基于中国某省级电网全年每15 min 的负荷数据进行测试,结果表明所提方法生成的年负荷序列在概率分布特性、时序特性、全年及各月特性负荷指标等方面均与历史负荷非常接近。最后,基于生成的负荷数据,对该省级电网未来年度新能源消纳能力进行评估,进一步验证了所提方法的有效性和实用性。
1 负荷典型日的分类
本章通过聚类分析将全年负荷分为不同的典型日,然后针对各类典型日进行日负荷特性的分析和建模,为后续负荷序列场景的生成提供基础。本文主要基于中国某省级电网全年每15 min 的电力负荷数据进行分析验证,为降低负荷量级带来的影响,需要对全年负荷序列进行标准化与反标准化处理,全年的电力负荷曲线及标准化和反标准化方法如附录A 所示。采用日负荷率、日峰谷差率、日最大负荷指标进行负荷日特性的分析,各指标的含义及计算公式见附录A。
1.1 传统的典型日划分
首先采用传统的典型日划分方式进行负荷特性分析。基于标准化后的全年负荷序列,将其划分为工作日、周末日和法定节假日,分别得到相应的日负荷簇。本文中的法定节假日共计35 d,主要包括了国家法定节日及其相邻的周末日。通过适当增加法定节假日内的样本数量,可以避免样本过少引起的日负荷特性指标概率分布过拟合的现象。各类典型日负荷簇、日平均负荷、日负荷特性指标分布结果见附录B。可以发现,工作日和周末日的负荷及特性指标的相似度非常高,法定节假日的负荷水平相对较低,并且与工作日和周末日的负荷特性差别较大。这说明传统的负荷分类方式难以实现该省电力负荷的准确分类。
1.2 基于SOM 聚类的典型日划分
为克服传统分类方式的不足,本文采用SOM网络进行负荷序列的聚类划分。受经济增长的驱动,该省下半年负荷用电量较上半年有明显增长(增长率约6%)。因此,本文对上半年(1~6 月)和下半年(7~12 月)的负荷分别进行聚类。由于法定节假日数量相对较少,全年单独列为一类,SOM 聚类分析只针对法定节假日之外的工作日和周末日。
SOM 网络属于无监督学习聚类算法,不需要事先给定聚类数目,在多维数据聚类时具有更高的精确性,非常适用于对高维负荷数据进行分类。采用SOM 网络进行聚类分析主要包括初始化、训练计算过程和聚类结果分析3 个步骤。首先,根据文献[21]中的经验公式,将SOM 神经元节点数设置为8×8=64。然后,采用随机初始化神经元初始权重、学习率的方式,分别选取高斯函数、t-Location 函数和Logistic 函数作为邻域函数进行测试。经验证,在不同的参数给定策略下,上、下半年负荷序列的最佳聚类数都收敛为3 类,这说明采用SOM 网络进行负荷聚类分析具有较强的鲁棒性。详细的最佳聚类数结果分析见附录C。
通过聚类得到的上、下半年的典型日负荷簇曲线和日负荷特性指标散点图如图1 所示。图1(a)和(b)中,红色曲线为聚类中心曲线。可以发现,上、下半年的日负荷曲线被划分为高、中、低3 类(分别对应类别1,2,3),日负荷特性指标也得到了合理的划分,验证了SOM 网络聚类方法的有效性。
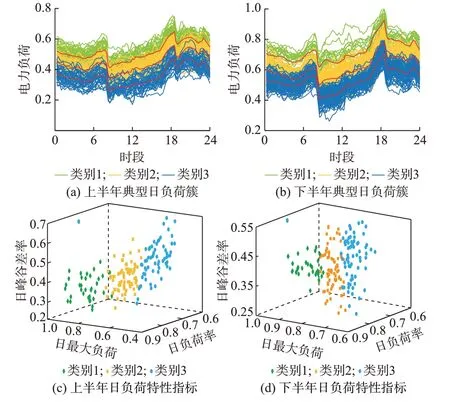
图1 上、下半年典型日负荷簇曲线和日负荷特性指标散点图Fig.1 Typical daily load cluster curves in the first and second half of a year and scatter diagram of characteristic indices for daily load
基于上、下半年的SOM 网络聚类结果,绘制全年每日类别色块图见附录D。由色块图结果可知,不同典型日之间的转换具有一定的随机性,并且在工作日和周末日之间的分布也没有明显的规律。这也进一步说明传统的工作日和周末日的划分方式难以实现全年负荷的合理分类。最后,采用马尔可夫链来描述不同典型日之间状态转移概率,并统计其累积转移概率矩阵,详情参见附录D。
2 日负荷特性指标联合概率分布建模
2.1 相关性分析
针对各类典型日,需要分别建立其日负荷特性指标的联合概率分布模型。由日负荷特性指标的定义可知,不同指标之间具有一定的关联性。不同日负荷特性指标之间的Pearson 相关系数如表1 所示。可以发现,日峰谷差率与日负荷率、日最大负荷之间具有较强的相关性。因此,在建立日负荷特性指标联合概率分布模型时,需要充分考虑它们之间的相关性。
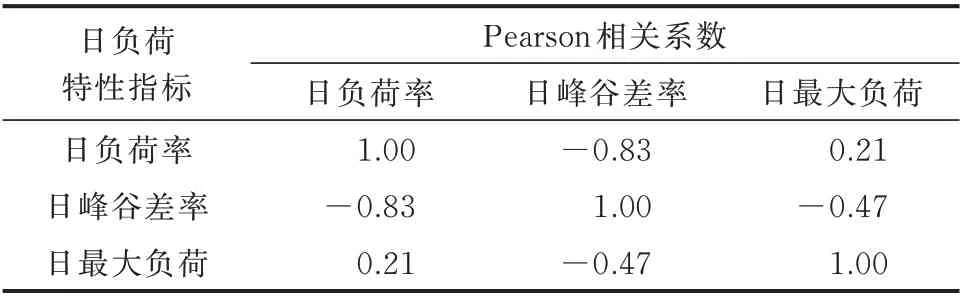
表1 日负荷特性指标之间的Pearson 相关系数Table 1 Pearson correlation coefficients between characteristic indices of daily load
2.2 Copula 联合分布模型
本节采用Copula 函数来描述日负荷特性指标的相关性结构,并构建其联合概率分布模型。Copula 函数可以精确描述多元随机变量之间的相关关系,其主要思想是将多元变量的联合分布函数拆分成多个边缘分布函数,再通过一个合适的Copula 函数将其连接。由Sklar 定理可知:若随机变量x1,x2,…,xn的 边 缘 累 积 分 布 函 数(CDF)为F1,F2,…,Fn,联合分布函数为G,则必存在一个Copula 函数C,有

因此,当日负荷特性指标的边缘概率分布和Copula 函数确定之后,即可得到其联合概率分布。
2.2.1 边缘概率分布拟合
已有文献中通常假定日负荷特性指标服从正态分布[20],然而,影响负荷波动的因素众多并且相互作用具有非线性,实际日负荷特性指标并不服从正态分布。本文采用非参数核密度估计法[22]来拟合各类典型日负荷特性指标的边缘概率分布,结果见附录E。可以发现,日负荷特性指标的概率分布具有明显的非对称性和非高斯性。将拟合得到的日负荷特性概率密度函数(PDF)进行数值积分,便可得到其边缘CDF。
2.2.2 Copula 函数建模
Copula 函数的选取对联合概率分布模型的准确性有着重要的影响,常用的Copula 函数包括正态Copula 函 数、t-Copula 函 数、阿 基 米 德Copula 函 数(Clayton 函数、Frank 函数和Gumbel 函数)等。首先,基于日负荷特性指标的历史数据,通过极大似然估计法来计算不同Copula 函数的最优参数[23]。然后,通过与经验Copula 函数之间的欧氏距离对比来确定最佳Copula 函数的类型,详细过程参见附录F。
不同Copula 函数的拟合偏差如表2 所示,可以发现各典型日类型中t-Copula 函数的拟合偏差均是最小的,因此本算例中的负荷数据适合采用t-Copula 函数进行建模。需要指出的是,最优的Copula 函数类型主要取决于数据自身的特性,如Gumbel-Copula 函数对曲线下尾部变化十分敏感,适合于风电相关性的建模[20]。
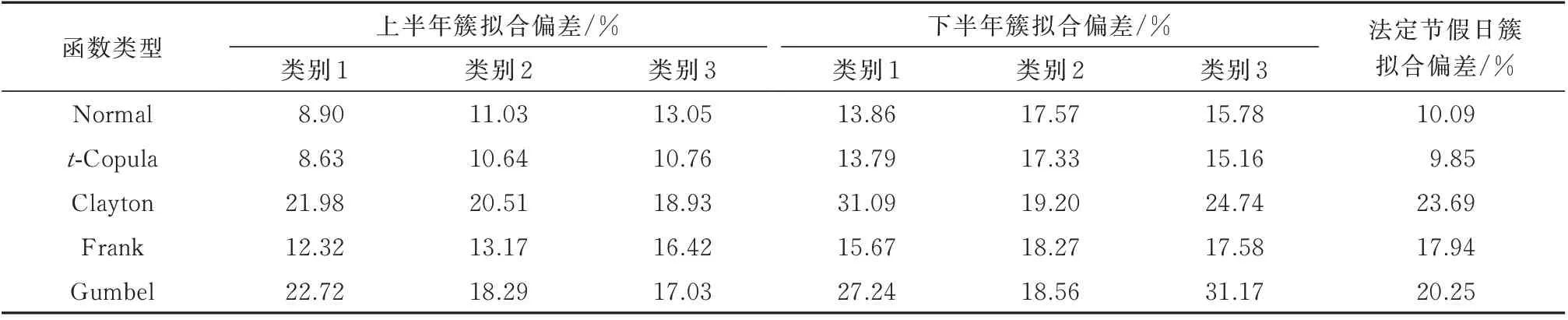
表2 日负荷特性指标联合概率分布模型拟合偏差Table 2 Fitting deviation of joint probability distribution model of characteristic indices for daily load
3 年负荷时间序列场景生成
3.1 负荷序列场景生成流程
采用MCMC 技术随机抽样生成年负荷序列场景,流程图参见附录G,具体步骤如下。
步骤1:对全年负荷序列进行标准化处理。
步骤2:对全年日负荷进行聚类分析,分别得到各类典型日负荷簇。
步骤3:计算累积转移概率矩阵及其日负荷特性指标。
步骤4:分别建立各类典型日负荷特性指标的联合概率分布模型。
步骤5:通过随机抽样确定全年第一日的典型日类型及初始时刻负荷值。
步骤6:基于当日的负荷特性指标联合概率分布,随机抽样生成日负荷特性指标。
步骤7:从该典型日对应的历史负荷序列簇中选择基准负荷序列。选择的标准是与所抽取的日负荷特性指标之间欧氏距离最小的历史日负荷。
步骤8:基于随机抽样的日负荷特性指标、初始时刻负荷和负荷基准序列,建立日负荷序列优化模型,求解该模型得到当日各时刻负荷值。
步骤9:基于典型日累积转移概率矩阵和当日的典型日类型,通过随机抽样确定下一日的典型日类型。
步骤10:基于相邻两日连接时刻的负荷波动量概率分布,通过抽样确定后一日初始时刻的负荷值。
步骤11:重复步骤6 至步骤10 直至得到全年标准化后的负荷序列。
步骤12:重复步骤5 至步骤11,直至得到所需数量的负荷序列场景。
步骤13:根据未来年度最大负荷与峰谷差率指标预测值,通过反标准化得到最终的全年负荷序列场景。
需要注意的是,在步骤9 中,上、下半年是分别基于各自典型日的状态转移矩阵来确定下一日的典型日类型。此外,以上流程中的典型日状态转移抽样主要针对法定节假日之外的日期,法定节假日的日期是直接固定的,其日负荷序列是通过日负荷特性指标的随机抽样和日负荷序列优化模型确定的。
3.2 日负荷特性指标随机抽样

3.3 日负荷序列优化模型
日负荷序列优化模型用于重构每日的负荷序列,使其同时满足日负荷特性指标与基准负荷的时序特性。
3.3.1 目标函数
模型优化目标为生成的日负荷序列与日负荷基准曲线之间的误差平方和最小,即
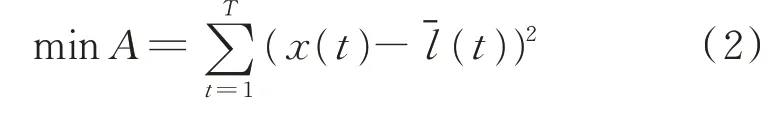
式中:A 为目标函数;x(t)为优化变量,表示t 时刻的负荷大小(t)为t 时刻的基准负荷值;T 为每日负荷样本点数。在该目标函数下,可以保证各时刻的重构负荷与基准负荷的变化趋势相近。
3.3.2 约束条件
1)日负荷率约束
日负荷率约束的数学形式如下。

式中:α 为日负荷率;γ 为日最大负荷。该约束表示当日的负荷率与随机生成的日负荷率指标相等。
2)日峰谷差率约束
日峰谷差率约束的数学形式如下。

式中:tmin为基准负荷曲线中最小负荷出现的时刻;β为日峰谷差率。该约束表示最小负荷出现的时间与基准负荷曲线相同,并且日峰谷差率与随机生成的日峰谷差率指标相同。
3)日最大负荷约束
日最大负荷约束的数学形式如下。
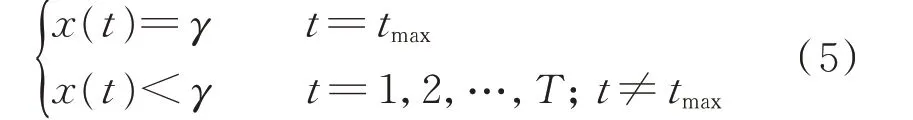
式中:tmax为基准负荷曲线中最大负荷出现的时刻。该约束表示最大负荷出现的时刻与基准负荷曲线最大负荷出现的时刻相同,并且日最大负荷与随机生成的日最大负荷指标相同。
4)日初始时刻负荷约束
日初始负荷约束的数学形式如下。
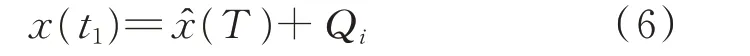
式中:t1为初始时刻;ˆ(⋅)为前一日负荷数据;Qi为从波动分量集合Q 中抽取的随机波动分量。
上述优化模型为二次规划模型,可调用Cplex等商业优化包进行求解。
3.4 日初始时刻负荷抽样
相邻日负荷序列在连接时刻的负荷波动具有一定的趋势性,在抽样生成每日初始时刻负荷时,需要考虑上一日最后时刻的影响。统计历史每日负荷序列连接时刻的波动分量,采用核密度估计方法得到波动分量的拟合分布,结果参见附录H。由附录H可知,相邻日连接时刻的负荷波动通常为负值,这是由于每日的最小负荷通常出现在次日凌晨,进入午夜后负荷通常呈下降趋势。基于波动分量的拟合分布,随机抽取波动分量并将其叠加至前一日最后时刻的负荷,进而得到后一日初始时刻的负荷,并将其作为3.3 节中日负荷序列优化模型的边界条件。通过该方式可以保证相邻日负荷连接时刻的变化趋势与历史负荷一致。
4 算例测试
基于附录A 中的负荷数据开展方法测试,并与文献[12]中的方法进行对比。该方法被用来分析大规模风电接入后电网的调峰能力,具有较好的计算效果。首先,分别采用2 种方法生成100 条年负荷时间序列场景,所生成的负荷序列场景与历史负荷的年最大负荷相同,并对生成负荷的特性、差异性和状态转移特性进行测试。然后,基于该电网未来年度的最大用电负荷预测生成100 条负荷序列场景,开展未来年度全省新能源消纳能力测算,验证所生成负荷的合理性。
4.1 负荷特性评价指标
1)PDF 和CDF
PDF 和CDF 能够反映年负荷序列的概率分布特性。
2)自相关函数和偏自相关函数
自相关函数(auto-correlation function,ACF)描述了在不同时滞范围之内负荷序列与自身数据之间的相关关系。偏自相关函数(partial auto-correlation function,PACF)描述了负荷序列与自身数据在不同时滞上的相关关系,消除了较短时滞内数据的间接影响。PACF 是对ACF 的一个补充,两者能够更全面地描述负荷波动的时序特性[25]。ACF 和PACF 的计算公式参见附录I。
3)全年及各月的负荷特性指标
全年及各月的负荷特性指标包括全年和各月的负荷率与平均峰谷差率,用于分析中长期负荷特性,其计算方法与日负荷特性指标类似。
此外,本文采用残差平方和(residual sum of square,RSS)[26]来定量比较上述指标的效果,计算公式参见附录I。
4.2 负荷场景评价
为直观比较,本算例中随机选取了一条生成负荷序列进行对比,并对负荷序列进行了归一化处理。图2(a)和(b)分别展示了所提方法和对比方法得到的年负荷时间序列的PDF 和CDF 结果。显然,所提方法结果与历史负荷更加接近,说明所提方法能够很好地描述历史负荷的概率分布特性。由于对比方法未考虑历史日负荷序列的多样性,因而难以反映出历史序列的概率分布特性。图2(c)和(d)分别为ACF 和PACF 结果对比,所提方法的ACF和PACF 结果与历史序列更加接近,说明所生成的负荷场景能够很好地反映出历史负荷序列的时变特性。
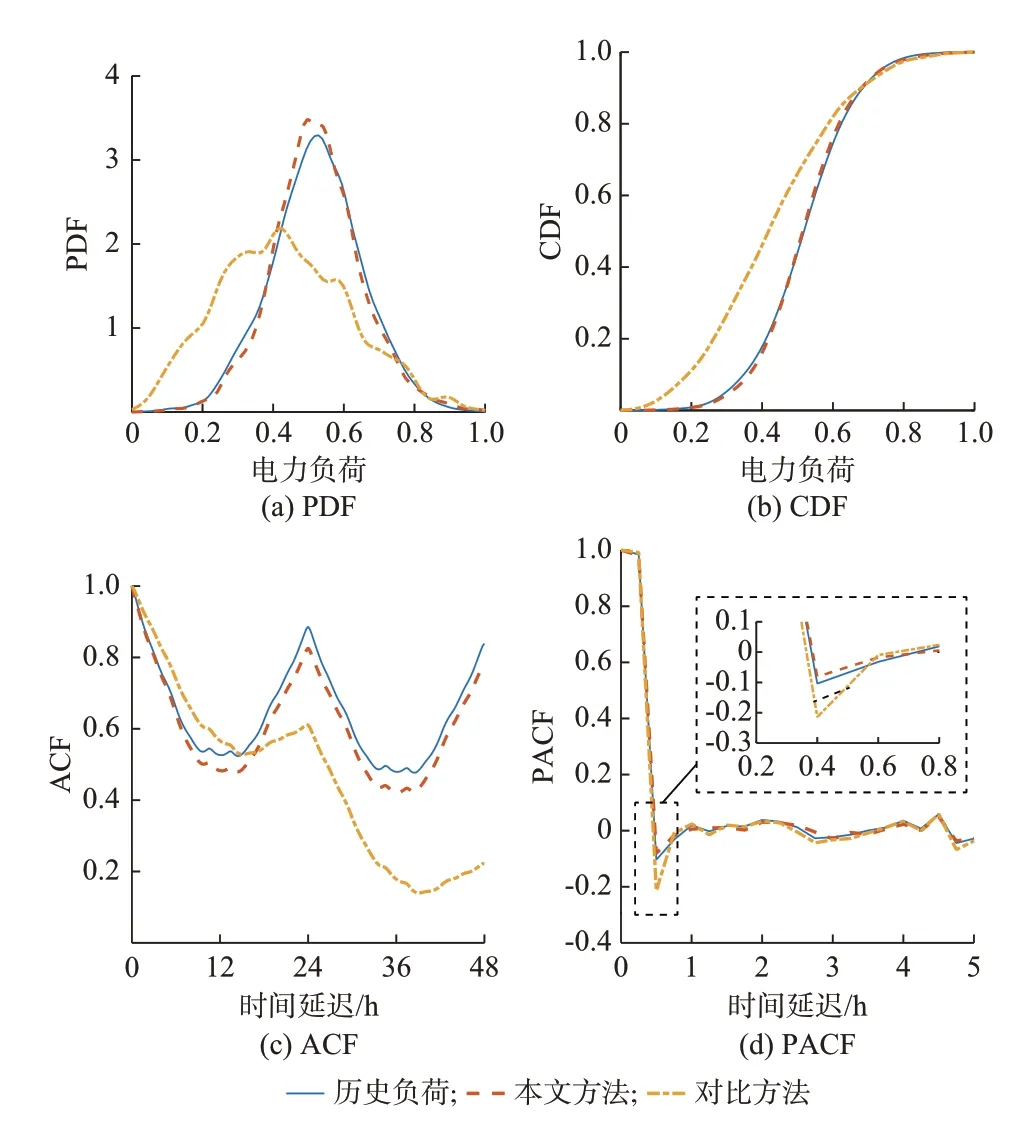
图2 年负荷时间序列评价指标结果对比Fig.2 Comparison of evaluation indices for annual load time series
PDF,CDF,ACF 和PACF 的RSS 结果如表3所示,显然所提方法的指标偏差均明显小于对比方法。表4 展示了2 种方法生成的负荷序列的全年和各月的负荷率与平均峰谷差指标结果,其中与历史负荷指标更接近的结果为红色数值。结果显示,在大部分情况下,所提方法生成的负荷序列指标与历史序列更加接近。

表3 年负荷特性指标的RSS 对比Table 3 RSS comparison of characteristic indices for annual load
4.3 负荷序列差异性与鲁棒性验证
为满足新能源电力系统时序生产模拟计算的需要,所生成的负荷需要具有一定的每日差异性和鲁棒性。本文采用全年负荷序列每日之间的欧氏距离来衡量每日负荷差异性。历史负荷与2 种方法生成的负荷序列的两日负荷之间欧氏距离的统计概率区间分布偏差结果如表5 所示。结果显示,所提方法生成的负荷序列的差异性与历史负荷序列的差异性更接近,说明本文方法能够很好地再现历史负荷序列的每日差异性。
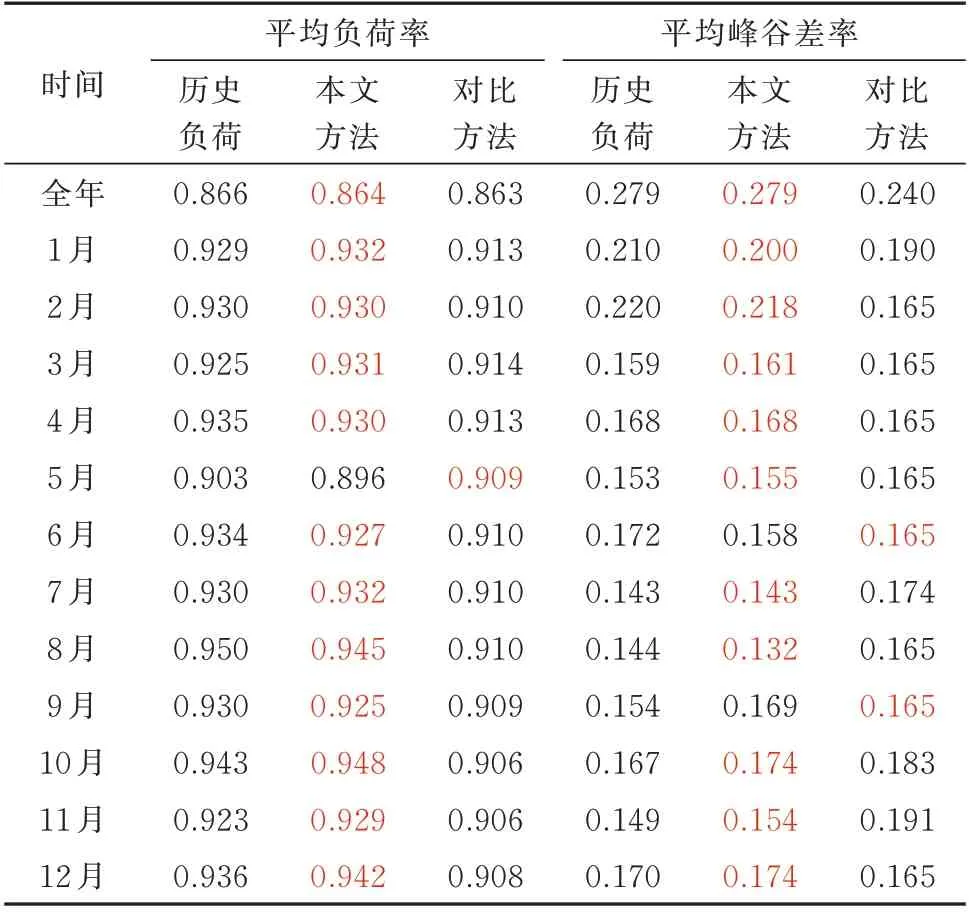
表4 全年和各月的平均负荷率和峰谷差指标对比Table 4 Indices comparison of annual and monthly average load rate and peak-valley difference
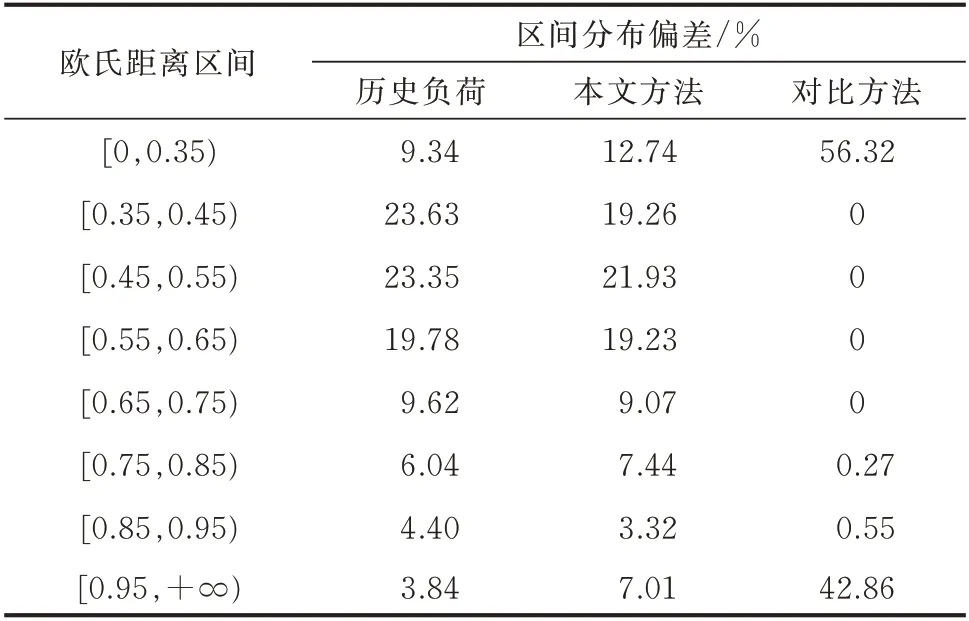
表5 序列差异性统计概率区间分布偏差对比Table 5 Comparison of interval distribution deviation of sequence difference statistical probability
为验证所生成负荷序列的鲁棒性,对所提方法生成的100 个负荷序列的年负荷率和平均峰谷差率的概率分布进行统计,结果如图3 所示。图3(a)和(b)中,红色虚线分别表示历史负荷的负荷率(0.866 5)和峰谷差率(0.279)。经统计,生成负荷序列的年负荷率和平均峰谷差率变化幅度在历史负荷指标的±0.5%和±3%内。这说明所生成负荷的特性指标波动性较低,验证了所提方法的鲁棒性。最后,所提方法生成的某7 日内20 条负荷序列场景和历史负荷序列如附录J 所示。可以发现所生成的负荷序列不仅具有明显的差异性,并且能够很好地反映历史负荷序列的时序性和变化趋势,验证了所提方法的有效性。
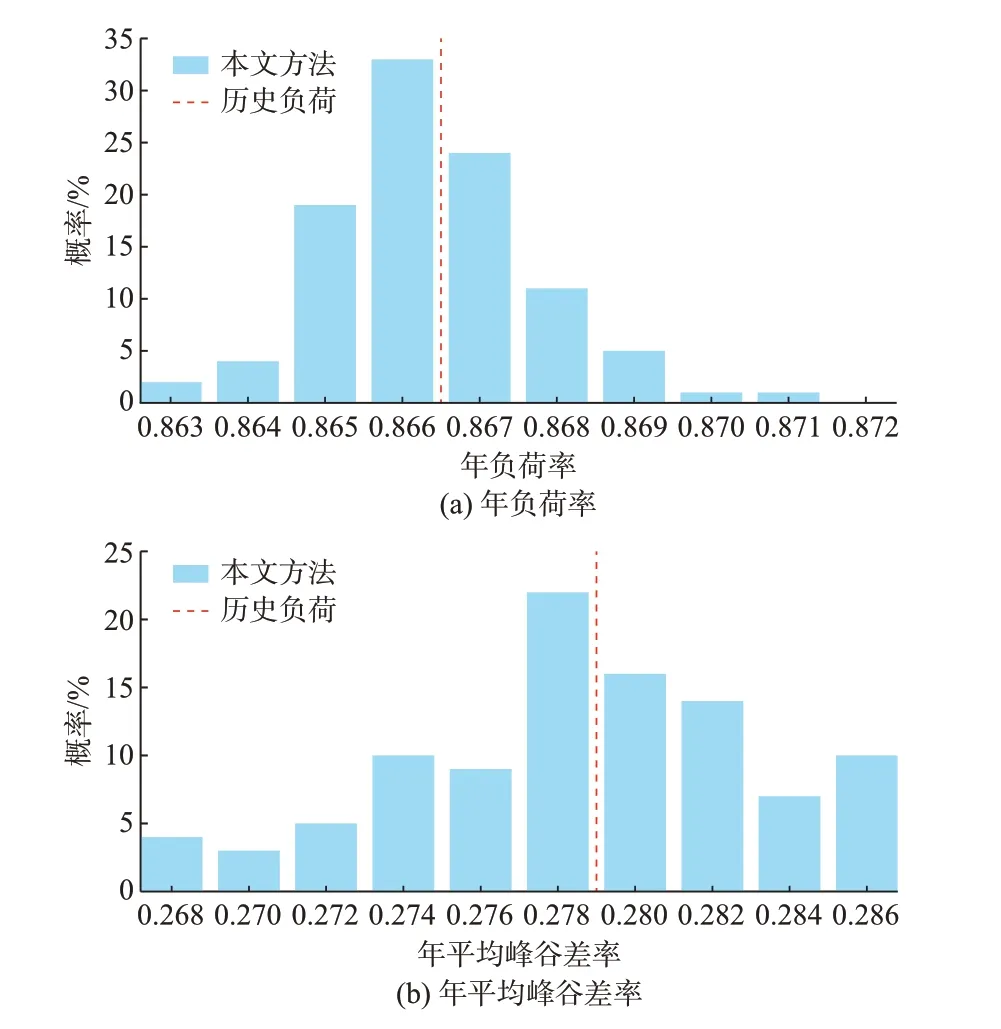
图3 100 条模拟负荷时间序列的年负荷特性指标分布Fig.3 Indices distribution of annual loads for 100 simulated load time series
4.4 典型日状态转移特性验证
在马尔可夫性假设下,当生成负荷数量足够多时,典型日的状态转移概率将服从稳定的极限分布。由于实际负荷的长度为一年,需要验证所生成负荷场景的典型日状态服从马尔可夫性。基于上、下半年状态转移矩阵,分别生成大量时长为1~60 个月的模拟负荷序列,并计算各状态转移矩阵与历史负荷状态转移矩阵的2-范数,结果如图4 所示。图中红色实线为所有结果的期望值,橙色散点为样本值。可以发现当负荷时长为半年时,其状态转移矩阵与历史负荷之间偏差的期望值就已经较小。这说明在生成大量年负荷场景的情况下,典型日的状态转移特性与历史负荷序列是非常接近的,即生成的负荷序列场景依旧存在马尔可夫性。

图4 状态转移概率矩阵偏差曲线Fig.4 Deviation curve of state transition probability matrix
4.5 省级电网新能源消纳能力测试
针对负荷所在的省级电网,采用文献[1]中的新能源时序生产模拟方法开展未来年度新能源消纳能力的测算。全网各类型电源装机容量及占比预测如附录K 所示。该省份新能源装机占比高达34.8%,属于典型的新能源电力系统[3]。不失一般性,按照5%的用电量增长作为未来年度基础负荷,并采用本文方法生成100 条负荷序列,所生成的负荷序列与基础负荷具有相同的年最大负荷值。针对所有的负荷序列,考虑新能源理论发电功率、火电机组在供热期与非供热期的运行方式、机组检修安排、省级联络线计划等,开展新能源消纳能力的测算。除负荷序列不同外,所有案例的其他边界条件均相同。
不同负荷序列得到的全省新能源消纳量结果如图5 所示。
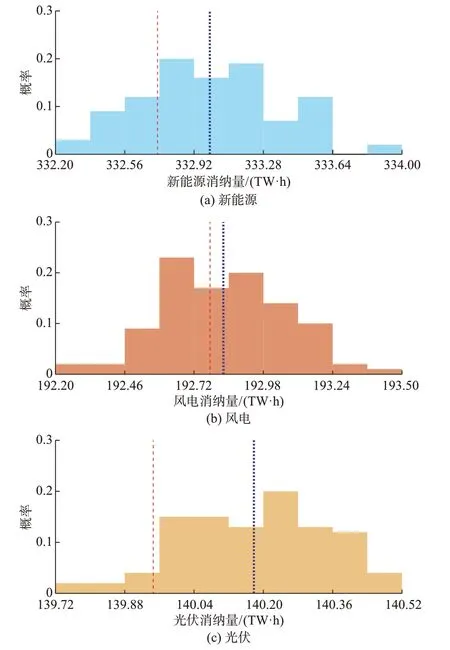
图5 新能源消纳量结果Fig.5 Consumption results of renewable energy
图5(a),(b),(c)中红色和蓝色虚线分别表示新能源、风电、光伏的基础负荷消纳量(332.7,192.8,139.95 TW ⋅h)和生成负荷消纳量期望(333.0,192.84,140.17 TW ⋅h),可以发现生成的100 条负荷序列对应的新能源总消纳量结果的波动量在0.18 TW ⋅h 以内,相对消纳量期望值的变化幅度不超过±0.6%,风电和光伏发电消纳量的偏差波动量分别不超过0.12 TW ⋅h 和0.08 TW ⋅h。生成负荷序列的新能源消纳量期望值与历史序列的消纳量之间的偏差不超过0.03 TW ⋅h,偏差幅度不超过0.1%。以上结果说明所提方法生成的负荷序列的新能源消纳量结果具有很好的收敛性和鲁棒性,能够满足新能源消纳能力计算的需要。
5 结语
本文提出了一种适用于新能源生产模拟计算的年负荷时间序列场景建模方法。首先,针对历史负荷序列的上半年、下半年和法定节假日分别进行SOM 聚类分析,实现了历史负荷序列合理的典型日分类,然后采用离散马尔可夫链刻画不同典型日之间的状态转移特性。其次,提出了基于核密度估计和t-Copula 函数的日负荷特性指标联合概率分布模型来准确刻画日负荷特性指标之间的相关性结构和联合概率分布特性;建立了日负荷时间序列优化模型,能够优化重构出满足给定日负荷特性指标与时序特性的日负荷序列。最后,提出了基于MCMC 技术的全年负荷序列场景生成方法,实现未来年度负荷序列场景的生成。
基于中国某省级电网全年负荷数据进行算例测试,测试结果表明:基于聚类分析的方法克服了传统的工作日和休息日分类不准确的问题,所生成的年负荷时间序列场景在概率分布特性、时序特性、全年及各月负荷指标、日负荷序列的差异性等方面均与历史负荷非常接近。算例中也对典型日状态的马尔可夫性进行了验证,结果表明MCMC 方法生成的全年负荷序列能够有效还原出历史负荷序列典型日的状态转换特性。最后,基于所生成的负荷序列,采用新能源时序生产模拟方法开展该省级电网未来年度新能源消纳能力的测算,验证了所提方法的有效性和实用性。在下一步工作中将继续对所提方法进行完善,并对不同新能源装机占比的电网进行测试,以提高方法的普适性和通用性。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

