基于深度强化学习的风电场储能系统预测决策一体化调度
于一潇,杨佳峻,杨 明,高 源
(1. 山东大学电网智能化调度与控制教育部重点实验室,山东省济南市250061;2. 国网陕西省电力公司电力科学研究院,陕西省西安市710054)
0 引言
随着各国电力市场改革的深入,风电场作为发电商在市场内追逐自身发电利润最大化成为必然趋势。对于风电而言,其输出具有不确定性[1],如何在风电的不确定性条件下从电力市场获取最大利润成为风力发电决策与控制的重要问题。
风力发电机与储能系统(energy storage system,ESS)合作组成风储混合系统是解决上述问题的有效途径[2-3]。当前已有诸多研究针对储能系统在风电不确定性条件下的控制问题取得了进展。文献[4]提出了抽水蓄能电站控制的机会约束优化模型,以缓解风电场与抽水蓄能电站集成功率的波动,该模型中,风电功率预测误差服从正态分布。文献[5]通过离散傅里叶变换和离散小波变换将风电预测误差分解为不同周期的信号,提高了储能系统和常规机组的经济效益。文献[6]认为风电的波动特征随输出功率的大小而显著变化,并提出一种通用的概率分布来描述风电不确定性。文献[7]将强化学习理论引入风储合作决策中,建立了基于Qlearning 算法的两阶段学习模型。所训练的控制器能一定程度上消纳风电的不确定性,具有启发意义。
针对在风电不确定性条件下风电场储能系统的优化控制,当前研究遵循预测、决策相分离的调度模式,需要描述风电功率的预测结果。然而,用确定形式[8]、区间形式[9]、概率形式[10]、概率区间形式[11]来表达预测结果,都难以把数据中蕴含的决策信息完整地表述并提供给决策者,会存在信息的损失,影响决策效果。尤其风电的不确定性规律需要人为刻画以匹配数学优化算法,然而描述结果与实际的风电不确定性规律存在差异,降低了优化结果在实际问题中的可行性[12]。其次,对不确定性的处理增加了决策阶段的困难(通常包含:有限的计算资源和存储空间、较长的计算时间成本),区间优化、鲁棒优化、随机优化、随机鲁棒优化的决策方法都难以动态、实时地得到有效的决策结果。
深度强化学习(deep reinforcement learning)集成了强化学习与深度学习。强化学习善于解决连续决策问题,能在动态、不确定环境中通过反复试错探索的方式实现既定的长期目标[13]。深度学习能从高维度、连续的状态空间中提取高阶数据特征,其对含不确定性的风电场状态空间的表达能力以及特征挖掘能力已经在风电预测领域中得到证明[14-16]。因此,深度强化学习能应对含不确定性的高维度状态空间并直接建立、优化从状态到动作指令的映射关系[17],这为风电场储能系统调度提供了新思路。
本文提出基于深度强化学习的风电场储能系统预测决策一体化调度方法,令包含高维度原始气象数据的风电场状态直接驱动储能系统的控制。端到端(end-to-end)的一体化调度模式能最大限度地避免风电场中有效决策依据(包括风电不确定性规律)的损失,提升调度结果的可参考性。其次,将深度强化学习Rainbow 算法用于储能系统的优化控制,建立的储能系统控制器具备动态统筹多时段系统收益的能力,能最大化风电场的长期收益。
1 研究思路
1.1 预测决策一体化调度
电力市场环境下,风电场以最大化从市场中获得的收益为目标安排储能系统的充放电功率[18]。
预测、决策相分离的储能系统调度模式如附录A 图A1 所示。在该模式中,风电场预测系统的输入通常包含t 时刻风力发电机的实时及历史输出功率和风电场实时、历史甚至预测的气象数据(风速、风向、温度、气压等),输出是下一调度时刻(t+1 时刻)风力发电机的功率预测值。在得到预测结果后,风电场的储能控制器以、储能系统荷电状态(state of charge,SOC)和前瞻售电价格作为决策依据,输出储能系统的动作指令PESS,t+1。
传统调度模式存在预测、决策2 个独立阶段,每个阶段是一个独立的任务。预测结果的质量将直接影响到决策过程,进而影响整体调度效果。
本文提出的预测决策一体化调度模式将2 个独立的阶段合二为一,形成端到端的调度模式,如图1所示。
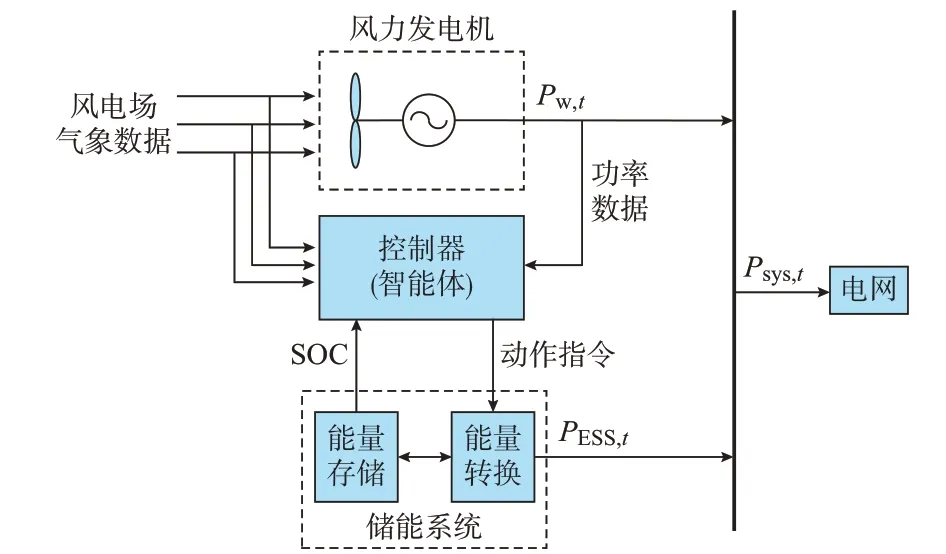
图1 预测决策一体化的储能系统调度模式Fig.1 Prediction and decision integrated scheduling mode for energy storage system
在预测决策一体化调度模式中,t 时刻的实时及历史风电功率以及风电场实时、历史、预测的气象数据和储能系统状态数据等都被作为决策依据输入到控制器中,控制器在大量的决策依据中自动提取有益于提高售电收益的数据特征,进而直接给出下一时刻储能系统的动作指令PESS,t+1。整个调度可描述为一个连续且动态的马尔可夫决策过程。
调度结束后,风电场在t+1 时刻向电网注入的功率Psys,t+1为:
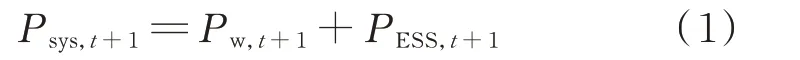
式中:Pw,t+1为t+1 时刻风力发电机的实际输出功率;PESS,t+1为正值表示储能系统处于放电状态,负值表示储能系统处于充电状态。
1.2 一体化调度模式下储能系统的优化控制
预测、决策分离时,预测阶段使用自身配备的预测算法,而优化算法的优化对象局限于决策阶段,2 个阶段同属一个调度流程却并无合作。其次,仅预测功率难以表征风电的不确定性。数学优化算法通常会额外要求将风电的不确定性描述成各类已知的概率分布。概率分布与实际风电不确定性规律的匹配程度影响优化算法的实际效果。预测、决策分离时储能系统优化控制的一般流程如附录A 图A2所示。
在预测决策一体化调度模式下,利用深度强化学习算法能端对端地优化整个调度流程。风电场的状态空间包含了风电不确定性等高阶数据特征,作为决策依据,避免了信息损失,具体如图2 所示。

图2 基于深度强化学习的储能系统优化控制Fig.2 Optimization control of energy storage system based on deep reinforcement learning
基于深度强化学习的储能系统优化控制由2 个环节组成:学习环节和应用环节。学习环节为基于历史数据与Rainbow 算法的离线训练过程,目的是不断更新控制器参数(即优化状态与动作指令之间的映射关系)。学习环节结束后,将收敛的控制器参数拷贝到应用环节,应用环节不再对控制器进行优化,而是让其专注于获取最高的调度收益。
将深度强化学习作为预测决策一体化调度模式下的随机优化算法,其优势如下。
1)深度强化学习能天然应对不确定性,且具备应对高维度状态空间的能力。
2)深度强化学习善于应对连续控制问题并注重当前决策对未来的影响。所建模型可以统筹多时段系统收益,最大化风电场的长期收益。
3)学习环节的训练时间不影响应用环节中控制器的决策过程,而应用环节就是实例的函数代入过程,决策时间几乎可以忽略。
2 深度强化学习Rainbow 算法
2.1 深度强化学习基本概念
强化学习的基本原理是不断鼓励智能体(控制器)以更高的概率输出可以带来高回报的可行动作。智能体本质上是一个从状态空间S 到动作空间A 的映射关系。通过对外部环境的试错探索(即提升外部环境返回的奖励rt),强化学习直接优化智能体内部的映射关系,无须考虑状态st与动作at之间的物理机理。强化学习基本流程如附录A 图A3所示。
在传统的强化学习算法中,映射关系通常用二维表格的形式表达,很难直接表征并处理连续的输入变量,必须对连续的状态空间进行离散、降维才能与算法匹配[19],造成不必要的信息损失。文中将深度强化学习Rainbow 算法应用到风电场的控制中,令控制器可以处理一体化调度模式下连续且高维度的风电场状态空间。
Rainbow 算法的基础框架是深度Q 网络(deeplearning Q network,DQN)[20]。因此,本章首先介绍DQN 算法,然后在其基础上阐述本文所用Rainbow算法的构架和优势。
2.2 DQN 算法
DQN 算法中,从状态空间到动作空间的映射关系被分为以下两部分:从输入状态到Q 值的映射关系与动作选择策略。Q 值的含义为:在经历无数次试验后动作所获得积累奖励的折扣期望值。动作选择策略根据Q 值确定最终的输出动作。已有研究表明,Q 值的引入让该类算法在处理存在不确定性的决策问题上具有优势[7]。DQN 使用深度神经网络来拟合从输入状态到Q 值的映射关系,使得控制器可以处理连续的状态空间。
拟合从输入状态到Q 值的映射关系的神经网络被称为评价网络(evaluation network)。DQN 的每一次学习过程可大致分为Q 值迭代和评价网络训练2 个过程。其中,Q 值迭代规则如下。

式中:Q(st,at;θt)为经评价网络得出的在状态st下动作at的Q 值;θt为评价网络的网络参数;θ-为目标网络(target network)的网络参数;α 为学习率;γ 为衰减系数。目标网络是评价网络在学习过程中的阶段性复制品,2 个神经网络共同完成Q 值的迭代,使迭代过程更加稳定,提升算法的收敛性。
在Q 值迭代完毕后,DQN 根据迭代前后Q 值的差来训练评价网络,该差值被称为时间差分偏差,表达式为:

式中:T 为时间差分偏差值。
评价网络训练过程中的损失函数L(θt)为:

神经网络的训练(即深度学习)要求输入样本之间相互独立,然而马尔可夫决策过程只能产生连续的过程化样本。为此,DQN 设置以回放缓存(replay buffer)为主的经验回放机制来打乱过程化样本。
2.3 Rainbow 算法
DQN 算法在收敛性、收敛速度和最终控制效果等方面仍然存在诸多不足。为提升该算法的性能,DQN 的各种改进算法被陆续提出。文献[21]提出的Rainbow 算法是一种以DQN 算法为框架、将各种改进算法融合的组合算法,其优势是使用者可针对不同的应用场景自主添加所需要的改进算法。
Rainbow 算法架构如附录A 图A4 所示,将优先回放缓存机制(prioritized replay buffer)[22]、双Q 学习(double Q-learning)[23]、竞 争 网 络(dueling network)[24]这3 类 改 进 算 法 和 辍 学 层(dropout layer)[25]技术集成到DQN 中,以提升控制器在本文应用背景下的表现。
1)优先回放缓存机制
DQN 算法中,回放缓存机制等概率随机地提取样本并用于评价网络的训练,未能衡量样本的质量,使得评价网络的训练效率较低。而优先回放缓存机制根据每个样本的时间差分偏差来确定其被采样的概率,如式(5)所示。

式中:Psam,t为样本被采样到的概率;ω 为用于调整时间差分偏差对采样概率的影响程度,即影响因子。
在优先回放缓存机制中,更频繁地提取时间差分偏差值较大的样本,显著加快了算法的收敛速度,减少评价网络收敛所需要的样本数量。
2)双Q 学习
在DQN 算法中,迭代后收敛的Q 值往往被高估。当过估计量非均匀时,收敛后的映射关系将不是最优状态。双Q 学习利用已有的2 个神经网络来改进Q 值的迭代规则,缓解了过估计现象。迭代过程中时间差分偏差的计算过程变更为:
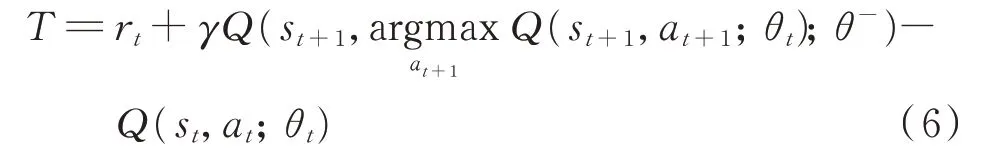
在本文背景下,双Q 学习的引入优化了动作空间中Q 值的分布,避免了次优控制策略的形成,进一步提升控制器为风电场带来的收益。
3)竞争网络
竞争网络对评价网络的输出层进行改进,使得Q 值能表示为更加细致的形式。改进后的评价网络有2 个输出分支,分别输出当前状态的价值v(st)和该状态下每个动作与状态相比的优势值A(st,at)。最终输出的Q 值计算式为:
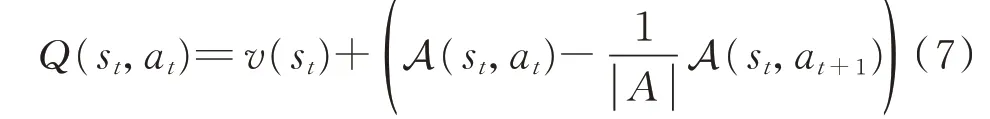
式中:|A|为动作空间中可行动作的个数。
从状态到动作的映射关系较为复杂,过多的可行动作和约束条件会减缓、阻碍映射关系的收敛。引入竞争网络能改善算法的收敛性并提升收敛速度。
4)辍学层
在应用环节中,控制器需要应对有别于历史数据的实时风电场状态,因此,有必要提高控制器对输入数据的泛化能力。本文利用辍学层技术来减缓评价网络对历史数据的过拟合。
2.4 动作选择策略
动作选择策略根据所有可行动作的Q 值来选取最终的动作并作为控制器的输出指令。ε 贪婪策略为最普遍的动作选择策略,如式(8)所示。


3 深度强化学习的应用问题
将第2 章所述的深度强化学习算法应用到风电场储能系统预测决策一体化调度时,需要确定该应用背景下控制器(智能体)的状态空间、动作空间以及外部环境返回的奖励值。
3.1 状态空间
风电场的状态空间S 由前瞻电价λt+1、上一个调度时段结束后储能系统存储的电量值Et以及风电场的测量数据组成,如式(9)所示:

3.2 动作空间
在预测决策一体化调度模式下,控制器直接输出t+1 时刻储能系统需要完成的动作指令。因此,动作空间A 由储能系统的充放电功率值PESS,t+1的n 个等离散量ai组成,表达式为:
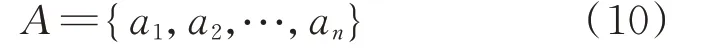
针对不同的风电场状态,控制器动态地在动作空间中选择能使风电场所获长期收益最高的动作。
3.3 奖励及目标函数
在学习环节中,深度强化学习算法需要根据外部环境返回的奖励值来确定控制器参数的更新方向与幅度。本文中,外部环境指电力市场环境下风电场收益的结算机制;奖励是风电场调度所获得的调度收益,计算式为:
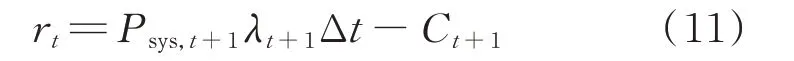
式中:Ct+1为风电场因储能系统运行状态越限而支付的惩罚费用。在深度强化学习中,用以更新控制器参数的奖励值被定义为一个与当前所处状态和所选取动作有关的随机值,这与因风电不确定性而导致的具有随机性的调度收益天然匹配。
控制器根据当前的风电场状态指导储能系统未来1 h 内的动作,该调度过程每小时进行一次。控制器每一次动作的目标是最大化风电场的长期收益,目标函数为:

式中:γ 为衰减系数。
3.4 储能系统的运行约束与惩罚费用
储能系统的调节能力受其运行约束的限制。本文以蓄电池组作为储能元件。储能系统的充放电功率可进一步表示为:

式中:Emax和Emin分别为储能系统允许的最大和最小存储电量值。
在当前工作中,为减少储能系统的运行损耗,储能系统每24 h 为一个调度周期,储能系统具有以下周期运行约束。
3)控制周期末时段电量约束

式中:E24为储能系统在一个控制周期结束后储能系统中存储的电量值;Eend为储能系统在进入下一个控制周期时要求的存储电量值,是一个固定值。该约束保证了储能系统能长期具备对风电场收益的调节能力。
4)储能系统充放电状态转换次数约束

式中:YESS,t值为0 表示t 时段与t-1 时段的充放电状态相同,值为1 表示状态发生了变化。
在调度过程中,若储能系统对式(19)和式(20)约束越限,风电场将根据越限程度来支付惩罚费用,惩罚费用计算如下。
1)违反控制周期末时段电量约束
违反该约束后,风电场以Eend与E24之间的差值为依据支付惩罚费用,表达式为:

2)违反储能系统充放电状态转换次数约束
违反该约束后,风电场以实际转换次数与最大允许转换次数的差值为依据支付惩罚费用,表达式为:

3.5 基于Rainbow 算法的风电场储能系统优化控制流程
基于Rainbow 算法的优化控制流程(包含学习环节与应用环节)及其实现方法见附录B。
4 算例分析
4.1 算例数据
本文以中国江苏省某装机容量为50 MW 的风电场为例,对所提方法进行分析和验证。风电场配备的蓄电池组参数如附录A 表A1 所示。储能系统在每个调度周期中充放电状态允许的最大转换次数为18 次,2 类系统越限后的惩罚费用系数均取1 000 元/MW。
风电场状态空间由前瞻电价λt+1、上一个调度时段结束后储能系统存储的电量值Et以及实时的风电场测量数据组成。测量数据包含:实时的测风塔10、30、50、70 m 处风速,轮毂高度的风速,测风塔10、30、50、70 m 处风向,轮毂高度的风向,风电场气压,湿度以及风力发电机的实时输出功率和15 min前的历史输出功率。整个状态空间由16 维数据组成。各时段的售电电价如附录A 表A2 所示。
动作空间中,储能系统的充放电功率被等间隔地离散为31 个动作,即{-7.5,-7.0,…,0,…,7.0,7.5}。
4.2 学习环节
评价网络结构如附录A 图A5 所示,该结构为含2 个隐藏层的全连接神经网络,输出层为竞争网络结构。神经元的激活函数为ReLU(rectified linear unit)函数。评价网络输入层的神经元个数与状态空间的维度相等,输出层的神经元个数与动作空间中可行动作的数量相等。
在评价网络的训练过程中,学习率α 取0.001;辍学层中的丢弃率取0.7;经验回放机制的样本存储量为3 000;时间差分偏差对取样概率的影响因子ω为0.6;每次小批量采样的规模为32;目标网络的更新间隔N 取300;奖励衰减系数γ 取0.9;ε 贪婪策略中ε 取0.1。
风电场收益随风电功率的波动而波动。风电场平均收益随控制器历经样本数量增加的变化曲线如图3 所示。图中蓝色曲线表示学习环节初期的样本积累阶段,该阶段中控制器经历样本的数量等于经验回放机制的样本存储容量(3 000)。在样本积累阶段中,由于样本的数量不足,Q 值的迭代和评价网络的训练未能被执行,造成该阶段的收益较低且无上升趋势。样本积累完毕后,从状态空间到动作空间的映射关系被持续优化,风电场的收益也随着历经样本的增加而有一个明显的上升阶段并随后达到稳定,该阶段平均收益为6 724.4 元/h。
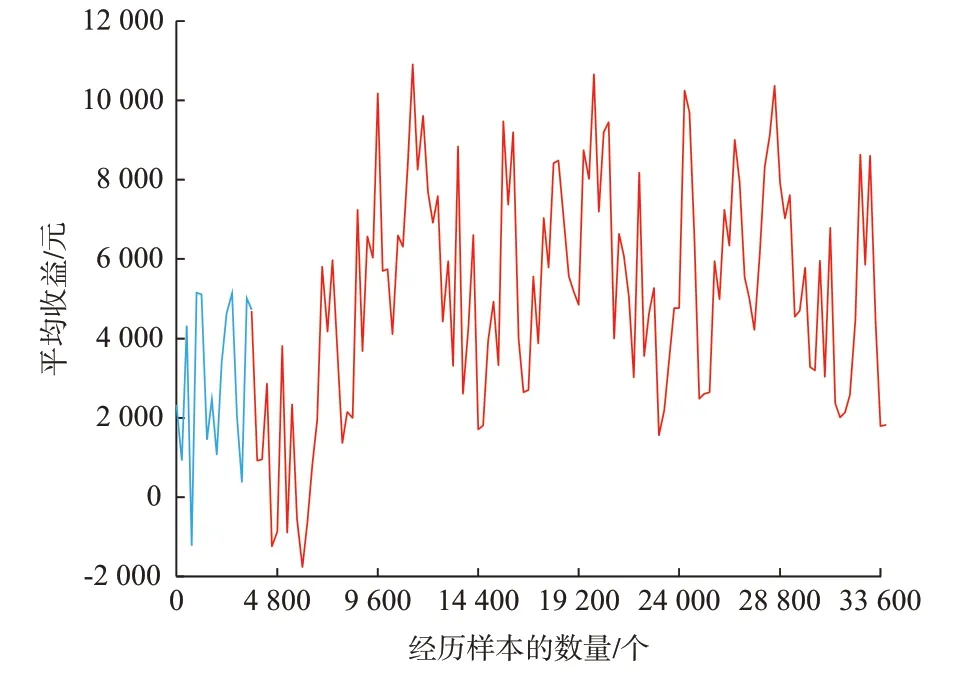
图3 风电场平均收益变化曲线Fig.3 Variation curve of average profit of wind farm
学习环节中风电场因储能系统状态越限而支付的惩罚费用如图4 所示。与风电场的收益相对应,惩罚费用也在波动中随历经样本的增加而减少并最终达到一个稳定的波动范围。

图4 惩罚费用变化曲线Fig.4 Variation curve of penalty cost
风电场所获收益、所支付的惩罚费用皆已趋于稳定,这代表评价网络的参数已收敛,可以被投入到模拟风电场实际运行场景的应用环节。
4.3 应用环节
应用环节使用该风电场中一组新的、时长为4 000 h 的测量数据来搭建控制器的在线运行环境。在学习环节中收敛的评价网络与贪婪策略组成了应用环节中的控制器。贪婪策略让控制器每次都选择选择Q 值最大的动作值作为输出指令,以获得最高的收益回报。风电场在应用环节中经调度所获得的平均收益增至7 207.6 元/h。
储能系统的波动曲线如图5 所示。可以看到,储能系统中存储的电量值能始终保持在适中的状态,避免了因电量达到存储的上下限而致使储能系统失去调节能力的情况。
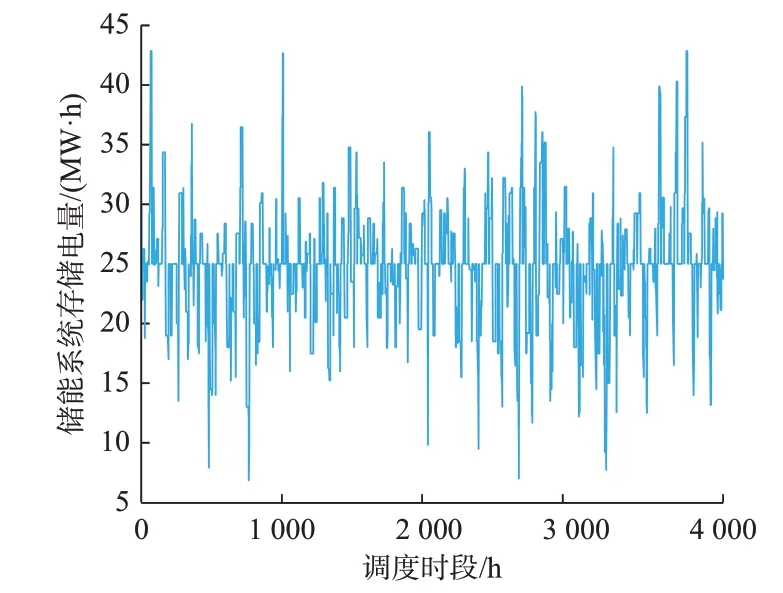
图5 储能系统内电量的变化曲线Fig.5 Variation curve of electricity in ESS
4.4 与传统调度方法的比较分析
为进一步说明所提方法的有效性,本文对预测、决策相分离的传统调度方法进行了比较分析,具体描述如下。
在预测阶段,风电场高维度的状态空间在经相关性分析、风电预测算法后得到前瞻的风电功率预测值。本文将功率预测值的平均绝对误差(mean absolute error,MAE)作为预测阶段的评价指标。
在决策阶段,控制器以风电功率预测值为决策依据来决策下一时刻储能系统的充放电功率值。在该阶段,风电不确定性体现在风电功率的预测误差上。分别使用Rainbow 算法和基于场景的随机规划(scenario-based stochastic programming,SSP)算法优化决策阶段的控制策略。优化过程中,Rainbow算法从风电功率的历史数据中挖掘不确定性规律进而优化策略;而在基于场景的随机优化过程中,风电功率的预测误差被假设服从正态分布N(μ,σ2),并取系数μ=0,σ=0.1yt,其中yt为t 时刻风电功率的预测值[26]。表1 给出了风电场经历4 000 h 运营后多种情况下的调度收益。

表1 多种情况下风电场的平均收益Table 1 Average profits of wind farm under different conditions
通过对比工况1 至6 或工况3 至6 可知,与传统调度模式相比,预测决策一体化调度模式能为风电场带来更高收益。一体化调度模式避免了因风电预测阶段而导致的决策信息的破坏与丢失,优化过程能充分利用蕴含在风电场高维度原始数据中完整的决策信息对控制器参数进行优化。
通过对比工况1 和2 或工况3 和4 可得:与数学优化算法相比,深度强化学习Rainbow 算法能更好地应对风电不确定性,优化结果更具经济性。原因在于:深度强化学习能使所建立的控制器可以很容易地统筹多时段系统的收益且无须人为假设风电的不确定性。
工况5 将风电的历史真值作为决策依据,给出该风电场理论上能达到的最高收益值。
综上,基于深度强化学习Rainbow 算法的预测决策一体化调度(工况6)兼具一体化调度模式和深度强化学习算法的2 种优势,所获调度收益也处于各种情况中的最高水平。
5 结语
本文提出基于深度强化学习的风电场储能系统预测决策一体化调度方法,以提升风电场在电力市场环境下的调度收益,结论如下。
1)提出预测决策一体化调度模式,通过将风电功率预测、储能系统动作决策2 个分离的阶段相融合,最大限度地避免了有效决策依据的丢失。
2)引入深度强化学习Rainbow 算法优化一体化调度模式下端到端的控制策略,所训练的控制器能动态地统筹多时段的系统收益。
3)通过与传统调度模式和数学优化算法的比较分析,表明本文方法能在风电不确定性条件下为风电场带来更高的调度收益。
本文的外部模型较为简单,在后续研究中,将致力于建立更接近真实电力市场的复杂外部环境并用于测试本文所提方法的泛化能力,这对将所提方法推广至实际应用十分重要。此外,本文所用Rainbow 算法属于基于值函数的深度强化学习算法,希望在后续研究中,将基于策略梯度的深度强化学习算法应用到风储控制中,实现输出动作的连续化。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

