含热电联产机组的分布式能源集群动态划分方法

潘明夷，刘 念，雷金勇

（1. 新能源电力系统国家重点实验室（华北电力大学）,北京市102206；2. 中国南方电网科学研究院有限责任公司,广东省广州市510080）

0 引言

随着分布式光伏和热电联产（combined heat and power,CHP）机组的大规模发展,形成了含CHP 机组的分布式能源网络,实现太阳能、电能、热能在社区/园区/商区层面的综合利用［1］。在市场因素的驱动下,分布式能源网络的商业模式呈多元化,多主体的参与、大量节点的接入导致传统的集中式调控难以满足需求［2］,含多主体的分布式优化已成为分布式能源网络优化调控的重要解决思路。根据可再生能源就地消纳和热能高效利用的基本原理,将分布式能源网络划分为若干个子区域,各子区域分别构成集群,可以充分发挥集群的自治特性,并实现集群间的协同优化运行［3-4］。因此,集群划分是实现分布式能源网络优化调控的基础环节。

集群划分的概念最早来源于复杂网络理论,近年来逐渐应用于含分布式电源的配电网,其应用场景包括优化调度［5］、电压控制［6］、优化规划［7-8］等。文献［5］以优化输电线路总损耗为目标,允许微电网主动合作并自我组织形成互不相交的微电网联盟分区,用以协调微电网之间以及微电网与大电网电站之间的电能传输。文献［6］考虑风电波动性对电气距离矩阵频繁变化的影响,构建全维空间电气距离矩阵,并以修正后的各潮流状态下电气距离之和作为分区依据,采用凝聚层次聚类方法实现电压分区。文献［7］提出了一种基于电气距离的模块度、无功平衡度和有功平衡度综合指标体系,利用改进遗传算法实现集群划分。文献［8］考虑光伏逆变器和储能装置解决电压越限的能力,在设计的综合性能指标基础上采用禁忌搜索算法确定集群划分方式,并基于分区结果配置分布式储能容量。文献［9］根据电力传输过程中的电气特性定义电气耦合强度矩阵,并以此为边权重建立加权网络模型,结合快速纽曼算法检测电网中的集群结构。文献［10］在节点间电压/电压灵敏度的基础上定义电气距离,并以基于电气距离的模块度指标为优化目标,利用改进粒子群算法实现无功电压分区。文献［11］以有功/无功-电压灵敏度矩阵定义电气距离,构建了基于电气距离的模块度和区域电压调节能力的综合性能指标,运用Tabu 搜索算法确定最优集群划分方式。文献［12-13］提出了一种考虑节点间无功电压灵敏度和区域无功平衡能力的改进模块度指标,自动形成最佳分区对配电网进行实时分区电压控制。从上述文献可以看出,针对复杂网络社区划分问题引入的模块度函数已逐步成为分布式发电集群划分的重要指标之一。

针对含CHP 机组的分布式能源网络,目前仍缺少相关的集群划分方法。而现有针对分布式发电的集群划分方法无法适用于分布式能源网络,主要原因包括3 个方面:①配电网转变为热电耦合的分布式能源网络,现有模块度函数中基于节点间电气耦合程度定义的网络边权重已不能合理量化分布式能源网络的集群特性；②现有集群划分指标主要围绕着节点间电气耦合程度展开,鲜少考虑节点间的功率匹配程度对集群划分的影响［14］,进而无法保证集群内部具有足够的能源供给能力以减少跨集群的能量流动；③由于CHP 通常运行在以热定电模式下,联产机组出力将受热能的限制,无法自主参与电能调度,从而降低了能源系统的整体调节能力［15］。

为解决上述问题,本文提出适用于分布式能源网络的集群划分指标:①根据电网和热网结构特性,定义计及电热网络特性的模块度指标,使得在电网和热网2 个层面上形成的集群在其内部联系紧密,集群之间联系松散；②为实现集群内部自我调节能力,划分时应保证集群提供的功率尽可能满足其内部用能需求,促进分布式能源就地消纳利用,定义供需匹配度指标；③由于源侧存在热电输出的耦合现象,在进行单一网络层面集群划分时,还应考虑源侧耦合出力和实际用能之间的平衡问题,定义热电耦合度指标。在集群划分指标的基础上,采用Louvain算法进行电网和热网2 个层面的集群划分。最后,通过算例验证所提方法的有效性与合理性。

1 集群划分指标体系

面向含CHP 机组的分布式能源集群划分方法主要通过发挥节点间的协调互补性,提高以热定电模式下集群内CHP 机组耦合出力和实际用能的匹配程度,以实现源荷合理匹配的目标,其评价指标可用热电耦合度指标表征。同时,所形成的电网和热网2 个层面的集群也应保证其内部具有足够的能源供应能力以及结构强度。据此,本文提出了以模块度指标、供需匹配度指标和热电耦合度指标为核心的集群划分指标体系。

1.1 计及电热网络特性的模块度指标

对于复杂网络中的分区问题,文献［16］提出使用模块度来衡量分区的质量并将其拓展到加权网络分区中。如果模块度较大,则意味着同一群落中的节点联系相对紧密,而不同群落中的节点联系相对松散。因此,模块度越大,表明划分的群落结构强度越大。模块度函数定义如下［17］:

对于涉及大规模电热能流交互的综合能源系统而言,由于系统内电能和热能传输分属不同的网络,彼此之间网络拓扑结构差异较大。因此,为保证所划集群逻辑与结构的合理性,权重矩阵A 应综合考虑电网和热网的结构性能进行定义。功率传输分布因子（power transfer distribution factor,PTDF）定义了节点之间传输功率变化时引起的各支路潮流的变化量［18］。假设系统中从节点i 到节点j 进行能量交易,线路l 的功率传输分布因子为［19］:

式中:fli和flj分别为功率从节点i 和节点j 注入并从参考节点流出,在线路l 上引起的潮流变化量。

由于在不同节点间进行电能传输时会不同程度引起各支路潮流的变化,影响整个系统的安全稳定运行。因此,可以基于不同节点间功率传输时引起的系统潮流变化量定义电网划分的权重矩阵,使产生的所有支路潮流变化量较小的划分至同一集群,变化量较高的划分至不同集群,从而确保系统在能量传输过程中的安全稳定运行。对于有l 条支路的网络而言,节点i 与节点j 之间进行功率传输引起系统的潮流变化FPij为:

在供热过程中,由于热水在管道内流动必然要克服阻力而引起能量损失,因此,可以根据节点间供热传输介质流动时产生的能量损失刻画热网分区的权重矩阵,将能量损失较小的划分至同一集群,能量损失较高的划分至不同集群,从而实现系统的经济运行。

管段长度为L 的沿程损失R 可以根据达西-维斯巴赫公式计算得到［20］:

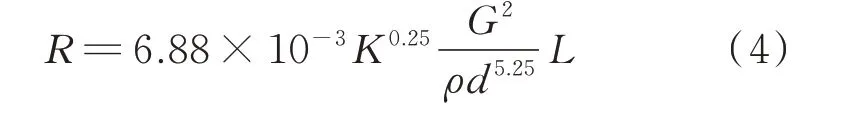
式中:K 为管道粗糙度；G 为流体流量；ρ 为流体的密度；d 为管道内径。

从式（4）可以看出,造成的能量损失与K,G,L成正比,与d 和ρ 成反比。因此为简化计算且不改变其含义,从节点i 到节点j 进行供热传输介质流动时,产生的能量损失可简化为:

1.2 供需匹配度指标

基于模块度指标进行集群划分仅能反映节点间的紧密联系程度,集群划分结果主要依赖于网络的拓扑结构,这样的划分结果显然是不合理的。CHP机组作为联系电力系统和热力系统的桥梁以及能源的主要来源,应保证在电网和热网2 个层面形成的集群内部能源供应能力尽可能满足用能需求,减少购能成本以及跨区域间的功率交换所造成的能量损失。引入供需匹配度指标,用以表征集群内CHP 提供的电功率或热功率与实际用能需求之间的匹配度。

供需匹配度指标不同于单一时刻属性的划分指标,是以待划分网络中节点的典型时变场景为基础进行描述的指标。为避免时变的负荷需求和电源出力对供需匹配度指标的影响,在计算时,首先计算集群各时刻的指标φk,t,然后根据集群在一定时间尺度下的特征,选取一定时间长度T 下的平均值进行集群划分,以更好地体现节点自身属性。对于电网层面的集群划分,供需匹配度指标为:

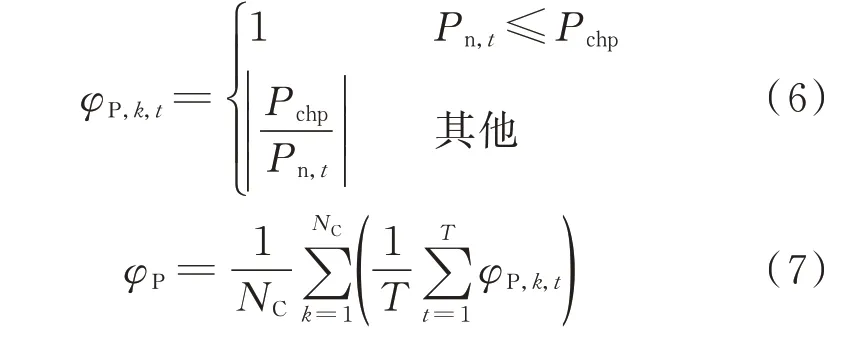
式中:φP,k,t为t 时刻第k 个集群提供的电功率与需求之间的匹配度指标；T 为调度周期；NC为集群个数；φP为整个网络的电功率供需匹配度指标；Pchp为集群内CHP 所能提供的电能最大值；Pn,t为t 时刻集群内所需电负荷。

考虑到热网传输存在的时间延迟,对于热网层面的集群划分,供需匹配度指标为:

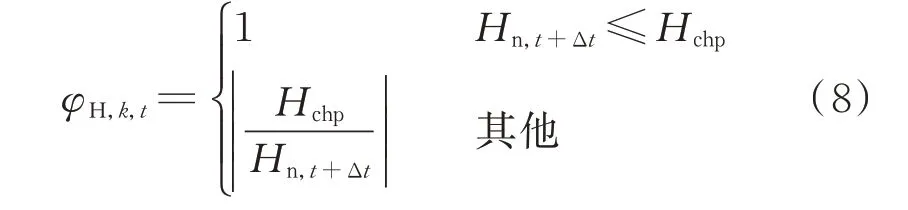
式中:φH,k,t为t 时刻第k 个集群的热功率匹配度指标；Δt 为热网传输的时间延迟；φH为整个网络的热功率匹配度指标；Hchp为集群内CHP 所能提供的热能最大值；Hn,t+Δt为t+Δt 时刻集群内所需热负荷；ηchp为微燃机的发电效率；ηL为散热损失率；δheat为制热系数。

1.3 热电耦合度指标

供需匹配度指标表征的是集群内源侧单一能源供应和实际需求之间的匹配程度,该指标在计算过程中仅涉及电或热单一网络。由于源侧热电输出的耦合现象,在进行电网层面集群划分时,还应考虑CHP 在对应热网集群内供能和实际用能的平衡问题,避免耦合侧能源产能过剩或供能不足,产生额外成本,影响系统经济运行。因此,增加热电耦合度指标,用以表征源侧耦合出力与实际用能间的偏差程度,该指标涉及CHP 所在电和热2 个网络。

热电耦合度指标是基于网络典型时变场景进行描述的指标:

式中:γP,k为第k 个电网集群的热电耦合度指标；M为电网集群内存在的CHP 个数；Pca,m,t为t 时刻电网集群内第m 个CHP 产生的富余或不足热功率部分；Hg,m,t为t 时刻该CHP 在当前电网集群划分下,根据集群内所需电能由于耦合作用实际产生的热能,由式（10）中Pchp=Pn,t计算得到；Hn,m,t+Δt为t+Δt 时刻该CHP 所在热网集群实际所需热能；γP为整个电网络的热电耦合度指标。

2 基于Louvain 算法的集群划分算法

2.1 算法分析

Louvain 算法以最大化整个社区网络的模块度函数为优化目标,能够在短时间内自动生成具有高模块度值的最优分区［21］。算法主要分为初始化、节点层面合并、社区层面合并3 个阶段。应用于集群划分问题的Louvain 社区检测算法,以最大化集群划分的优化目标来检测最佳集群划分结果。为实现以CHP 为中心的热电双重集群内部耦合出力与用能需求间的源荷合理匹配,本文依托第1 章提出的集群划分指标体系,分别设计适用于电网和热网2 个层面的Louvain 算法优化目标。

考虑到CHP 多运行在以热定电模式,即电力输出完全跟踪CHP 所在集群用热需求,因此,在初始热网和电网集群划分结果基础上,根据热网集群划分积极调整电网集群结构的需求更为迫切。首先,在保障所形成的集群内部节点紧密联系且集群供应能力满足内部需求的前提下,利用模块度指标和供需匹配度指标分别建立初始热网和电网层面集群划分的优化目标,可以得到单一网络层面的最优集群划分结果。集群划分结果一方面要保证集群内节点的联系强度,即模块度指标Q 值越大,集群内部联系越紧密,结构性能越好；另一方面要保证集群内部具备足够的能源供应能力,即供需匹配度指标φ 越大,集群内部能源供应能力越强,功能性能越好。初始热网集群划分的优化目标为:

然后,利用此划分方式得到的热网集群结果作为耦合网络的实际用热构建电网集群划分的热电耦合度指标,并结合初始电网集群划分的优化目标重新调整电网层面的集群结构。在保证集群结构强度和内部能源供应能力的基础上,调整电网集群结构,提高以CHP 为中心的热电双重集群内部耦合出力与实际用能间的源荷匹配程度,即热电耦合度指标γ 越大,表明耦合出力与实际用能间的偏差越小。用于调整电网集群划分的优化目标为:

2.2 算法步骤

对于一个含n 个节点的热电综合能源系统,实现电网和热网2 个层面集群划分的具体步骤如下。

步骤1:分别构建初始热网和电网层面集群划分的优化目标ρH,im=和ρP,im=。

步骤2:将综合能源系统中的每个节点都初始化为一个单独的集群,即集群数等于节点数。

步骤3:对于任意节点i,从其他节点中随机选择节点j 与其分别在热网和电网层面组合成新的集群CH(i,j)和CP(i,j)。为保证集群划分结果的逻辑性,利用邻接矩阵初步判断节点i 和节点j 所在热网以及电网层面集群是否存在直接连接。具有至少一个直接联系的2 个集群才有机会合并。

步骤4:计算合并前后的优化目标变化ΔρH,im和ΔρP,im,并 记 录 下max ΔρH,im和max ΔρP,im分 别 对 应的热网和电网层面集群编号。若max ΔρH,im＞0（max ΔρP,im＞0）,则 节 点i 选 择 加 入max ΔρH,im（max ΔρP,im）对应的节点j 所在的热网（电网）集群,否则保持不变。

步骤5:重复步骤3 和步骤4,直至所有节点所属热网集群和电网集群不再发生变化。

步骤6:对步骤5 发现的热网和电网集群结构分别进行压缩,将形成的集群看作一个新节点。

步骤7:返回步骤3,直到整个热网和电网的优化目标不再发生变化,集群划分过程停止,得到单一网络层面的最优集群划分结果。

步骤8:考虑源侧能量输出的耦合现象,对得到的初始电网集群划分结果进行调整。将热网集群划分下所需热能作为热电耦合度指标中耦合网络的实际用热,并结合模块度指标和供需匹配度指标重新构建用于调整电网层面集群划分的优化目标ρP,im=,热网层面集群划分的优化目标不变ρH,im=。

步骤9:重复步骤2 至步骤7,得到调整后的最优电网集群划分结果。

采用Louvain 算法实现集群划分的流程图如图1 所示。

3 算例分析

3.1 基础数据

通过一个由IEEE 69 节点的配电网络［22］和一个由文献［23］改进的69 节点热网组成的热电综合能源系统,验证了该方案的性能。该系统一共有69 个节点,其中热负荷节点69 个,电负荷节点69 个,含光伏电源节点69 个。CHP 装置联系电力网络和热力网络,分别在节点1,18,26,31,38,51,66 处加入。系统总的光伏出力及电、热、净负荷曲线如图2 所示,系统结构如图3 所示,CHP 参数设置如表1所示。

热力管道的传输延时与管道参数及热能传输距离有关,假设节点间距离每增加1 km,热网络传输延迟增加约1 h。因此根据本文所选取热网模型,设Δt=1 h。

图1 集群划分方法流程图Fig.1 Flow chart of cluster partition method

图2 总光伏输出功率以及负荷曲线Fig.2 Curves of total PV output power and load

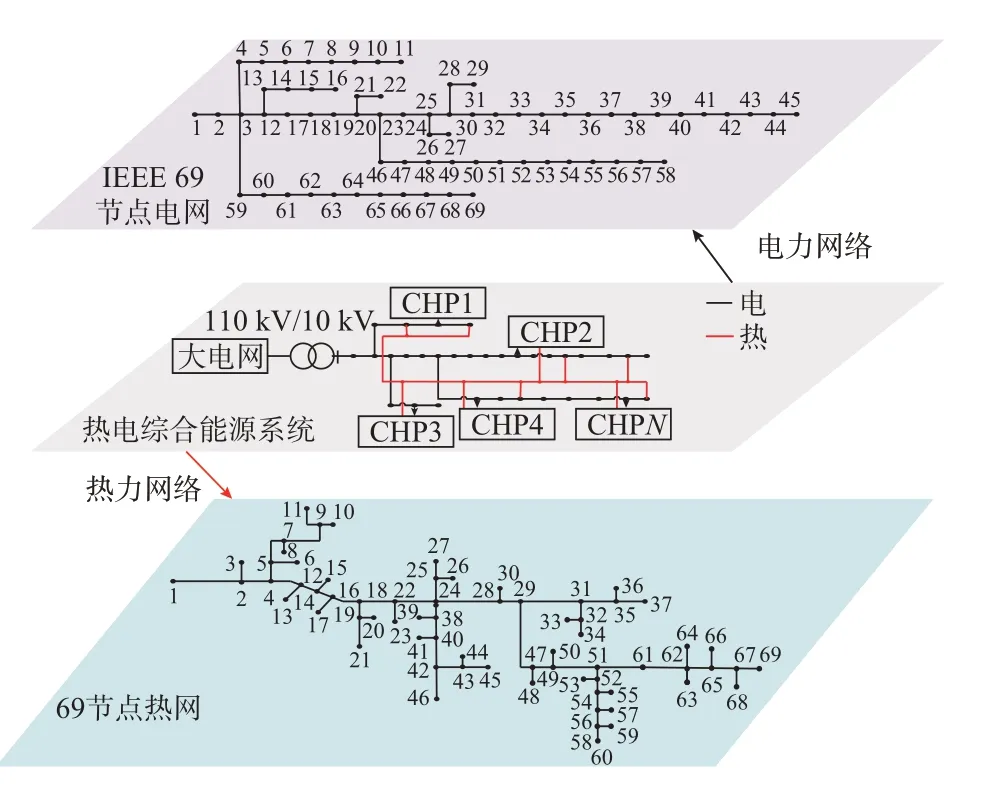
图3 综合能源系统结构Fig.3 System structure of integrated energy system

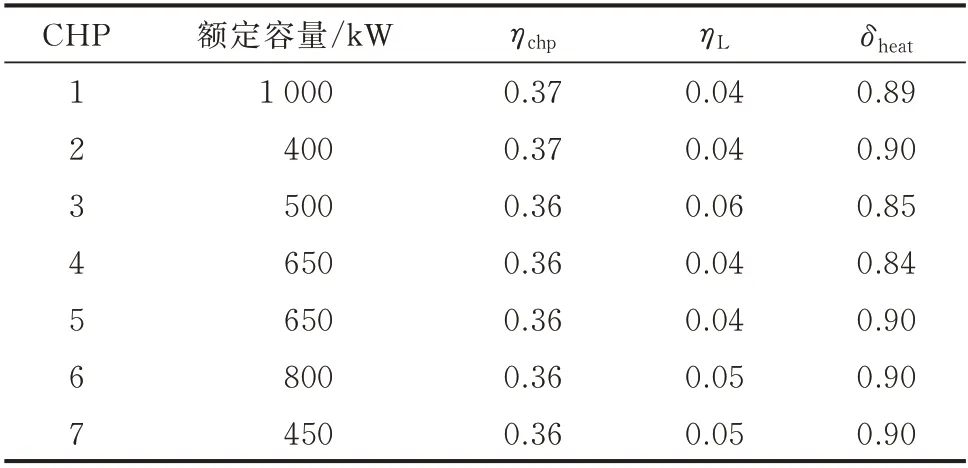
表1 各CHP 参数Table 1 Parameters of each CHP

3.2 集群划分结果分析

3.2.1 基于“模块度+供需匹配度”指标的初始集群划分

首先利用模块度指标Q 和供需匹配度指标φ 定义初始热网和电网集群划分的优化目标。为选取合适权重值得到单一网络层面最优集群划分结果,以进一步调整电网集群结构,本文根据指标重要程度选取不同的测试权重值w 得到相应的集群划分结果,通过比较分析在不同集群划分结果下各项指标的性能,最终选取各项指标均具有良好表现所对应的权重值作为最优权重值,相应的集群划分结果为最优集群划分方案。不同权重对应的集群划分结果如表2 所示。

表2 不同权重对集群划分的影响Table 2 Impact of different weights on cluster partition

从表2 可以看出:

1）电网/热网划分方案1:仅以模块度指标进行集群划分时,即w 均为0 时,Q 值最大,集群划分结果更侧重集群内部节点的联系紧密程度,结构性能良好。但由于其未考虑集群内部源荷协调性,相应的φ 值最小。

2）电网/热网划分方案2:当在模块度指标基础上增加供需匹配度指标作为集群划分的优化目标时,不仅考虑了网络的拓扑结构,而且还能够提高集群内源侧供能与实际用能需求之间的匹配程度,功能指标表现良好。

3）电网划分方案3:由于供需匹配度指标体现的是集群内节点间的协调互补特性,在划分过程中多以聚集节点的形式表现,因此随着供需匹配度权重的增加,如wP=0.8 时,可能会出现集群数目减少、单一集群规模过大、结构性能大幅下降的现象。

权重值的选取要兼顾系统功能性和结构性,即所选取权重值,既要保证ΔφP(ΔφH)有一定的增幅,又要确保ΔQP(ΔQH)减幅不至于过大造成结构性能大幅下降。通过上述分析,电网/热网划分方案2 可以满足系统对集群划分的要求,即选取wP和wH分别为0.4 和0.5 为最优权重值,对应的集群划分方案为最优集群划分方案,最后的集群划分结果如图4所示。由图4 可以看出,最终集群划分结果不存在孤立节点,集群满足连通性要求,各自模块度指标较大说明在网架结构和联系密切程度上性能良好。此外,φP=0.905 2 和φH=0.999 8 表明集群内CHP 可以较好地满足集群内用能需求,具有良好的供能能力。

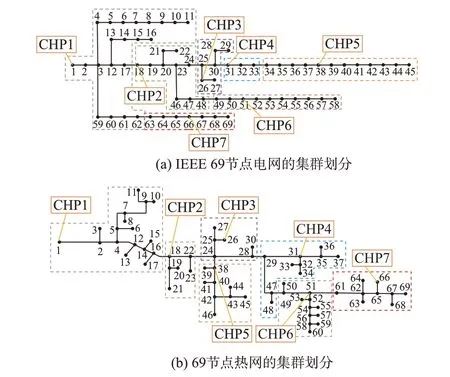
图4 初始集群划分结果Fig.4 Initial cluster partition result

3.2.2 基于“模块度+供需匹配度+热电耦合度”指标的集群结构调整

为进一步探究源侧耦合出力对集群划分造成的影响,在上述热网集群划分结果基础上,利用此划分方式得到的集群用热作为CHP 所在耦合网络的实际用热,并在初始电网集群划分的优化目标基础上叠加热电耦合度指标重新在电网层面进行集群划分,更新电网集群结果。而热网集群划分的优化目标不变,最终得到的集群划分结果保持不变。不同热电耦合度权重υP对电网集群结构调整的结果如表3 所示。

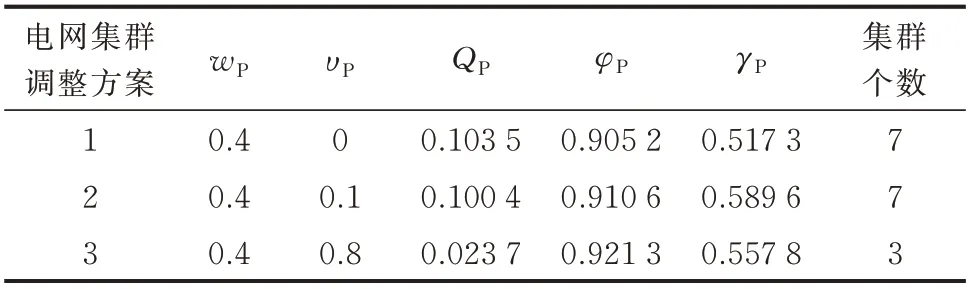
表3 不同权重对电网集群划分的影响Table 3 Impact of different weights on cluster partition of electrical network

从表3 可以看出,当加入热电耦合度指标后,在集群划分过程中也会根据耦合网络的实际用能情况,在确保自身网络结构和供应能力的前提下调整集群结构,以减少耦合输出功率与实际用能之间的偏差。但是随着热电耦合度权重增大,集群结构性能明显下降,其下降幅度甚至有可能远超热电耦合度增长幅度。如当υP=0.8 时,γP增幅为7.83%,而QP下降幅度将近80%。因此,选取υP=0.1 构建用于调整电网集群结构的优化目标。最后的集群划分结果如图5 所示。

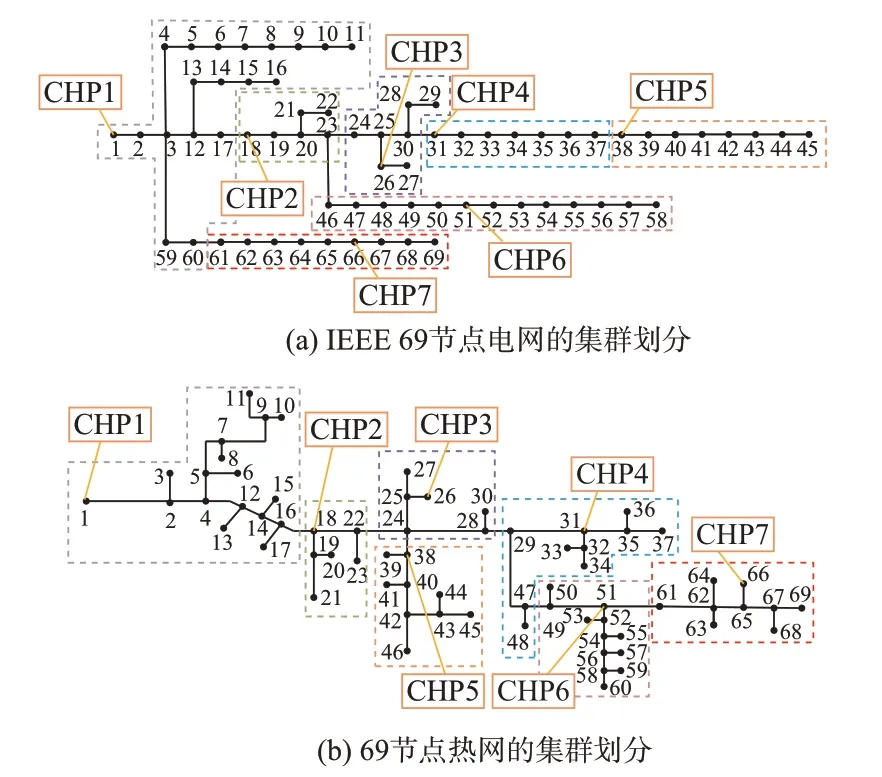
图5 经调整的集群划分结果Fig.5 Adjusted cluster partition result

3.2.3 集群划分结果的验证

随着分布式能源的快速发展,利用联盟博弈论的方法实现分布式能源网络间的合作,在缓解配电网中大电网的负荷波动以及减少输电线路上的功率损耗等方面具有重要意义［5,24］。本文所提出的集群划分最终形成了多个以CHP 为中心的热电联盟,在本质上可以看作是分布式能源网络多主体之间的一种新型合作策略。集群划分结果一方面要保证集群内部节点的紧密联系,另一方面要充分利用节点间功率的协调性,减少由于CHP 耦合出力与实际用能间的偏差,保障形成的以CHP 为中心的电热集群内部具备足够的自我调节能力,从而充分发挥集群的自治特性,避免跨集群的功率流动产生额外成本,影响系统的经济运行。

为验证本文所提集群划分指标体系及划分方法在实现区域自治方面的有效性,以CHP 发电成本和用能成本之和最低为目标函数,在采用不同集群划分指标所得集群结果基础上,进行以集群为单位的优化调度,并与采用集中式的从整体范围内进行的优化调度进行比较分析,结果如表4 所示。其中方案A 为基于“模块度”指标的单纯反映网络结构性能的集群划分；方案B 为基于“模块度+供需匹配度”指标所得初始集群划分；方案C 为本文所提基于“模块度+供需匹配度+热电耦合度”指标调整集群结构。三者集群划分结果分别对应附录A 图A1、图4 和图5。

表4 优化结果对比Table 4 Comparison of optimization results

从表4 中可以看出,以集群为单位调度总成本高于整体集中式调度总成本。但随着集群结构的调整,将热电耦合度指标纳入集群划分考虑因素之中,采用集群调度方式成本明显下降,且与全局调度方式相比,总成本计算精度可以达到98.72%,说明集群自治在优化调度上也可以产生与全局集中式调度近似的效果,体现了集群调度的有效性。此外,采用集群调度时,计算时间明显减少。这是由于集群划分可以将系统划分成若干个子区域,使网络对全局信息的搜索范围由原来的整个网络缩小到某一个分区,从而减少运行调度时间。尤其是当系统参与主体增多时,采用集群调度可以缓解系统的通信压力。

由表4 可知,方案A 集群调度结果总成本明显增大,经济性较差。这是由于基于模块度指标进行集群划分仅能反映节点间的紧密联系程度,集群划分结果主要依赖于网络的拓扑结构。一方面,由于未考虑集群内部能源供应能力,从附录A 图A1 中可以看出,并非所有热网集群内部存在CHP 供热,因而需要与外界进行热能交易以满足内部用热需求。另一方面,由于未考虑CHP 耦合出力与实际用能间的源荷匹配问题,受制于CHP 以热定电运行模式的刚性约束,系统内用电需求与CHP 发电量偏差较大,因此需要通过与电网交易平衡这部分功率,从而产生更多的额外成本。

对比方案B 和方案C 可以看出,在叠加热电耦合度指标以根据热网集群调整电网集群结构后,在CHP 出力基本保持一致的情况下,优化后系统与电网交易总量、总体运行成本均明显降低。这是由于在模块度指标和供需匹配度指标基础上加入热电耦合度指标进行集群划分,不仅考虑了集群的结构强度,而且注重集群内节点间的协调,通过优化集群的功率特性,提高CHP 耦合出力与实际用能间的匹配度,尽可能发挥集群自治特性实现集群内部能量的就地消纳,从而减少在优化过程中与电网的交易量,避免产生额外成本。

为进一步分析优化结果,以集群5 为例进行详细分析。初始集群划分和调整后集群划分中集群5的热能和电能优化调度结果如附录B 图B1 和图B2所示。考虑到热能传输延时,从附录B 图B1 中可以看出,在t 时刻产生的热能与t+1 时刻的热负荷一致。由于2 种划分方式下热网集群结果一致,CHP作为热能的主要来源,产热量相差不大,耦合作用产生的电量基本保持一致。但由于不考虑耦合度指标的集群划分结果未考虑CHP 耦合出力与实际用能间的源荷匹配问题,集群内部用电需求与CHP 发电量偏差较大,需要通过与电网交易平衡这部分功率,从而产生更多的额外成本。

4 结语

为合理利用集群结构解决综合能源系统的能量管理问题,本文以复杂网络社团结构理论为基础,综合考虑网络结构特性和节点间源荷匹配特性,提出结合模块度、供需匹配度和热电耦合度的集群划分指标体系,并据此构建优化目标在电网和热网2 个层面进行集群划分。所提划分方法能通过协调节点间的配合,在保证集群内部结构强度和供应能力的前提下,充分发挥集群内节点功率互补特性和调节能力,优化集群的功率特性,避免跨集群的功率流动产生不必要的成本,实现系统的经济运行。本文的不足之处是所提集群划分未考虑储能和蓄热装置对系统能源配置的影响,下一步的研究方向是分析增设储能和蓄热装置对集群划分产生的影响。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。