基于时空神经网络的风电场超短期风速预测模型

凡 航，张雪敏，梅生伟，杨忠良

（1. 清华大学电机工程与应用电子技术系,北京市100084；2. 电力系统及大型发电设备安全控制和仿真国家重点实验室,清华大学,北京市100084；3. 清华大学电子工程系,北京市100084）

0 引言

风能具有较强的随机性和不确定性。随着中国风电装机容量和比例的不断增高,风电消纳的难度逐渐增大,弃风问题日益凸显。提高风电场风电功率超短期预测的精度对电网在线优化调度具有重要的意义［1-2］。考虑“风速-功率”转换关系中的不确定性与风速不确定性的机理不同,因此有必要对两者分别进行研究。本文重点探讨如何提升风速超短期预测的精度,这也是进一步改进风电场功率预测精度的基础［3］。

超短期风电功率预测是指预测风电场未来0～4 h 的有功功率,时间分辨率不小于15 min［4］。相应的风速预测的时间尺度亦是如此。文献［5］提出了利用修正后自回归差分移动平均-广义自回归条件异方差（ARIMA-GARCH）模型进行超短期风速预测。文献［6］针对风速序列非线性、波动性的问题,首先利用变分模态分解将信号从低频到高频逐次分解,并对每个分量分别建立ARIMA-GARCH 模型再进行叠加。文献［7］在变分模态分解的基础上,分别采用后向传播的神经网络（BPNN）、自回归滑动平均（ARMA）模型和最小二乘支持向量机（LS-SVM）对高频、中频和低频信号进行预测。文献［8］采用了长短期记忆（LSTM）单元对风电场的超短期风速进行了预测,并在此基础上进行了功率预测。文献［9］在BPNN 中引入了误差校正环节。文献［10］提出风电场的风速之间存在较强的空间相关性,并给出了计及空间相关性的风速超短期预测方法。文献［11］采用了k 近邻进行空间相关性的超短期预测,并对预测模型的阶数、训练模型的样本容量与预测误差之间的关系进行了研究。文献［12］采用了最近历史观测值和偏最小二乘回归（PLSR）进行空间相关性超短期风速预测。

上述方法表明,风速超短期预测精度的提升在于获取更丰富的输入数据,并采用合适的方法建立预测模型。鉴于同一个风电场不同高度的风速和风向之间在时间和空间上都存在较强的相关性［13］,本文将利用这些实测数据改善风速在超短期尺度上的预测精度。同时,数值天气预报（NWP）技术的预测精度和更新时间的不断进步,将为进一步提升风速超短期预测精度提供便利［14］。文献［15］结合多重聚类和分层聚类方法对风电场的气象类型进行分类,并利用NWP 数据进行了超短期功率预测。

为了高效提取同一个风电场在不同高度的风速、风向历史数据以及NWP 数据的时空特征,本文引入了由卷积神经网络（CNN）和循环神经网络（RNN）组成的时空神经网络。CNN 具有局部连接和权值共享的特点,擅于提取数据的空间特征。RNN 采取递归的结构,能够提取数据的时序特性。由二者组合构成的深度时空神经网络在处理时序数据等方面取得了较大的突破和广泛的应用［16-18］。文献［17-18］根据城市交通流的相应物理特征信息设计了时空神经网络并将其应用到城市街道的人流和车流预测当中,取得了良好的效果。文献［19］采用CNN 和单向的门控循环单元（GRU）线性组合构建了时空网络,对风电场的功率进行了预测,但没有充分利用不同高度的风速、风向数据和NWP 数据。

因此,本文设计了一种新的时空神经网络对风电场的超短期风速进行了预测,能够充分挖掘风电场内不同高度风速、风向数据之间的时空相关性和NWP 的相关信息,并利用中国东北某风电场的实际数据验证了所提方法的有效性。

1 风速超短期预测的理论基础与数据描述

1.1 单风电场风速预测的时空相关性分析

传统单风电场的预测主要利用的是单风电场特定高度风速的时间相关性,结合机器学习算法或者深度学习算法对后续的风速进行预测。而风电场不同高度处的风速、风向受到区域内部大气运动的影响,存在较强的关联性［9］。这意味着,当前变量在某预测时刻的值,不仅仅与当前变量历史时刻的值相关,还与其他不同高度风速、风向的历史时刻取值相关。

风电场风速预测模型利用神经网络等模型对预测值与给定的历史信息变量之间的函数关系进行学习。传统的风电场风速预测只考虑了风电场风速未来时刻的输出和历史风速之间存在的耦合,具体可用式（1）来描述。

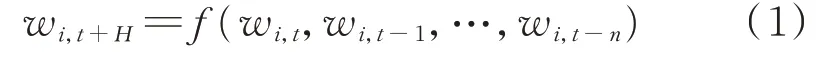
式中:wi,t+H为待预测变量i 在t+H 时刻的风速；wi,t为待预测变量i 在t 时刻的风速。

而预测算法本身是对这种变量之间的映射关系进行学习。可以看出,式（1）中的预测只考虑了单个变量的历史信息。而考虑了风电场时空相关性的预测指的是当前风电场的风速不仅与当前高度处的历史风速、风向相关,还与其他高度处的历史风速、风向以及NWP 数据存在一定的联系。可用式（2）来描述。

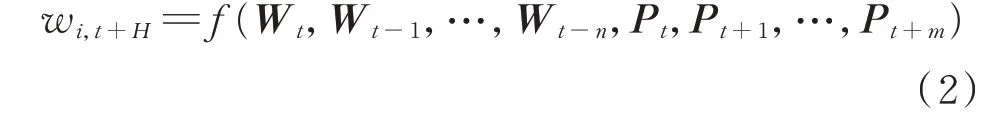
式中:Wt为t 时刻不同高度的风速、风向历史数据向量；Pt为t 时刻NWP 数据。

风电场的超短期预测需要对未来0～4 h 以每15 min 为时间间隔做预测。考虑到利用单步预测模型滚动16 次会带来误差的叠加,而4 h 内需预测的时刻数量并不太多。因此,本文针对0～4 h 的超短期预测是对每个时刻H 采用同样的网络结构分别训练的预测,一共可以得到16 个不同参数的预测模型。

1.2 风速超短期预测的时空数据描述

在风电场风速预测时,能够利用的信息有测风塔提供的不同高度的风速和风向信息。以东北某风电场为例,该风电场所能提供的数据包括10 m 风速、10 m 风向、50 m 风速、50 m 风向、70 m 风速和70 m 风向,而所需预测的是70 m 的风速。各高度的风速、风向之间存在着空间上的联系,而不同时刻的截面数据之间又存在着时间上的联系。因此,风电场的测量数据可以建模成时空数据。

在每个时刻,多高度的风速、风向数据构成一个向量。而随着时间的推移,这些按时间顺序采样得到的向量可构成一个矩阵。在进行样本集划分时,选取每个样本的长度为n。因为历史风速包含6 个不同的变量,所以每个样本为6×n 矩阵。

本文在预测中还考虑了NWP 数据。该数据来自中国电力科学研究院数值预报中心,原始的气象参数超过100 个。根据Granger 因果检验,选定了对风速预测最有价值的24 个变量（温度、动量通量、170 m 风速、100 m 风速、30 m 风速、10 m 风速、10 m海上风速、170 m 风向、100 m 风向、30 m 风向、10 m风向、10 m 海上风向、海平面气压、云量、潜热通量、感热通量、短波辐射、长波辐射、表面气压、总降水、大尺度降水、对流降水、2 m 温度和2 m 相对湿度）。当选取的NWP 时间窗的长度为m 时,每个样本为24×m 矩阵。

在实际的操作中,风速历史数据和NWP 数据属于不同类型的数据,在采样的时间间隔上也存在较大差异,而且状态变量之间都存在着时变的非线性关系。传统的统计和机器学习方法很难对其进行有效的刻画。因此,本文设计了以下时空神经网络,对风速和NWP 分别进行特征提取和特征融合。

2 基于时空神经网络的预测模型

2.1 考虑多元信息的时空神经网络模型

深度学习作为机器学习的一个重要的分支,能够通过构建更加深层和复杂的神经网络架构来提升对数据特征的提取能力。相较于传统的浅层神经网络,深度学习通过一系列非线性的数学变换,能够通过网状层级结构对数据中包含的深层次特征进行提取,从而进行分类或者预测。深度学习中通常用到的模块有CNN 和RNN。CNN 擅长提取数据的空间信息特征,RNN 擅长提取数据的时序特征信息。

在之前的研究中,有学者提出了将CNN 和GRU 进行拼接,从而搭建一个复合的网络进行研究的方法［16-19］。该网络在机器学习领域的研究中被称为时空神经网络。时空神经网络首先利用CNN 提取数据的空间特征,然后再利用LSTM 单元或者GRU 提取数据的时间维度特征,在人工智能领域的视频行为检测和分类任务中取得了良好的效果。但文献［19］采用的GRU 是单向的GRU,其只能提取到单向的特征。而CNN 提取特征并将其传递给RNN 之后,特征应该具有多维度的属性,如果只是利用单向GRU 进行回归,会损失掉部分有用的信息。因此,本文在文献［19］提出的时空神经网络的基础上,将单向GRU 替换成了双向GRU,从而更好地提取了数据的时序特征信息。在此基础上,提出了考虑NWP 数据的预测模型,如图1 所示。

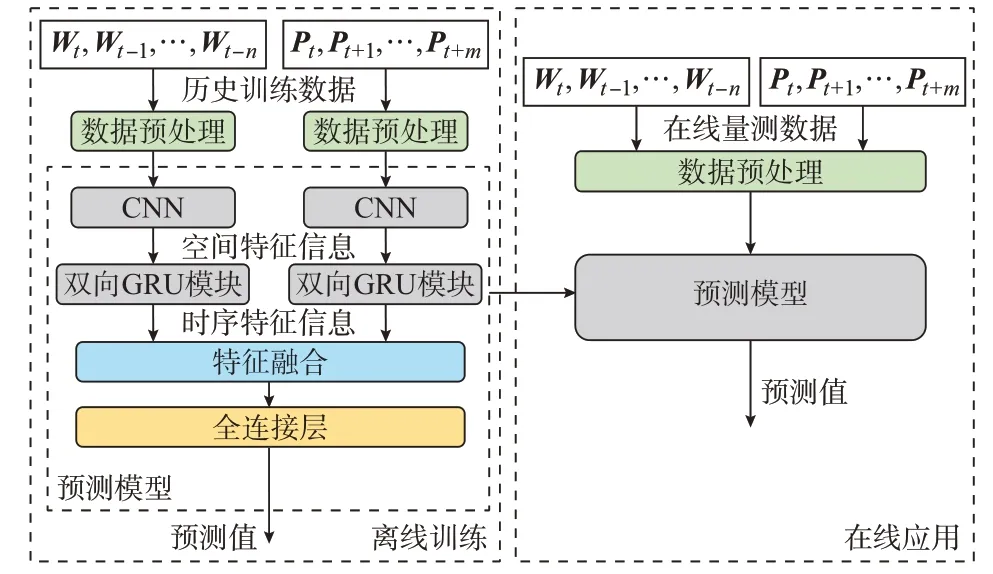
图1 考虑NWP 数据的时空神经网络模型Fig.1 Spatiotemporal neural network model considering NWP data

图1 中,考虑了NWP 数据的时空神经网络模型分为2 个部分。第1 个部分是离线训练部分,能够分别提取预处理后的历史风速数据和NWP 的空间信息,然后再将提取的空间特征分别传递到双向GRU 模块,提取时序信息。最后,再利用深度学习中经典的数据拼接的方式融合历史风速和NWP 的特征信息,并利用全连接层进行预测。而第2 个部分是模型的在线应用部分,能够将历史风速信息和NWP 数据进行相应的预处理,然后输入到训练好的网络中,快速给出预测的结果。

2.2 CNN 单元模块

本文利用不同大小卷积核的CNN 对风电场多变量之间的空间相关性进行了特征提取。图2 以历史风速数据为例进行说明。历史风速数据包含了10 m 风速、10 m 风向、50 m 风速、50 m 风向、70 m 风速和70 m 风向一共6 个变量。假设预测选取的样本时间长度为n,那么每个样本为6×n 矩阵。本文选取了含有3 组不同大小的卷积核的CNN 对输入数据的空间进行提取（卷积核的大小分别为6×k1,6×k2和6×k3）,其中每组卷积核的个数为N。再经过线性整流函数（ReLu）单元和1 维的池化（Maxpooling）操作之后,可以得到3 个相同长度的向量,通过对此进行直接的拼接,即为提取出的空间特征向量。在假定CNN 中步长（stride）等于1 的情况下绘制了示意图,如图2 所示。

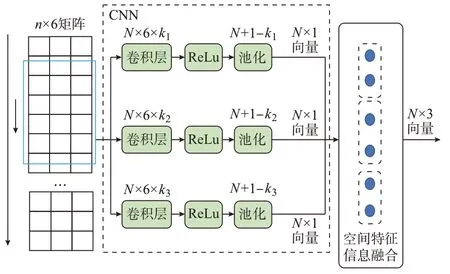
图2 空间特征提取模块示意图Fig.2 Schematic diagram of spatial feature extraction module

对于NWP 数据也可以进行同样的操作。对预测的wi,t+H,采用当前t 时刻之后的长度为m 的NWP 数据。NWP 数据中包含了24 种不同的状态变量。因此,对于卷积核的大小以及池化层的维度也需要分别进行相应的修改,从而得到N ×3 向量。

2.3 双向GRU 模块

RNN 擅长提取数据的时间信息特征,从而对序列数据进行分类或预测。在序列过长的时候,RNN在处理时可能会出现梯度耗散的问题。而且随着相关信息和预测位置的增长,RNN 很难处理这样的长期依赖问题。在RNN 的基础上,有学者提出了LSTM 单元。LSTM 单元通过一些“门”的设计能够有选择性地影响RNN 中每个时刻的状态。GRU网络是LSTM 网络的一种变体,因为GRU 网络把LSTM 网络中的遗忘门和输入门用更新门代替了,其结构相比于LSTM 网络的结构更加简单,而且效果也更好。GRU 网络中单元状态（cell state）和隐藏状态（hidden state）进行了合并,计算当前时刻信息的方法和LSTM 网络有所不同［19］。GRU 网络包含了重置门、更新门、候选记忆单元和当前时刻记忆单元4 个单元,其计算分别如式（3）—式（6）所示。

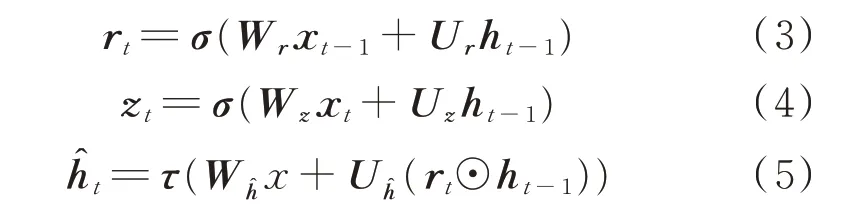
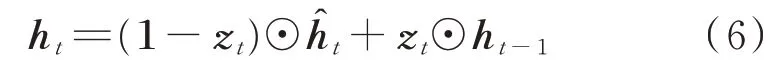
式中:xt为输入向量；rt,zt,ht分别为重置门、更新门、候选记忆单元和当前时刻记忆单元向量；Wr和Ur为重置门参数；Wz和Uz为更新门参数；Whˆ和Uhˆ为候选记忆单元的参数；σ(⋅)和τ(⋅)表示激活函数；“☉”表示向量元素依次相乘。

在经典的RNN、LSTM 网络和GRU 网络当中,状态的传输是从前往后单向的,因此只能提取数据在一个方向上的特征。但是在许多序列的预测或者分类任务中,当前时刻的输出不仅和之前的数据相关,而且和之后的数据也紧密关联［20-21］。所以,需要利用双向的网络,因此在此基础上衍生出了双向RNN、双向LSTM 网络和双向GRU 网络。

文献［22］提出了在风功率预测中的双向预测机制。因为用于风速预测的数据,在经历了CNN 部分的特征提取之后,传递给了RNN,如果只用单向GRU 去提取特征,只能提取到单向的信息,不能准确地实现特征提取。而且,本文在进行风功率预测的时候,利用了未来时刻的NWP 信息,数据具有相应的反向相关性。因此,本文在提取时序特征的时候,采用了双向GRU 网络。一方面,能够对长序列的时序特征进行提取,而不出现梯度耗散的问题,另一方面,也能够捕捉到序列的双向特征,如图3所示。

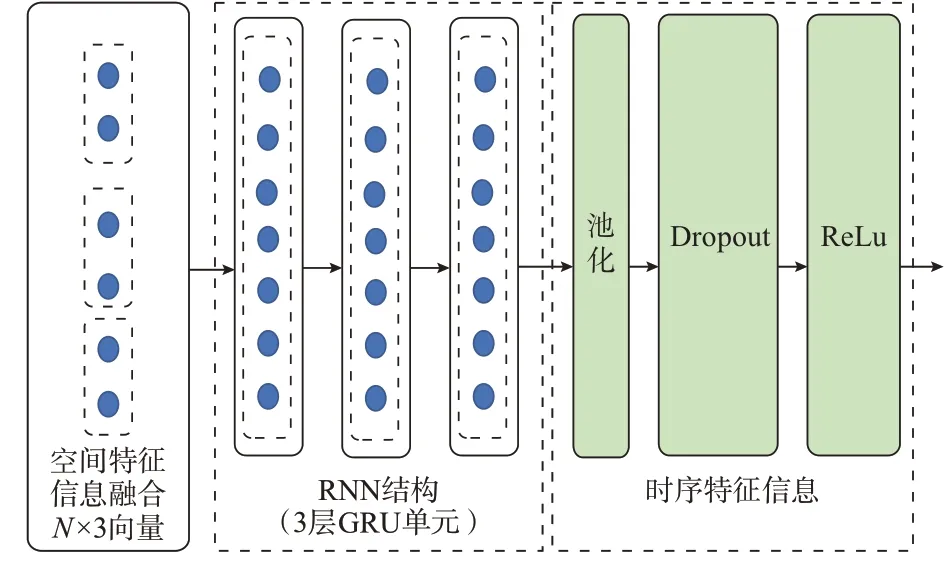
图3 时序特征提取模块示意图Fig.3 Schematic diagram of temporal feature extraction module

2.4 特征融合和训练算法

特征融合是指把不同数据源的特征进行合并。利用Concatenate 方法对网络结构进行特征融合在机器学习中是一种经典的操作,在DenseNet 和U-net 中都采用了相应的方式进行特征融合［23-24］。文献［25］采用了时空网络对出租车的需求量进行了预测,并将地理信息和时序信息进行了Concatenate 融合。本文采用了文献［25］中的特征融合办法,对于分别通过CNN 和双向GRU 网络提取出的风速、风向历史数据和NWP 数据的2 个特征向量进行拼接,得到1 个向量,再将其输入全连接层,即可得到预测的结果。

用神经网络的方法对风电场的风速进行训练的过程本质上是对式（2）中的函数f 进行最优的逼近,需要求解优化问题,而训练过程也就是对优化问题的求解过程。常见的机器学习优化算法包括随机梯度下降（stochastic gradient descent,SGD）算法、Momentum 算 法、Nesterov Momentum 算 法 以 及Adam 算法等。因为Adam 算法能够对学习率进行自适应调节,在众多深度学习的任务中取得了较好的效果,本文选用Adam 算法进行训练,其参数更新的具体机制可参见文献［26］。

3 测试算例

本文采用了中国东北某风电场的实际数据作为测试算例,对所提方法进行了测试。其中深度学习的算例在Linux 系统服务器集群进行测试,采用了Pytorch 框架。

3.1 数据集和模型结构说明

本文选取了东北某额定容量为45 MW 的风电场作为测试系统。

测风塔测量数据时间间隔为5 min,包含10 m风速、10 m 风向、50 m 风速、50 m 风向、70 m 风速和70 m 风向。NWP 数据的时间间隔为15 min,包含了温度、动量通量、30 m 风向等24 个变量。采用某年1 月份的数据用于训练和测试,整个数据集中前80%的数据作为训练集,后20%的数据作为测试集。例如:测风塔1 个月的数据共8 640 个样本。其中前7 000 个样本作为训练集,后1 640 个样本作为测试集进行试验。

因为风电场风速的超短期预测要求时间分辨率不低于15 min,本文采用每15 min 一个点的单步预测方式,分别设计了16 个模型对0～4 h 的超短期风速进行预测。

风向数据的实际测量中,风向在360°和0°之间波动,由此导致风向的时序数据呈现出不连续的特性。因此,对风向角度在50°以下的数据认为是上一次波动的结果,故在此基础上增加360°,并将异常值除去。

因为风速的测量具有不同的量纲,为了减少量纲和变量类型不同对预测结果的影响,采用式（7）对风速、风向进行归一化。

式中:xe为标准化之后的模型输入数据；xs为原始的输入数据；xmax和xmin分别为原始数据的最大值和最小值。

为了更加直观有效地对预测方法进行准确评估,本文定义了4 种误差评估指标,分别为均方根误差、平均绝对误差、归一化的均方根误差和归一化的平均绝对误差,其表达式分别为:

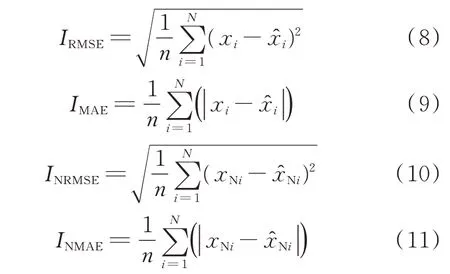
式 中:xi和ˆ 分 别 为 真 实 值 和 预 测 值；xNi和分 别为归一化之后的真实值和预测值；IRMSE和IMAE分别为未经归一化的均方根误差和平均绝对误差；INRMSE和INMAE分别为归一化之后的均方根误差和平均绝对误差。

本部分利用时空神经网络对单个风电场进行风速预测。经过对模型结构以及参数的调整,最终模型的参数如下。

1）CNN 层:CNN 中包含了3 组不同大小的卷积核。第1 组卷积核大小为3×6 向量,第2 组卷积核大小为5×6 向量,第3 组卷积核大小为7×6 向量。激活函数都为ReLu,每组包含了60 个卷积核。

2）双向GRU 层:采用3 层的双向GRU 网络,其中隐藏节点的数目为90 个。

3）Dropout 层:为避免过拟合,按照一定概率对网络中的隐含神经元进行随机丢弃,本文选用的概率为0.2。

4）全连接层:连续2 个单一神经网络的全连接层作为时空神经网络的输出层,输出的结果即为t 时刻风速的预测值。

模型训练的时候迭代次数为100 次,并采用5 折交叉检验的方式进行验证。

3.2 不同预测算法的性能比较

为了验证本文所提方法的有效性,下面对既采用双向GRU 网络又引入了NWP 数据的时空神经网络模型（用STNN2 表示）、采用了双向GRU 网络但不考虑NWP 数据的时空神经网络（用STNN1 表示）与其他比较典型的风速超短期预测模型的误差进行对比。以未来4 h 的风速预测为例,式（8）—式（11）中定义的4 种误差指标的结果如表1 所示。

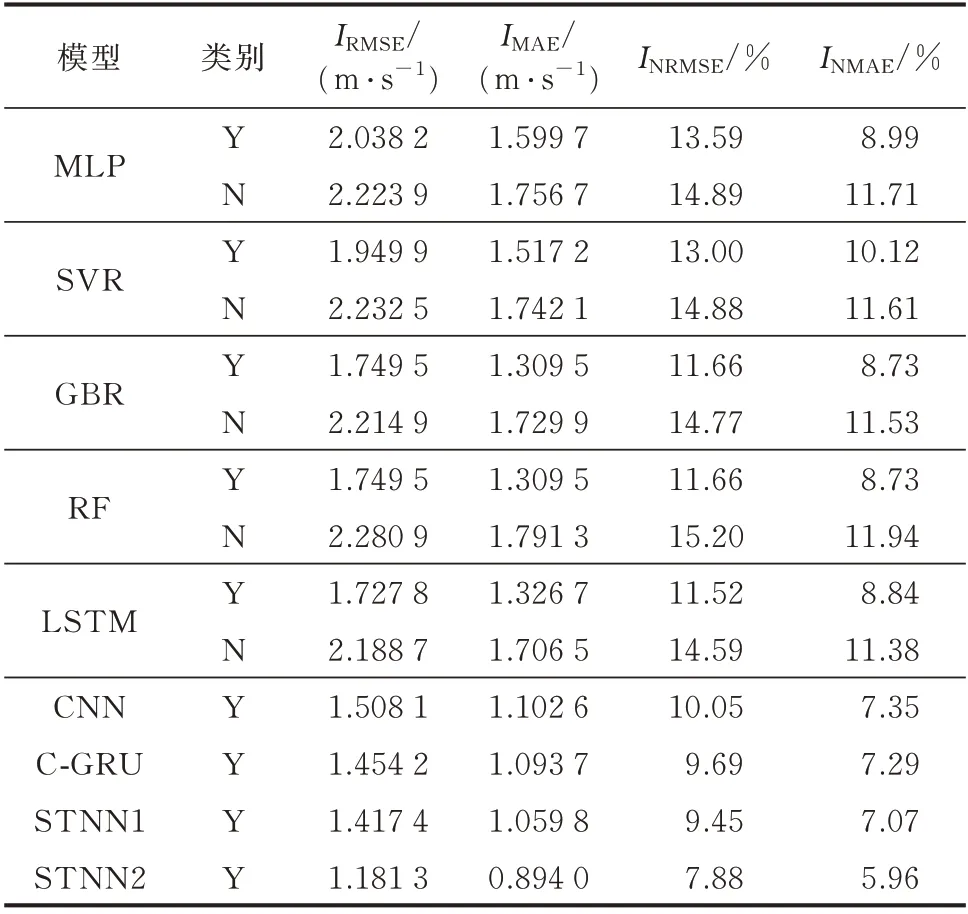
表1 不同预测方法的性能比较Table 1 Performance comparison of different prediction methods

表1 中,MLP,SVR,GBR,RF 和C-GRU 分 别表示多层感知器、支持向量回归、梯度提升回归、随机森林和文献［19］中设计的网络；Y 和N 分别表示考虑了不同高度、风速、风向相关性的模型和不考虑不同高度、风速、风向相关性的模型。表1 中的数据说明,通过引入不同高度的风速、风向数据,能够提高预测的精度。同时,时空神经网络（STNN1 和STNN2）相比于传统的机器学习算法和简单的CNN 以及LSTM 网络具有更高的预测性能。而且通过在STNN1 中增加NWP 的信息,STNN2 能够进一步地提升预测的精度。

3.3 不同预测算法与预测时间的相关性研究

在超短期预测中,3～4 h 的预测精度往往比1 h以内的精度更难以提升。 图4 比较了CNN,LSTM,SVR,GBR,RF,MLP,C-GRU,STNN1,STNN2 在不同预测时间下的性能。

由图4 可见,各方法的预测误差都随着预测时间的增加而增加。但是,计及了NWP 信息的时空神经网络STNN2 在各个时段的预测性能均优于其他预测,且误差增长较慢,因此可以说明本文在对数据的输入维度和预测方法层面进行改进后,能够有效提升预测精度。本文也对NWP、实测风速的误差以及对预测性能的影响做了分析,详细结果可参见附录A。当前实验结果中NWP 与实测风速误差在1.9～2.7 m/s 之间。可见,本文算法得到的风速预测误差比NWP 的误差降低了大约1 m/s。

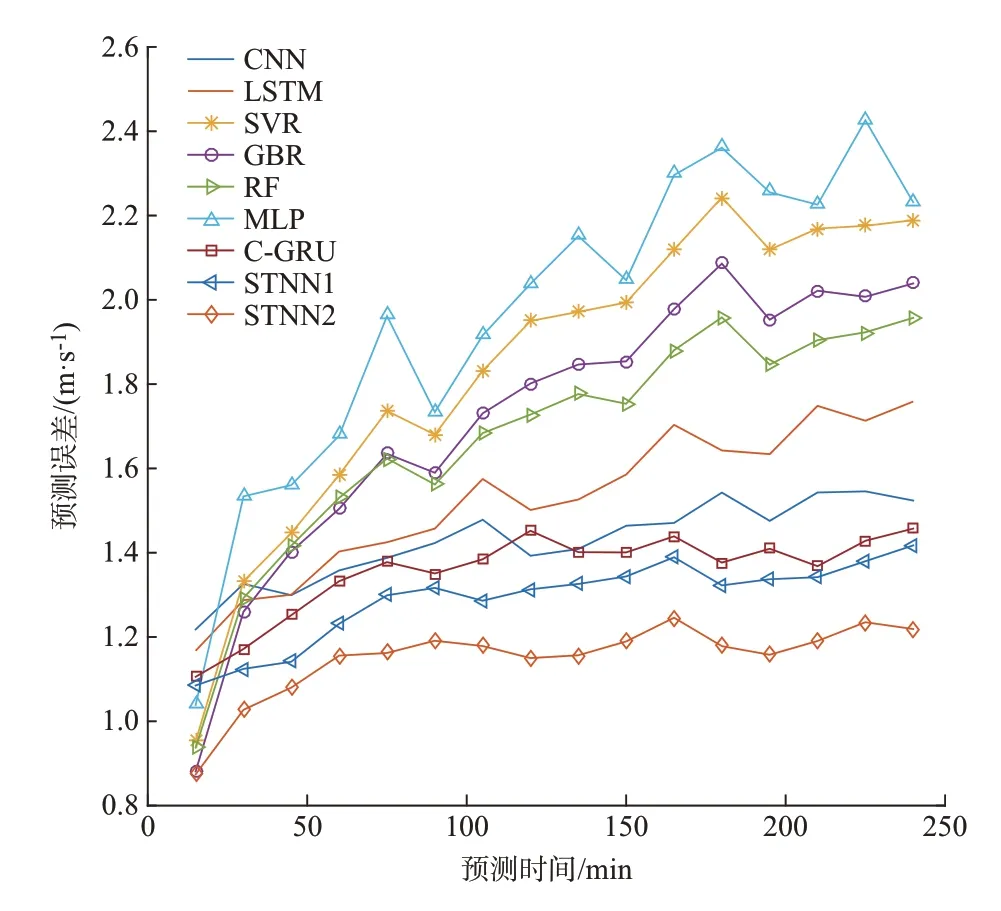
图4 预测误差随时间变化图Fig.4 Variation diagram of prediction error with different time scales

3.4 网络预测性能与参数相关性研究

CNN 的预测性能和Adam 算法中学习率初始值、隐藏层数目及GRU 层数等参数紧密相关。通过分析可以发现,学习率对预测结果的影响较大,而隐藏层数目和GRU 层数对预测结果的影响较小。从整体上来说,包含了NWP 数据的预测模型的预测性能在各种参数下的预测性能均优于不含NWP 数据的情形。模型参数的灵敏度分析结果见附录B。

3.5 预测精度与输入数据时间长度之间的联系

考虑到预测精度与输入数据的时间长度紧密关联,本文选取了不同长度的数据对风电场的风速进行预测。历史数据的输入数据的时间长度分别为20、30 和40（即100,150,200 min）,NWP 数 据 的时间长度固定为20（即100 min）。以未来3 h 的风速预测为例,表2 给出了输入数据长度与预测误差的关系。

由表2 的结果可以看出,在不同的输入数据长度下,计及NWP 信息的时空神经网络STNN2 的预测模型的精度均高于其他几种预测模型。而且随着输入数据的长度增加,预测精度逐渐提升。但在实际操作过程中,当输入数据的长度为20 时,训练耗时为839.48 s。当输入数据的长度为40 时,训练耗时为2 133.10 s。鉴于训练模型并不需要频繁更新,这一速度基本能满足要求。

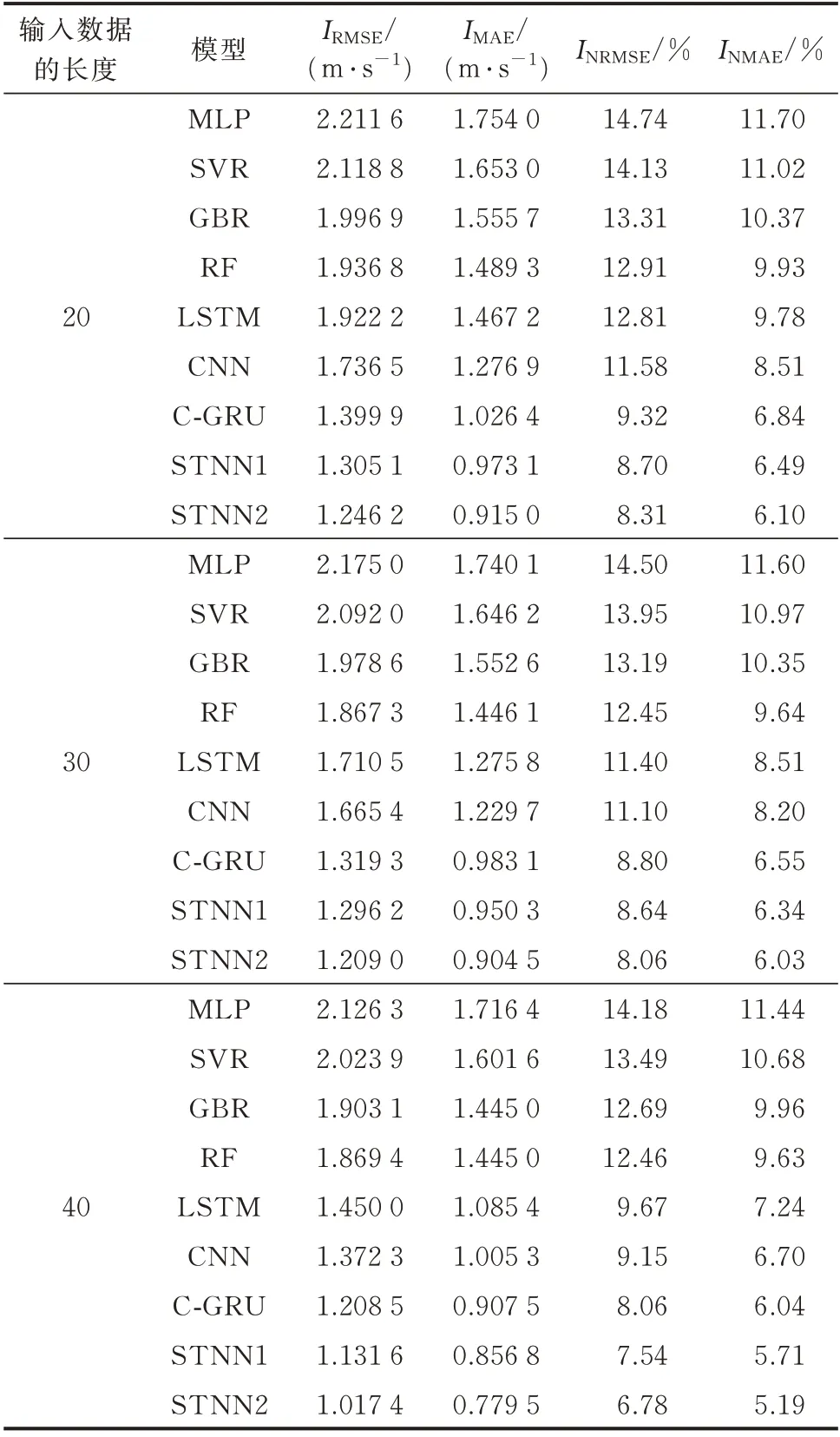
表2 不同预测方法在不同输入数据长度下的性能比较Table 2 Performance comparison of different prediction methods with different lengths of input data

4 结语

本文提出了一种基于时空神经网络的超短期风速预测方法。算例分析表明,该方法能够充分利用不同高度的风速、风向数据和NWP 数据中的时空相关性,有效提升了风电场超短期风速预测的精度。

在后续的研究中,将把该时空网络拓展到多风电场风速预测的研究中,以进一步提升预测的精度。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。