100%低地板齿轮箱振动分析及噪声预估

彭锐涛，谢炎培，罗秀强，胡聪芳，刘祥环

100%低地板齿轮箱振动分析及噪声预估

彭锐涛，谢炎培，罗秀强，胡聪芳，刘祥环

(湘潭大学 机械工程学院，湖南 湘潭 411105)

对100%低地板齿轮箱进行振动分析和噪声预估，可为其设计及优化提供依据。建立了传动系统和结构系统相耦合的100%低地板齿轮箱刚柔耦合多体动力学模型，获得了轴承支反力；建立了齿轮箱模态分析模型，研究了箱体的振动特性。基于相似性理论设计了箱体的相似模型并对其进行了实验模态分析，验证了有限元模型的正确。将刚柔耦合多体动力学仿真获得的轴承支反力作为箱体的激励，采用直接积分法计算箱体的振动响应；以箱体振动速度作为边界条件，建立了齿轮箱直接边界元法辐射噪声分析模型，进行齿轮箱表面声压及外声场辐射噪声预估。结果表明：齿轮箱辐射噪声频域曲线的噪声峰值频率出现在齿轮副啮合频率及其谐波，以及箱体低阶固有频率处。

100%低地板；齿轮箱；刚柔耦合动力学；振动特性；相似性理论；辐射噪声

低地板轨道交通系统属于中等运输量的交通方式，填补了当前公共交通方式运量的空白，同时具有节能环保、舒适安全、建造价格低、便于乘客上下车和兼具城市观光功能等优点，适合用作大城市的支线交通[1−2]。因此，低地板轨道交通系统这种新型的城市交通运输形式，正受到越来越多的关注和欢迎。100%低地板轨道交通系统由于整车地板平面距离轨道平面高度在400 mm以下，所以可用于安装车辆设备的空间狭小[3]。100%低地板轨道交通系统传递动力采用的方式是使用齿轮箱直接驱动车轮，其齿轮箱的结构具有占用空间小、外形紧凑的特点。100%低地板轨道交通系统的低地板结构特点使齿轮箱这个重要的噪声源离车厢内乘客的距离变近，并且轻量化的车体设计以及玻璃材料的大量使用使得车辆的隔声能力变得更加薄弱，这对100%低地板轨道交通齿轮箱的振动及噪声控制性能提出了更高的要求[4]。车辆运行过程中齿轮箱的振动及噪声不仅会影响齿轮箱的使用寿命，而且也会影响乘客的乘坐体验[5−6]。因此对齿轮箱开展振动及噪声性能的研究是100%低地板轨道交通系统设计的一项重要研究内容。众多的学者对齿轮箱的振动及噪声性能进行了深入研究。ZHOU等[7−8]分析了齿轮传动系统的内部激励，获得了轴承力，并将其作为箱体的激励，进行瞬态动力学分析获得了箱体的振动响应。林腾蛟等[9]建立了船用齿轮箱的多刚体动力学模型，运用边界元法预估了齿轮箱的辐射噪声。陆波等[10]将某大型船用齿轮箱的传动系统和结构系统耦合了起来，综合考虑系统内部激励和外部激励进行齿轮箱的结构噪声预估。任亚峰等[11]研究了箱体的柔性对齿轮传动系统动态特性的影响。Abbes等[12]考虑齿轮副的时变啮合刚度，使用声固耦合方法开展了齿轮箱辐射噪声的分析。但是考虑箱体的柔性以及传动系统和结构系统的耦合作用进行齿轮箱振动及辐射噪声研究并进行试验验证的文献较少。本文建立了结构系统与传动系统相耦合的100%低地板齿轮箱刚柔耦合多体动力学模型，获得了轴承支反力；而后对箱体进行有限元模态分析，分析箱体的振动特性。基于相似性理论设计了箱体相似模型，采用3D打印技术制作了相似模型，并对其进行实验模态分析验证有限元模型的正确性。将轴承支反力加载到箱体轴承座位置，使用直接积分法计算箱体的振动响应；建立100%低地板齿轮箱直接边界元法辐射噪声分析模型，将获得的箱体振动响应作为边界条件进行齿轮箱表面声压及辐射噪声预估。

1 刚柔耦合多体动力学

1.1 齿轮箱三维建模

100%低地板齿轮箱的传动系统由三级齿轮传动组成，输入级是锥齿轮传动、中间级和输出级是斜齿轮传动。在表1中列出了齿轮箱各传动级齿轮齿数。在SolidWorks软件中建立了齿轮箱的三维模型，如图1所示。传动系统中齿轮和轴的材料为18CrNiMo7，其弹性模量为1.9×1011Pa，密度为7 800 kg/m³，泊松比为0.30；结构系统的材料为QT400-18，其密度为7 000 kg/m³，弹性模量为2.0×105MPa，泊松比为0.32。

表1 齿轮箱齿数

图1 100%低地板齿轮箱模型

1.2 约束和载荷

根据齿轮箱各部件间的运动关系，在Adams软件中建立结构系统和传动系统相耦合的刚柔耦合多体动力学模型，使用轴承单元将刚性传动系统与柔性结构系统连接。图2为所建立的齿轮箱刚柔耦合多体动力学模型。

图2 刚柔耦合模型

根据100%低地板齿轮箱的实际运行工况，定义输入轴的输入转速为2 100 r/min，负载力矩为3 068.4 N«m。ADAMS软件采用冲击函数法计算法向接触力，采用库仑摩擦方法计算切向接触力。输入级齿轮副的刚度系数为4.805×105N/mm，中间级齿轮副的刚度系数为7.933×105N/mm，输出级齿轮副的刚度系数为1.096×106N/mm。阻尼系数通常取刚度系数的0.1%～1%，这里取0.1%。根据齿轮对的材料属性选取非线性弹簧力指数为1.5，最大穿透深度为0.1 mm。

图3 X方向轴承支反力

1.3 刚柔耦合动力学仿真

使用STEP函数定义转速以及负载扭矩在0～0.1 s时间段从0开始递增，设置仿真时间为0.5 s，进行齿轮箱刚柔耦合动力学仿真。输出轴最外侧轴承方向的轴承支反力如图3所示。仿真获得了9个轴承的轴承支反力，并对仿真结果提取0.1～0.5 s稳定阶段轴承支反力，将其作为箱体动力学仿真的激励。

2 齿轮箱箱体振动特性分析

2.1 有限元模型

从低地板齿轮箱的三维模型可知箱体结构比较复杂，考虑到计算效率和网格划分难度等问题，需要对导入ABAQUS软件的箱体模型进行一定程度的简化，以此来降低网格划分的难度、改善网格质量和提高有限元软件的运算效率。对箱体的小圆角、小孔、小凸台等对齿轮箱箱体整体质量和刚度影响较小的一些特征进行简化。同时在建立齿轮箱箱体模型时，不考虑左右箱体结合部、轴承端盖与箱体结合部的影响[13]。使用自由网格划分方式直接进行箱体的网格划分，共计单元49 364个，节点87 629个。

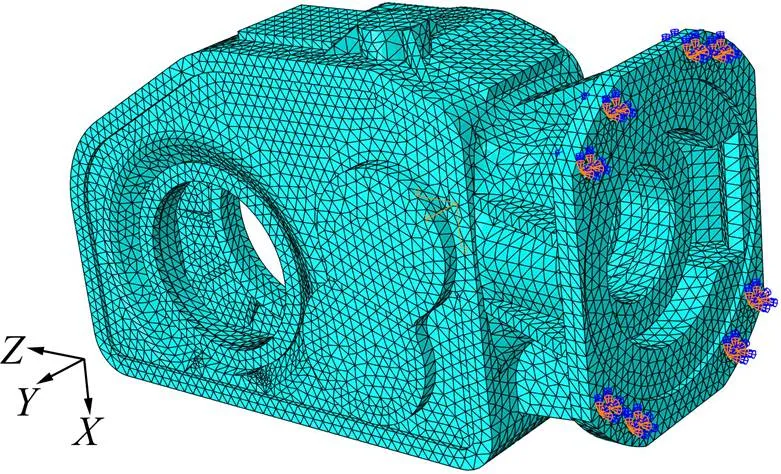
图4 箱体有限元模型

2.2 模态分析

根据100%低地板齿轮箱的实际约束情况，对箱体进行有限元约束模态分析。齿轮箱箱体通过螺栓与转向架连接，因此约束箱体螺栓孔内表面6个自由度，箱体有限元模型如图4所示。在有限元软件中使用Lanczos法进行齿轮箱箱体的约束模态分析，获得箱体的前10阶固有频率及模态振型。表2列出了齿轮箱箱体的前6阶固有频率，箱体前6阶模态振型如图5所示。

箱体前6阶模态振型中，除了第3阶是扭转模态振型，其余的都是摆振模态振型。箱体容易出现振动的位置在输出轴轴承座右侧箱体以及上下侧箱体。箱体前10阶固有频率没有和齿轮箱的啮合频率及其谐波相接近或重合，因此齿轮箱啮合频率不会引起箱体的共振。

表2 箱体固有频率

(a) 1阶振型；(b) 2阶振型；(c) 3阶振型；(d) 4阶振型；(e) 5阶振型；(f) 6阶振型

2.3 动态响应仿真

将齿轮箱刚柔耦合多体动力学分析获得的轴承支反力作为箱体激励，施加在齿轮箱箱体各对应轴承孔耦合点上，如图6所示。在ABAQUS软件中采取直接积分法进行箱体的瞬态动力学仿真，获得了箱体的振动响应。将瞬态动力学仿真获得的箱体振动速度作为齿轮箱直接边界元法辐射噪声分析模型的边界条件。

图6 动态响应模型

3 箱体相似模型设计

3.1 求取π因子

相似模型设计的关键是基于相似理论推导出相似准则[14]，本文采用量纲分析法来导出相似准则。对于齿轮箱的振动问题，其振动特性应当与下列物理参数有关：结构的特征长度，密度，弹性模量，泊松比，振动圆频率，振动位移，速度，加速度，作用力，以及频响函数。取基本物理量单位为质量，长度，以及时间，该系统的无量纲方程如式(1)所示，可用式(2)表示。

上述物理量与基本量的关系可用表3的量纲矩阵表示。

根据因子无量纲的要求，可得到如下的代数方程式：

将长度，密度以及弹性模量作为基本未知量，则上式表示为：

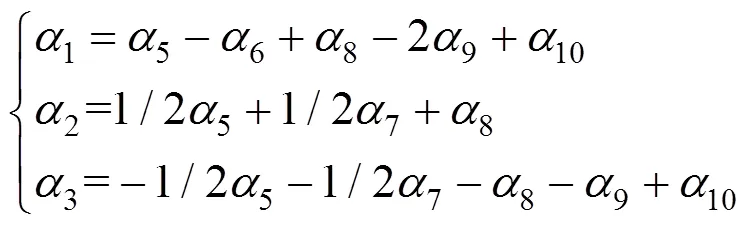
对应的矩阵如表4所示。

表3 量纲矩阵

表4 π矩阵

通过计算可得7个因子：

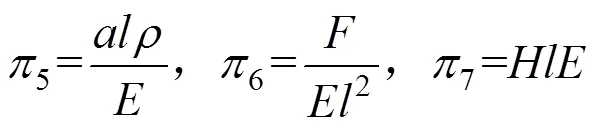
定义为原型与相似模型各物理量的相似比，根据上式可得：

3.2 相似模型制作

要做到试验模型与原模型完全严格相似是很困难的，只能根据所研究的问题，捉住主要影响因素放弃次要影响因素，使模型试验既能尽可能反应所研究问题的真实情况，而又不至太复杂[15−16]。齿轮箱箱体结构复杂且较大，采用传统的方法难以快速且经济的制造出来。随着3D打印技术的发展，复杂结构的快速制造成为了可能。出于经济性的考虑，采用白色树脂材料来进行齿轮箱箱体的制造，其密度为1 300 kg/m³，弹性模量为2 650 MPa，泊松比为0.41。

由于采用了不同的材料制作模型，所以泊松比比尺λ不等于1，无法满足相似条件。然而现有研究表明在对相似模型进行振动特性实验测试时，可以不考虑泊松比的影响，忽略该参数的影响仍然可以取得较高的精度[17−18]。由于相似模型需要进行实验模态分析，在实验过程中需要在箱体表面安装传感器，如果模型寸尺太小，则会使得传感器附加质量对实验测试数据造成较大的误差；如果模型尺寸太大则会造成箱体3D打印制作成本的增加。所以综合考虑各因素，对原型进行1/2等比例的缩小，即几何比尺=2。模型采用与原型相同的边界条件，使用螺栓将相似模型固定在测试台架上。

3.3 模态参数换算

3.3.1 模态振型

设相似模型和原型的某阶振型分别为{}和{}，根据7因子，对于规定的测量点有：

式中：1为几何比尺，为弹性模量比尺，′为一常数，因此{}和{}只差一个常数比值。由于模态振型是各点的振幅比，所以相似模型与原型的同阶模态振型相同。

3.3.2 模态频率

根据前文计算出来的2因子可得：

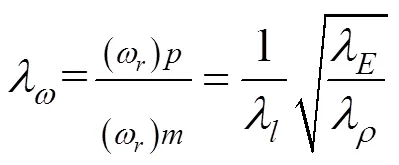
式中：为几何比尺，为弹性模量比尺，为密度比尺。将材料参数代入上式求解可得模态频率比尺为λ=1.87。

4 模态实验

4.1 相似模型实验模态分析

使用丹麦B & K公司生产的B & K PULSE噪声测试系统进行模态实验，模态测试系统由力锤、测试软件、加速度传感器以及数据采集卡4个部分组成，测试系统如图7所示。

图7 模态测试系统

相似模型的结构比较小，布置多个传感器会因为过多的传感器附加质量而对测试结果产生较大的误差。根据测试经验，使用2个加速度传感器进行实验测试。相似模型是树脂材料，不具有磁性，采用磁性贴片将传感器和箱体模型相连接。由于实验难以获得相似模型扭振模态参数，因此只对摆振模态参数进行测量。实验测试如图8所示。经过多次测试，得到的相似模型前六阶模态频率如表5 所示。

图8 模态测试现场

4.2 仿真数据与实验数据对比

将箱体有限元模态分析获得的模态参数与相似模型实验模态分析获得的模态参数进行对比，发现实验模态分析获得的模态参数没有能与有限元模态分析获得的第3阶模态参数相对应。从有限元分析结果知，箱体第3阶模态振型为扭振模态；又由实验只获得了相似模型的摆振模态参数，因此实验获得的结果无法与有限元分析获得的第3阶模态参数相对应。由上文可知箱体与相似模型的模态频率比尺λ为1.87。将仿真得到的频率与相似模型实验得到的频率进行频率比计算，并计算其与模态频率比尺的相对误差，相对误差如表6所示。相对误差全部低于5%，这说明箱体与相似模型具有动力学相似，同时也说明了箱体有限元仿真模型的正确。

表5 实验模态前6阶固有频率

表6 频率比与相对误差

5 齿轮箱辐射噪声预估

5.1 声辐射分析模型建模

在LMS Virtual.Lab软件中使用直接边界元方法进行辐射噪声的求解，要求声学网格是封闭的。所以需要将齿轮箱箱体表面封闭，采用壳单元来对箱体进行封闭；最后将箱体表面提取的声学网格和壳单元网格进行合并，形成一个完整的箱体声学网格。齿轮箱辐射噪声分析模型的边界条件为瞬态动力学仿真得到的箱体表面振动速度。

声学边界元网格划分的过于粗糙会导致计算数据产生较大误差。对于声学边界元模型来说，通常假设在最小波长内有6个单元[19]。考虑软件的计算效率及计算精度，确定声学网格的单元长度为16 mm。声学网格共计单元6 655个，节点6 657个。如图9为齿轮箱的声学网格。进行齿轮箱的辐射噪声预估需要在齿轮箱外部设置一个矩形场点。根据齿轮装置的验收规范−空气传播噪声的实验规 范[20]，设置矩形场点各平面距离齿轮箱大约1 m。同时在矩形场点4个面上各选取了1个声场点。齿轮箱外部声场网格及4个声场点分布如图10所示。

图9 声学网格

图10 外声场网格

5.2 表面声压及场点声压计算

设定空气密度为1.225 kg/m3，声速为340 m/s，参考声压为2×10−5Pa。采用声学直接边界元法求解，可得到齿轮箱表面各个频率下的声压大小和位置分布。图11展示了齿轮箱在频率为310 Hz时的表面声压的有效值及其分布，其声压最大值为120 dB。齿轮箱外声场在310 Hz时的辐射噪声如图12所示，其声压峰值为101 dB。

图11 表面声压

图12 外声场声压

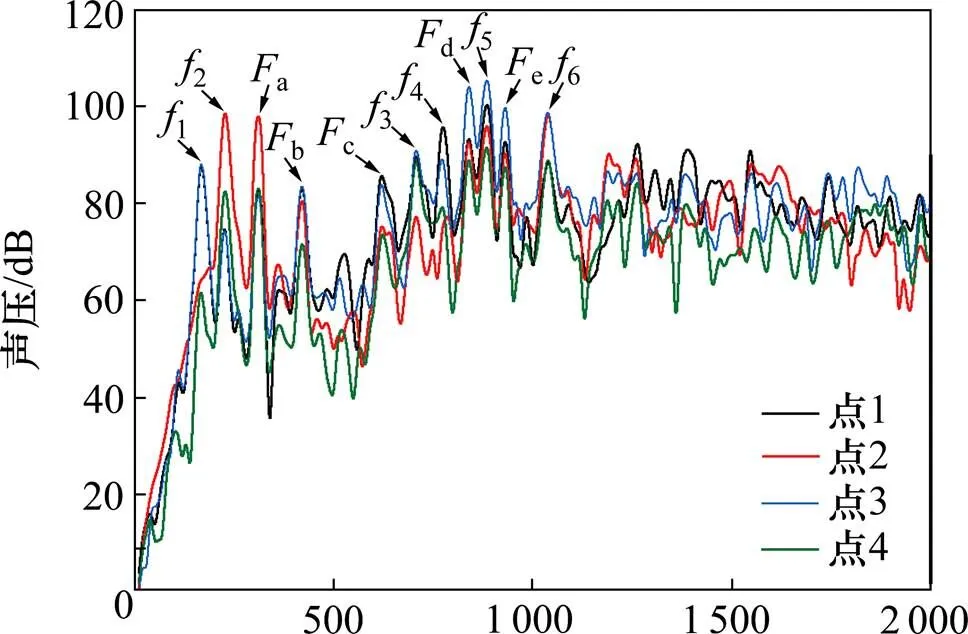
图13 4个声场点噪声值

通过仿真获得了齿轮箱矩形场点中4个声场点的频率噪声曲线。齿轮箱外部声场的声压峰值主要集中在0～2 000 Hz这个频率范围；并且4个声场计算点的噪声值随着频率的变化规律基本一致。图13给出了4个声场点0～2 000 Hz的频率噪声曲线。齿轮箱辐射噪声峰值频率主要集中在啮合频率及其谐波处，如a，b，c，d，e，以及齿轮箱低阶固有频率处，如1，2，3，4，5，6。在齿轮箱前6阶固有频率中，只有第3阶固有频率处没出现明显的辐射噪声峰值，这表明扭振模态对齿轮箱辐射噪声的影响较小。从出现辐射噪声峰值的频率可知，齿轮箱的辐射噪声受啮合频率以及箱体固有频率的影响较大，因此对其的优化设计可以从降低齿轮啮合振动以及箱体的结构优化两方面进行。

6 结论

1) 建立了100%低地板齿轮箱有限元分析模型，对齿轮箱箱体的振动特性进行了分析，表明齿轮副的啮合频率不会激起箱体的共振。

2) 基于相似性理论设计了箱体的相似模型，结合3D打印技术制造了相似模型，并进行了相似模型的实验模态分析，验证了箱体有限元模型的正确性。该方法为大型复杂齿轮箱振动噪声分析的实验验证提供了一种思路，可有效降低实验费用。

3) 建立了100%低地板齿轮箱直接边界元辐射噪声分析模型，预估了齿轮箱表面声压以及齿轮箱外部声场辐射噪声。结果显示齿轮箱辐射噪声频率范围主要集中在0～2 000 Hz，其峰值主要出现在齿轮箱啮合频率及其谐波以及箱体低阶固有频率处。表明对100%低地板齿轮箱的优化设计需要从降低齿轮啮合振动以及箱体结构优化两方面同时进行，同时需要着重关注箱体的低阶摆振模态振型。

[1] Currie G, Burke M. Light rail in australia: Performance and prospects[C]// Australasian Transport Research Forum, Brisbane, 2013.

[2] Vukan R. Vuchic. Comparison of light rail transit with bus semirapid transit[C]// 5th UITP Light Rail Conference, Melbourne, 2000.

[3] 牛悦丞, 李芾, 杨阳, 等. 国外新一代100%低地板有轨电车技术特征及发展趋势[J]. 铁道标准设计, 2018, 62(11): 148−153. NIU Yuecheng, LI Fu, YANG Yang, et al. Technical characteristics and development tendency of new generation foreign 100% low floor tram[J]. Railway Standard Design, 2018, 62(11): 148−153.

[4] Tosun M, Yıldız M, Özkan A. Investigation and refinement of gearbox whine noise[J]. Applied Acoustics, 2018(130): 305−311.

[5] Eade P W, Hardy A E J. Railway vehicle internal noise[J]. Journal of Sound & Vibration, 1977, 51(3): 403−415.

[6] Aherwar A. An investigation on gearbox fault detection using vibration analysis techniques: A review[J]. Australian Journal of Mechanical Engineering, 2011, 10(2): 169−183.

[7] ZHOU Jianxing, S Wenlei, T Qing. Gearbox low-noise design method based on panel acoustic contribution[J]. Mathematical Problems in Engineering, 2014, 2014: 1− 10.

[8] 黄冠华, 张卫华, 梅桂明, 等. 内外激励下高速列车齿轮箱箱体动态响应分析[J]. 机械工程学报, 2015, 51(12): 95−100. HUANG Guanhua, ZHANG Weihua, MEI Guiming, et al. Dynamic response analysis of gearbox housing system subjected to internal and external excitation in high-speed train[J]. Journal of Mechanical Engineering, 2015, 51(12): 95−100.

[9] 林腾蛟, 何泽银, 钟声, 等. 船用齿轮箱多体动力学仿真及声振耦合分析[J]. 湖南大学学报(自然科学版), 2015, 42(2): 22−28. LIN Tengjiao, HE Zeyin, ZHONG Sheng, et al. Multi- body dynamic simulation and vibro-acoustic coupling analysis of marine gearbox[J]. Journal of Hunan University (Natural Sciences), 2015, 42(2): 22−28.

[10] 陆波, 朱才朝, 宋朝省, 等. 大功率船用齿轮箱耦合非线性动态特性分析及噪声预估[J]. 振动与冲击, 2009, 28(4): 76−80. LU Bo, ZHU Caichao, SONG Chaosheng, et al. Coupled nonlinear dynamic characteristics analysis and noise predestination of a large burden marine gearbox[J]. Journal of Vibration and Shock, 2009, 28(4): 76−80.

[11] 任亚峰, 常山, 刘更, 等. 箱体柔性对齿轮传动系统动态特性的影响分析[J]. 振动与冲击, 2017, 36(14): 85− 91. REN Yafeng, CHANG Shan, LIU Geng, et al. Influence of housing flexibility on the dynamic characteristics of gear transmission systems[J]. Journal of Vibration and Shock, 2017, 36(14): 85−91.

[12] Abbes M S, Bouaziz S, Chaari F, et al. An acoustic– structural interaction modelling for the evaluation of a gearbox-radiated noise[J]. International Journal of Mechanical Sciences, 2008, 50(3): 569−577.

[13] 王富民, 李捷, 杨建伟, 等. 地铁齿轮箱箱体模态及谐响应分析[J]. 机械传动, 2015(9): 146−150. WANG Fuming, LI Jie, YANG Jianwei, et al. Modal and harmonic response analysis of subway gearbox housing[J]. Journal of Mechanical Transmission, 2015(9): 146−150.

[14] C Yuxi, G Shen, H Wang. Maglev vehicle-guideway coupling vibration test rig based on the similarity theory[J]. Journal of Vibration and Control, 2016, 22(1): 286−295.

[15] Z Zerong, W Yongyan, F Zhimin. Similarity analysis between scale model and prototype of large vibrating screen[J]. Shock and Vibration, 2015, 2015: 1−7.

[16] Moschoudis A P, Tsekouras G J, Kanellos F D. Design of particular electrical machines by using similarity theory and scale factors[C]// 2014 International Conference on Electrical Machines (ICEM). IEEE, 2014.

[17] 林皋, 朱彤, 林蓓. 结构动力模型试验的相似技巧[J]. 大连理工大学学报, 2000, 40(1): 4−11. LIN Gao, ZHU Tong, LIN Bei. Similar techniques for structural dynamic model tests[J]. Journal of Dalian University of Technology, 2000, 40(1): 4−11.

[18] 朱彤. 结构动力模型相似问题及结构动力试验技术研究[D]. 大连: 大连理工大学建设工程学部, 2004: 67− 75. ZHU Tong. Research on structural dynamic model similarity problems and structural dynamic test technology[D]. Dalian: Dalian University of Technology, Department of Construction Engineering, 2004: 67−75.

[19] 李增刚, 詹福良. Virtual. Lab Acoustics声学仿真计算高级应用实例[M]. 北京: 国防工业出版社, 2010: 46− 48. LI Zenggang, ZHAN Fuliang. Virtual. Lab Acoustics advanced application example of acoustic simulation[M]. Beijing: National Defense Industry Press, 2010: 46−48.

[20] 中国标准出版社第二室. 环境监测方法标准汇编. 噪声与振动[S]. The second room Standard Press of China. Compilation of standards for environmental monitoring methods. Noise and vibration[S].

Vibration analysis and noise prediction of 100% low floor gearbox

PENG Ruitao, XIE Yanpei, LUO Xiuqiang, HU Congfang, LIU Xianghuan

(School of Mechanical Engineering, Xiangtan University, Xiangtan 411105, China)

Vibration analysis and noise prediction of 100% low floor gearbox can provide a basis for its design and optimization. A rigid-flexible coupling multi-body dynamics model of 100% low floor gearbox coupled with transmission system and structural system was established, and the bearing reaction force was calculated. The gearbox modal analysis model was established and the vibration characteristics of the housing were studied. A similar model of the housing was designed based on the similarity theory, and an experimental modal analysis was performed to verify the correctness of the finite element model. The bearing reaction force obtained by the rigid-flexible coupled multi-body dynamics simulation was used as the excitation of the housing, and the direct integration method was used to calculate the vibration response of the housing. Then, using the housing vibration velocity as the boundary condition, the direct boundary element method radiation noise analysis model of the gearbox was established, and the sound pressure on the surface of the gearbox and the external sound field radiation noise were predicted. The results show that the noise peak frequency of the gearbox radiated noise frequency domain curve appear at the meshing frequency of the gear pair and its harmonics, as well as the low- order natural frequency of the housing.

100% low floor; gearbox; rigid-flexible coupling dynamics; vibration characteristics; similarity theory; radiated noise

TB532

A

1672 − 7029(2020)12 − 3181 − 09

10.19713/j.cnki.43−1423/u.T20200128

2020−02−21

国家自然科学基金资助项目(51975504，51705442)；湖南省自然科学(株洲)联合基金资助项目(2018JJ4082)；湖南省教育厅优秀青年项目(19B539)

彭锐涛(1982−)，男，湖南衡阳人，教授，从事高效精密加工与传动研究；E−mail：pengruitao@xtu. edu.cn

(编辑 阳丽霞)