冲击荷载作用下粗粒土破碎过程演化研究

王启云，林华明，张丙强，项玉龙，臧万军

冲击荷载作用下粗粒土破碎过程演化研究

王启云，林华明，张丙强，项玉龙，臧万军

(福建工程学院 土木工程学院，福建 福州 350118)

冲击荷载作用容易导致粗粒土颗粒破碎，从而影响其工程特性。为探索冲击荷载作用下粗粒土的颗粒破碎特性及粒度分布演化规律，采用YX-30型电动重型击实仪对2组典型级配的粗粒土开展冲击试验，探讨含水量、冲击次数及级配对粒组变化的影响。为进一步描述颗粒破碎演化中间过程，在颗粒含量与相对粒径坐标系中提出一种连续级配粗粒土的级配方程，并验证该方程的适用性。在相对坐标系中定义一个破碎率指标，推导破碎率指标的数学表达式，利用破碎率指标研究冲击荷载作用下粗粒土颗粒破碎演化规律。研究结果表明：本文提出的破碎率指标可以描述粗粒土颗粒破碎演化中间过程，颗粒破碎率随含水量的增加呈先增大后减小的趋势，颗粒破碎率与冲击能的关系可采用双曲线函数来描述。

粗粒土；颗粒破碎；冲击荷载；级配演化

1 冲击试验

1.1 试验设备

试验采用的设备为YX-30型粗粒土电动重型击实仪，筒直径为30 cm，高度为28.8 cm，体积为20 357 cm3，允许最大装样粒径为60 mm。冲击锤重为35.2 kg，击锤下落高度为60 cm，直径为15 cm。

1.2 试验材料与方法

采用不同粒径的碎石与黏土进行混合，制备了2组符合路基填料要求的典型连续级配的粗粒土，级配曲线见图1。碎石为弱风化粉砂岩，棱角分明，粒径范围2～40 mm。

图1 试样级配曲线

级配1土样设计含水量为2%，6%，8%，10%，12%和14% 6个等级，级配2土样设计含水量为6%，8%，10%，12%和14% 5个等级，制样后闷料24 h，再进行冲击试验。试样分3层冲击，每层88击，单位体积冲击能为268.4 kJ/m3。为研究冲击能对粗粒土颗粒破碎的影响，对级配2开展不同次数的冲击试验，在最优含水量处每层土样冲击次数分别取10次，44次，88次，132次和176次，对应的单位体积冲击能分别为30.5，134.2，268.4，402.6和536.8 kJ/m3。

1.3 冲击试验结果

粗粒土干密度与含水量关系曲线如图2 所示。可以看出，级配1和级配2土样的最优含水量分别在10%，6%左右，级配2的最大干密度大于级配1。粗粒土级配组成一定时，含水率与干密度关系近似呈抛物线形，且含水量低时干密度随含水量的增大而增大，当含水量增至某值时，干密度随含水量的增大反而减小。

图2 粗粒土干密度与含水量关系曲线

在不同冲击能作用下，级配2土样的干密度与冲击能的关系曲线如图3所示。

图3 粗粒土干密度与冲击能关系曲线

从图3可以看出，当冲击能小于268.4 kJ/m3，干密度随着冲击能的增加而增大，当冲击能大于268.4 kJ/m3，干密度随着冲击能的增加趋于一定值或出现减小的现象。这说明冲击荷载存在一个最佳冲击能，使得粗粒土可达到最大干密度值。本次试验最佳冲击能均为268.4 kJ/m3，相应的冲击次数为88击/层。

2 颗粒破碎特征与机理分析

为获得冲击荷载作用下粗粒土填料的颗粒破碎特性，同时避免取样造成的误差，对整个试样进行筛分，本次实验每个试样的总重量约40 kg。冲击荷载作用下，颗粒含量的变化量如图4～6所示。

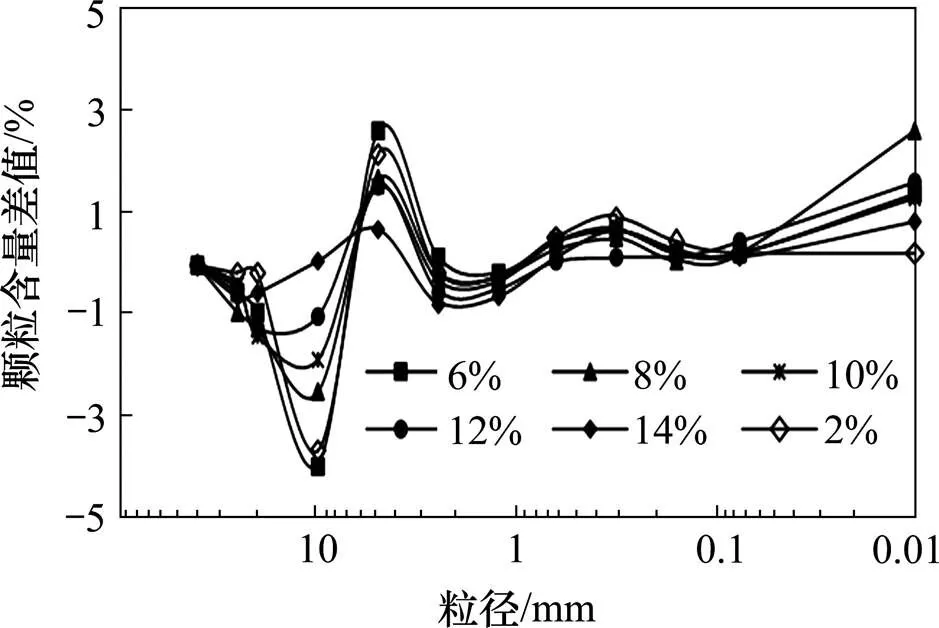
图4 级配1颗粒含量变化曲线

图5 级配2颗粒含量变化曲线

从图4可以看出，级配1土样中1.25～5 mm，20～40 mm粒组的含量减少，当含水量低于8%时，10～20 mm的颗粒减少超过2.5%，增加的粒组主要集中在5～10 mm和1.25 mm以下颗粒，其中5～10 mm粒组颗粒、0.075 mm以下的颗粒平均增加1%以上。分析表明，在冲击荷载作用下，级配1土样的破碎方式以破裂、破碎为主，研磨为辅。从图5可以看出，级配2中2.5～10 mm，25～40 mm粒组的含量减少，尤其是2.5～5 mm的颗粒减少超过4%，增加的粒组主要集中在1.25 mm以下，平均增加在9.18%，其中0.315～0.63 mm粒组颗粒、0.075 mm以下的颗粒均增加2%以上，其中0.63～1.25 mm，0.16～0.315 mm粒组增加1%以上。分析表明，在冲击作用下级配2的破碎方式以破碎、研磨为主，破裂为辅。

图6 级配2不同击实次数后颗粒含量变化

由图6可知，不同的冲击能作用下，当冲击次数大于88次时，级配2土样的1.25 mm以上粒组均存在减少，其中2.5～10 mm粒组含量减少超过4%，25～40 mm粒组含量减少超过2%，当击实次数少于88次时，级配2土样中10～20 mm粒组略有增加。从图6还可以看出，无论冲击能大小，1.25 mm以下的颗粒含量均显著增加，5个击实试样平均增加10.82%，其中0.075～0.16 mm，0.16～0.315 mm，0.63～1.25 mm粒组含量增加在1%～2%，0.315～0.63 mm粒组含量平均增加2.78%，0.075 mm以下粒组含量平均增加达3.7%。

对比图4～6发现，级配相同的粗粒土颗粒破碎具有相似性，即不同含水量、不同冲击次数，颗粒破碎的粒组的变化基本一致，这说明粒径分布对粗粒土的颗粒破碎方式影响大，含水量对颗粒破碎方式影响相对较小。从粒组的变化曲线还可以看出，某粒组颗粒破碎后将导致该组粒径的下一级粒组含量和0.075 mm以下的粒组含量增加，颗粒破碎具有连续性。

为进一步分析冲击荷载作用下粒组的变化情况，将每个击实试样颗粒含量的增加部分或减小部分的粒组含量部分累加，可到级配1土样和级配2土样的粒组变化情况如图7～8所示。

(a) 级配1；(b) 级配2

图8 级配2颗粒增/减量与冲击次数关系曲线

从图7中可以看出，级配2土样的颗粒破碎增量大于级配1土样的颗粒破碎增量，级配2的颗粒破碎程度较高，表明粗粒土颗粒破碎与级配关系非常密切。随着试样含水量的增加，级配1和级配2的土样颗粒破碎增量呈现先增大后减小的趋势，级配1和级配2土样颗粒破碎达到最大程度时，对应含水量分别为6%，4%时，低于最优含水量10%，6%。当粗粒土含水量低于某一数值时，随着含水量的增加，颗粒之间变得润滑，从而引起摩阻力减小，有效接触压力增大，冲击能转化为土体的弹性变形能、颗粒间的摩擦耗能、颗粒破碎耗能，颗粒出现摩擦和翻转，且破碎程度逐渐增大，粗粒土逐渐趋于密实。当粗粒土中含水量高于某一数值时，随着含水量的增加，颗粒间逐渐充满孔隙水，摩阻力进一步减小，部分冲击能被孔隙水耗散，冲击能转化为土体的弹性变形能、颗粒间的摩擦耗能、颗粒破碎耗能的三者总量逐渐减小，颗粒破碎效应逐步降低，但粗颗粒会持续滑动、翻转，细颗粒逐步迁移至粗颗粒形成的孔隙中，并在最优含水量时试样达到最为密实的状态。当粗粒土中的含水量高于最优含水量时，冲击能被孔隙水耗散逐渐增大，颗粒破碎耗能持续降低，颗粒破碎程度逐步减小，粗颗粒翻转、细颗粒迁移程度逐步降低，试样的密实度也就随之减小。

从图8中可以看出，粗粒土颗粒破碎总量和各粒组的增量均随着击实次数的增加而增大，但增加的速率逐渐变慢。

从图8还可以看出，在不同冲击能的作用下，级配2土样增加的粒组主要集中在1.25 mm以下，其中0.075 mm以下的颗粒占总颗粒增量约1/3。当击实次数小于88次时，冲击能有效转化为土体的弹性变形能、颗粒间的摩擦耗能、颗粒破碎耗能，颗粒破碎程度逐渐增大，粗颗粒会出现滑动、翻转，细颗粒出现迁移现象，颗粒相对位置改变，并逐渐趋于密实，颗粒在击实88次时，颗粒排列达到最优状态，此时密实度达到最大值。当击实次数不断增加，冲击能仍转化为土体的弹性变形能、颗粒间的摩擦耗能、颗粒破碎耗能，但由于颗粒排列在88次时已经达到最优状态，土骨架结构由土体相互咬合作用逐渐转变为依靠土体颗粒间滑动摩擦力作用，粗颗粒破裂效应减小，研磨效应增加，从而导致0.075 mm以下的颗粒含量明显增加，粗颗粒受到挤压作用而出现翻转，土体密实度降低。

3 级配方程及适用性验证

研究粗粒土颗粒破碎演化首先需要解决级配的准确表述问题，若能找到准确描述级配的数学描述，颗粒破碎定量表述就较容易实现[10]。迄今为止，级配的准确定量描述仍依赖于级配曲线。

自分形理论应用于岩土体以来，学者提出许多岩土体颗粒或孔隙的分形模型[10]。基于分形理论，Talbot提出的级配方程[16]可表示为：

式中：为粒径为的颗粒的通过质量百分率；max为最大粒径；为分形维数。为方便分析，做归一化处理，定义相对粒径变量，建立相对坐标系。

则式(1)可转化为：

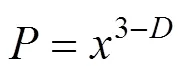
对式(3)两边取对数：

式中：为线性回归求得直线部分的斜率。

式(4)表明在双对数坐标系中，小于某粒径的土粒累计百分比含量与相对粒径为线性关系。

粗粒土的典型连续级配形态曲线[15]常表现为双曲线形、形或直线形，其典型粒径累积曲线如图9所示。采用式(4)对图9中数据进行分析，结果见表1。可以看出，双曲线型级配曲线采用线性函数进行拟合相关系数2大于0.95，但反型、直线型曲线采用线性函数进行拟合相关系数2相对较低，说明式(1)适应性不够强，表述显然过于简单。

通过对大量连续级配粗粒土的双自然对数坐标系中级配曲线进行统计分析，发现粒径含量百分比与相对粒径采用二次函数来表示是可行的，构造如下关系式：

式中：¢=ln，¢=ln，，为参数。

为保证式(5)函数变量′在(lnmin/max，0)区间范围内曲线呈单调递增函数，对式(5)进行微分求导，有：

根据级配曲线确定的参数，应满足：

采用式(5)对图9中曲线进行拟合，拟合参数如表1所示。

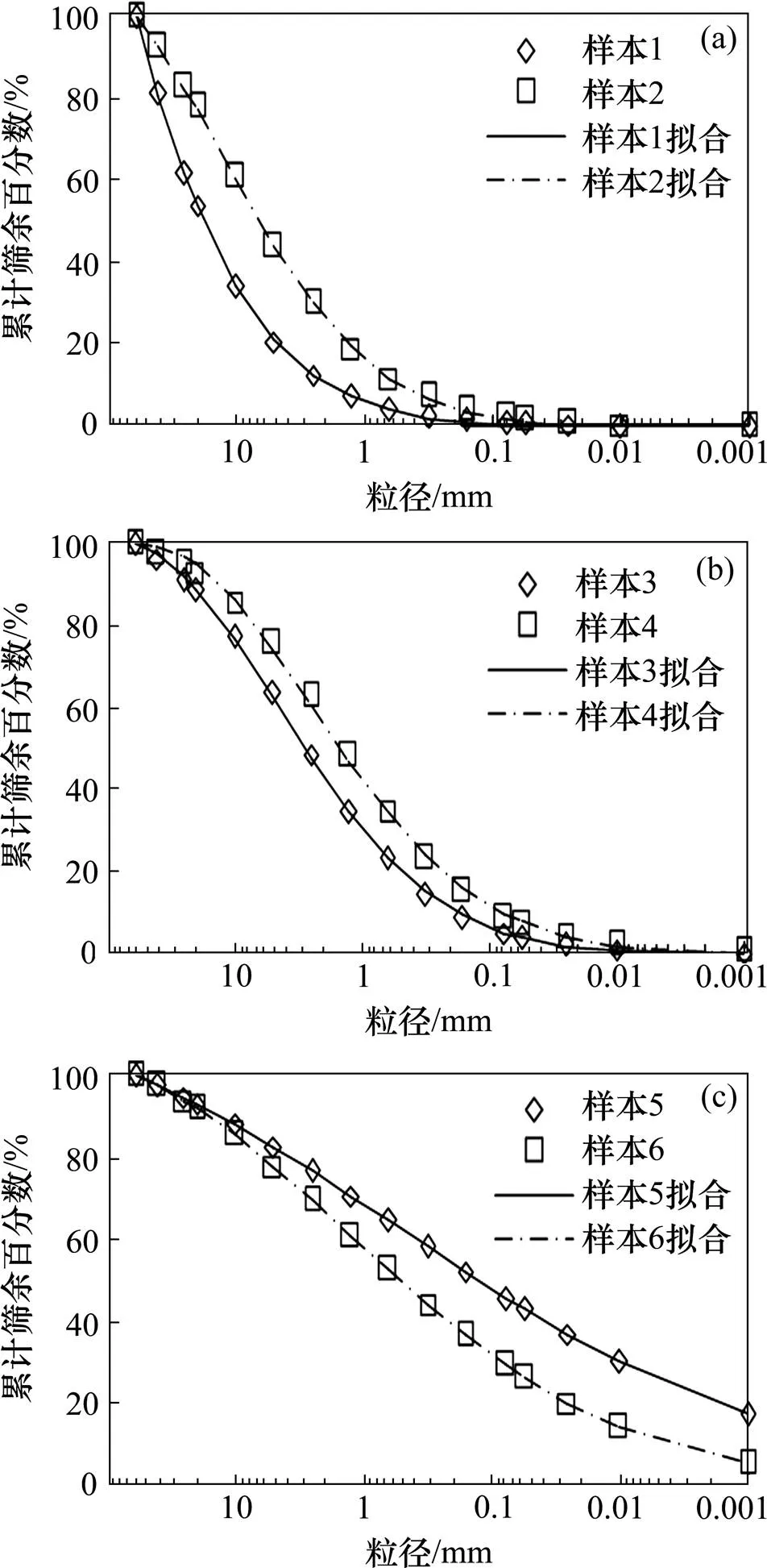
(a) 双曲线型；(b) 反S型；(c) 直线型

表1 非线性拟合参数

表1说明二次函数对双曲线形、形或直线形等3种曲线形态的¢−¢具有良好的适应性。

对二次函数(5)求解，可得到粗粒土级配曲线方程表达式，可用式(8)或式(9)表示：

根据表1中数据和公式(9)，获得级配曲线如图9所示，可以看出，本文提出的级配方程式(9)对不同形态级配的粗粒土具有良好的适用性。

4 基于级配方程的破碎率

在众多的描述颗粒破碎的破碎率指标中，B和B使用最为广泛，两者均存在明显的不足[15]。但B和B提供一种定义破碎指标的思路，即可以采用相同量纲的比值作为破碎率指标。

式中：S0和S1分别为初始级配曲线、试验后级配曲线与相对粒径坐标所围成的面积，如图10所示。

式(10)在计算结果为0到无穷大，能够反映级配整体的变化情况，数值越大表明级配曲线变化越大，颗粒破碎越明显。

由于粒径的最小值不能为0，因此积分求解时需设定值的下限d。现有研究表明粗粒土的工程特性主要取决于粗粒含量及细料的性质[17]。因此，本文参考Hardin提出的积分曲线限值，取d=0.074 mm。显然，当级配曲线中最小粒大于0.075 mm时，d直接取最小粒径。由级配曲线与=max=1和=0.074/max所围成的面积可表示为：

式中：d为对应的相对粒径的筛分通过率微分 形式。

由于式(11)无法获得精确数值解，可采用自适应Lobatto数值积分方法求解。

由于级配曲线是由筛分实验确定，而级配方程是由级配曲线回归分析得到，这将导致式(12)计算结果存在误差。

表2 级配方程计算误差分析

5 粗粒土颗粒破碎演化分析

利用式(8)或式(9)对击实后的级配曲线进行参数反演，获得识别的模型参数，，如表3～5 所示。

表3 级配1识别的模型参数值

从表3～5看出，级配方程能较好地描述冲击荷载试验后粗粒土的级配情况。根据破碎率指标式(12)，计算获得击实荷载作用下粗粒土颗粒破碎率与含水量关系曲线如图11所示，破碎率与冲击能关系曲线如图12所示。

表4 级配2识别的模型参数值

表5 不同冲击能级配2识别的模型参数值

图11 颗粒破碎率与含水量关系

从图11可以看出，颗粒破碎率指标随着含水量的增加总体呈先增加后减小的趋势，颗粒破碎率指标计算值与实验值较为吻合，最大误差约为0.5%。对比图11和图7，可以发现粗粒土颗粒破碎率与含水量关系曲线、颗粒破碎总量与含水量关系曲线形态总体来说较为一致，进一步证明了基于级配方程的颗粒破碎方程的合理性，该方程可用来描述颗粒破碎的中间过程。对比图11和图2中数据，可以发现粗粒土颗粒破碎率总体上随干密度增加而增大，且破碎率最大值对应的试样干密度低于最大干密度。

图12 级配2颗粒破碎率与冲击能关系

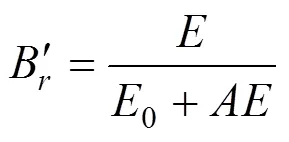
式中：，0为拟合参数。

6 结论

1) 冲击荷载作用下，粗粒土颗粒含量的变化量随含水量呈现先增加后减小的趋势，颗粒含量的变化量随冲击能的增加而增大，颗粒破碎与级配关系密切，细粒含量较少的粗颗粒土在击实荷载作用下颗粒破碎以破裂、破碎为主，细粒含量较多的粗颗粒土在冲击荷载作用下颗粒破碎以破碎、研磨 为主。

2) 在颗粒含量与相对粒径坐标系中，提出了适用于连续级配粗粒土的级配方程，并对方程的适用性进行论证，该方程可以描述反型、双曲线、直线等3种典型级配曲线形态，该方程将有助于定量研究土体力学性质与颗粒级配之间关系问题。

[1] XIAO Y, LIU H L, CHEN Q S, et al. Evolution of particle breakage and volumetric deformation of binary granular soils under impact load[J]. Granular Matter, 2017, 19(4): 1−10.

[2] 丁建源, 陈晓斌, 张家生, 等. 基于对数几率回归模型的粗颗粒土颗粒破碎过程演化研究[J]. 岩土力学, 2019, 40(4): 1465−1473. DING Jianyuan, CHEN Xiaobin, ZHANG Jiasheng, et al. Predicting model for coarse-grained soil particle breakage process using logarithmic probability regression mathematic method[J]. Rock and Soil Mechanics, 2019, 40(4): 1465−1473.

[3] Lade P V, Yamamljro J. Significance of particle crushing in granular materials[J]. Journal of Geotechnical Engineering, 1996, 122(4): 309−316.

[4] Marsal R J. Large scale testing of rock fill materials[J]. Journal of the Soil Mechanics and Foundations Division, American Society of Civil Engineering, 1967, 93(2): 27−43.

[5] Hardin B O. Crushing of soil particles[J]. Journal of Geotechnical Engineering, 1985, 111(10): 1177−1192.

[6] Einav I. Breakage mechanics-Part I: Theory[J]. Journal of the Mechanics and Physics of Solids, 2007, 55(6): 1274− 1297.

[7] 韩华强, 陈生水, 傅华, 等. 循环荷载作用下堆石料的颗粒破碎特性[J]. 岩土工程学报, 2017, 39(10): 1753− 1760. HAN Huaqiang, CHEN Shengshui, FU Hua, et al. Particle breakage of rockfill materials under cyclic loadings[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(10): 1753−1760.

[8] Salim W, Indraratna B. A new elastoplastic constitutive model for coarse granular aggregates incorporating particle breakage[J]. Canadian Geotechnical Journal, 2004, 41(4): 657−671.

[9] 郭万里, 朱俊高, 钱彬, 等. 粗粒土的颗粒破碎演化模型及其试验验证[J]. 岩土力学, 2019, 40(3): 1023− 1029. GUO Wanli, ZHU Jungao, QIAN Bin, et al. Particle breakage evolution model of coarse-grained soil and its experimental verification[J]. Rock and Soil Mechanics, 2019, 40(3): 1023−1029.

[10] 陈镠芬, 高庄平, 朱俊高, 等. 粗粒土级配及颗粒破碎分形特性[J]. 中南大学学报(自然科学版), 2015, 46(9): 3446−3453. CHEN Liufen, GAO Zhuangping, ZHU Jungao, et al. Gradation of coarse grained soil and fractal geometry character of particle breakage[J]. Journal of Central South University (Science and Technology), 2015, 46(9): 3446− 3453.

[11] Mcdowell G R. On the yielding and plastic compression of sand[J]. Soils and Foundations, 2002, 42(1): 139−145.

[12] Ozkan G, Ortoleva P J. Evolution of the gouge particlesize distribution: A Markov model[J]. Pure and Applied Geophysics, 2000, 157(3): 449−468.

[13] Coop M R, Sorensen K K, Freitas T B, et al. Particle breakage during shearing of a carbonate sand[J]. Géotechnique, 2004, 54(3): 157−163.

[14] 蔡正银, 李小梅, 关云飞, 等. 堆石料的颗粒破碎规律研究[J]. 岩土工程学报, 2016, 38(5): 923−929. CAI Zhengyin, LI Xiaomei, GUAN Yunfei, et al. Particle breakage rules of rockfill materials[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(5): 923−929.

[15] 郭万里, 朱俊高, 王青龙, 等. 基于级配方程的粗粒料级配演化预测模型[J]. 中南大学学报(自然科学版), 2018, 49(8): 2076−2082. GUO Wanli, ZHU Jungao, WANG Qinglong, et al. Mathematical model based on the gradation equation for predicting gradation evolution of coarse-grained soils[J]. Journal of Central South University (Science and Technology), 2018, 49(8): 2076−2082.

[16] Talbot A N, Richart F E. The strength of concrete-its relation to the cement aggregates and water[J]. Illinois Univ Eng Exp Sta Bulletin,1923, 137: 1−118.

[17] 陈坚, 罗强, 陈占, 等. 客运专线基床底层砾石土填料物理力学性质试验研究[J]. 铁道学报, 2011, 33(7): 91− 97. CHEN Jian, LUO Qiang, CHEN Zhan, et al. Experimental research on physical and mechanical properties of gravelly soil filling the base course of the subgrade bed of passenger dedicated line[J]. Journal of the China Railway Society, 2011, 33(7): 91−97.

Evolution of particle breakage process of coarse-grained soil under impact load

WANG Qiyun, LIN Huaming, ZHANG Bingqiang, XIANG Yulong, ZANG Wanjun

(College of Civil Engineering, Fujian University of Technology, Fuzhou 350118, China)

The particle breakage of coarse-grained soil occurs under impact load, and it may have a greater impact on its engineering characteristics. In order to investigate the particle breakage and evolutions of particle size distribution of coarse-grained soil under impact load, the impact test was carried out for two groups of typical graded coarse-grained soil by YX-30 electric heavy compaction, and the granulometric composition of moisture content, impact times and gradation were discussed. To further describe the intermediate process of particle breakage evolution, a new gradation equation was put forward in particle contents and relative particle size coordinate system, which could be used to describe continuous gradation of coarse-grained soil, and its adaptability was validated. A new particle breakage index was presented based on relative coordinate system, and then the mathematic expression was presented, the index was used to study the evolution law of particle breakage of coarse-grained soil under impact load. The results show that evolution of particle breakage process of coarse-grained soil under impact load can be described by the index presented in the paper. The particle breakage index increase and then decrease with the increase of moisture content, and the relation between the index and compaction work can be approximated by a hyperbola.

coarse-grained soil; particle breakage; impact load; evolution of grain size distribution

TU432

A

1672 − 7029(2020)12 − 3072 − 09

10.19713/j.cnki.43−1423/u.T20200116

2020−02−17

国家自然科学基金资助项目(51508097)；福建省杰出科研青年人才培育计划项目(GY-Z160147)；福建工程学院科研发展基金资助项目(GY-Z18169，GY-Z18170)；福州市科技局资助项目(2018-G-77)

王启云(1986−)，男，湖南祁阳人，副教授，博士，从事路基动力学方面的研究；E−mail：wangqiyun860519@163.com

(编辑 涂鹏)