基于下肢关节点运动关系的特定人群步态识别
吉林警察学院,吉林 长春130000
人体的行走是全身运动系统协调控制和活动的结果,是一个复杂的综合运动过程。从幼儿到成年经过一定的锻炼就会形成行走运动的动力定型,使行走运动具有了相对稳定的规律性[1],但是由于个体所处的环境有差异,每个人行走姿势又各具特点,构成了行走运动的特殊性,这也使广大科研人员产生了浓厚的兴趣,如何量化人体行走特征,为虚拟现实、医疗诊断、视频识别、人工智能等服务,成为当前多学科交叉融合研究的重要内容[2-4]。
根据提取、运算的特性,本文提出的一种以运动过程中关节点空间距离为参考量的人体运动规律认定方法。此方法丰富了视频侦查的理论基础,为以后相关研究提供了理论支持。
1 人体步行协调性研究
1.1 步态运动分析
步态是人体在日常生活中利用下肢体进行行走、跑步、跳高、骑行、踢踩等下肢体运行姿态的统一称呼[5],其涉及到很多研究领域,但主要关系到人体结构、行为及心理活动、功能运动调节系统等诸多因素,是日常生活中最基本的动作,在其中又分为周期性运动和非周期性运动,其中走路、跑步等为周期性运动,踢球、蹦跳等为非周期运动,周期性运动往往会体现人体长时间运动特点。一个人的正常步态,是指人身体保持健康状态,在自我最放松、最正常、无强迫意识的姿态行进时的步态,其具有明显得周期性、协调和均衡的特点,并且由于步态特征是下肢长时间与地面等客体接触受其制约作用形成的,具有很高的稳定性[6]。
1.2 步态周期特点
步态周期根据不同运动姿势具有不同特点,本文研究主要针对的是正常人自然行走过程中的步态周期研究,通过对于人体下肢自然行走步态的分析,可以确定主要运动周期参数有以下几种:
1.2.1 步态周期 通常根据人的行走过程可以将人体自然行走中以任意一只脚支撑时定义为起始时刻,到该脚第二次形成完整支撑时为终止时刻,开始时刻至终止时刻的整个过程定义为一个周期。
同时该种步态周期可细化分为两个相位过程:支撑相和摆动相,支撑相是以左右脚整个脚掌部与地面接触过程为观察对象,从每支脚足跟着地开始到足尖离地结束为一个过程时间相,一个步态中期中左右脚共同支撑时间相约占步态周期的60%;摆动相即除去支撑相的运动过程,具体体现为从脚掌足尖离地到该脚掌足跟着地的过程约占步态周期的40%。
1.2.2 其他变化特点 髋、膝、踝等各关节屈伸运动特性,如速度、加速度、关节角速度、角加速度等;力学特性,如足底地面反力、关节力矩等;肌肉特性参数,如肌肉力、肌电信号等[7]。
2 步态稳定性评定
2.1 实验对象选取
2.1.1 关节点选取 在步态特征运动运动协调性的基础上,本文确定了以行走中最稳定的特点颈部、重心和行走过程中变化幅度较大的关节点膝关节、踝关节为参考点。文中关节名称用英文首字母代替,如:R 代表重心、Lk 代表左膝、R-Lk 代表重心到左膝距离参数等。
2.1.2 受试者选取 为更好的完成研究。本文通过对吉林省近五年的重大刑事案件中嫌疑人年龄进行分析,确定了受试者年龄范围,并选取龄差±3 的同质人群(身高、体重、习惯相近)为研究对象,利用双目视频采集设备对20 人400 次正常行走周期进行采集,最终汇总了各关节点三维坐标数据。
2.2 受试者步态稳定性评定
在对人体动力学研究可知,健康人体自然行走过程中下肢运动是受腿部肌肉和骨骼共同作用产生的,是一种动力定型过程,并且随着时间积累越来越巩固、越来越自然,人体下肢形成有规律的对称性变化,同时具有较高的稳定性特点。但一旦人体受到健康状况等因素影响,改变原有的动力定型状态就会体现出运动异常,如行走功能障碍、肢体障碍等,在步态行走特征上的反映是破坏了下肢体运动的对称性,因此在验证人体是否处在健康自然的行走过程和对行走功能综合评定时,步态的运动对称性成为评定的重要标准。而在各个领域中对行走对称性指标评定时,经常用时相对称性指数进行评定,该方法是以步态周期的时间相位判断左右侧腿步态的对称性,具体如下:
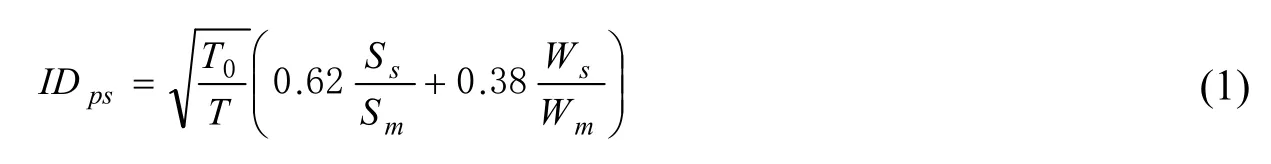
其中:IDps为常数,T0表示人健康、自然情况下的步态周。T为实验对象步态周期。SS、Sm分别表示为实验对象下肢运动时支撑相时左侧、右侧两腿所用最小和最大时间值。Ws、Wm为两腿在摆动相时所占用最小和最大时间值[8]。
这个指标是以模糊数学中隶属函数的定义域为[0,1]的概念为原理,把“1”设定为最健康、自然的步态状态(行走完全对称),把“0”定义为完全丧失下肢行动能力的步态状态,此时健康人在自然情况下的时相对称性在0.95 以上。
但即使是健康人体,在其自然行走过程中难以保证步态的对称性一成不变,并且对称性概念也只是说明了步态周期相位之间的对应关系,并没有完全体现到不同步态特征参数(如步长)在对称性中的作用,无法客观说明人体行走中步态的特点,有时甚至会难以分析出不稳定步态的非对称性。以此为参考,结合Fitts 定律,本文确定了两种检验稳定性的对称性指标作为稳定性研究基础,即:步长对称性指标IDsd,跨步长度执行对称指标IDsp。
由于Fitts 定律是反映运动过程中肢体某点的运动时间与该点距离变化、大小变化的运动精度之间的关系,因此IDsd和IDsp的基本定义为:
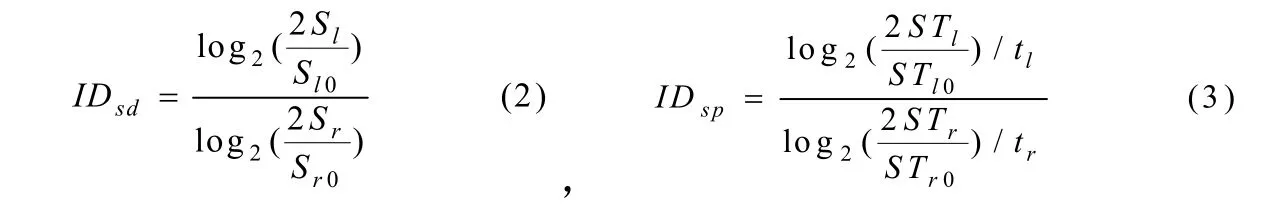
其中:Sl,Sr分别表示为左、右脚跨步的步长;Sl0,Sr0分别为健康人自然步态下两脚跨步的步长精度误差值;STl,STr分别表示为左、右脚跨步的步长;STl0,STr0分别为健康人自然步态下两脚跨步的步长精度误差值。tl,tr分别为两脚跨步执行时间,也就是摆动相所用时间。
同时为反映关节在角度量方面对对称性的贡献,IDsd和IDsp扩展到二维极坐标平面内:

其中:θsl,ρsl,θsr,ρsr表示为两脚的步长在极坐标下的反映;θsl0,ρsl0,θsr0,ρsr0表示为健康人自然行走步态下左右脚的步长精度误差值在极坐标下的反映,公式如下:

其中:θsTl,ρsTl,θsTr,ρsTr分别为左,右脚的跨步长在极坐标下的反映;θsTl0,ρsTl0,θsTr0,ρsTr0分别为健康人自然行走步态下左右两脚的跨步长精度误差值在极坐标下的反映。tl,tr分别为左右脚跨步执行时间,也就是摆动相所占用时间。
步长的对称性指标是主要以反映左右脚行进距离的关系为主,跨步长执行对称性指标反映的主要是左右脚时相之间的关系。
这里极坐标下,IDsdρ和IDspρ除反映下肢执行情况外,也在一定程度上反映路况的因素。
最理想的行走状态是人体处于自然条件下的肢体完全对称运动,在这种对称下步长对称性指标和跨步长执行对称性指标的值均为1。由于个体间存在差异,步长对称性指标和跨步长执行对称性指标的值可能大于1,也有可能小于1。为了利于操作,方便理解,并与时相对称性等其他对称性指标相同,本文将步长对称性指标和跨步长执行对称性指标也设定为[0,1](见公式8~11):
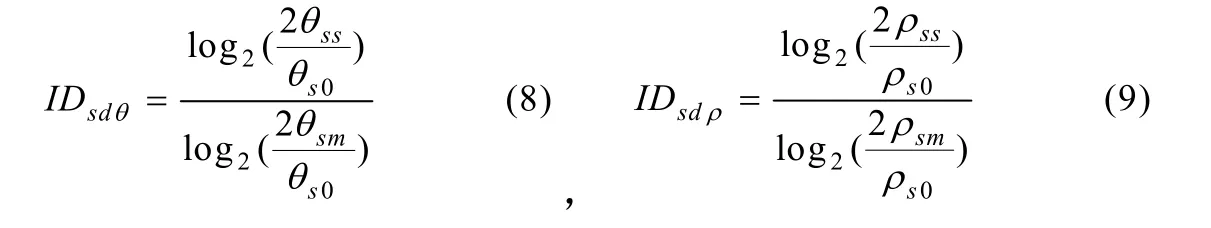
θss和ρss为左右脚步长中较小值;θsm和ρsm为左右脚步长中较大值;θs0和ρs0为健康人自然行走步态下步长的精度误差值。

其中:θSTs,ρSTs和ts分别为值较小侧的跨步长和跨步执行时间;θSTm,ρSTm和tm分别为值较大侧的跨步长和跨步执行时间;θST0,ρST0分别为健康人正常步态下跨步的精度误差值。
利用以上两种指标评定标准,可以有效的对受试者进行行走稳定性研究,对不符合行走稳定性个体数据不进行后续研究。
3 实验及数据分析
通过对受试者行走过程中的综合对称性进行评定可知,受试者步态符合正常行走状态,所采集关节空间数据为稳定步态信息。
3.1 个体步态变化规律研究
本文将视频中各帧中所选四个关节点三维数据(x,y,z)进行汇总,并用欧式距离方法得出每一个步态周期、每一个视频帧中关节点间相互关系参数。然后将每个人一个步态周期内的每个关节间关系视为一个整体进行均值化处理,以其反映数据代表每人一般水平,同时再对每人20 次的周期进行均值化处理,得的10 组见图1(此处以受试者一为例)数据。
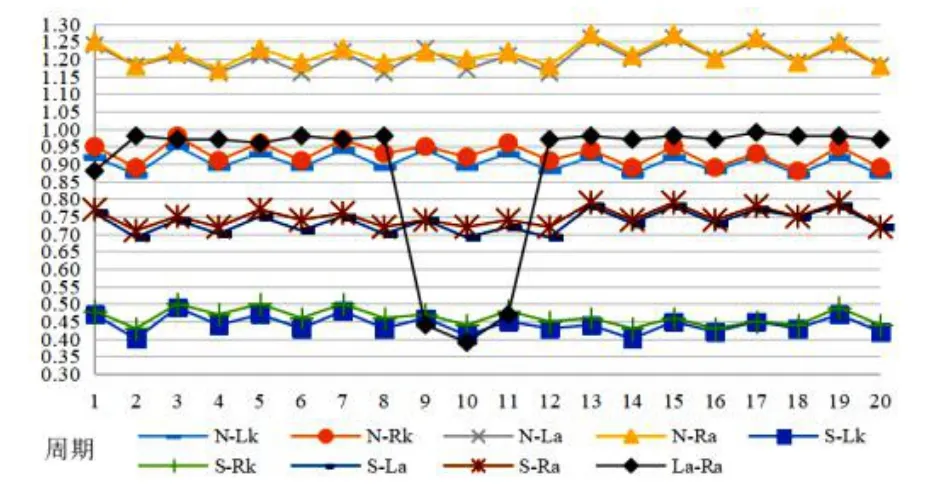
图1 单人每周期内各特征数据散点图Table 1 Scatter points of characteristic data in a cycle of a single person
3.1.1 检验方法 进行分析过程,首先对每名受试者数据中各人特征点距离量的稳定性进行分析,这里选用变异系数(C·V=(SD÷MN)×100%,SD为标准差,MN为平均值)方法来分析人体行走过程中各特征点之间距离变化是否存在稳定性。
同时为了后期对不同人之间特征变化规律比对,我们还对各特征点距离量进行正态性检验,论文选用包含Kolmogorov-Smirnov 大样本(受试者数大于30)正态性检验、Shapiro-Wilk(受试者数小于等于30)小样本正态性检验,我们选取小样本正态性检验,并提出原假设所测数据符合正态分布,当显著值(Sig.)>0.05 说明接受原假设,如果当显著值(Sig.)<0.05 则所测数据拒绝接受原假设。为确保数据分析准确,进一步利用数据的偏度和峰度分析了数据正态性差异。
3.1.2 受试者关节点行位稳定性研究 本文对所有提到9 种特征点相对位置变化规律一一进行了研究,此处以颈部至左膝距离特征为例进行说明。
(1)N-Lk 相对位置变化稳定性研究 通过对受试者的数据提取,得到受试者不同行走周期的N-Lk 数据,共20 组均值数据,首先通过这些数据研究N-Lk 是否存在稳定性,利用SPSS 统计分析软件对N-Lk 所得每个周期均值共计20 数据进行统计学描述所得数据(见表1)。

表1 N-Lk 描述性统计Table 2 N-Lk descriptive statistics
(2)N-Lk 相对位置变化正态性检验 利用SPSS 的正态性检验方法,结合偏度与峰度数据可以综合分析试验受试者特征点相对位置正态性分布情况。通过小受试者Shapiro-Wilk 对自由度(df)为20 的数据进行检验,所得正态性检验显著性水平Sig.=0.067>0.05 表示接受原假设属于正态性分布,即表示其符合正态分布。同时通过偏度数据0.048>0 可知其分布曲线属于右偏分布,与标准对称分布差异较小。通过峰度-1.541<0 可知其分布属于扁平峰分布,与标准正态分布有一定的差异,说明其正态曲线勉强符合正态分布正态性检验(表2)。

表2 Shapiro-Wilk 的N-Lk 正态性检验Table 2 N-Lk normality test on Shapiro-Wilk
正态性检验表明受试者N-Lk 的数据基本符合正态分布,同时通过对其他9 人试验受试者N-Lk,20 组数据正态性检验分析,可发现其中有10 个实验受试者人数据都符合正态分布比例占100%,可靠性较好。
通过以上检验可知N-Lk、N-Rk、N-La、N-Ra、R-La、R-Ra 这些特征量具有较高的稳定性且符合正态分布,而R-Lk、R-Rk、La-Ra 这些特征量稳定性较差。
通过对人体行走过程中特殊关节点相对位置数据进行变异系数法、正态性检验研究后可知:(1)通过对特定特征点与关节点相对位置关系研究可知,同一人的行走过程中行位变化具有稳定性。(2)N-Lk、N-Rk、N-La、N-Ra、R-La、R-Ra这6个关节关系在在人体行走过程中稳定性最好,能够体现个体行走规律,可以利用这些特征点位置关系进行不同人之间差异性比。而R-Lk、R-Rk特征点相互位置关系所反映出的数据稳定性和正态性检验,存在不够稳定和难以满足正态性检验。
4 结语
本文针对视频侦查下犯罪嫌疑人认定需求,提出了基于下肢关节点空间位置关系的步态特征识别方法。利用该方法对高发犯罪年龄段群体对象进行实验研究,实验结果表明N-Lk、N-Rk、N-La、N-Ra、R-La、R-Ra 特征可以进行个体稳定性识别,这是对利关节点特征点进行人体运动特征识别的初步尝试,希望其对下一阶段的深入研究奠定基础,还希望能引导其他人更好更快地推动人体识别、建库的探索与发展。

