理论力学教具DIY系列(二)十字轴万向节及转角差异的演示模型
高云峰
(清华大学航天航空学院,北京100084)
十字轴万向节是一种在工程中应用较为广泛的传动系统,它的主动轴与从动轴可以存在一定的夹角。十字轴万向节具有制造简单、可靠耐用等优势,但存在主动轴与从动轴转速不等的情况。在主动轴旋转 360°的过程中,虽然从动轴也同样旋转 360°,但两者的转角、角速度并不总是相等,这就是十字轴万向节的不等速性。
在理论力学的运动学教学中,十字轴万向节是如何运动的,以及两轴转动的角度关系是一个难点。在实验室中通常将两轴转动的差异用电信号进行转换处理,学生感到不够直观。为了解决这一问题,本文首先设计制作出一个简单的万向节模型,然后导出万向节的转角差异关系,最后设计制作出了一个改进的万向节模型,可以让学生直观地看出两轴转动角度的差异。
1 简化版的万向节设计及制作
十字轴万向轴的要点是:主动轴与从动轴的夹角可以在一定范围内变化,十字轴绕其中心点做定点运动。因此在设计时要考虑这两个因素。
利用 AutoCAD软件进行设计,利用激光切割机对密度板进行加工,可以很快获得十字轴的零部件(图1)。设计中考虑了接口的过盈配合,不需要胶水就可以把框架拼好(图2)。
十字轴的连接轴也用密度板来实现,框架与连接轴之间留有微小缝隙,拼装好后可以灵活转动(图3)。万向节的底板分为两大块,两者可相对做圆周运动且始终保持接触,以方便圆弧边缘有刻度显示主动轴与从动轴的夹角;底板上可以插上立柱,而立柱可与十字轴连接(图4)。

图1 十字轴的零部件

图2 轴的拼装

图3 十字轴的连接
用2根铁轴分别连接十字轴两端的边框,并分别插到底板立柱的孔中,就做好了一个简版的十字轴万向节,它可以实现两轴平行(图5)以及两轴有偏角(图6)时的运动演示,很直观。

图4 可以改变角度的底座

图5 两轴平行情况

图6 两轴有偏角情况
激光切割的精度很高,误差在0.1 mm以内,所以整个装置拼好后,精度还是比较高的。当然以后如果可以用金属来加工,误差可以更小,摩擦也更小,演示效果也会更好。
2 万向节的转动角度关系
结合简易版的万向节模型,可以做运动分析,下面特别关注两轴的转角差异问题。
万向节的运动坐标系如图7所示,所有坐标原点均在O点,但为了方便观看,图中原点放在不同的位置。固定坐标系x0y0z0,初始时刻动坐标系x1y1z1与x0y0z0重合,且主动轴OM固连,OM轴沿x1方向,OA沿y1方向;动坐标系x2y2z2与从动轴ON固连,ON轴沿x2方向,OB沿z2方向;假设OMN始终在x0y0平面内,OM轴与ON轴的夹角为偏角α;OM轴转动φ1后A到了A′,动坐标系变为x3y3z3;ON轴转动φ2后B到B′,动坐标系变为x4y4z4。

图7 万向节的运动分析
在这种假设条件下,A01是单位矩阵,其余各坐标系之间的方向余弦矩阵为

设rA′表示从O到A′的矢量,而表示rA′在坐标系xiyizi中的列阵,根据矢量的列阵在不同坐标系之间的转换关系,则有

因为OA′垂直于OB′,有rA′·rB′=0,或,代入式(1)和式(2)后有

从而得到

由此可见万向节两轴的转动角度是不同的,设Δφ=φ2-φ1,式(3)可以变化为
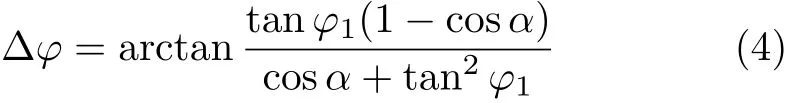
图 8显示了不同偏角情况下两轴转角的差异。偏角α越大,两轴转角的差异就越大。

图8 不同偏角时两轴差异的关系
进一步对式(3)两边求导,可以得到

即两轴角速度之比也随时间周期性变化。
通常在理论力学求解万向节角速度的习题中,会有意识地让φ1=0或φ1=π/2,就是为了避免复杂的运动学分析,但这也容易让学生误解,以为两轴角速度之比是常数。
3 改进版的万向节的设计及制作
为了直观看出万向节两轴转角的差异,可以巧妙利用锥齿轮,把两个非平行的转轴变为两个平行的转轴,再类似钟表的处理方式,把两个平行轴变为共轴的“分针”和“秒针”转动,这样就可以通过“分针”和“秒针”的夹角,直接看出两轴转角的差异。
具体设计中的要点是:在装置示意的俯视图(图 9)和正视图 (图 10)中,齿轮C通过锥齿轮与OM轴连接,然后与齿轮D1连接;齿轮E通过锥齿轮与ON轴连接,然后与齿轮D2连接。而齿轮D1和D2共轴且轴的延长线过O点。

图9 齿轮的位置安排(俯视图)

图10 齿轮连接关系(正视图)
这样的设计保证了当ON轴和OM轴保持不同的偏角α时,齿轮E总可以与齿轮D2啮合。共轴设计将OM和ON的转角同时在齿轮D1和D2中反映出来,再将指针分别与D1和D2齿轮固接,就可以通过看两指针夹角的变化,直观地看出万向节两轴转角的差异。
图11和图12是改进后的装置,其中C,D,E齿轮的齿数还可以适当改变,目的是将两轴转动的差异进行放大。

图11 把水平轴变为竖直轴

图12 变为共轴运动

