大型飞机操纵面极限环颤振特性研究1)
吕继航 罗琳胤
*(中航通飞研究院研发中心,广东珠海519040)
†(中航通飞研究院科学技术委员会,广东珠海519040)
飞机操纵面是飞行过程中最易发生颤振的部位。对于飞机操纵系统,结构非线性是不可避免的,因此操纵面具有更加复杂的颤振型态和影响因素,常会导致操纵面产生复杂的运动现象,影响飞机的飞行品质和飞行安全[1]。
为了保证飞行安全,在飞机设计过程中,通常会对操纵面自由间隙进行严格控制,如 MIL-A-8870C,A.P.970,GJB 67.7A-2008等国内外设计规范,均对飞机操纵面的自由间隙做出了规定。但是,按照规范要求进行操纵面自由间隙控制,往往会带来较高的制造成本和维护费用。而且,相对于小型飞机,大型飞机在设计制造和使用过程中,由于结构尺寸大,操纵线系多,连接复杂,以及工艺限制、装配误差及运动磨损等,操纵面自由间隙往往很难满足规范要求,国内外多个型号飞机均出现过操纵面自由间隙不满足规范要求的情况。同时,大型飞机飞行速度更高,通常按颤振要求进行设计,这也容易加剧系统非线性,进而产生各种不利影响。
为了评估操纵面自由间隙引起的颤振不稳定现象,国内外学者开展了大量的研究工作,但大多数研究都局限于自由度较少的简单结构系统,如二元翼型等,偏重于各种非线性分析方法及复杂的分岔、混沌等非线性效应的理论研究,对工程实际中的复杂结构关注不多[2-5]。近年来,已有学者根据工程需要,开始进行含操纵面运动副间隙的三维飞机结构非线性气动弹性研究,并取得了部分成果[6]。
本文根据大型飞机的设计需要,结合设计分析时的工程模型,考虑操纵面的旋转自由间隙特性,采用最小状态拟合技术对偶极子格网法计算得到的非定常气动力进行有理函数拟合,求解操纵面在结构非线性效应下的响应特性,研究操纵面的极限环颤振行为及其影响因素,以期为型号设计提供支持。
1 基本理论
操纵面的自由间隙主要表现为中心间隙特性[7],在没有初始载荷的情况下,其铰链处的间隙特性通常如图1所示。当操纵系统存在中心间隙时,若操纵面偏转角在间隙范围内,则操纵面绕铰链轴的支持刚度为零,此时操纵面处于自由偏转状态;若操纵面偏转角大于间隙值,则操纵系统为操纵面提供线性支持刚度。一般地,这种非线性刚度用分段函数描述
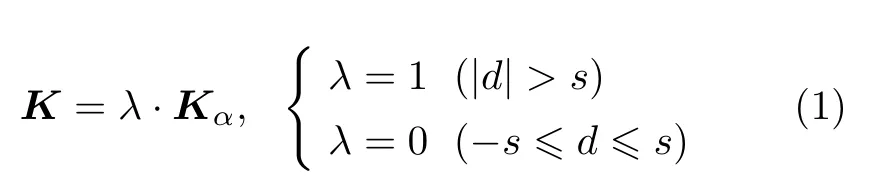
式中,Kα为操纵面偏转自由度对应的线性操纵刚度,d为运动位移,s为间隙值。对于中心间隙,其范围定义为 [-s,s]。
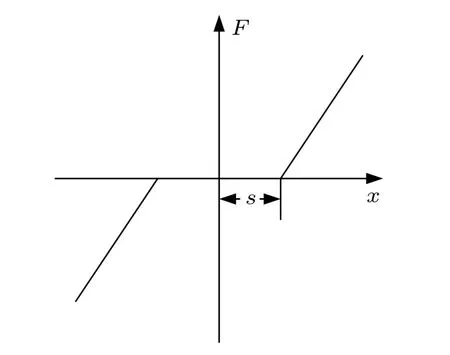
图1 中心间隙非线性
同时,在非线性刚度影响下,操纵面还会产生非线性的弹性恢复载荷,可表示为

式中,αc为操纵面角位移,δs为s对应的角度值。
飞机升力面通常由安定面、操纵面组成,在气动力作用下这两部分都会发生结构变形。因此,非线性刚度计算时,将操纵面角位移定义为

式中,α1为安定面主梁偏转角,α2为操纵面铰链轴偏转角。
根据拉格朗日方程,对于存在操纵面中心间隙非线性环节的系统,用模态坐标表示的气动弹性运动方程可表示为

式中,M为广义质量,C为广义阻尼,K为广义刚度,ξ为广义向量,QA为广义非定常气动力,MR为广义弹性恢复载荷。对于MR,其与操纵面偏转自由度对应的元素为Mr,其余自由度元素均为0。
为了便于求解,将式(4)化为一阶微分方程
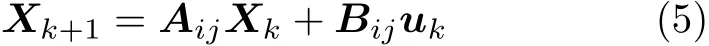
式中,X为状态变量,k为时间步,A和B分别为时域空间的系数矩阵,u为外部扰动向量。
对于式(5),给定初始扰动,采用数值积分方法按照等时间步长进行推进求解,即可得到气动弹性系统在操纵面自由间隙影响下的非线性响应特性。
当然,利用模态法得到的都是广义坐标下的参数结果,可将广义坐标转化为物理坐标

式中,χ为物理向量,Φ为模态振型矩阵。
2 非定常气动力计算方法
非定常气动力计算是气动弹性求解中的重要部分。工程上,通常采用偶极子格网法进行升力面非定常气动力的计算

式中,D为气动力影响系数矩阵,w为气动面元控制点处的下洗速度列阵,积分域S表示整个升力面面积。
但是,偶极子格网法只能得到频域形式的气动力,时域响应分析时,应将频域气动力转换到时域空间。一般采用有理函数拟合技术将频域气动力扩展到Laplace域,然后采用Laplace反变换即可得到时域空间的气动力。本文采用最小状态法对频域非定常气动力进行有理函数拟合[8]

式中,p=sL/V,为无量纲的 Laplace变量;A0,A1,A2,D,E分别为多项式系数矩阵;I为单位矩阵;R为气动力滞后系数矩阵。
假设飞机升力面运动为谐振荡形式,用ik代替p,则气动力转化为

式中,k=ωL/V,为无量纲的减缩频率。
对于式(9),在给定的约束下,对QA(ik)进行多项式拟合,可得A0,A1,A2的表达式为

式(10)为矛盾方程组,可求其最小二乘解得到各系数矩阵。为了便于求解,在拟合过程中,一般预先给定D矩阵,求解多元方程可得A0,A1,A2,E矩阵,然后利用E矩阵进一步反解求出D矩阵,如此反复迭代,直到D和E矩阵满足最小二乘解要求。
多项式拟合完成后,进行Laplace反变换,即可得到时域形式的气动力
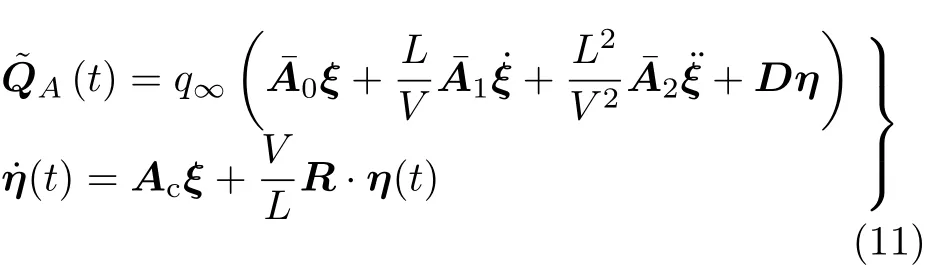
式中,Ac为气动力拟合系数矩阵,η为引入的气动力附加状态向量。
3 建模与分析
为研究间隙效应对操纵面颤振特性的影响,取某大型飞机气动弹性设计时的工程模型,进行安定面及操纵面的非线性颤振计算分析,结构模型、气动模型分别如图2和图3所示。其中,对于结构模型,安定面与操纵面之间采用弹性元连接,弹性元的刚度大小根据全机地面振动试验结果确定。

图2 结构模型
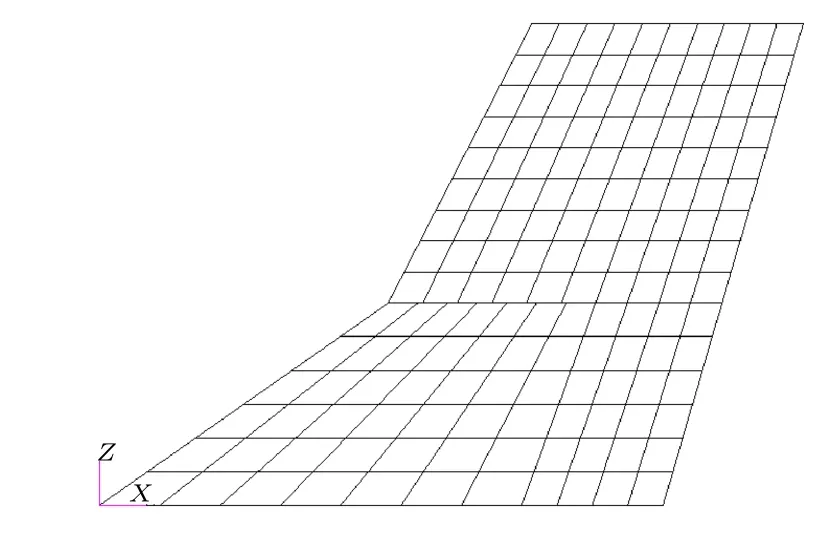
图3 气动模型
分析时,首先不考虑自由间隙,取安定面弯曲、操纵面旋转、安定面扭转模态,进行系统的时域响应分析,典型结果如图4和图5所示。
由结果可知,系统在1.46Vmax时产生了等幅振荡,且安定面弯曲、操纵面旋转模态响应幅值显著,安定面扭转模态响应幅值很小,意味着安定面弯曲与操纵面旋转相互作用引发了颤振现象,安定面扭转对系统颤振影响不大。频域分析结果表明,系统的线性颤振速度为 1.51Vmax,颤振形态为安定面弯曲与操纵面旋转耦合形式。可见,时域分析与频域分析结果吻合,本文的时域分析方法是有效的。
然后,考虑操纵面中心间隙的影响,取总间隙大小 2δs=0.25°,在给定的速度范围内,求解非线性系统的响应特性。
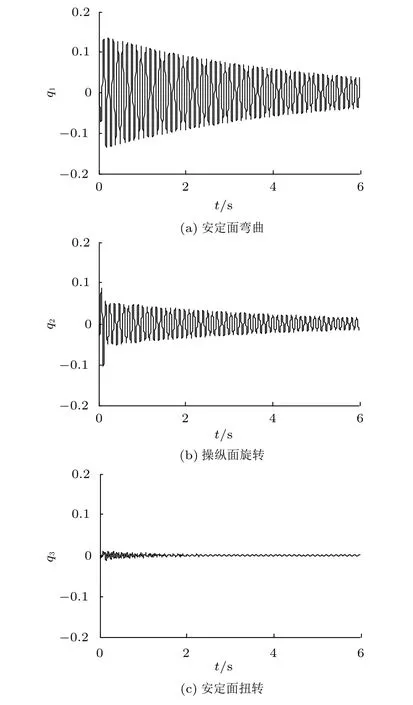
图4 V=1.43Vmax时,线性系统的广义位移响应
由于安定面扭转模态对系统颤振特性影响很小,因此主要研究安定面弯曲、操纵面旋转模态的响应特性。图6给出了操纵面存在中心间隙时,安定面弯曲、操纵面旋转模态的非线性响应历程,图7给出了对应的位移响应相平面图。由结果可知,在操纵面中心间隙的影响下,系统在V=1.23Vmax时就产生了等幅振荡,明显低于系统的线性颤振速度。
由此可见,存在中心间隙非线性的操纵面系统会发生亚临界颤振现象,即在低于线性颤振速度的某一临界速度,系统会产生极限环振荡行为,这与其他类别的非线性响应现象不同[9]。
同时,随着飞行速度的增大,系统的极限环振荡形式不变,但振荡幅值持续增大。如图8所示,在给定的三种间隙情况下,极限环幅值均随速度增大而单调增大,且在系统存在较大间隙的情况下,极限环幅值增长的幅度更大。
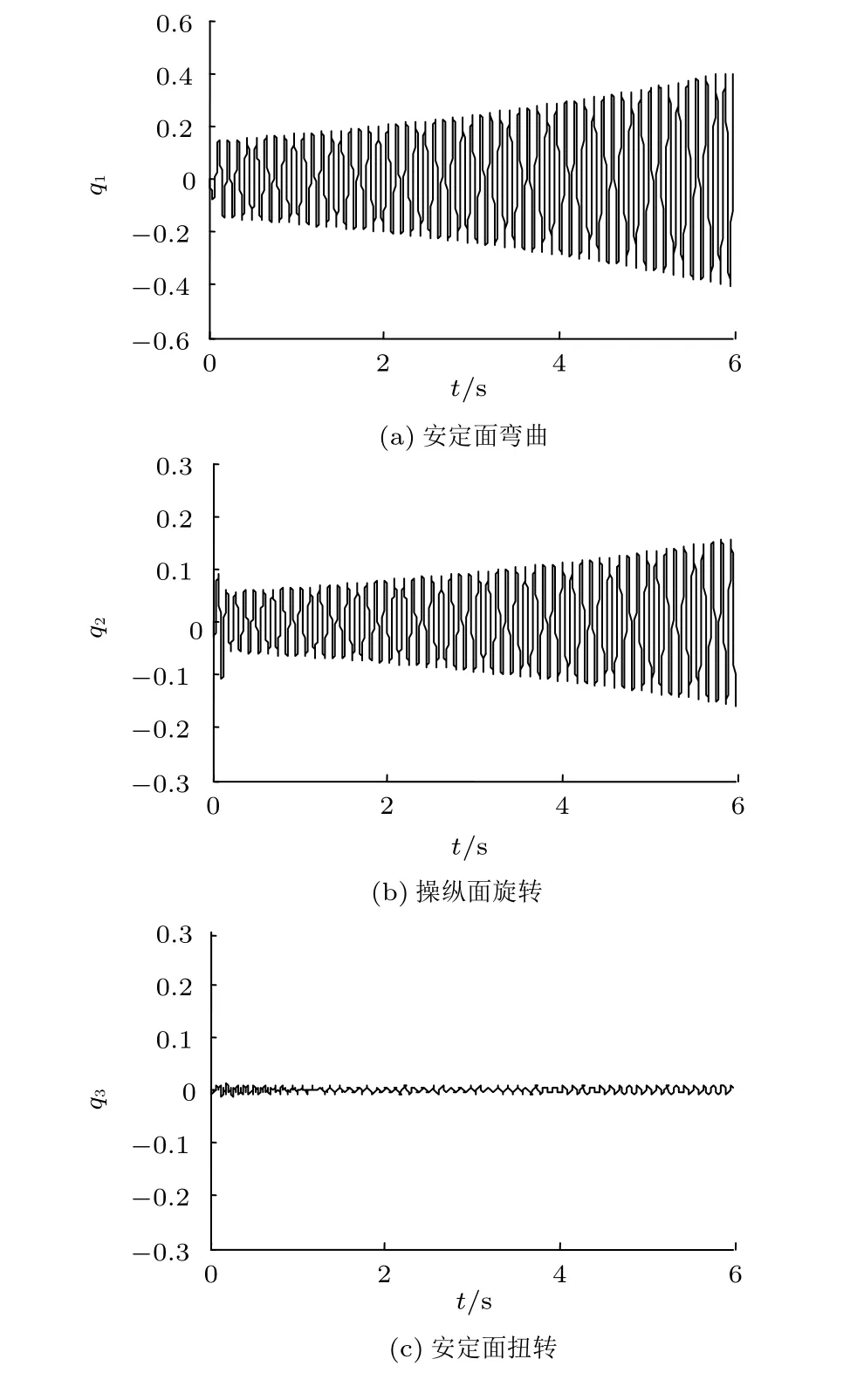
图5 V=1.50Vmax时,线性系统的广义位移响应
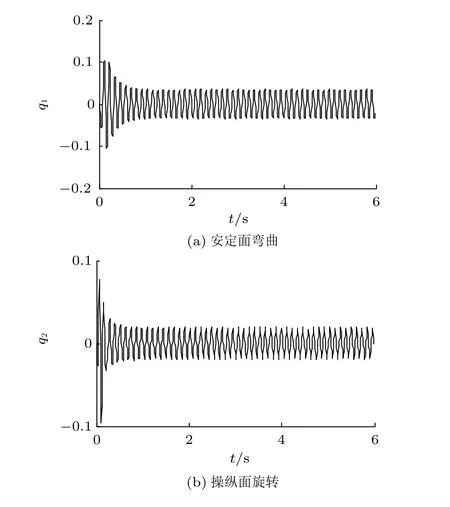
图6 V=1.23Vmax时,非线性系统的广义位移响应

图7 V=1.23Vmax时,非线性系统广义位移的相平面图
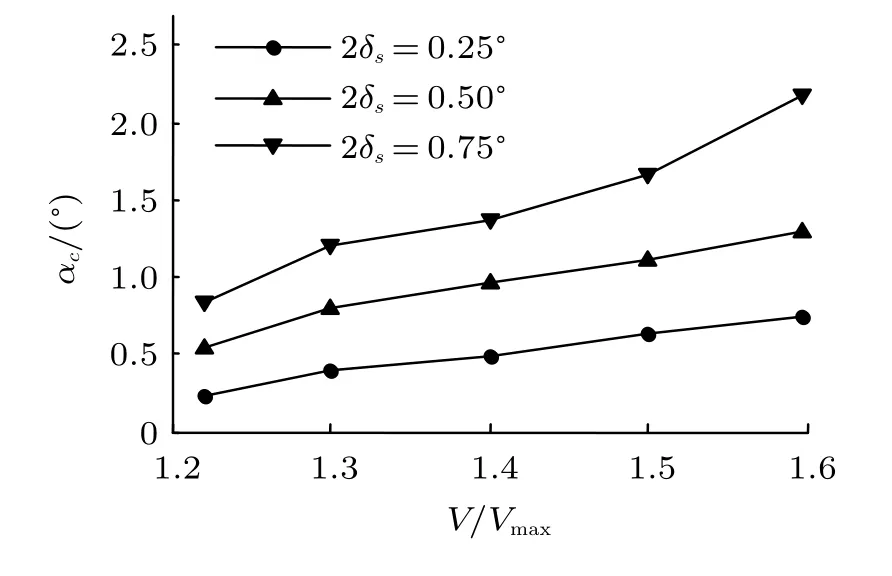
图8 极限环幅值随飞行速度的变化
飞行速度继续增大至一定程度,约为 1.64Vmax时,极限环幅值迅速发散,系统响应失稳。可见,由于极限环运动的出现,系统的发散速度得到了一定程度的提高,这与常见的非线性响应现象基本一致。
此外,飞机在试飞、服役、维护及修理过程中,由于磨损、振动及工艺因素等,操纵面的旋转自由间隙可能会增大,影响系统的稳定性。由图9所示结果可知,在不同的速度下,随着自由间隙的增大,极限环振荡的幅值也不断增大,且在系统临近失稳的大速度区域表现得更加明显。
因此,对于大型飞机,在设计阶段应严格限制操纵间隙的设计范围,在制造装配阶段严格把控工艺质量,在试飞阶段、运营阶段对间隙进行监控和定期测量,并在维护及修理过程中制定满足要求的持续保证措施,从而尽量避免飞机在飞行范围内出现极限环运动,防止引起结构失稳。
当然,近年来的部分研究也表明,对于小振幅且稳定的极限环,只要不引起结构静态或疲劳失效载荷,不导致重复性载荷产生,不引发妨碍飞机操控或造成机组人员工效性下降的有害振动,认为也是可以接受的,但振幅较大的情况则不能接受[10]。这就要求后续还应进一步开展极限环颤振对飞机正常飞行的影响研究,考虑极限环运动与结构/系统之间的诱发振荡问题,以及极限环运动对结构产生的累积损伤等,建立极限环颤振运动的安全评估方法,制定更可行、更实用的飞机操纵面间隙设计要求。

图9 极限环幅值随间隙大小的变化
4 结论
现代飞机设计过程中,都要考虑操纵面的自由间隙对飞机颤振特性的影响,并严格控制自由间隙的范围。
本文根据大型飞机的设计需要,结合飞机气动弹性设计的工程模型,考虑操纵面中心间隙的影响,采用最小状态拟合技术进行频域非定常气动力的时域转换,采用分段函数描述中心间隙引起的非线性刚度,求解操纵面在间隙效应影响下的非线性响应特性,研究操纵面极限环颤振的行为特点及其影响因素。
某型飞机安定面及操纵面的非线性颤振计算分析结果表明,在给定的飞行速度范围内,受中心间隙的影响,系统会产生极限环运动,且系统会发生亚临界颤振现象,即在低于线性颤振速度时,系统就会产生极限环振荡,这一点应予注意。同时,随着飞行速度的增大,极限环振荡形式不变,但振荡幅值持续增大,直至失稳。随着间隙的增大,同一速度下、极限环振荡的幅值也成比例地增大。飞机设计过程中,必须针对操纵面自由间隙制定严格的控制和持续保证措施。
由于飞行器颤振非线性问题的复杂性,很多问题还需进一步研究,如不同操纵面支持刚度区间、结构模态坐标的不一致性,极限环颤振运动的安全判据及评估技术等。

