基于时延优化的三维成像声呐视野展宽方法研究

杜方键，张永峰，张志正，郭小飞

(1.中国电子科技集团公司第二十七研究所，河南郑州 450047；2.郑州市水下信息系统技术重点实验室，河南郑州 450047；3.郑州宇通客车股份有限公司，河南郑州 450047)

0 引 言

水下声成像技术在水下探测尤其是海底测绘、海底物体探测与识别的应用中发挥着重要作用，具有广泛的应用前景。早期的二维成像声呐[1]仅能提供二维信息[2]，随着地形勘探、结构检查、物体测量等水下业务的迅速拓展，对立体、精细的水下成像需求愈发迫切，推动了水下三维成像技术[3]的发展进步。水下三维成像技术可快速生成水下地形、结构、物体的三维高分辨率图像，提供直观丰富的细节描述。三维成像分为近场与远场两种情形。远场条件下，波束形成的时延参数容易准确计算出来；而近场条件下，必须考虑波前弯曲程度，需要对波束形成进行聚焦处理。近场条件下，我们一般使用一种近似时延方法，通常情况下采用菲涅耳近似(Fresnel approximation)[4-5]，但是 Lawrence J.Ziomek指出，使用菲涅耳近似必须满足三个条件[6]，其中第一个条件就是限制成像声呐的有效视野范围：|θ|≤18°，这在很大程度上减小了声呐成像的效率。随着成像声呐技术的迅速发展，Andrea Trucco在1997年提出了一种基于菲涅耳近似的最小二乘近似[7]。该方法的核心是将菲涅耳近似的时延表达式进行加权，应用在线列阵中的确扩大了成像的有效视野范围，但该方法是否同样适用其它阵形的成像声呐，还需进一步研究。

本文针对平面阵近场聚焦波束形成[8-9]，研究并探讨了一种时延优化方法。该方法是在方位角和俯仰角的重新定义下，将准确的时延表达式按泰勒公式展开，取前三项，并对每一项进行加权；然后，通过求三个加权系数的偏导，再令其等于零，求出最优加权系数，此时优化的时延表达式与准确时延表达式的误差最小。优化的时延表达式不仅扩大了成像声呐的有效视野范围，而且更接近于准确的时延表达式。最后，通过计算机仿真验证了本文方法的优越性。

1 平面阵的聚焦波束形成

平面阵的布放结构如图1所示。假设有M×N个阵元组成的平面阵放置于z=0的平面，第(m,n)号阵元的坐标可以表示成v=(xm,yn,0)，其中m=1,2,…,M，n=1,2,…,N。

图1 平面阵的布放结构Fig.1 The layout of planar array

俯仰角θe与方位角θa的定义如图1所示，波束信号的方向向量可以表示为

则平面阵接收信号进行聚焦波束形成之后的输出可表示为

其中：xm,n(t)是第(m,n)号阵元接收到的时域信号；wm,n是幅度加权值；τ(r0,u,m,n)表示第(m,n)号阵元接收的距离为r0、波束方向为u的目标回波信号的时延。目标位于近场区域时，时延参数可以精确表示为

其中：c为声波传播速度，表示欧几里德范数。

由式(3)可知，在聚焦距离r0一定的情况下，第(m,n)号阵元接收目标回波信号的时延参数就是关于扫描角的函数。而成像声呐需要较宽的有效视野范围，为此，设想构造一种方法可以优化时延参数，使扫描角得以展宽。

2 时延优化算法

则精确的时延表达式可以展开为

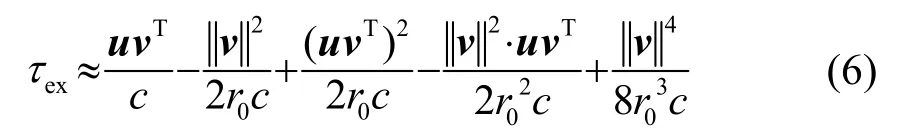
在菲涅耳近似条件下，时延表达式可表示为

其中：下标Fr表示该时延表达式为菲涅耳近似表达式。Ziomek给出了近场条件下，波束形成算法的菲涅耳近似时延表达式成立的三个必要条件，其中第一个条件是限制成像有效视野范围|θ|≤18°[6]。为了增大菲涅耳近似限定三维成像声呐的有效视野范围，在准确时延的泰勒展开表达式(6)和菲涅耳近似时延表达式(7)的基础上，采用一种优化的时延近似表达式[8-9]，如式(8)所示：

式(8)称之为TF近似，其中TF是Taylor和Fresnel的缩写，以区别于上述时延的准确表达式和菲涅耳近似表达式，k1,k2,k3是用于扩大成像声呐有效视野范围的加权系数。当k1=1,k2=−0.5,k3=0时，式(8)就等同于时延参数的菲涅耳近似表达式；当k1,k2为两个常数，k3=0时，式(8)就是文献[7]提出的时延参数近似表达式。

3 时延表达式的最优化过程

首先，引入均方差(Mean Square Error, MSE)的概念。定义两种时延的均方差为

对于τTF中的三个加权系数，若是能取到一组加权系数使得该时延更接近于准确时延，则TF近似时延表达式就是最优的时延表达式。对某一特定的成像声呐而言，它的阵元个数和阵元间距都是一定的，因此上式定义的均方误差就变成关于k1,k2,k3的函数。要使τTF最接近于准确时延τex，即要使EMS-TF最小，则可以通过求偏导来获得最优TF近似时延下的k1,k2,k3的值：

将式(10)代入式(11)可以得到：

4 仿真实验

假设有M×N个阵元组成的平面阵，M=N=48，接收信号中心频率f=300kHz，阵元间距等于信号波长，声速为1 500 m·s-1。按图1在xyz坐标系内放置平面阵。

通过求解式(3)、(7)、(9)获得菲涅耳近似下的时延均方误差。图2为在聚焦距离r0=1m处菲涅耳近似均方差随方位角φ和俯仰角θ的变化情况。图2(a)是均方差随方位角和俯仰角变化的三维图，图2(b)是图2(a)在综合方位角方向的侧视图，以下类同。从图2(b)中可以看出，当θ=18°时，均方差最大约6.8×10−14s2。

取初始K值K0=[1−0.5 0.5]，通过求解式(3)、(8)、(10)获得TF近似下的时延均方差。图3为TF近似均方差随方位角和俯仰角的变化情况。

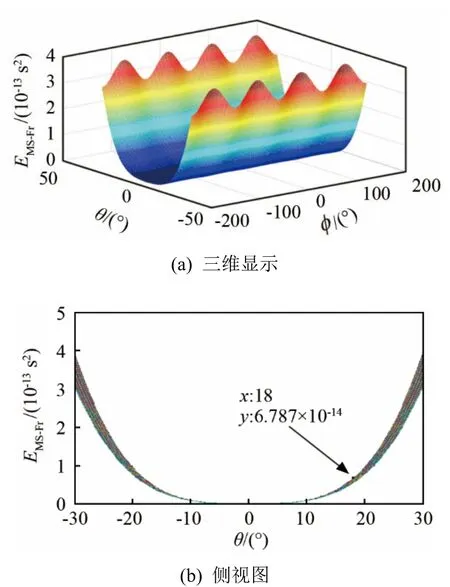
图2 菲涅耳近似的均方差Fig.2 MSE of Fresnel approximation

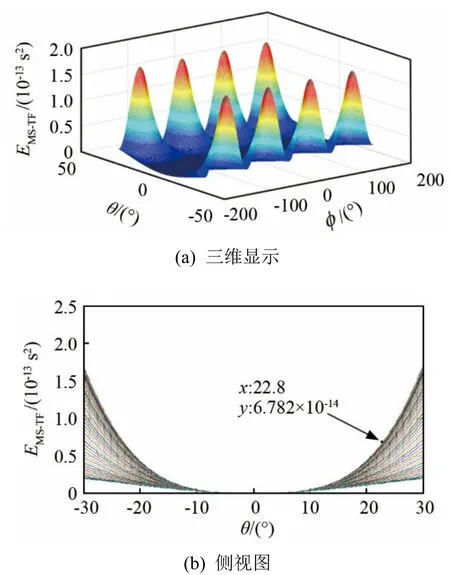
图3 TF近似的均方差Fig.3 MSE of TF approximation

对比图 3(b)与图 2(b)可知，当均方差6.8× 10−14s2时，成像声呐有效视野范围的俯仰角从±18°至少扩大到约±23°，当且仅当φ=−180°,−90°,0°,90°,180°时，有效视野范围可以从±18°扩大到±90°，说明TF近似方法可以扩大成像声呐有效视野范围。

通过Matlab计算式(13)、(15)、(16)可获得最优加权系数Kbest=[0.994 2−0.4980 0.4889]，从图4最优化后的均方差结果可以看出，均方差为6.8× 10−14s2时，成像声呐有效视野范围扩大到约±24°。相对于文献[7]提出的时延参数近似表达式，本文方法在计算时延时增加了1项多项式计算的复杂度，时延均方误差计算用时增加约 28%(2.5 s)，在实际应用过程中需要综合考虑系统资源，结合实际需求选择更为合适的时延参数近似表达式。

图4 最优化TF近似的均方差Fig.4 MSE of optimal TF approximation

从上述仿真结果可知，在传统方位角与俯仰角的定义下，当|θ|=18°时，菲涅耳近似与准确时延的均方误差最大为6.8× 10−14s2。本文另在新方位角与俯仰角定义下，以均方差为基准讨论菲涅耳近似与TF近似在该均方差值下的有效视野范围大小。图5视野范围图，图5(a)为三维显示图，图 5(b)为俯视图，以下类同。图5(b)中非深红色区域的均方差都小于6.8× 10−14s2，说明这些区域是成像的有效视野范围。

图6是TF近似在新方位角与俯仰角定义下的有效视野范围图。图6(b)中非深红色区域的均方差都小于6.8× 10−14s2，从图中可以看出该区域面积较图5(b)中大很多，说明TF近似的确扩大了三维成像的有效视野范围。

图7是当K值最优时的TF近似在新方位角与俯仰角定义下的有效视野范围图。

图7(b)与图6(b)的最大不同之处就是蓝色区域面积增大，总体非深红色区域面积也有所扩大。说明K值最优时，能够扩大三维成像的有效视野范围，并明显减小原有区域的均方差，对于提升图像分辨率、减小图像畸变具有重要作用。

图5 菲涅耳近似下平面阵的有效视野范围Fig.5 Effective visual field of planar array under Fresnel approximation

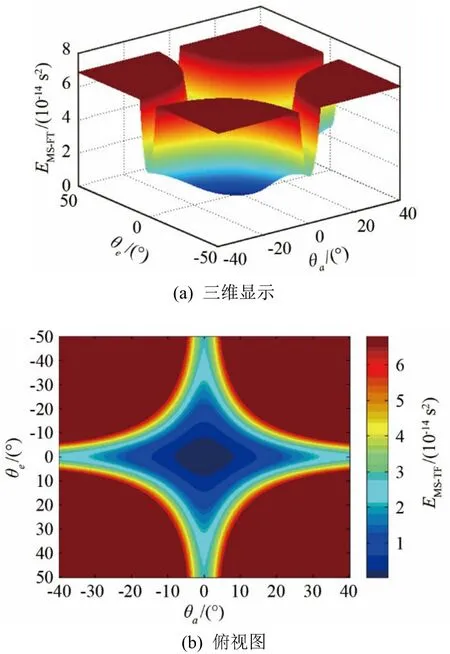
图6 TF近似下平面阵的有效视野范围Fig.6 Effective visual field of planar array under TF approximation

图7 K最优时的TF近似下平面阵的有效视野范围Fig.7 Effective visual field of planar array under TF approximation with optimal K values

5 结 论

针对平面阵，本文研究并探讨了一种时延参数的优化方法，推导了其数学表达式。通过求解平面阵在聚焦波束形成中的时延参数，并对其进行Matlab仿真，得出以下结论：

(1) 与菲涅耳近似时延相比较，本文研究的TF近似时延的确可以扩大成像的有效视野范围。

(2) 当K值最优时，TF近似时延能进一步扩大有效视野范围并明显减小原有效视野范围内的均方差。