一种信标水声定位的改进扩展卡尔曼滤波算法

刘建波，韩树平，徐景峰，杨 刚

(海军潜艇学院，山东青岛 266000)

0 引 言

信标利用水声信号对水下航行器提供导航定位服务，主要利用的是距离和方位信息。关于水声纯距离定位导航方面有较多的研究[1-4]；文献[5]将水声通信与定位导航结合，利用单程传播时延实现距离估算和定位导航。水声测距误差受多种因素影响，一般并不满足高斯噪声假设，文献[6]分析了影响水声测距系统误差的各种因素，文献[7-8]提出了基于色噪声条件下的改进卡尔曼滤波方法；文献[9-10]等提出了基于乘性噪声条件下的滤波定位算法；文献[11-12]等讨论了迭代初值对滤波的影响，提出了迭代初值的选取办法。

针对水声测距时噪声模型失配的问题，本文提出了一种缓变测距偏差模型，将测距噪声分为高斯分量和缓变非高斯分量，当两次观测间隔较小时，假定缓变非高斯分量不变。基于此，提出一种改进的扩展卡尔曼滤波(Improved Extended Kalman Filter, IEKF)算法，研究了IEKF算法的初值选取方法。仿真实验和湖试结果表明，IEKF算法能够对测距偏差进行跟踪补偿，在复杂噪声条件下定位精度明显优于常规扩展卡尔曼滤波(Extended Kalman Filter, EKF)算法。

1 基于缓变测距偏差的改进EKF

1.1 基于缓变测距偏差的改进EKF(IEKF)算法

水下纯距离导航定位时，水声测距误差与多种因素相关。利用传播时延进行距离估计，距离误差dr/r=dt/t+dc/c，时延测量误差dt与信号带宽和信噪比有关，与距离无关，在远距离测量时对测距误差影响较小。声速误差与实际水文环境有密切关系，即使利用声速剖面对有效声速进行修正，海底地形失配以及洋流等因素也会导致有效声速在不同方向和距离上的变化，增大声速误差。在收发双方距离较远时，声速在水平方向上也有可能发生较大变化，增大声速误差。一般来说，水声测距误差与距离成正比，距离越远，误差越大，但是在不同方向上，受洋流、地形等环境影响，声速误差规律可能存在不同。

假设测距噪声ξk由两部分组成：ξk=ηk+υk，其中ηk是零均值高斯噪声，υk是缓变的测距偏差，由于实际物理环境具有连续性，当前后两次观测时间间隔较短、距离较近时，认为υk的变化较小，υk=υk−1。

根据以上假设，对EKF算法进行改进，将状态向量进行扩展如下：Xk=[xkykυk]T，并将状态方程和观测方程修改为[13]

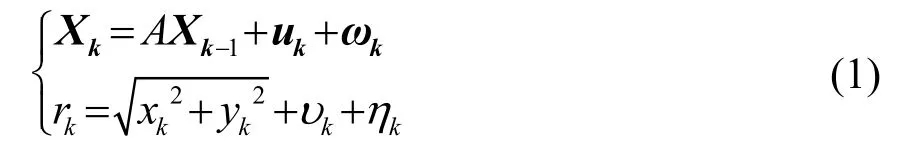
状态向量先验协方差阵P可初始化为单位阵。状态噪声协方差阵，其中主要取决于控制输入量uk的精度，水下平台一般采用航迹推算(Dead Reckoning, DR)或惯性导航系统(Inertial Navigation System, INS)获取uk，与可根据经验确定；对于，在两次观测间隔距离较近时，vk的噪声主要由状态误差与引起，，当两次观测间隔较大时，可以适当增大。

1.2 改进EKF滤波的初值确定方法

一般而言，二维纯距离定位跟踪系统满足可观测性条件[14-15]，但是机动路线和迭代初值等因素对解算收敛速度和精度有较大影响。IEKF算法与经典EKF算法相比，已知信息量不变，而扩展了状态向量，增加了未知信息υk，对算法收敛性能有不利影响，仿真显示，IEKF算法对初值比较敏感。当初值误差较小时，跟踪性能较好，系统很快进入稳定跟踪状态，当选取的初值误差较大时，跟踪性能较差，需要经过长时间的震荡才能趋于稳定。

为了减小初值对IEKF跟踪性能的影响，在进入迭代跟踪之前，不仅需要对目标进行预定位，而且需要对预定位结果进行评估，确保预定位结果具有足够的精度，才能使后续滤波尽快收敛。

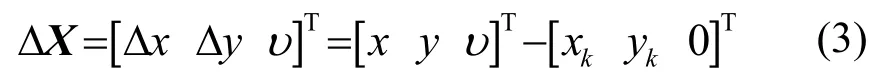
由于测距偏差υk的存在，前述估计结果仍有可能存在较大偏差，为了进一步提高预定位精度，并定量分析预定位误差的大小，对观测方程进行线性化近似，假设测距偏差在预定位期间不变，观测方程可表示为

设水下平台与浮标的距离较远，dr/r≪1，将式(4)泰勒展开并保留一阶项可得：

假设从观测伊始至完成预定位共获得k组观测数据ri,i=1,2,…k，利用[xkyk]T反推平台历史位置，获得如下线性回归方程：

其中：Y=[Y1Y2…Yk]T，X=[X1X2…Xk]T，η～N(0,σ2)，Xi、Yi与[xiyi]T以及ri的关系与式(6)形式相同。设式(7)中的线性回归方程的最小二乘解为

式中，Var(⋅)表示求向量的协方差。根据文献[16]中定理，预定位均方误差可表示为

当α≫1时，预定位结果误差较大，不足以采信，当α≈1时，预定位误差与测距噪声误差相近，可以作为后续滤波的初值。

2 仿真实验与湖试结果分析

2.1 仿真结果与分析

仿真实验中，水下平台绕浮标运动，每隔一定时间向靠近浮标的方向转向一次，转向角度随机，水下平台一个典型的轨迹如图1(a)所示。测距误差ξk由高斯白噪声ηk和缓变测距偏差vk组成。其中E(ηk)的均值为0、方差为5 m。υk分为两部分，一是声速误差引起的与距离成正比的乘性偏差γrk，γ为声速误差，一般不超过 1%；二是缓变随机偏差µk+ρ，µk为零均值随机偏差，可以通过低通滤波器对高斯白噪声滤波进行模拟，ρ为随机偏差的均值，仿真测距误差如图1(b)所示。

预定位精度因子α随观测数据点数的变化如图2所示。

图1 水下平台航迹与测距误差Fig.1 Track and ranging error of underwater platform

在图1所示轨迹下，预定位精度因子随观测点数据的增加迅速下降，在获得约200组数据后降为1，此时平台相对浮标的方位变化约90°。

图3显示了初值偏差对常规EKF与IEKF定位跟踪的影响，图3(a)迭代初值与真值的距离误差为150 m，图3(b)迭代初值与真值的距离误差为30 m。结果显示，对于传统EKF算法，定位误差约100 m，受迭代初值误差影响较小。对于IEKF算法，当初值误差150 m时，1 000组数据后定位误差约40 m，测距偏差跟踪结果震荡，2 000组数据后渐趋稳定，当初值误差30 m时，800组数据后定位跟踪误差收敛至20 m，测距偏差跟踪稳定。

图2 预设定位精度随观测数据的变化关系Fig.2 Variation of pre-positioning precision with observed data points

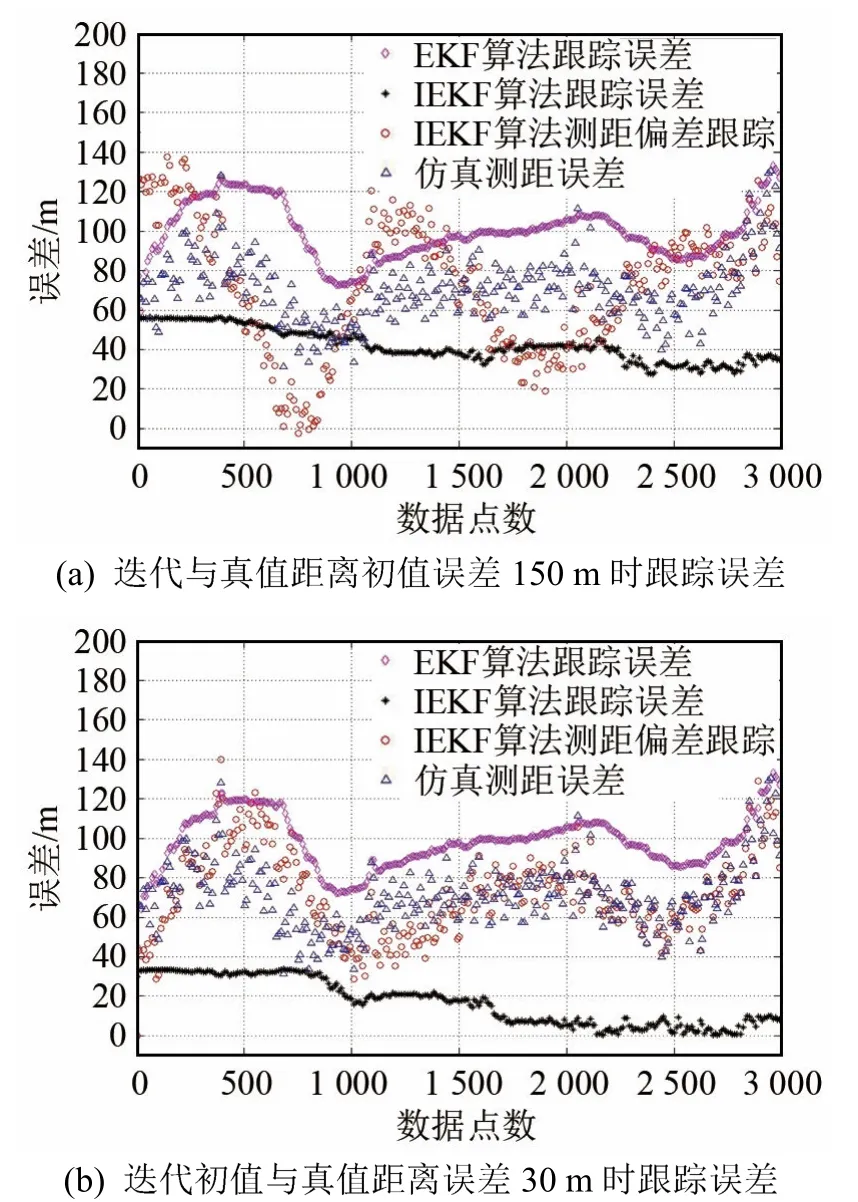
图3 预设定位精度对跟踪算法的影响Fig.3 The influence of the pre-positioning precision on tracking algorithm

图4显示了经过预定位后的跟踪结果，在预定位精度因子α低于2时进行预定位。结果显示，利用350组数据完成预定位后，定位精度约20 m，测距偏差跟踪稳定。与图3相比可以看出，在缺乏精确的位置先验信息时，预定位可以使跟踪过程更快收敛。

图5显示了基于缓变测距偏差的IEKF算法和基于乘性噪声的EKF算法[10]结果对比，可以看出两者定位误差约20 m，与常规EKF算法相比具有更高的精度。

图4 预设定位处理后的IEKF算法的跟踪结果Fig.4 The IEKF tracking result after pre-positioning processing

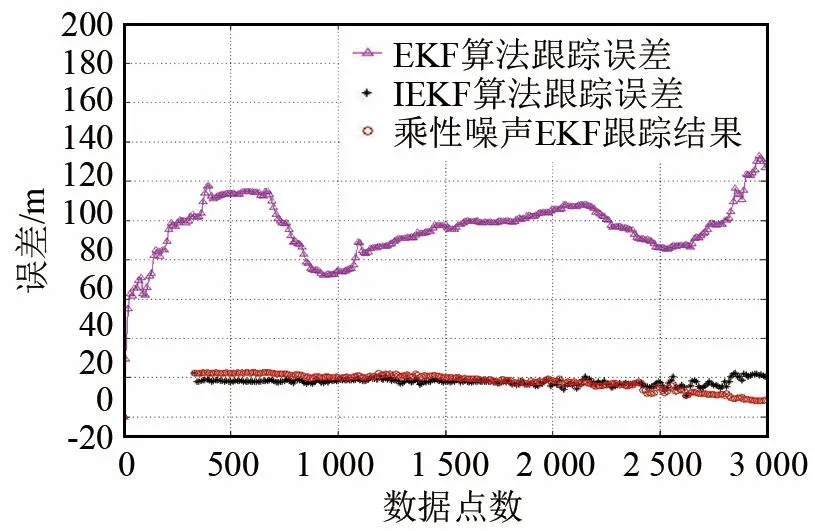
图5 基于乘性噪声的EKF算法和基于缓变测距偏差的IEKF算法的跟踪结果对比Fig.5 Comparison of tracking results between the multiplicative noise based EKF and the slow variable ranging deviation based IEKF results

为了比较IEKF算法和基于乘性噪声的EKF算法的计算结果，在测距误差ξk总方差固定的条件下，为乘性偏差γrk和随机偏差µk分配不同比例的方差，比较两种算法稳定跟踪性能，不同条件下300次蒙特卡洛仿真结果如图6所示。当噪声总方差固定时，IEKF算法性能比较稳定，与γrk和µk的相对大小基本无关，而基于乘性噪声的EKF算法性能与γrk和µk的相对大小有关，随机偏差µk方差在ξk总方差中占比小于25%时，基于乘性噪声的EKF算法表现优于IEKF算法，反之则IEKF算法性能更优。注意γrk方差与声速误差γ和距离rk的变化有关。在距离变化较小、能够获取实时声速剖面、对声线弯曲进行精确补偿的条件下，乘性偏差γrk较小，受海底地形、洋流等环境因素影响的随机偏差µk较大，IEKF算法具有更好的性能。

图6 噪声总方差恒定时两种算法跟踪性能对比Fig.6 Comparison of tracking performance of the two algorithms for a certain total variance of noise

2.2 湖试结果与分析

为了检验IEKF算法的有效性，利用2018年某水域进行的测距定位试验数据对算法进行了验证，分别利用 EKF算法、IEKF算法和乘性噪声 EKF算法进行定位。试验中用两条船分别搭载水声信号发送和接收系统，并实时记录收发船只全球卫星导航系统(Global Navigation Satellite System, GNSS)位置。试验中，发射系统将自身GNSS数据利用水声扩频通信方法发送至接收系统。接收系统利用自身GNSS数据推算自身位移，模拟DR或INS系统的位移控制量ukr，利用发射系统 GNSS数据推算发射系统位移信息uks，整个系统可等效为固定浮标和移动平台的定位跟踪问题，位移控制输入量uk=ukr−uks。

图 7显示了试验期间收发船只位置和相对态势。受试验场地和条件所限，试验期间，信号发射系统在四个方位上各发射一组信号，没有进行长时间连续机动发射，其中第1、2组相对方位约50°，第3、4组相对方位约320°，方位差约90°。

图7 收发船只的全球卫星导航系统(GNSS)相对位置Fig.7 GNSS relative positions of transmitting and receiving boats

图8显示了4组信号的GNSS距离和水声测距结果。各组数据收发距离相近，测距噪声各不相同，与距离的关系较小。

图8 收发船只实际距离与估测距离Fig.8 The actual and estimated distances between the transmitting and receiving boats

试验数据处理结果如图9所示。图9(a)显示了不同算法定位结果，图9(b)显示了IEKF算法估算的υk与实际测距误差的对比。

从图9可以看出，IEKF算法经过预定位后，定位误差约10 m，EKF算法定位误差收测距噪声影响，在10～40 m范围内波动，IEKF算法性能明显优于EKF算法，能够较好地跟踪和补偿测距缓变偏差。

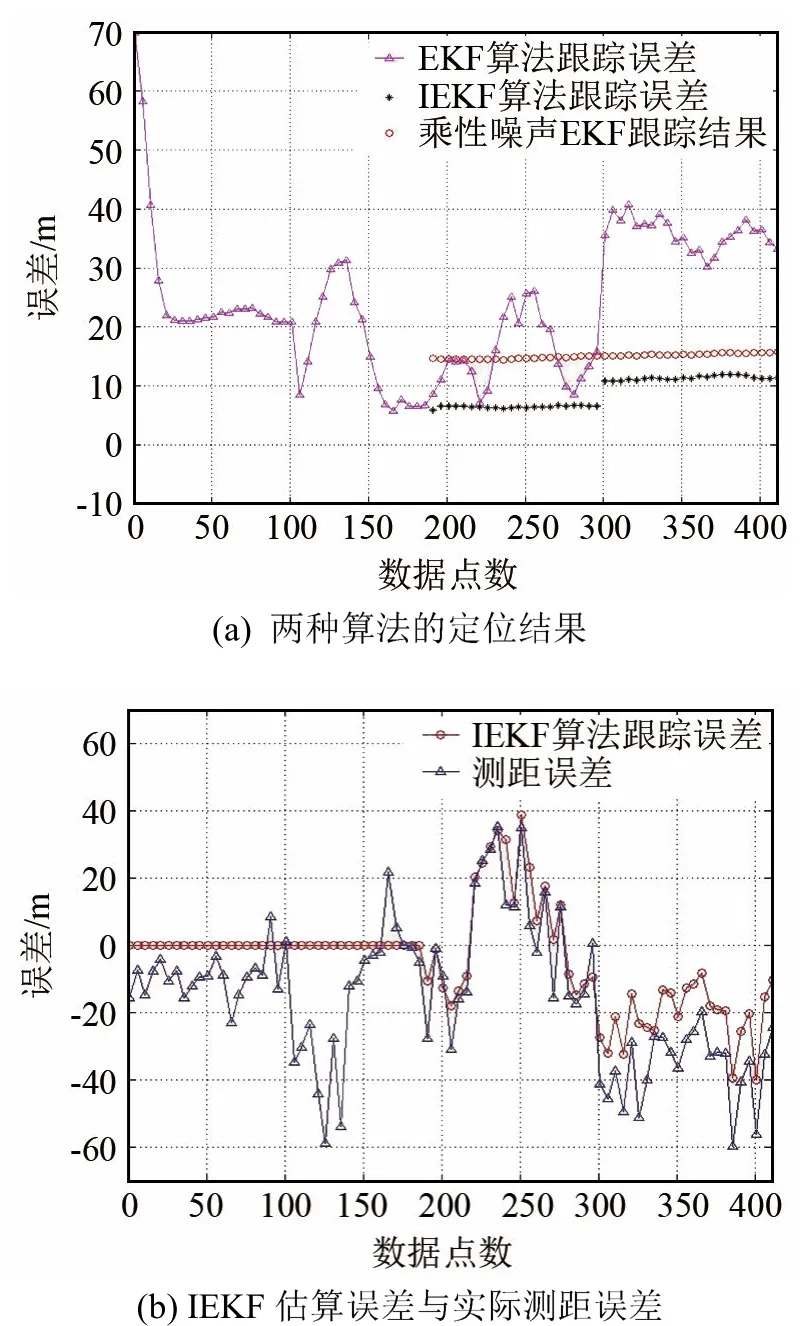
图9 湖试数据处理结果Fig.9 The processing results of lake trial data

3 结 论

本文提出了一种基于缓变测距偏差的改进EKF(IEKF)算法，将水声测距误差分为缓变偏差和零均值高斯噪声两部分，并通过对缓变偏差的跟踪与补偿，减小测距噪声模型失配对EKF的影响。仿真实验和湖试结果表明，本文提出的迭代初值选取方法能够使IEKF算法实现对缓变测距偏差的跟踪补偿，当缓变随机偏差在总方差中的占比较大时，性能优于基于乘性噪声的EKF算法。