基于粒子群算法的水声通信网络能量优化方法
李朋伟,孟 荻,陈 倩
(海军研究院,北京 100161)
0 引 言
水声通信网络(Underwater Acoustic Communication Network, UACN)在海洋及相关技术领域具有重要地位,可广泛应用于海洋科学研究、气象水文数据采集、重点海域监测、威胁目标警戒跟踪等领域,发展前景广阔[1]。但目前水声通信网络的发展水平与应用需求还有较大差距,其中,能量问题一直是影响水声通信网络发展应用的重要因素,而发展水下节点能量采集功能[2]和节点发射功率控制功能是解决水声通信网络能量问题的重要发展方向。
本文针对节点具备发射功率控制功能的网络如何降低网络节点总功耗,减缓网络中节点死亡速率开展研究。对于固定节点,相比于节点电路功耗,节点上水声换能器的功耗更大。因此,研究如何进行节点功率分配可有效降低节点发射功耗[3]。本文基于在满足一定接收信噪比条件下的节点发射功率与传输距离的非线性关系,研究如何通过优化节点信息传输路径,达到降低网络节点总功耗的目的。
网络分簇[4]是降低网络节点总功耗、实现网络能量优化的有效方法之一。文献[5-6]针对最优分簇问题,提出LEACH、LEACH_L等分簇方法。文献[7]结合水声通信网络节点功耗特点,基于节点担任簇首次数、节点剩余能量及节点相对位置关系等,提出动态分簇方法,通过周期性轮换簇首,一定程度上降低了节点功耗,延缓了首个节点的死亡。文献[8]通过引入水下节点发射功率与传输距离的关系,改进优化算法,进一步降低网络节点总功耗。但在上述能量优化方法中,作者设定了簇首的最优数量,网络中存活节点数量不断减少,最优簇首数量始终不变。此外,按照上述所提优化方法,网络采用周期性选簇,在每一个网络周期开始前均需重新选簇,频繁选簇带来了大量的额外能量消耗。
分簇网络中的簇首可视为节点采用两跳路径向目的节点发送信息时的中继节点,因此,本文基于网络中存活节点数量和节点剩余能量的变化情况,自适应确定中继节点数量及中继节点位置的最优方案,进而节点基于自身到不同中继节点和目的节点的发射功耗,确定最优传输路径。此外,针对优化过程带来的额外能量损耗,本文改进了网络模型,该模型采用事件触发的方式启动优化过程,减小了优化过程带来的能量损耗。仿真结果表明,本文所提算法可有效降低网络节点总功耗,延缓首个节点的死亡,减缓网络中节点死亡速率,从而减缓网络有效覆盖面积随着网络运行而减小的速率。
1 节点能耗模型[8]
声呐方程描述了发射声源级(LS)、传播损失(LT)、背景噪声级(LN)、接收指向性(DI)及接收端信噪比(RSN)之间的关系,表达式为[9]

声源级LS定义为

式中:Itrans表示距发射换能器声学中心标准距离处的声源强度。Iref为参考声强,其值为0.67×10-18W·m-2。则节点发射电功率[9]为
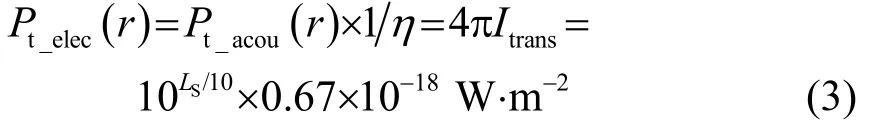
其中:Pt_acou为发射换能器声功率,η为发射换能器的效率。
传播损失[9]LT为
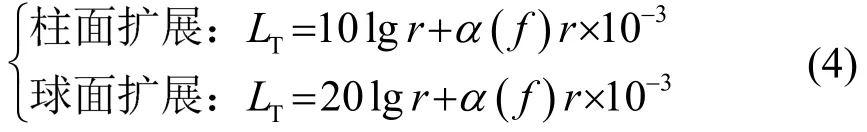
其中:r是通信距离,单位m;α(f)是声信号吸收系数,单位dB·km-1,对于吸收系数,Thorp给出适用于低频段的公式[10],表达式为

在满足接收信噪比的条件下,依据式(1)~(5),图1给出了发射端最小发射电功率与通信距离的关系(柱面扩展,DI=0,LN=65 dB,LS=20 dB )。从图1中可以看出,最小发射功率与通信距离呈非线性关系,距离越远,最小发射功率增长越快。因此节点采用两跳或多跳的方式向目的节点发送信息时,整个路径上节点的功耗可能低于节点直接向目的节点发送信息的功耗。Stojanovic[11]的研究也表明,采用短距离多跳实现中远距离水声通信可获得比单跳更低的节点发射功率。

图1 最小发射功率与通信距离关系Fig.1 Relationship between the required transmission power and the communication distance
在水声换能器发射能耗基础上,将节点的电路能耗加以考虑,发射端能量消耗可建模为

其中:RB表示信息传输速率,单位为bit·s-1,Eelec为发射换能器电路处理1 bit数据消耗的能量,k是发送信息量。
2 网络模型
本文研究的水声通信网络由一个水面网关节点和若干水下节点组成,水下节点通过单跳或两跳方式将信息传输到网关节点。水声通信网络进行过程如图2所示。
运行过程分两个阶段:路径优化阶段和稳定运行阶段。在路径优化阶段,网关节点运行第3节所提路径优化算法,确定每个节点在网络中的角色:中继节点或普通节点,进而确定节点的最优信息传输路径。普通节点指具备一定功能如水温监测的节点;中继节点除具备普通节点的功能外,还负责接收普通节点的信息并转发到网关节点。路径优化完成后网络进入稳定运行阶段。在该阶段,普通节点通过分配的中继节点向网关节点发送信息(两跳),中继节点直接向网关节点发送信息(单跳)。网络每经历一次稳定运行阶段,称为一个周期。

图2 水声通信网络运行过程Fig.2 The operation process of underwater acoustic communication network
触发网络进入路径优化阶段的条件有两个:(1)网络中是否存在中继节点的能量小于初始值的a%或是否出现死亡节点;(2) 是否存在中继节点的能量大于初始值的a%或是否出现死亡节点(a用于判断节点是否可作为中继节点的候选节点,当节点当前能量小于初始能量的a%时,认为该节点剩余能量较少,不宜再承担能耗较大的中继节点角色)。针对所提水声通信网络模型,提出如下假设:
(1) 网关节点部署在区域中心且能量充足;
(2) 网关节点负责路径优化方案生成并将方案发送到每一个节点;
(3) 节点的初始能量相同且具有发射功率控制功能;
(4) 稳定运行阶段每个节点发送的信息量相同;
(5) 中继节点对接收的信息直接转发,不处理;
(6) 节点采用水声换能器进行信号发射和接收。
3 路径优化算法
3.1 目标函数
路径优化的目的是降低网络节点总功耗,减缓网络中节点死亡速率,因此本文引入网络中所有存活节点的发射总功率作为优化目标函数,表示为
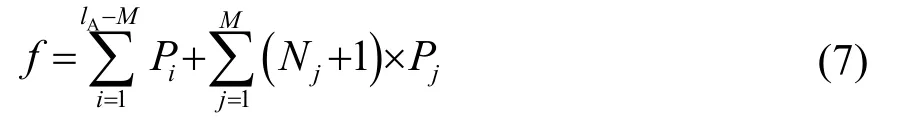
其中:lA为网络中的存活节点总数,M为担任中继角色的节点数量。Pi为第i个普通节点的最小发射功率,Pj为第j个中继节点的最小发射功率,Nj为以该节点为中继节点的普通节点数量。网络中担任中继角色的节点数量不同和不同节点担任的角色方案不同,即每一个节点的信息传输路径不同时,对应的目标函数值不同,目标函数值越小,表明网络中存活节点的发射总功率越小。通过优化网络中所有存活节点担任角色的方案和担任中继角色的节点数量,可使所有存活节点的发射总功率最小。
3.2 优化算法
在路径优化阶段,网络中不同节点担任何种角色有多种组合方案,以3.1节中的目标函数为优化目标函数,从众多方案中选择出最优方案的过程可建模为寻优过程。对于该过程,粒子群算法以一定数量的方案为基础,通过最优搜索,寻优获得目标函数值最小时对应的优化路径方案,该方案即是最优方案。相较于穷举算法,粒子群算法的优点是优化效率高,获得最优结果的时间更短。
以PSj表示第j个节点的角色,则所有节点的角色按照节点序号排列所形成的组合(lA为网络中存活节点总数)可视为粒子群中的一个粒子,粒子群中的第i个粒子为,i=1…N(N为粒子群规模)。以3.1节中目标函数为粒子的适应度函数,利用粒子群算法获得的最优粒子对应的节点角色方案即是最优节点角色方案。在最优角色方案的基础上,普通节点基于自身到不同中继节点和网关节点的发射功耗,确定是采用某一个中继节点转发信息,还是采用单跳方式向网关发送信息,由此即可获得每一个节点的最优信息传输路径。
本文在文献[8]中基于改进的粒子算法的基础上,综合考虑网络运行不同阶段存活节点的数量,改进粒子群的初始化方式和变异算子,将自适应交叉概率和变异概率引入该算法中,形成新的优化算法,获得较好的优化结果。算法流程如图3所示。

图3 能量优化算法的流程图Fig.3 Flowchart of the energy optimization algorithm
(1) 粒子编码
(2) 粒子群初始化
随着水声通信网络运行,网络中存活节点数量lA在不断减少,因此应在路径优化阶段根据存活节点数量,在粒子群中自适应产生中继节点数量的所有可能方案,即产生的粒子中中继节点的可能数量为1~lA。本文采用轮换方式,依次产生中继节点数量为1,2…lA的粒子,假设粒子群规模为N,则中继节点数量分别为1,2,3…lA的粒子数量依次为

对于中继节点数量为T的粒子,随机选择T个节点,将节点在粒子上对应的位置标记为1,死亡节点标记为−1,普通节点标记为0,不能作为候选中继节点标记为2。完成粒子生成后,依次计算每个粒子的适应度值,并初始化历史最优粒子(记为)和全局最优粒子(记为)。
(3) 自适应交叉概率和变异概率
采用正比选择策略[12]。设粒子与历史最优粒子交叉的初始交叉概率为PH0,按照式(9)获得自适应交叉概率:

式中:Fit为粒子和其历史最优粒子两者中较大的适应度值,Fit,avg为每代种群与待交叉的历史最优粒子组成的新群组的平均适应度值,Fit,max为新群组中最大的适应度值。
设粒子与全局最优粒子交叉的初始交叉概率为PA0,按照式(10)计算自适应交叉概率:

式中:Fit为粒子和全局最优粒子两者中较大的适应度值,Fit,avg为每代种群与全局最优粒子组成的新群组的平均适应度值,Fit,max为新群组中最大的适应度值。
初始变异概率为Pm0,按照式(11)计算获得:

式中:Fit'为待变异个体的适应度值。
(4) 交叉算子
交叉算子与文献[8]所提的交叉算子一致,当粒子与历史最优粒子交叉时,需完整交叉含有两个中继节点的粒子片段,当粒子与全局最优粒子交叉时,需完整交叉一个中继节点。
(5) 更新历史最优粒子和全局最优粒子
用历史最优粒子和全局最优粒子与粒子群中的粒子交叉获得新粒子后,对粒子的历史最优粒子和全局最优粒子进行更新,将产生的较优粒子保存。
(6) 变异算子
对每一个粒子,在该粒子上随机选择一个节点,当该节点标记为1时,将其变异为0;当该节点为0时,将其变异为1;当该节点为−1或2时,不变异。变异完成后,计算新粒子的适应度值,如果新粒子的适应度值优于变异前,则用新的粒子替换变异前的粒子,并更新该粒子的历史最优粒子,否则不更新变异前的粒子。粒子群变异完成后更新历史最优粒子和全局最优粒子。
4 仿真分析
采用Matlab2015a进行仿真。文献[8]将所提算法与文献[7]所提改进粒子群算法以及LEACH算法进行对比,仿真结果表明,文献[8]所提算法可获得更优的分簇结果,进一步降低了网络节点总功耗,减缓节点死亡速率。本文将所提能量优化算法与文献[8]所提算法进行对比。两种方法的主要参数设置如表1所示。

表1 本文及文献[8]中能量优化算法主要参数设置Table 1 The main parameter setting for the energy optimization algorithms in this paper and in the reference[8]
本文算法其他仿真参数为PH0=0.9,PA0=0.9,Pm0=0.8。文献[8]所提方法的其他仿真参数按照其给出的值,为a=0.5,b=0.25,c=0.25,c1=c2=0.1,w=0.729 8(a,b,c为文献[8]所提的目标函数中不同因素所占比重,c1,c2,ω分别为粒子与历史最优粒子的交叉概率、粒子与全局最优粒子的交叉概率和变异概率)。仿真中,节点接收信息的能量消耗模型为:Erecei=Pr_elec×(k/RB)+kEelec。
图4和图5给出了在网络初始化时利用两种方法获得的最优传输路径方案。

图4 文献[8]算法的最优传输路径Fig.4 The optimized transmission paths of the algorithm in the reference[8]

图5 本文算法的最优传输路径Fig.5 The optimized transmission paths of the proposed algorithm in this paper
图4为文献[8]算法获得的最优路径方案。在该方案中,32个普通节点被分配在4个簇中,普通节点利用簇首中继向网关节点发送信息。图5为本文算法的最优路径方案。在该方案中,有 12个节点担任中继节点,普通节点利用 1~8 号中继节点向网关节点发送信息,9~12号中继节点仅负责将自身信息发送到网关节点。在最优路径方案中,采用原算法的网络节点总功耗为0.297 9 W,而采用本文算法的网络节点总功耗为0.173 8 W,低于前者。
图6比较了采用两种算法的网络中存活节点数量随网络运行的变化情况。
图7比较了采用两种算法的网络中,网络运行时,网络剩余总能量的变化情况。由图6可知,采用文献[8]算法的网络在第333个周期时出现首个死亡节点;而采用本文算法的网络在第358个周期时出现首个死亡节点,比原算法延长 25个周期。第377个周期时,采用原算法的网络存活节点数为0,网络完全死亡,而采用本文算法的网络存活节点数为28,表明网络仍有较大覆盖面积。第718个周期时,采用本文算法的网络存活节点数降至4。综上,仿真结果表明采用本文算法可延缓首个节点死亡时间,节点死亡速率更低。
从图7中可以看出,采用本算法的网络的能量始终高于原算法,说明采用本文算法的网络的总功耗始终低于采用原算法的网络。且从图7中还可看出,在采用原算法的网络已完全死亡时,采用本文算法的网络的剩余总能量仍有1.376× 104J。
此外,粒子群规模N和种群繁殖代数MG影响粒子群算法的收敛速度、搜索结果与最优结果的逼近程度。N和MG取值较大时,虽然能获得较优的搜索结果和较好的算法稳定性,但是搜索时间长,搜索效率低;N和MG取值较小时,会导致算法搜索结果不收敛。因此,粒子群规模和种群繁殖代数存在最优取值,而该值与节点数有关。取值原则一般为节点数越多,则粒子群规模和种群繁殖代数的最优取值越大。
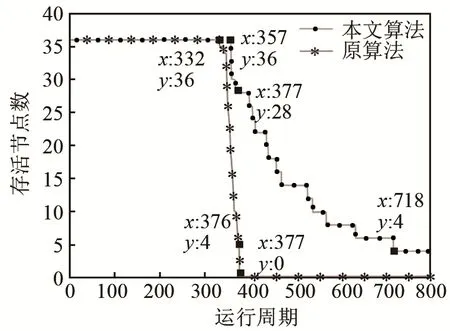
图6 两种算法存活节点数量的对比Fig.6 Comparison of the number of alive sensor nodes for the two algorithms

图7 两种算法网络剩余能量的变化情况Fig.7 Comparison of the residual energy in the network for the two algorithms
因此在本文所述网络中,随着网络运行,存活节点数在不断变化,粒子群规模和种群繁殖代数的最优取值应是自适应变化的,自适应变化关系需作进一步详细研究。为分析方便,本文仅考虑了随着网络运行,粒子群算法规模和种群繁殖代数取值不变的情况,采用蒙特卡洛仿真方法,表2、3给出了网络中节点数为36个时,粒子群规模和种群繁殖代数取不同值时,算法搜索结果对应的网络总功耗的均值和方差变化情况。
从表2、3中可知,在N=200时,当种群繁殖代数MG大于80,搜索结果均值保持不变,方差为0;在MG=100时,当粒子群规模N大于20,搜索结果均值保持不变,方差为0。因此当N=200,MG=80,或N=20,MG=100,算法均可获得最优值,且搜索效率较高,当N和MG选取更大值时,算法也可获得最优值,但搜索效率会下降。若需对搜索效率有进一步要求,可对N、MG的不同取值进行精细化仿真,获得更精确的取值。

表2 种群繁殖代数的影响(N=200)Table 2 The influence of the generations of population reproduction (N=200)

表3 粒子群规模的影响(MG=100)Table 3 The influence of particle swarm size (MG =100)
5 结 论
本文针对水声通信网络能量优化问题,通过改进水声通信网络模型,采用事件触发的方式触发网络进入路径优化阶段,从而降低了网络优化阶段的额外的能量消耗。并通过在网络路径优化阶段引入改进的粒子群算法建立优化算法,寻优获得网络中各个节点的最优信息传输路径,以降低网络节点的总功耗。仿真结果表明,本文所提优化方法能有效降低网络节点总功耗,延长首个节点死亡时间,减缓网络中节点死亡速率,从而减缓了网络有效覆盖面积随着网络运行而减小的速率。

