重载货车-固定辙叉动态与静态接触性能分析

马 贺, 牛 岩, 邹小春, 张 军, 于 淼

(1.北京建筑大学机电与车辆工程学院，城市轨道交通车辆服役性能保障北京市重点实验室，北京 102616；2.中车大连机车车辆有限公司科技管理部，大连 116022)

近年来，重载铁路的运输条件一般为大轴重、大密度、交通繁忙。在如此恶劣的运输环境下，道岔的损坏尤为严重。其中固定辙叉更换周期平均为3～4个月，这不仅带来了大量的经济损失，还显著增加了养护维修工作量[1-3]。

目前对于轮轨关系的研究有了很大的进展，一般是通过有限元软件和动力学软件仿真计算、数值分析和实验的方法进行研究。其中袁雨青等[4]运用有限元计算的方法分析了踏面磨耗对轮轨接触特性的影响。陈艳玮[5]利用动力学软件研究了轨道参数对小半径曲线钢轨侧磨的影响。而针对重载铁路固定辙叉的快速磨损问题，中外专家学者也进行了大量研究。陈嵘等[6]、郭利康等[7]建立了三种不同有限元模型，计算和分析三种辙叉在极限荷载和疲劳荷载作用下的力学行为，对改进前后高锰钢辙叉的力学性能进行了对比分析。Wiest等[8]进行了辙叉尖端的变形和损坏分析。Pletz等[9-11]建立了心轨尖端撞击的动态有限元模型，预测了心轨早期损坏的演变。文献[12]从动力学和静力学两个方面分别对重载铁路固定辙叉型面匹配问题进行了研究，并提出了轮轨磨耗预测的新方法。

这些学者对辙叉的疲劳受力分析和辙叉的型面演变进行了研究，而并未综合考虑动力学与静态接触两方面轮叉接触状态。为此，在文献[12-13]的研究基础上，针对重载线路中固定道岔辙叉心轨磨耗严重问题，建立了重载货车LM型面车轮通过固定辙叉的动力学模型、固定辙叉不同位置处车轮与辙叉的三维弹塑性接触模型，计算分析了重载货车侧向通过固定辙叉过程中的动力学性能和轮叉之间的弹塑性接触状态。

1 动力学分析

1.1 货车与辙叉动力学模型的建立

运用多体动力学软件建立重载铁路货车-道岔系统耦合模型。其中，车体、构架和轮对具有伸缩、横向运动、浮动和下沉、侧滚、点头和摇头六个自由度，采用了转K6型转向架，如图1所示。

线路采用离散轨道/轨枕模型，轨道垫是单层支撑模型，为保持轨枕质量，将轨道和轨枕视为线路的一部分，其垂向和横向均采用弹簧-阻尼模型与地面连接。关键截面型面由Pro/E软件建立，相邻两个截面之间的参数由线性插值得到。建立的固定辙叉区模型如图2所示，其中包括固定辙叉、护轨与基本轨。

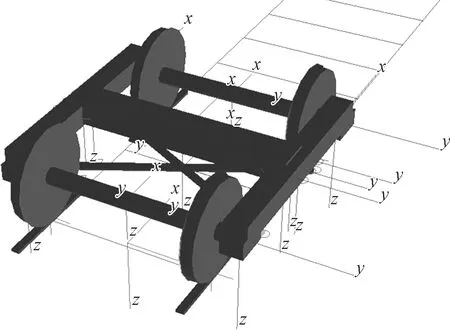
图1 转K6型转向架动力学模型Fig.1 Dynamic model of the K6 type bogie

建立货车-道岔系统耦合动力学整车模型，同时定义轮轨接触关系，如图3所示。模拟C80货车侧向通过固定辙叉，速度分别为30、40、50、60 km/h，计算并分析过叉的动力学性能。

图2 辙叉区模型Fig.2 Frog model

图3 货车-道岔系统动力学模型Fig.3 System dynamic model of wagon and turnout

1.2 车轮与辙叉接触几何关系

图4为C80货车行驶至距离理论尖端360、480 mm时，车轮与辙叉之间的接触几何关系。

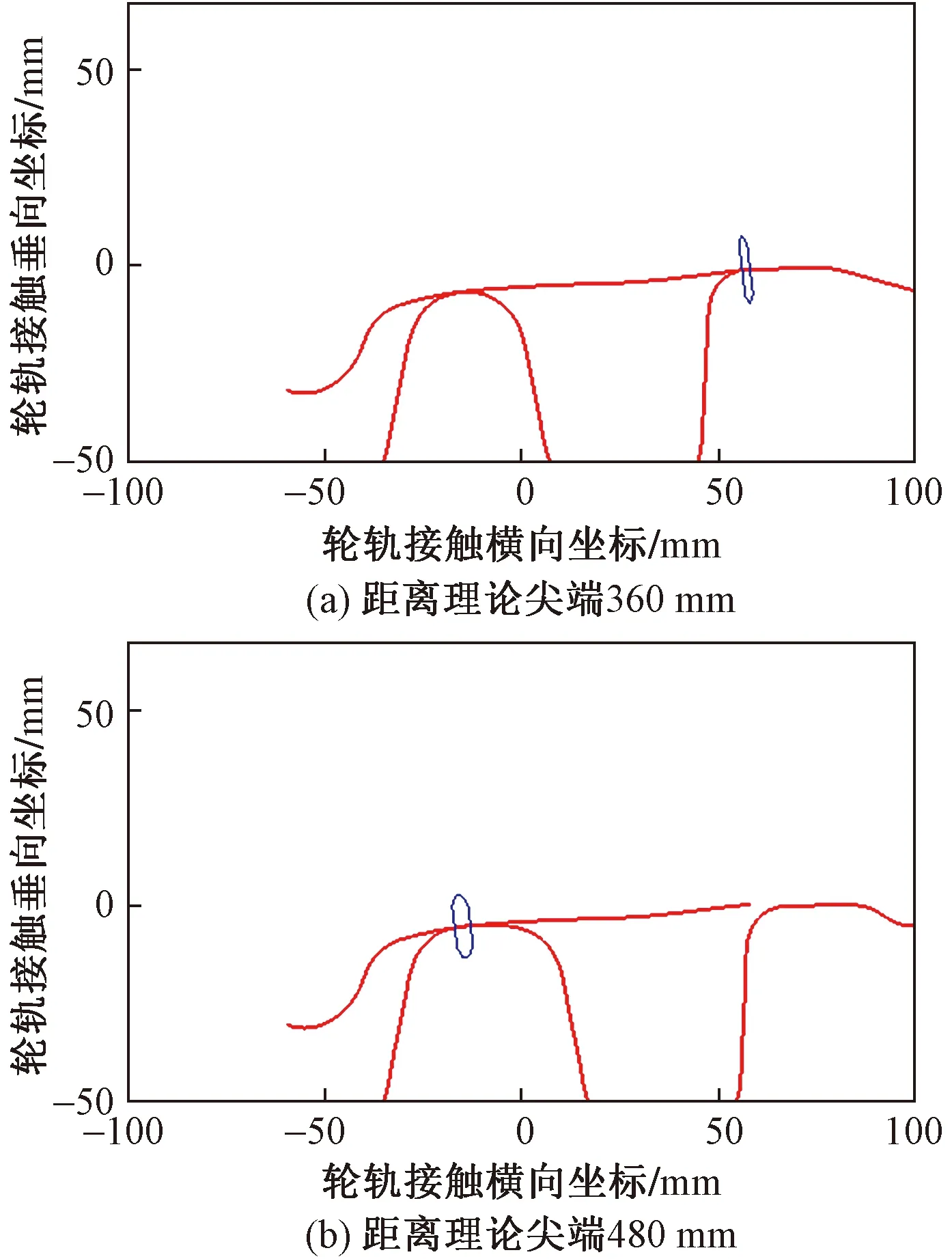
图4 车轮与辙叉型面之间的接触几何Fig.4 Contact geometry between wheel and frog profiles

由图4可知，标准货车LM车轮在距离理论尖端360 mm时只与翼轨接触，当距离理论尖端480 mm时仅接触心轨，这说明在距离理论尖端360～480 mm会出现车轮与翼轨和心轨同时接触的情况。由于车轮型面是磨耗型，当车轮与辙叉的翼轨和心轨同时接触时，同一车轮上同时存在两个不同的滚动圆半径。在某一瞬时车轮的角速度是恒定的，车轮与辙叉之间必然出现相对滑动，这导致车轮与辙叉磨耗加剧。

1.3 磨耗功率分析

磨耗功率代表消耗在轮轨接触面上的功，能够直接反映车轮型面的耐磨性能。磨耗功率与轮轨间的磨损成正比，常用来评价轮轨之间的磨耗程度。图5所示为C80货车在不同速度下侧向通过重载道岔固定辙叉时车轮从翼轨过渡到心轨瞬间的磨耗功率变化情况。

图5 不同速度下的磨耗功率Fig.5 Frictional power at different speeds

从图5中可以看出，磨耗功率随货车速度的增加变化较大。当货车侧向通过固定辙叉的速度为30 km/h时，车轮与辙叉之间的磨耗功率为552.497 N·m/s；当过叉速度为40 km/h时，磨耗功率为776.496 N·m/s，与时速30 km/h时的相差较少；当货车时速增大到50 km/h时，磨耗功率增至7 873.46 N·m/s，其数值比40 km/h时增大了9倍多；当货车速度增大到60 km/h时，其磨耗功率高达40 750 N·m/s。由此可见，为了降低车轮与辙叉之间的磨耗，一定要严格控制货车侧向通过辙叉时的速度，建议控制在50 km/h之内。

1.4 滚动圆半径与垂向力分析

滚动圆半径是描述车轮与轨道接触的主要特性之一，车轮与钢轨接触点与车轴中心线的距离定义为车轮实际滚动圆半径。标准货车LM型面车轮为磨耗型，其滚动圆半径的变化表示车轮接触位置改变，轮轨接触状态发生变化。图6为C80重载货车侧向通过固定辙叉过程中从理论尖端到向心轨方向2 m范围内车轮滚动圆半径的变化。

图6 滚动圆半径的变化Fig.6 Variation of rolling radius

图6显示的是在时速30 km/h时车轮通过辙叉过程中滚动圆半径的变化情况，其他运行速度下与其变化趋势基本相同。在距离理论尖端400 mm处车轮首先与心轨接触，接触瞬间将对心轨产生冲击。在距离理论尖端460 mm处车轮滚动圆半径突然增大到420.5 mm，此时车轮踏面内测与心轨接触，随着车轮继续前进，逐渐变成车轮踏面的中间部位与心轨接触，滚动圆半径值逐渐减小，最后趋于稳定。

C80货车在处于满载静止状态时，其轴重为25 t，分担在每个车轮上的垂向载荷为125 000 N。在货车通过辙叉时，由于固定辙叉不可避免地出现“有害空间”，当车轮从翼轨过渡到心轨时，车轮对心轨产生一定的冲击作用。表1所示为当车轮以不同速度与翼轨和心轨接触时的滚动圆半径以及辙叉心轨上所受的最大垂向力。

表1 不同速度下的滚动圆半径与垂向力

从表1中可以看出，在不同的运行速度下，车轮与翼轨之间接触点处的滚动圆半径约为415 mm，心轨接触点处的滚动圆半径约为420 mm，两者之间的差值约为5 mm。因此可以得出，速度对车轮滚动圆半径几乎没有影响。

在货车通过辙叉的过程时，轮叉之间的动载垂向力均大于静载轴重时的125 000 N。当运行速度增加时，轮叉之间的垂向力不断增大，当货车速度达到60 km/h时，辙叉心轨所受的垂向力为565 551 N，是静载轴重时的4.5倍，这对心轨影响更大，使得心轨磨损严重。

2 弹塑性接触分析

2.1 车轮与辙叉弹塑性接触模型

在固定辙叉不同位置处，应用标准LM型车轮和75 kg/m钢轨12号固定辙叉建立车轮与辙叉的三维实体模型。车轮的三维模型通过二维网格绕车轴中心线旋转得到，辙叉三维模型由变截面拉伸得到，轮叉三维有限元接触模型如图7所示。采用标准轨距1 435 mm，轮缘内侧距为1 353 mm。

图7 轮叉三维有限元接触模型Fig.7 Three-dimensional finite element contact model of wheel and frog

将三维接触模型导入到大型计算软件Marc中，施加载荷与约束。钢轨底部全约束，车轴两端约束横向和纵向方向上的位移和三个方向的转动，并且在轴箱的位置处施加垂向力，进行弹塑性接触计算。

2.2 车轮与辙叉弹塑性接触状态分析

通过固定辙叉不同位置处轮叉间接触斑形状和位置，可获得车轮通过辙叉的接触轨迹。接触轨迹可以直观地反映车轮通过辙叉的过程以及不同接触位置时的接触斑位置与大小。图8显示了标准货车LM型面车轮通过75 kg/m钢轨12号道岔固定辙叉的接触轨迹。

图8 车轮通过辙叉接触轨迹图Fig.8 The track chart when wheel passing the frog

从图8中可以看出，在车轮通过固定辙叉过程中，车轮首先与翼轨接触，随着车轮的前进，之后与翼轨和心轨同时接触，此时翼轨和心轨同时承载，最后完全过渡到心轨上，由心轨单独承载。

车轮与翼轨和心轨同时接触时的接触斑如图9所示，心轨上接触斑位于心轨顶面中心线附近，其纵向长度为26 mm，横向宽度为3 mm，相对狭长；翼轨上接触斑位于翼轨顶面靠近心轨侧，接触斑形状类似矩形，沿纵向长度为19 mm，沿横向宽度为5 mm。

图9 接触斑图Fig.9 Contact patch map

2.3 等效应力分析

通过上述动力学计算可得出在不同速度下车轮从翼轨过渡到心轨的瞬间，过渡位置与理论尖端的距离如表2所示。

表2 过渡位置

从表2中可以看出，车轮侧向通过辙叉的过程中，随着速度的增加，从翼轨向心轨过渡的位置逐渐远离理论尖端。心轨逐渐加宽，更有利于心轨承载。当速度达到50 km/h后，过渡位置不变，在距离理论尖端460 mm处。

在不同速度下的过渡位置建立轮叉三维有限元接触模型，分别施加动载垂向力与静载轴重的作用，比较其最大等效应力，如图10所示。

图10 动载垂向力与静载轴重作用下的等效应力Fig.10 Equivalent stress under the effect of dynamic load and static load

从图10中可以看出，动载垂向力作用下的轮叉等效应力均大于静载轴重的作用。当货车运行速度为30、40 km/h时，动载垂向力和静载轴重作用下的最大等效应力相差很小，但均达到了1 400 MPa，远远超过了材料的屈服极限，车轮与辙叉进入了塑性变形阶段。当运行速度达到50、60 km/h时，在距离理论尖端460 mm处车轮从翼轨向心轨过渡，其在静载轴重作用下的最大等效应力为833 MPa；在动载垂向力的作用下，其最大等效应力均超过了1 200 MPa，比在静态轴重作用下高出44.3%、67.7%以上，因此当货车在50 km/h的时速侧向通过固定辙叉时应考虑动载垂向力的影响。

由于货车在不同速度下通过辙叉的过程中，其从翼轨过渡到心轨的位置逐渐远离理论尖端，心轨顶面逐渐变宽，其在静载轴重作用下最大等效应力逐渐变小。尽管随着运行速度的增加，垂向力不断增大(表1)，但是车轮与辙叉之间的最大等效应力并不与速度成正比，其还与轮叉的型面有关系。因此应综合考虑速度与固定辙叉型面的耦合关系。

3 结论

应用SIMPACK软件模拟C80货车在满载状态下侧向通过固定辙叉的过程，分析轮叉之间的磨耗功率和垂向力等的变化情况。将动载垂向力施加在轮叉接触模型中，进行弹塑性接触计算，通过以上计算分析得出以下结论。

(1)当货车速度为30、40 km/h时，其磨耗功率未超过780 N·m/s，当速度达到50 km/h，磨耗功率增大了8倍之多，速度提高到60 km/h时，磨耗功率值高达40 750 N·m/s。

(2)C80货车标准LM型面车轮侧向通过辙叉过程中，在从翼轨向心轨过渡的瞬时其滚动圆半径变化较大，均为5 mm。过渡的瞬时对心轨产生冲击，垂向作用力随着运行速度的提高而增大，较大的冲击力使得心轨剥离掉块严重。

(3)当货车侧向通过固定辙叉的速度不断提高时，其从翼轨向心轨的过渡位置逐渐远离理论尖端，这有利于心轨承载。而在速度达到50 km/h后，过渡位置为距离理论尖端460 mm不变。

(4)动载垂向力和静载轴重分别作用时，轮叉之间的最大等效应力均超过了材料的屈服极限；当速度达到50、60 km/h时，动载垂向力作用下的轮叉最大等效应力较静载轴重作用时分别增大了44.3%、67.7%。

(5)在不同速度下C80货车通过固定辙叉时的磨耗功率、过渡位置、动载垂向力荷静载轴重作用下的等效应力分析，建议严格控制货车侧向通过固定辙叉的速度在50 km/h以下。