基于有限元理论的小号码道岔转换分析

马晓川，王 平，张梦楠，徐井芒

(西南交通大学高速铁路线路工程教育部重点实验室，四川成都 610031)

转换力计算是进行道岔转换设计的基础计算。设计上要求采用最少的牵引点实现尖轨和可动心轨的转换，牵引点转换力要求小于转辙机的额定功率，尖轨最小轮缘槽宽度要满足最小轮缘槽宽度要求。随着我国高速道岔的迅速发展，国内18号、38号以及42号道岔的设计已臻于成熟，小号码道岔的转换设计则有待进一步研究分析。本文以10号道岔为例，运用有限元理论，建立尖轨和心轨的有限元模型，研究滑床板摩擦系数、扣件横向刚度以及夹异物对道岔转换的影响。

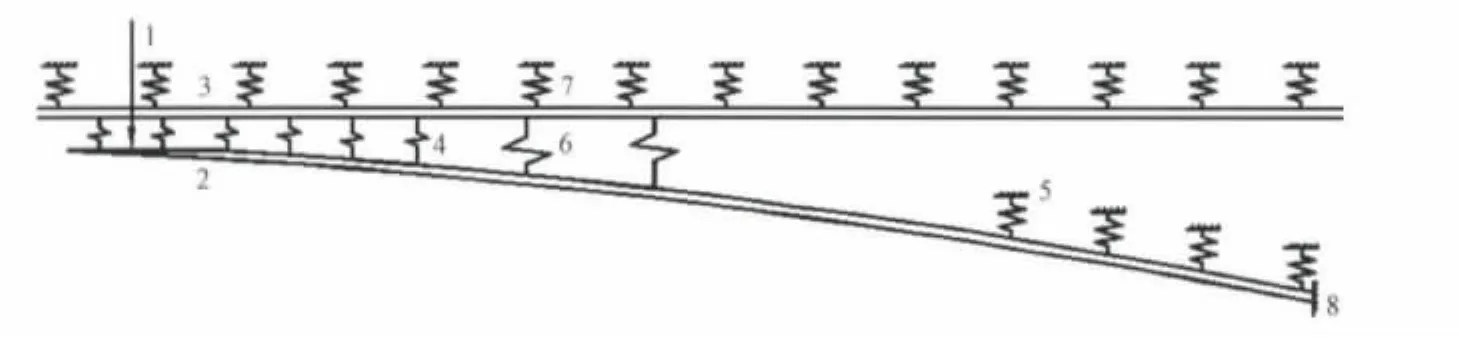
图1 尖轨转换的有限元模型

1 尖轨和心轨转换计算模型

1.1 尖轨转换计算模型

以10号道岔为例，尖轨活动段总长11.797 m，扳动到正位时的密贴段长5.941 m，扳动到反位时的密贴段长5.941 m，尖轨跟端类型为弹性可弯。采用单点牵引，牵引点距尖轨尖端 0.538 m，牵引动程0.160 m。牵引方式采用联动内锁闭。使用有限元软件建立尖轨转换的有限元模型，如图1所示。

1.2 心轨计算模型

以10号道岔为例，心轨活动段的长度7.89 m，扳动到正位时的密贴段长0.884 m，扳动到反位时的密贴段长0.906 m，心轨跟端类型为尖轨斜接头式单肢弹性可弯。采用单点牵引，牵引点距心轨尖端0.187 m，牵引动程0.107 8 m。牵引方式采用联动内锁闭。使用有限元软件建立心轨转换的有限元模型，如图2所示。

1.3 模型单元类型

使用有限元软件建立尖轨和心轨转换计算的有限元模型时，模型中使用的单元类型如下:

1)尖轨和心轨是截面线形变化的欧拉梁，只在水平面内发生横向变形，采用二维梁单元(beam3)模拟。

2)扣件在计算模型中起横向阻力的作用，采用非线性弹簧单元(combin39)模拟。

3)考虑到间隔铁受剪力和扭转力的作用，采用二维梁单元(beam3)模拟。限位器子母块贴靠前，限位器不受力，当限位器子母块贴靠后，限位器开始受力，因此采用非线性弹簧单元(combin39)模拟。

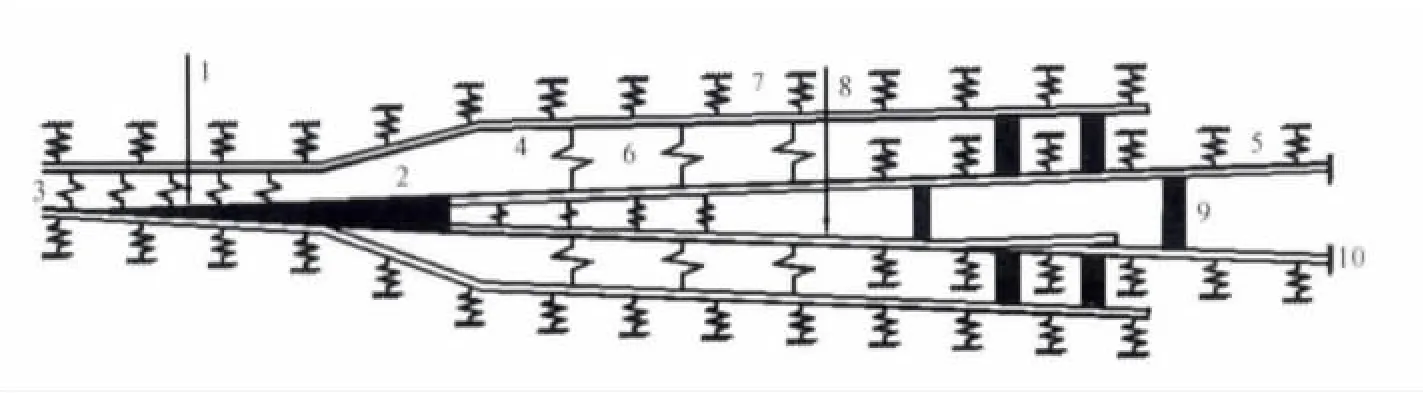
图2 心轨转换有限元模型

4)尖轨或心轨与基本轨未接触时，相互之间没有作用力，当尖轨或心轨与基本轨密贴后，尖轨或心轨受到较大的密贴力，因此密贴弹簧采用非线性弹簧单元(combin39)模拟。

5)尖轨或心轨与顶铁未接触时，尖轨或心轨不受顶铁力，尖轨或心轨与顶铁接触后受到顶铁力，因此顶铁采用非线性弹簧单元(combin39)模拟。

2 尖轨转换影响因素分析

2.1 滑床板摩擦系数对尖轨转换的影响

滑床板摩擦系数 μ 分别取 0，0.05，0.10，0.15，0.20，0.25和0.30时，尖轨转换力的变化趋势如图3所示，尖轨不足位移的变化趋势如图4(横坐标原点指尖轨尖端)所示。

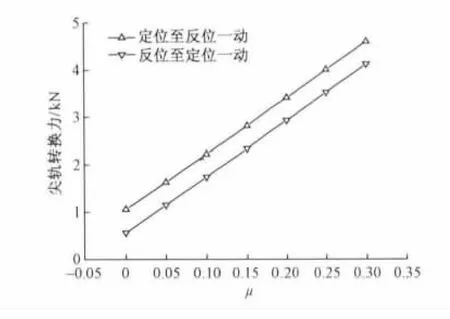
图3 尖轨转换力随滑床板摩擦系数变化趋势

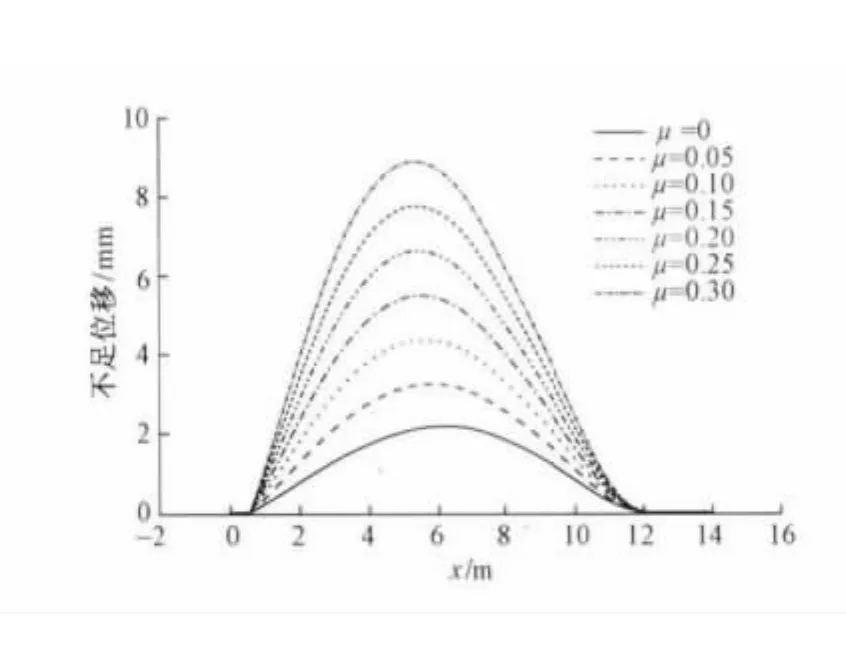
图4 尖轨不足位移随滑床板摩擦系数变化趋势

由图3和图4可见，牵引点的转换力随滑床板摩擦系数的增大而增大，不足位移随滑床板摩擦系数的增大而增大;滑床板摩擦系数取0.25时，最大转换力达到4 008.1 N，小于转辙机的额定功率6 000 N，能够满足要求。不足位移达到7.755 mm，不足位移值偏大，可以通过设置反变形降低不足位移。因此采取措施降低滑床板的摩擦系数，如滑床板涂油或设置辊轮，能够有效降低尖轨转换力和减小不足位移。

2.2 跟端扣件横向刚度对尖轨转换的影响

尖轨跟端扣件横向刚度 K分别取25，50，75和100 kN/mm时，尖轨转换力的变化趋势如图5所示，尖轨不足位移的变化趋势如图6所示。

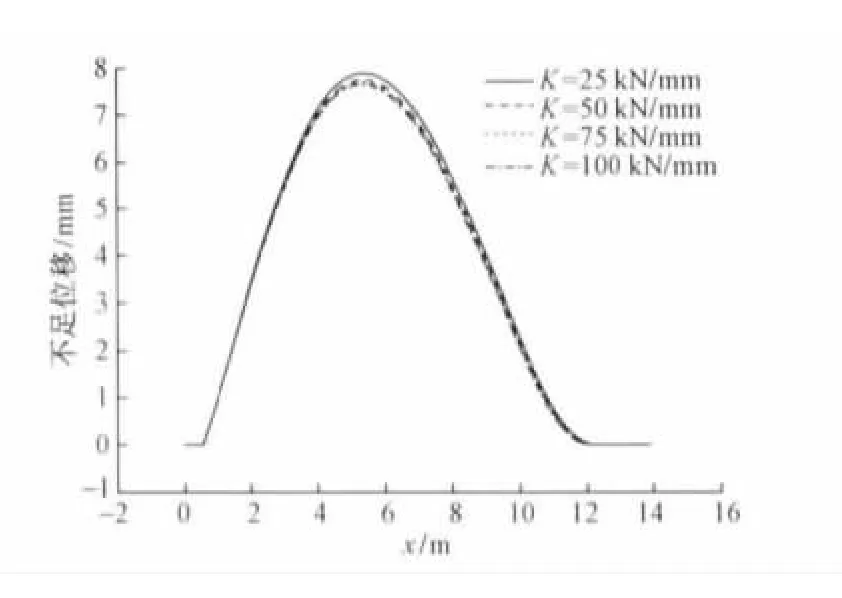
图6 尖轨不足位移随扣件横向刚度变化趋势

由图5和图6可见，尖轨转换力随扣件横向刚度的增大而略有减小，但变化幅度不明显;不足位移随扣件横向刚度的增大有所减小。因此，增大跟端扣件的横向刚度可以有效控制和减小尖轨的不足位移。同理，采取措施增大尖轨跟端横向刚度，如在尖轨跟端设置间隔铁，也能够有效控制和减小尖轨的转换力和不足位移。

2.3 夹异物对尖轨转换的影响

当牵引点处和牵引点后分别存在4，6和8 mm尺寸的夹异物，夹异物的位置分别是牵引点处、牵引点后1 m处、牵引点后2 m处和牵引点后3 m处时，牵引点的转换力变化如表1所示。＞6 000 N表示计算模型不收敛，扳动力远大于转辙机的额定功率6 000 N。

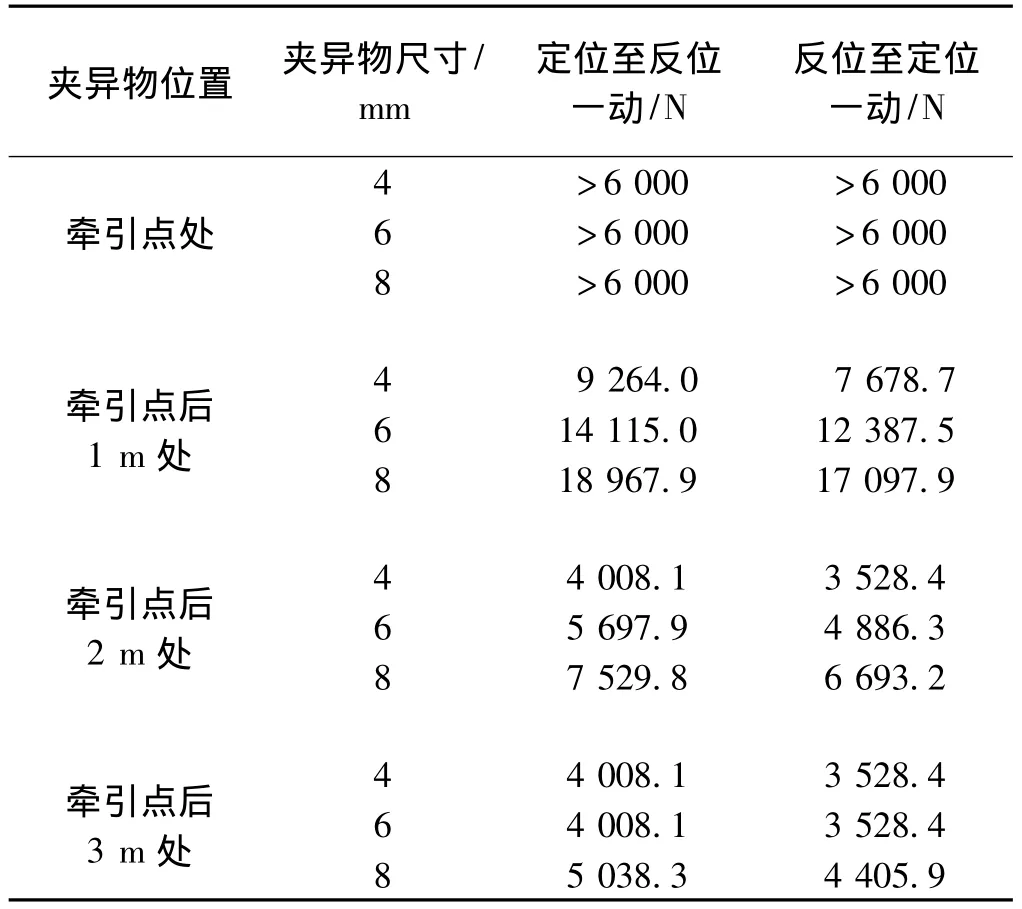
表1 夹异物对尖轨转换力的影响

由表1可见，夹异物的存在对于尖轨转换的影响很大，夹异物的尺寸越大，尖轨所需的转换力越大，夹异物位置距离牵引点越近，尖轨所需的转换力越大。牵引点后2 m处存在4和6 mm尺寸的夹异物以及牵引点后3 m处存在4，6和8 mm尺寸夹异物的情况，尖轨的扳动力满足要求(小于转辙机的额定功率6 000 N)，其他情况牵引点均会出现转换不到位的现象。因此在道岔转换时要定期清理异物，防止夹异物的存在造成尖轨转换不到位的现象。

3 心轨转换影响因素分析

3.1 滑床板摩擦系数影响

滑床板摩擦系数 μ 分别取 0，0.05，0.10，0.15，0.20，0.25和0.30时，心轨转换力的变化趋势如图7所示，心轨不足位移的变化趋势如图8(横坐标原点指心轨尖端)所示。

由图7和图8可见，心轨牵引点的转换力随滑床板摩擦系数的增大而增大，不足位移随滑床板摩擦系数的增大而增大。当滑床板摩擦系数取0.25时，心轨最大转换力是4 240.6 N，小于转辙机的额定功率6 000 N，满足设计要求。心轨不足位移是3.565 mm，不足位移值偏大可以通过设置反变形解决。采取措施降低滑床板的摩擦系数，如滑床板涂油或使用减磨滑床台，能够有效降低转换力，减小不足位移。

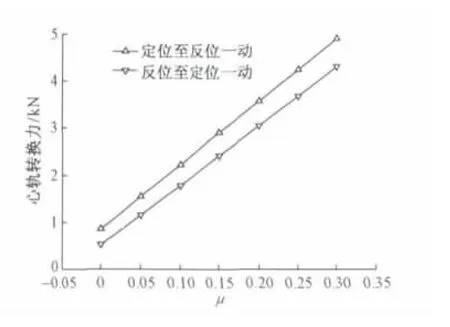
图7 心轨转换力随滑床板摩擦系数变化趋势

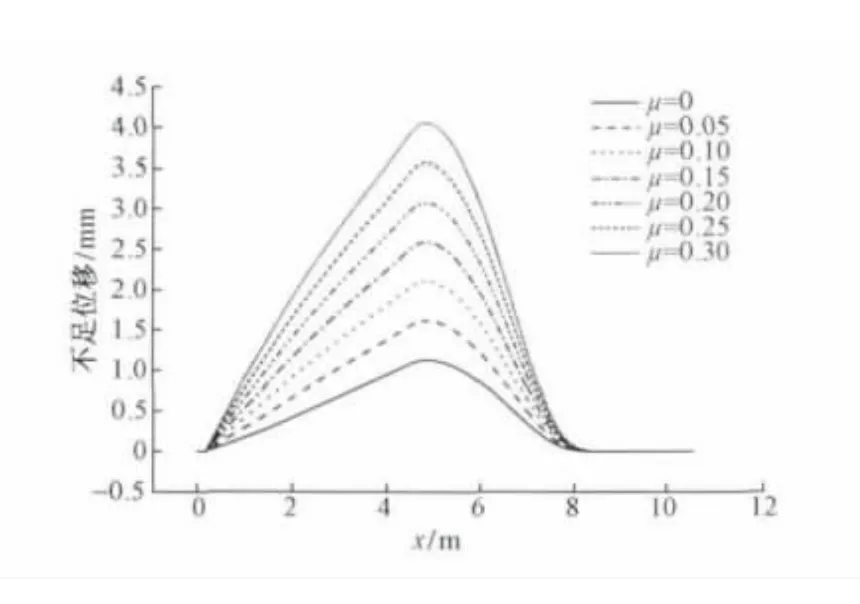
图8 心轨不足位移随滑床板摩擦系数变化趋势

3.2 跟端扣件横向刚度影响

心轨跟端扣件横向刚度 K分别取25，50，75和100 kN/mm时，心轨转换力的变化趋势如图9所示，心轨不足位移的变化趋势如图10所示。

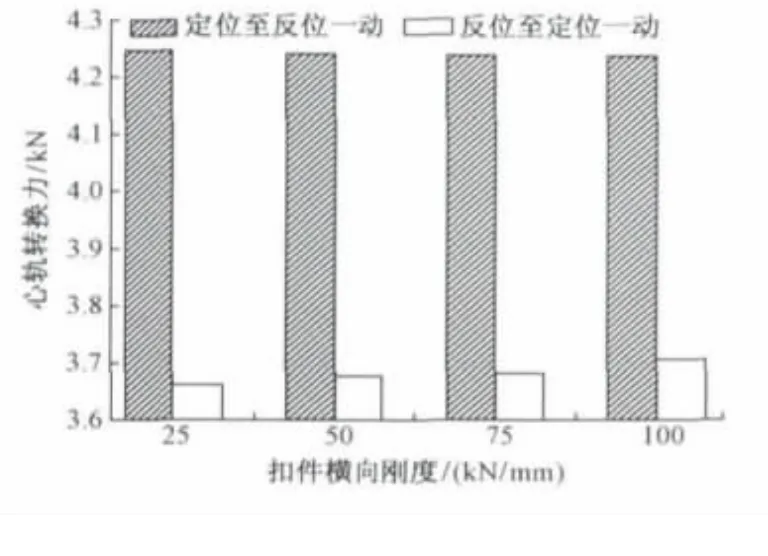
图9 心轨转换力随扣件横向刚度变化趋势

由图9和图10可见，定位至反位心轨转换力随扣件横向刚度的增大而减小，反位至定位心轨转换力随扣件横向刚度的增大有小幅度的上升，不足位移随扣件横向刚度的增大而减小，考虑到定位至反位转换力高于反位至定位转换力，因此，增大扣件横向刚度可以有效地减小心轨转换力和降低心轨不足位移。同理，采取措施增加心轨跟端横向刚度，如在心轨跟端设置间隔铁，可以有效控制心轨的转换力和降低不足位移。

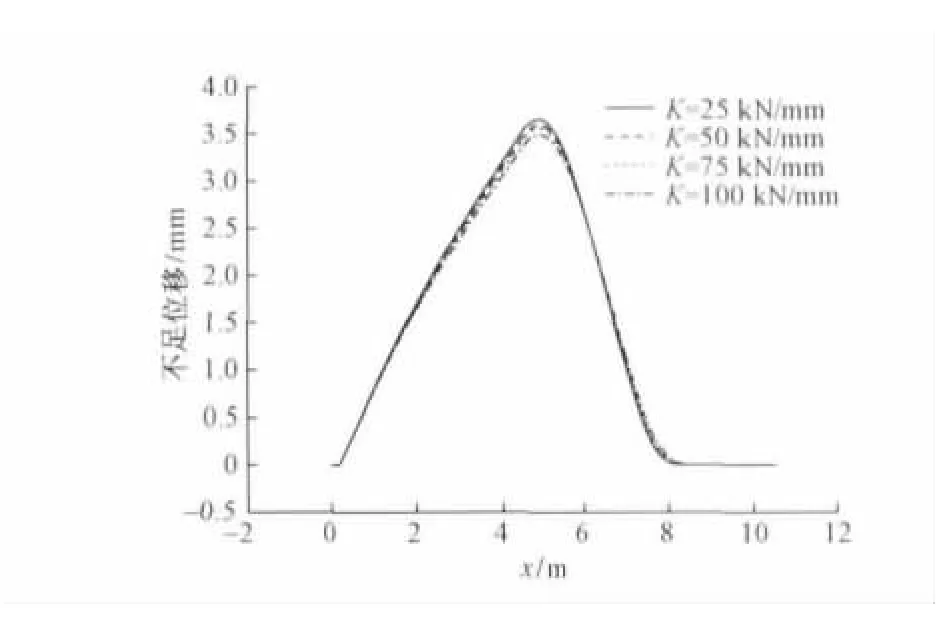
图10 心轨不足位移随扣件横向刚度变化趋势

3.3 夹异物尺寸影响

当牵引点处和牵引点后分别存在4，6和8 mm尺寸的夹异物，夹异物的位置分别是牵引点处、牵引点后1 m处、牵引点后2 m处和牵引点后3 m处时，心轨牵引点的转换力变化如表2所示。＞6 000 N表示计算模型不收敛，扳动力远大于转辙机的额定功率6 000 N。

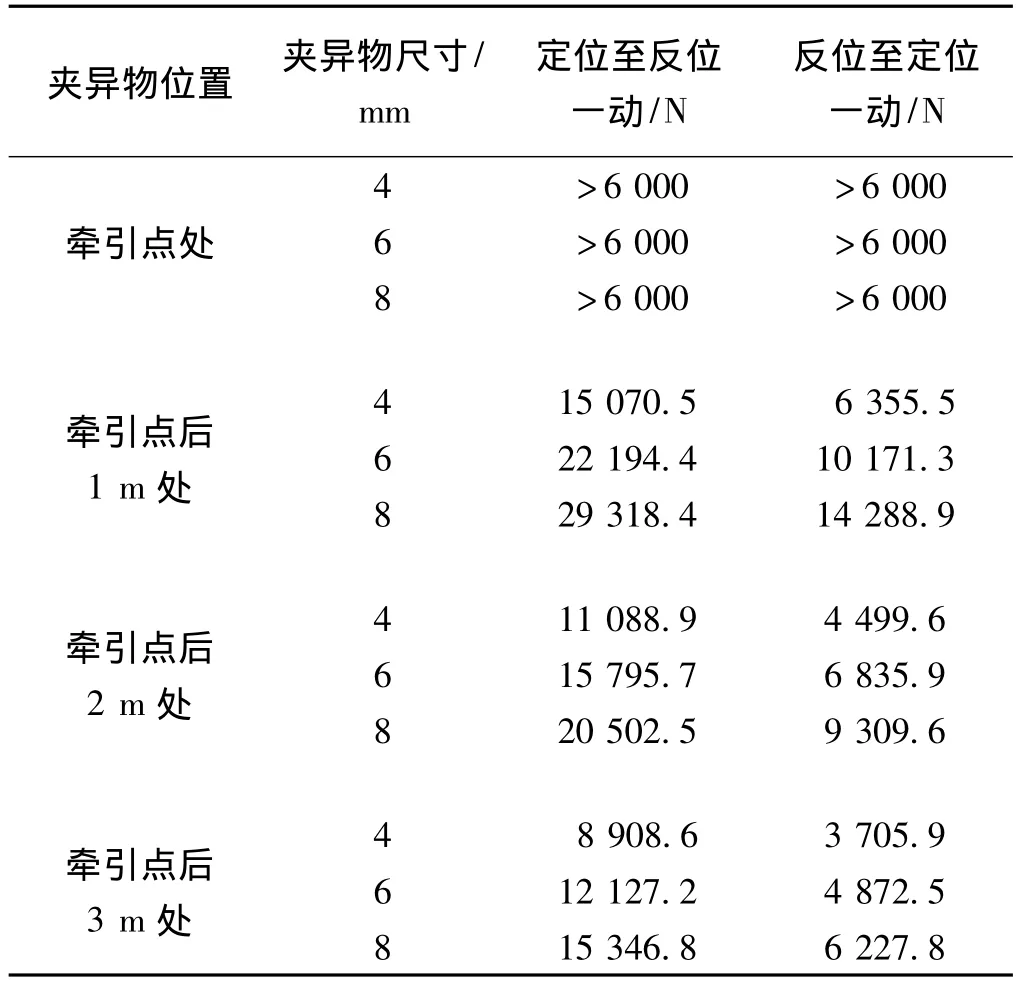
表2 夹异物对心轨转换力的影响

由表2可见，夹异物的存在对心轨转换有很大的影响，夹异物尺寸越大，心轨所需转换力越大，夹异物距离牵引点越近，心轨所需转换力越大。表中列出存在夹异物的12种情况，定位至反位牵引点的转换力均＞6 000 N，心轨均不能转换到位。因此，道岔需定期清理异物，以防止夹异物的存在导致心轨转换不到位的现象。

4 结论和建议

本文以10号道岔为例，使用有限元的方法，分别建立了尖轨和心轨的转换计算模型，分析了滑床板摩擦系数、扣件横向刚度和夹异物对道岔转换的影响，得出以下3点结论和建议。

1)尖轨和心轨的转换力均随滑床板摩擦系数的增大而增大，不足位移随滑床板摩擦系数的增大而增大，为满足设计要求，可以采取有效措施减小滑床板的摩擦系数，如设置辊轮、涂油、定期清理滑床板和使用减摩滑床台等措施。

2)随着尖轨和心轨跟端扣件横向刚度的增大，尖轨和心轨的转换力随之减小，不足位移也随之减小，因此通过增大扣件横向刚度的措施可以有效减小尖轨和心轨的转换力和不足位移。同时，采取措施增加尖轨和心轨跟端横向刚度，如在跟端设置间隔铁，可以有效控制和减小转换力和不足位移。

3)夹异物的存在对尖轨和心轨的转换影响非常大，特别是夹异物出现在尖轨或心轨牵引点附近时，将会直接导致尖轨或心轨转换不到位，严重时影响行车安全，因此定期清理道岔中出现的夹异物是十分有必要的。

［1］王平．高速铁路道岔设计理论与实践［M］．成都:西南交通大学出版社，2011．

［2］蔡小培．高速道岔尖轨与心轨转换及控制研究［D］．成都:西南交通大学，2008．

［3］沈长耀，王明治，蒋慧娟．弹性可弯尖轨扳动力计算［J］．铁道标准设计，1991(4):1-13．

［4］刘语冰．弹性可弯尖轨双牵引点的扳动力计算［J］．铁道标准设计，1993(1):12-18．

［5］蔡小培，李成辉．高速道岔心轨扳动力和不足位移控制研究［J］．铁道学报，2008(4):48-51．

［6］蔡小培，李成辉，王平．滑床板摩擦力对尖轨不足位移的影响［J］．中国铁道科学，2007(1):8-12．

［7］何乐平，李成辉．滑床台摩擦系数对双肢弹性可弯心轨扳动力及不足位移影响的计算分析［J］．铁道建筑，2006(6):88-90．

［8］李向国，鲍怀义，岳渠德．提速道岔转换力计算机模拟研究［J］．石家庄铁道学院学报，2002，15(3):53-55．

［9］井国庆，李成辉．18号可动心轨道岔不足位移的ANSYS仿真分析［J］．铁道建筑，2007(4):108-110．