对2020年高考北京卷第20题的拓展*

江苏省大港中等专业学校(222047) 陈 杰

江苏省太湖高级中学(214125) 翟洪亮

圆锥曲线中的定点、定值问题是高考的热点和难点,而且时考时新.笔者通过对2020年高考北京卷第20 题进行探讨,发现其图形内部蕴涵两条性质,并将它们推广到一般情形及其他圆锥曲线.现整理成文,与大家交流.

一、试题呈现

已知椭圆C:=1(a ＞b ＞0)过点A(-2,-1),且a=2b.

(Ⅰ)求椭圆C的方程;

(Ⅱ)过点B(-4,0)的直线l交椭圆C于M,N两点,直线MA,NA分别交直线x=-4 于点P,Q.求的值.

二、参考答案

解(Ⅰ)由题设得= 1,a= 2b, 解得a2= 8,b2=2,所以椭圆C的方程为=1.

(Ⅱ)设M(x1,y1),N(x2,y2), 直线MN的方程为y=k(x+ 4), 代入= 1 得(4k2+ 1)x2+ 32k2x+(64k2-8)= 0.由根与系数关系得x1+x2=x1x2=.直线MA的方程为y+1=(x+2),令x=-4, 得yP=.同理可得,yQ=

显然,yP yQ ＜0,且所以

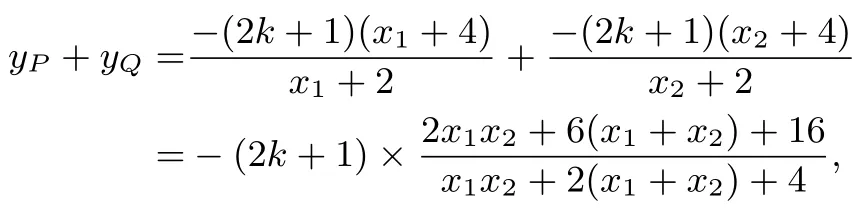
而

三、试题拓展

本题考查直线与椭圆的位置关系, 试题运算量大, 区分度明显, 注重对数学运算素养的考查.做完此题, 笔者连结AB, 如图1, 计算直线AM、直线AN、直线AB斜率,经过探究发现:

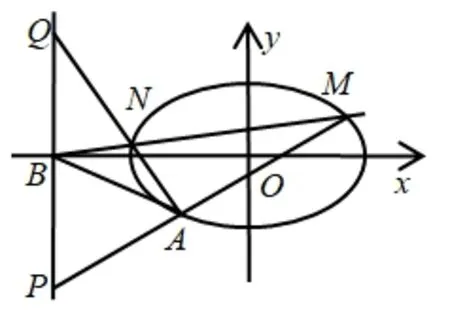
图1

变式1已知椭圆= 1, 点A(-2,-1),若过点B(-4,0)的直线l交椭圆C于M,N两点, 则kAM+kAN=2kAB.

证明设M(x1,y1),N(x2,y2), 直线MN的方程为y=k(x+ 4), 代入= 1 得, Δ = (32k2)2-4(4k2+1)(64k2-8)＞0,由根与系数关系得x1+x2=

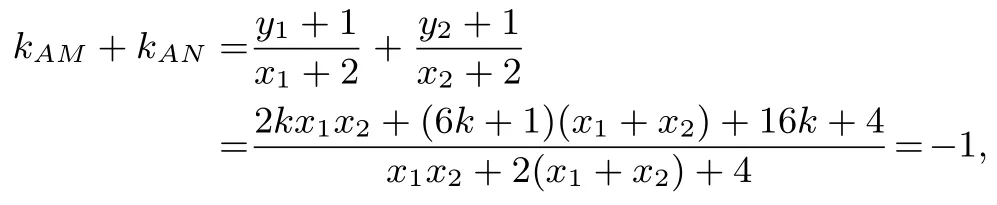
kAB=所以kAM+kAN=2kAB.

思考命题人为什么要取椭圆上的点A(-2,-1)? 这与所给椭圆=1 和直线x=-4 之间有何关系呢? 经过探究发现,xAxB=a2=8,猜想试题结论可推广到椭圆的一般情形.

性质1已知椭圆C:= 1(a ＞b ＞0)过点A(x0,y0), 若过点的直线l交椭圆C于M,N两点, 直线AM,AN分别交直线x=于点P,Q, 则:(1)kAM+kAN=2kAB;(2)|BP|=|BQ|.

证明设M(x1,y1),N(x2,y2), 直线MN的方程为y=k(x -), 代入= 1 得(a2k2+b2)x2-由根与系数关系得x1+x2=

(1)因为kAB=所以

所以kAM+kAN=2kAB.

(2)直线AM的方程为y - y0=令x=得yP=+y0.同理可得,yQ=+y0.显然,yP yQ ＜0, 且yP+yQ=+ 2y0, 由(1)知所以yP+yQ=×+2y0=0,所以|BP|=|BQ|.

圆锥曲线是由平面截圆锥而得.用一个不垂直于圆锥的轴的平面截圆锥,当截面与圆锥的轴夹角不同时,可以得到椭圆、双曲线、抛物线,我们通常把椭圆、双曲线、抛物线统称为圆锥曲线.既然椭圆、双曲线、抛物线都是由圆锥被平面所截,那么它们往往具有类似的性质.经过探究,发现上述性质也可推广到双曲线.

性质2已知双曲线C:=1(a ＞0,b ＞0)过点A(x0,y0),若过点的直线l交双曲线C于M,N两点, 直线AM,AN分别交直线x=于点P,Q, 则:(1)kAM+kAN=2kAB;(2)|BP|=|BQ|.

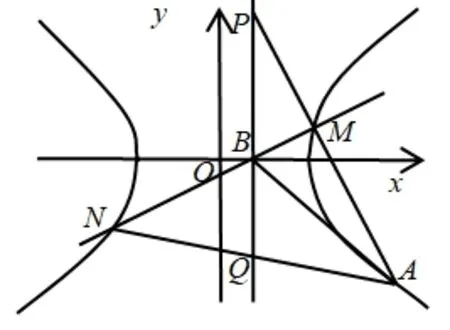
图2

证明设M(x1,y1),N(x2,y2), 直线MN的方程为= 1 得(a2k2- b2)x2-+a2b2= 0.由根与系数关系得x1+x2=,x1x2=

(1)因为kAB=所以

所以kAM+kAN=2kAB.

(2)直线AM的方程为y - y0=(x - x0),令x=得+y0.同理可得,yQ=+y0.显然,yP yQ ＜0, 且yP+yQ=+ 2y0, 由(1)知所以yP+yQ=+2y0=0,所以|BP|=|BQ|.

上述性质能否推广到抛物线呢? 若能推广,定点坐标又是什么呢? 经过探究可得:

性质3如图3, 已知抛物线C:y2= 2px(p ＞0)过点A(x0,y0),若过点B(-x0,0)的直线l交抛物线C于M,N两点, 直线AM,AN分别交直线x=-x0于点P,Q, 则:(1)kAM+kAN= 2kAB; (2)|BP|=|BQ|.

图3

性质3 的证明思路与性质1 和性质2 的证明相仿,不再赘述.