重视概念定义研习，突出基本方法训练

谢广喜

一、基本考点概述

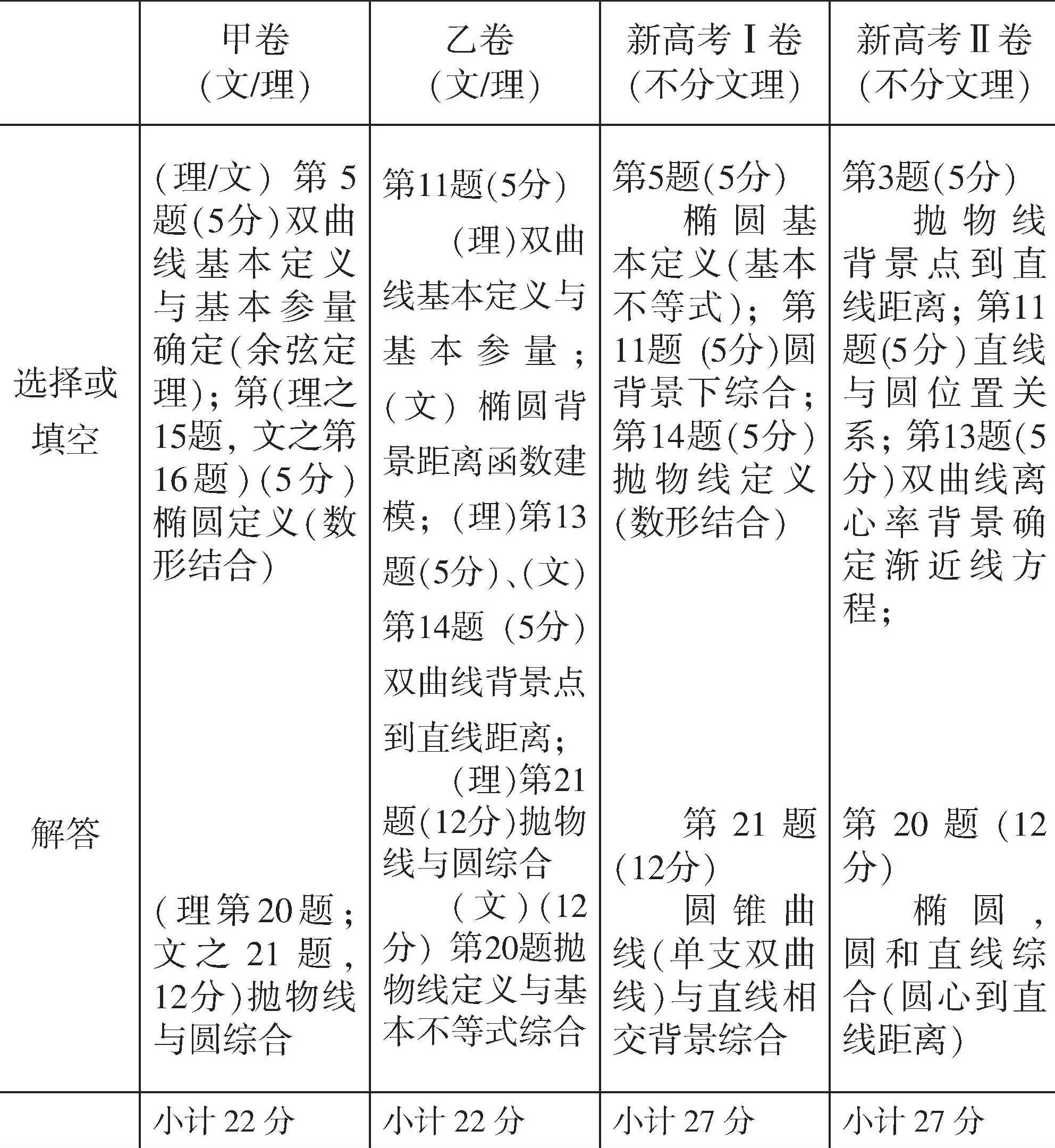
根据多年来特别是近几年我们对高考数学试题研究的基本经验，尤其是在总结了今年六份全国卷试题之后，我们分析了其中的平面解析几何方面命题的主要考点，希望能为2022届高三毕业生复习备考有关知识内容提供一个原则性、方向性的指导. 我们将有关主要命题要点具体分析总结如下：

结合上表，我们容易看出，总体来说，平面解析几何有关试题在高考全国数学卷试题中占分约22-27分左右（满分150分），占比约15%，难度也不算大，基本上是以1-2道选择题、1道填空题和1道解答题为主（解答题主要出现在倒数第二道，该位置决定了其难度较大，但第（1）问还是基础题，以送分为主，第（2）问也是以典型基础知识、基本技能考查为主，不过解题过程通常比较繁），考点分布主要涉及：点到直线距离公式的应用（这个点可以是平面内给定一点（特别地，如：这个点还可以是圆锥曲线的焦点，圆的圆心等等），也可以是平面上的动点，比如是直线上一动点、圆周上一动点、圆锥曲线上一动点等等，尤其是双动点距离问题，如果其中一个点在圆上，经常会将该动点先转化为圆心，变为定点，最后在再转化回去），当然，提到距离，就不能不提圆锥曲线（椭圆、双曲线、抛物线和圆）定义（很多客观题的解题切入点），圆锥曲线背景的有关参量以及标准方程的确定等等;也可能会和平面向量基本概念、简单的三角最值问题、一元二次方程根与系数关系、基本不等式等等知识产生横向的联系;在数学思想方法上，主要表现为化归与转化思想（函数与方程之间的转化，参数换元，第一定义与第二定义间转化等等）以及数形结合思想（以形助数），偶尔也会分类讨论等等. 考生要特別注意挖掘图形中蕴含的不变量或几何对称性、关系对称性等，因为它们往往可能是问题迅速解决的关键突破点.

因此，对于2022新一届考生的复习备考，关于平面解析几何部分，我们的建议是：①全面复习（包括比如今年没考到的而往年经常涉及的圆锥曲线“三定”问题（定值、直线过定点，动点在定制直线上）），复习第一阶段一定要指导再次有计划地认真阅读教材，也许可能会有和初学时不一样的感悟;②重点掌握，特别是我们上面提到的一些典型的问题及其处置办法，复习过程中要特别重视有关概念、定义研究与再学习（比如一个定义附加的条件有什么作用，如果去掉会怎么样，典型的情况比如椭圆定义中的要求）;③ 突出基本解题方法的训练，注重解题工作结束的反思（特别是做错的时候，搞明白错因以后才不容易再犯类似的错误），在此基础上落实课标“四基”要求.

二、平面解析几何典型问题预测例析

预测考点1：以单一选择题形式，考查圆锥曲线背景下距离量的确定或某种距离函数的最值.

【评注】通过巧妙转化，变双动点问题为单动动点（这是很重要的一点）问题. 当然，将距离函数表达为某个变量的二次函数的形式往往是有条件的，比如题中的P点坐标就有一定的特殊性（对于标准圆锥曲线而言，定点通常在坐标轴上），同时，由于动点在给定圆锥曲线上，所以其坐标往往只在一定的范围内取值，也就是说，这时得到的二次函数往往只在局部区间上有定义. 另外，有时可先表出距离函数的平方的形式（由于d≥0，所以它是距离函数的等价形式），讨论及表达起来较方便.

预测考点2：以圆锥曲线的第一、第二定义为背景的选择题或填空题，能否联想到有关定义，甚至能否在第一、第二定义之间快速转化，这往往成为破题的关键

【评注】2021年新高考全国Ⅰ卷第5题就是以椭圆第一定义为切入点（配合基本不等式立得最后答案）;第21题之第（1）小题也是双曲线的第一定义（仅有右支），二者都是以圆锥曲线定义为命题背景的，当然，破题的要害也是从圆锥曲线定义出发的.

【联想】（2020年高考全国Ⅰ卷理第4题）已知A为抛物线C∶y2=2px（p>0）上一点，点A到C的焦点距离为12，到y轴的距离为9，则p=（  ）

A. 2    B. 3    C. 6    D. 9

预测考点3：无论是几何对称还是关系对称，它们二者都是可以帮助我们简化思维过程记具体解题的书写过程的重要途径.

很多读者对几何对称比较熟悉，典型的中心对称或轴对称都是我们十分清楚的几何对称，所谓关系对称是指在同一个大命题下，其中的两个具体条件或结论具有简单的置换性，这样我们在求出和其中一部分条件密切相关的结论后，将其中的关键变量简单置换，即可得到和另一个条件密切相关的和前一个结论相当类似的结论，这样我们就可简化思维，也简化了答案的书写长度.

例3.（2017年高考全国Ⅰ卷理第10题）已知F为抛物线C∶y2=4x的焦点，过F做两条互相垂直的直线l1，l2，直线l1与C交于A，B两点，直线l2与C交于D，E两点，则AB+DE的最小值为（   ）

【评注】一方面，我们通过挖掘隐含的平面几何关系，使隐蔽的解题核心关键量凸显，简化解题过程;另一方面（更主要的），通过巧妙代换，迅速地由P点的坐标得到Q点的坐标. 发现点Q与点P关于原点对称是非常关键的一步！因为这一关系的发现，使得？驻APQ的面积的表示变得异常简单了，随后的基本不等式的应用就没有什么实质性的困难了，当然，注意k的取值范围以及取等号条件仍是我们最后需关注的细节！

预测考点4：以数学文化为背景的圆锥曲线问题，比如阿波罗尼圆、阿基米德三角形等等.

【评注】联想到阿波罗尼圆的定义是我们能否快速解决本题的关键突破口.

预测考点5： 圆锥曲线背景下的三定问题（定值探求与证明、动直线过定点、动点在定直线上），比如定值探求，通常是先直觉、后逻辑，也即是先用特殊情形探路（为一般情形指明方向），再针对一般情况推理论证.

例6.（2011年高考四川卷理第21题）椭圆上有两点A（-1，0），B（1，0），过其焦点F（0，1）的直线l与椭圆交于C，D两点，并与x轴交于点P，直线AC与直线BD交于点Q，

【评注】本题的第（2）问参考答案解法采用平方法，虽然此法实现了表达式的对称性（关于x1，x2）转化，但此法涉及开方后符号的判定，过程比较繁琐，以上解法则充分利用椭圆方程进行恒等变换，不用平方就实现表达式的对称性转化，从而仅涉及x的一次表达式，自然，由开方导致的符号判断问题也自动消失了，所以，如此一来，处理过程比原解法简化了许多.

下面再举一例证明 动直线过定点的问题.

【评注】上面的解法也许不是最尖简单的，但却是最容易想到的思路，一个问题的解决往往是从最容易想到的办法试探，得到结果后再想着如何简化、如何有更简单便捷的思路？留给读者思考，这里就不多说了.

【同步练习】

【同步练习参考答案与评注】