珠子绕空心圆环的动力学过程研究

蓝应莲 杨柳 李文博 高婧 吴世宝

摘 要：本文对“珠子动力学”问题进行探究，建立了小球运动过程理论模型，基于点的合成运动、动量矩守恒和动能定理，推导速度和加速度的变化规律，并结合数值模拟分析相关参数对速度和加速度变化趋势的影响。数值分析结果表明，圆环的半径对小球运动的速度影响较大，对加速度影响较小;小球的直径对小球运动的速度和加速度几乎没有影响。

关键词：点的合成运动;动量矩守恒;动能定理;数值模拟

中图分类号：O313.7  文献标识码：A  文章编号：1673-260X（2021）12-0005-05

动力学问题一直以来都是理论力学问题的一个重要分支，在许多工程领域都有非常广泛的应用，这其中也包含许多经典的动力学问题，“珠子動力学”[1]便是其中之一。所谓“珠子动力学”，指的是让一个圆环绕着垂直于其直径的轴旋转，在圆环内放置一个小球，当圆环旋转时，探究圆环内小球的相关动力学参数与相关因素的影响。这一现象的核心在于让圆环绕着垂直于直径的轴旋转，并研究此过程中圆环内小球的运动可能受哪些因素影响[2]。本文对“珠子动力学”所阐述的现象进行了理论分析和数值模拟。

1 理论模型

1.1 模型假设

通过对“珠子动力学”背景的分析，对圆环的形状、圆环在空间中的放置方式和旋转方式、小球的动力学过程有如下解释：

（1）关于圆环的形状。假定涉及的圆环是指具有一定大小内径和壁厚的空心圆管，该圆管的内径与要放置进去的小球的外径大小相同，且可以使小球在圆环中自由地运动。

（2）关于圆环在空间中的放置方式和旋转方式。假定涉及的圆环均放置在竖直平面内，且圆环绕着竖直轴进行逆时针旋转。

（3）关于小球的动力学过程。由于小球在圆环内部的运动过程属于多个阶段运动，较为复杂，在研究时可以先选择其中较为典型的运动过程进行研究。因而，假定小球在初始时刻放置在圆环最高点，受到微小扰动后向圆环最低点运动，只研究小球从圆环最高点运动到最低点这一动力学过程中的相关问题。

（4）关于小球的动力学参数。动力学问题主要反映在物体的速度和加速度变化规律中，因而主要研究小球在上述动力学过程中速度和加速度的变化规律。

1.2 模型建立

如图1所示，将某个半径为R的光滑圆环放置在竖直平面内，且可以绕着竖直轴旋转。在初始时刻，某个直径为d的钢球位于圆环的最高点，此时圆环正在绕着竖直转轴逆时针旋转，其角速度为ω。在其后某一时刻，位于最高点的钢球受到微小的扰动而离开最高点，开始向圆环的最低点运动。此时钢球球心与圆环圆心的连线与竖直转轴之间的夹角为θ，圆环绕竖直转轴逆时针旋转的角速度为ω1。

接下来对钢球在向下运动过程中某一时刻的速度进行分析。取钢球为动点，运动系统与圆环固定相连，则由运动的合成，得

va=ve+vr  （1）

其中，va是绝对速度，也是钢球相对于静参考系运动的速度，其大小和方向都未知;ve是牵连速度，是圆环上与钢球重合的那一点相对于静参考系的运动速度。显然，圆环上与钢球重合那一点此时正在绕着点O1做逆时针方向的定轴转动，其大小为

式（18）就是钢球从圆环最高点向最低点运动过程中加速度的变化规律。由式（16）和式（18）可知，影响钢球从圆环最高点向最低点运动过程中速度和加速度变化趋势的因素为钢球的质量m、圆环的半径R以及圆环对竖直轴的转动惯量J。进一步分析可知，钢球质量m的变化主要是依靠钢球直径d的变化来实现的，而不论是改变钢球的直径d还是圆环的半径R，最终都会引起圆环对竖直轴的转动惯量J的变化[3]，所以，影响钢球从圆环最高点向最低点运动过程中速度和加速度变化趋势的主要因素为钢球的直径d和圆环的半径R。

2 数值模拟

2.1 速度和加速度的变化规律

由上述理论模型，得到了钢球从圆环最高点向最低点运动过程中速度和加速度随钢球球心与圆环圆心的连线和竖直转轴之间的夹角θ的函数关系式。由于θ也是随时间t变化的函数，所示钢球的速度和加速度随夹角θ变化的函数关系式也可以看作是随时间t变化的函数关系式[4]。因而，通过绘制钢球的速度和加速度随夹角θ的变化图像，可以大致观察出钢球在从圆环最高点向最低点运动过程中其速度和加速度的变化趋势。

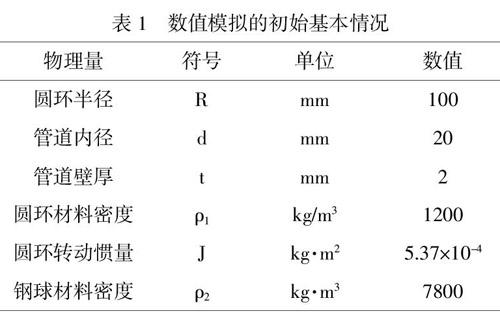
在进行数值模拟时，首先对系统的基本条件进行了规定。所模拟的系统的基本情况如表1所示。

由表1可知，圆环是塑料材质，其密度为1.2×103kg/m3，其半径为100mm，壁厚为2mm，其管道内径和钢球的直径均为20mm。由于圆环的形状较为复杂，其转动惯量J不便于利用积分法进行计算，因而选择在CATIA软件中按表1所示的尺寸绘制该圆环的三维数模，并在CATIA软件中利用其测量模块测得其绕竖直轴转动时的转动惯量[5]。在CATIA软件中绘制的三维数模和测量模块如图2所示。

由图2可知，在绘制该圆环的三维数模时，选择在yz平面绘制了圆环的截面草图，并利用旋转体功能生成了该圆环的三维数模[6]。此外，由图2右侧的对话框可知，题目中的竖直轴相当于CATIA软件中的x轴或y轴，在修改材料的密度[5]后，CATIA软件将自动计算出该数模对3个坐标轴的转动惯量，只需要该数模对x轴或y轴的转动惯量即可。

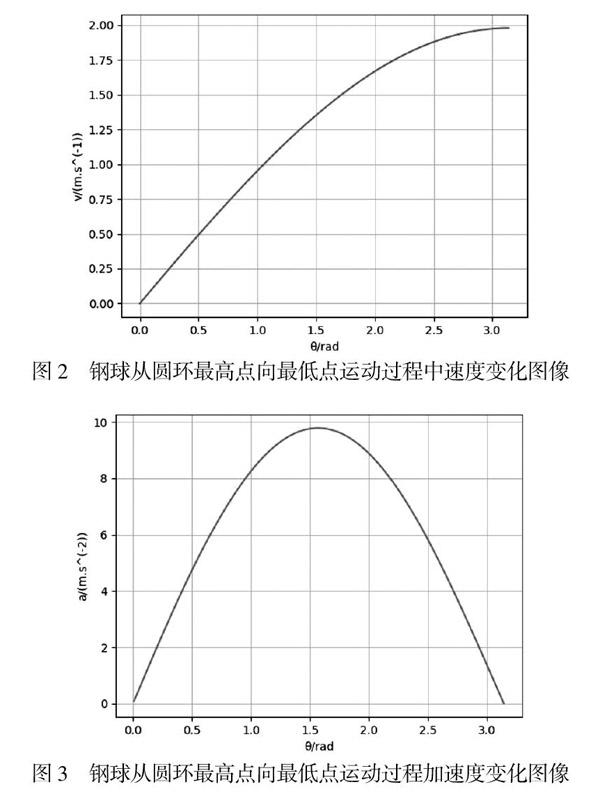
在获得圆环的转动惯量后，利用Python语言编程，对钢球从圆环最高点向最低点运动过程中其速度和加速度的变化图像进行了数值模拟，其结果分别如图2和图3所示。

由图2和图3可知，钢球从圆环最高点向最低点运动的过程中，其速度逐渐增加，并在θ=π时达到最大值;但加速度先是从0开始增加到最大值随后再次减小为0，并在θ=π/2时取得最大值。因而，钢球从圆环最高点向最低点的运动是一个加速度先增大后减小的加速运动。

2.2 圆环半径对速度和加速度变化趋势的影响

在模拟圆环半径对钢球的速度和加速度变化趋势的影响时，首先需要获得在钢球直径不变的情况下，不同半径的圆环对应的转动惯量。随后，将编写好的Python程序中的半径和转动惯量修改为要探究的半径及其对应的转动惯量[7]，就可以得到不同的圆环半径对应的钢球速度和加速度变化图像。

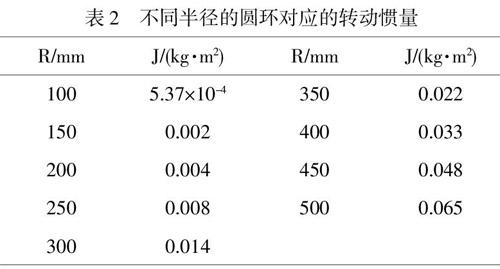
在计算不同半径的圆环对应的转动惯量时，利用了CATIA软件进行设计，在保证钢球直径为20mm的情况下，获得了几种不同半径的圆环对应的转动惯量，如表2所示。

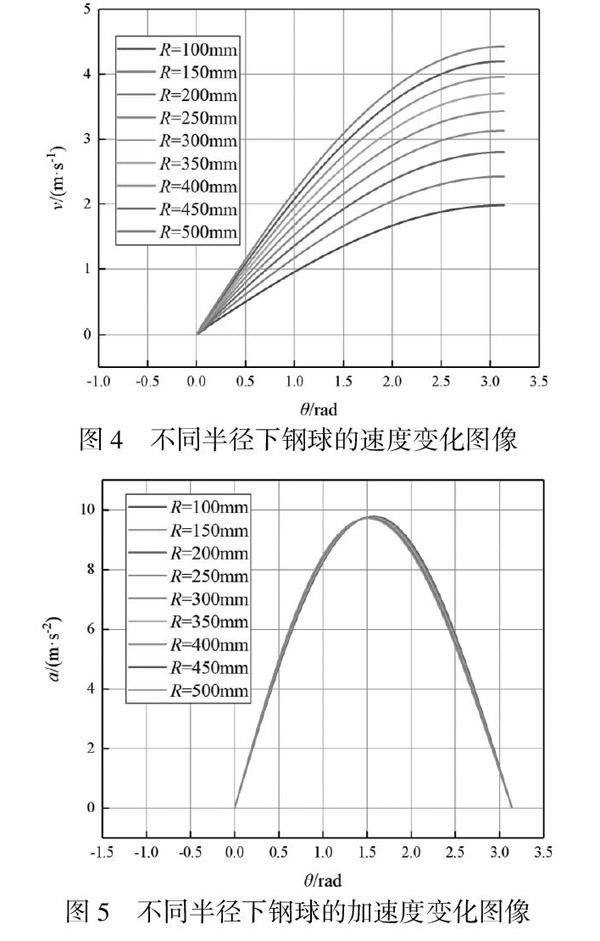
由表2可知，随着圆环半径的增加，圆环的转动惯量也有较为明显的增加。按表2所示的数据对Python程序進行修改，运行程序后模拟出的不同半径下钢球的速度和加速度变化图像分别如图5和图6所示。

由图4可知，随着圆环半径的增加，钢球在通过圆环同一位置时的速度都处于增加的趋势，且钢球的最大速度的增加幅度最大，说明圆环的半径对钢球运动速度的变化趋势有较大的影响，且随着圆环半径的增大，钢球在通过圆环同一位置时的速度均增大。由图5可知，随着圆环半径的增加，钢球的加速度变化图像的变化非常小，说明圆环半径的变化不会使得钢球运动过程中加速度的趋势发生显著的变化。

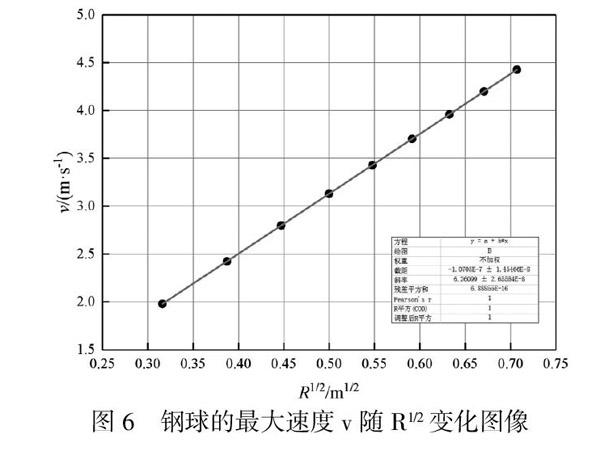
为判断钢球的最大速度和圆环的半径是否存在定量关系，利用图6所示的数据，绘制了钢球的最大速度v随R1/2的变化图像，并进行了直线拟合，如图6所示。

由图6可知，钢球的最大速度v和R1/2呈现出较高的正比关系，且该直线的斜率为6.26099，这个数值恰好与2g1/2相等，说明钢球的最大速度和圆环半径R的1/2次方成正比。

2.3 钢球直径速度和加速度变化趋势的影响

在模拟钢球直径对钢球的速度和加速度变化趋势的影响时，首先需要获得在圆环半径不变的情况下，不同钢球直径的圆环对应的转动惯量[8]。随后，将编写好的Python程序中的钢球直径和转动惯量修改为要探究的球径及其对应的转动惯量，就可以得到不同的钢球直径对应的钢球速度和加速度变化图像。

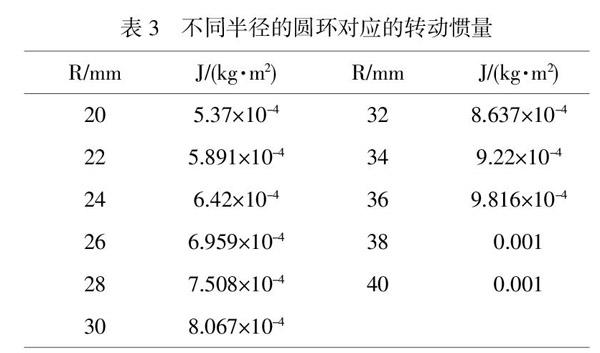
在计算不同钢球直径的圆环对应的转动惯量时，再次利用了CATIA软件进行设计，在保证圆环半径为100mm的情况下，获得了几种不同钢球直径的圆环对应的转动惯量，如表3所示。

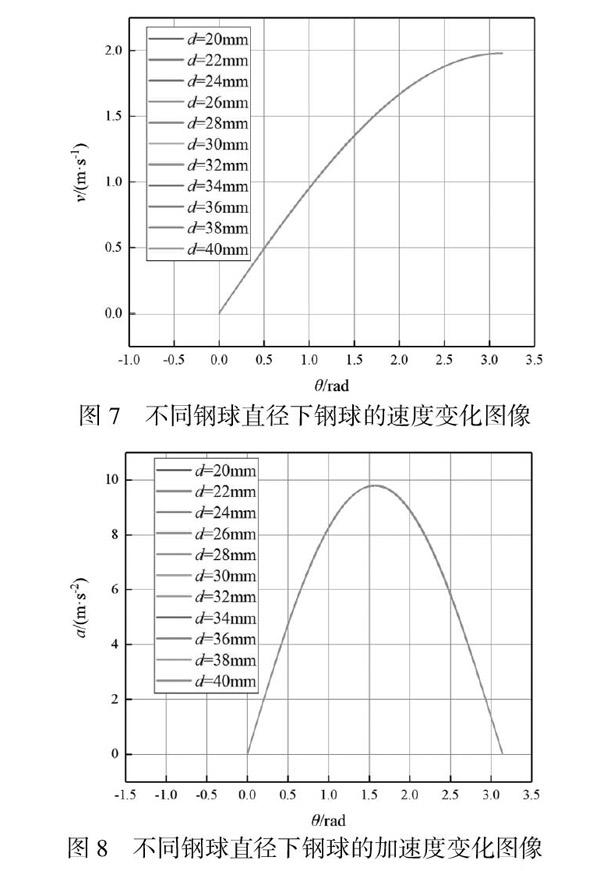
由表3可知，随着钢球直径的增加，圆环的转动惯量的增加幅度并不明显。按表3所示的数据对Python程序进行修改，运行程序后模拟出的不同钢球直径下钢球的速度和加速度变化图像分别如图7和图8所示。

由图7和图8可知，随着钢球直径的增加，钢球的速度和加速度变化图像的变化幅度非常小，说明钢球直径的变化不会使得钢球运动过程中的速度和加速度的变化趋势发生显著的变化。

3 结论

在对“珠子动力学”进行充分分析的基础上，推导了钢球从圆环最高点运动到最低点的过程中，钢球的速度和加速度的变化规律。并利用Python语言编程进行了数值模拟，得到了相关因素对钢球运动过程中速度和加速度变化趋势的影响。

钢球从圆环最高点运动到最低点的过程中，其速度逐渐增加，在最低点处达到速度最大值;其加速度先增加后减小，在1/4圆环处达到加速度最大值;圆环的半径对钢球运动速度的变化有较大的影响，且随着圆环半径的增大，钢球通过圆环同一位置时的速度相应增大，且钢球运动到最低点时的速度与圆环半径的1/2次方成正比;圆环的半径对钢球运动加速度的变化趋势影响较小;钢球的直径对钢球运动速度和加速度的变化趋势影响较小。在后续的研究中，将继续设计实验，利用相关实验数据进一步证明观点的准确性。

参考文献：

〔1〕苏振超，薛艳霞.论理论力学中摩擦力和摩擦角概念的引入[J].力学与实践，2012，34（01）：96-99.

〔2〕沈志斌.动量守恒定律的三个重点[N].中国教育报，2003-02-19（T00）.

〔3〕盖晓丹.例谈动量守恒定律中碰撞问题模型的教学设计[J].读写算，2019，35（13）：181.

〔4〕辛景凡，孙佩箫，熊宇玲，等.表面张力测定实验的改进——冒泡速度对其影响的初探[J].赤峰学院学报（自然科学版），2021，37（04）：21-24.

〔5〕Scholz Veronika， Winkler Peter， Hornig Andreas et al. Structural Damage Identification of Composite Rotors Based on Fully Connected Neural Networks and Convolutional Neural Networks[J]. Sensors， 2021， 21（06）.

〔6〕王晓辉，刘清荣，郭楠.基于逆向工程的三维曲面重构软件的研究[J].赤峰学院学报（自然科学版），2015，31（03）：44-45.

〔7〕姚建盛，李淑梅.Python在科学计算中的应用[J].数字技术与应用，2016，34（11）：76.

〔8〕祁玲敏，韩太坤，贺言，等.Origin软件在PN结伏安特性实验数据处理中的应用[J].物理通报，2019，69（06）：90-93.