基于时间序列分析法对贵州省地区生产总值的预测

◎贺文侣 张会暄

国内生产总值(GDP)是衡量一个国家经济状况的重要指标,对促进经济增长和协助地方经济决策具有重要意义。本文对贵州省2005-2019年的56个季度GDP数据基于SPSS23.0用确定性分析消除季节效应后通过ARIMA模型进行拟合，通过对数据误差分析、模型参数估计、模型检验等综合分析，确立了符合趋势性和周期性特点的ARIMA模型。再用软件预测未来2年贵州省GDP总值，最终得出未来2年贵州省GDP将逐年稳定上升的特点。

一、引言

不论是发达国家还是发展中国家，追求经济增长是世界各国永恒的主题。国内生产总值，简称为GDP，是指一个国家或地区在一定时期内（通常为1年）所有常住单位所生产的全部最终产品和劳务的市场价值，反映了该国或地区经济的实力和发展状况。地区生产总值（地区GDP）是指本地区所有常住单位在一定时期内生产活动的最终成果，地区生产总值等于地区内各产业增加值之和。1993年，中国正式取消国民收入核算，GDP成为国民经济核算的核心指标。2014年国家统计局积极稳妥地推进国家统一核算地区生产总值，制定经济核算图，指定全国统一的核算办法。为反映贵州省的经济发展情况，本文对贵州省2005-2019年的56个季度GDP数据进行分析和检验，并利用时间序列分析的相关理论建立ARIMA模型，最后根据模型结构对未来近2年的贵州省地区GDP进行预测。

二、数据来源

本文所采用的数据为我国2010年至2019年贵州省地区生产总值季度数据，所需数据均来源于中华人民国国家统计局。

三、统计预测与分析

（一）数据处理

时间序列模型是建立在随机序列平稳性假设基础上，因此时间序列的平稳性是建模的重要前提。任何非平稳时间序列只要通过适当阶数的差分运算就可以实现平稳。

1.数据平稳性检验。

本文采用数据图检验法判断序列平稳性。首先对数据进行平稳性检验。利用SPSS23.0软件做出2005年第一季度至2018年第四季度贵州省地区生产总值时序图，由时序图可知，贵州省地区生产总值呈现明显的趋势性和季节性的变化趋势。从时间上看，2005年以来贵州省地区生产总值逐年递增，序列具有长期上升的趋势；在季节上呈现第一季度、第二季度GDP相对较低，而第三季度、第四季度GDP表现明显增长的态势，贵州省地区生产总值序列属于非平稳序列，因此，需要对其进行差分变换等来消除以上趋势。

2.数据平稳化处理。

对非平稳序列，需要进行平稳化处理再利用ARIMA模型建模。为消除上述趋势减小数据波动，首先对贵州省地区生产总值的时间序列进行一阶差分，提取原序列的趋势效应。经过一阶差分提取原序列线性递增的信息，序列趋势性得到很好地消除，但由一阶差分后的自相关图观察，一阶差分后序列仍呈现以年为周期的季节性波动，为此，我们需要进一步做季节差分以消除这种趋势。进行季节差分后的序列仍表现出较大的趋势性，故我们继续对其采取自然对数转换，进行一阶差分、季节差分、对数转换的序列趋势性和季节性得到了较好的消除，序列中虽然存在一些异常值，但是总体波动幅度基本趋于一致，已经达到了消除异方差非平稳性的目的，可以考虑建立时间序列模型。

3.数据纯随机性检验。

由于并不是所有的平稳时间序列都是值得研究建立模型的，只有序列值彼此之间具有密切的相依性，历史数据对未来的发展有一定影响，这样的时间序列才值得研究。因此，利用SPSS对平稳化的一阶季节差分序列进行纯随机性检验。可知显著性均小于置信水平0.05，认为该序列不属于纯随机序列，这些数据间是自相关，还包含着值得提取的信息，可以考虑建立模型。

（二）模型的建立与识别

1.ARIMA模型的理论知识。

在预测中，对于平稳的时间序列，可以使用自回归移动平均（ARMA）模型及特殊情况的自回归（AR）模型、移动平均（MA）模型等来拟合，预测改时间序列的未来值，但在实际的经济预测中，随机数据序列往往都是非平稳的，此时就需要对该随机数据序列进行差分运算，进而得到ARMA模型的推广-ARIMA模型。

ARIMA模型全称综合自回归移动平均模型，简记为ARIMA（p，d，q）模型，其中，AR为自回归，p为自回归阶数；MA为移动平均，q为移动平均阶数；d为时间序列成为平稳时间序列时所做的差分次数。ARIMA（p，d，q）模型的实质就是差分运算与ARMA（p，q）模型的组合，即ARMA（p，q）模型经d次差分后，便为ARIMA（p，d，q）。

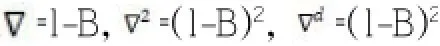
式中，d为差分的阶。

季节差分：季节差分中k一般取一个周期，如对于月度数据k=12，对于季度数据k=4，等等，季节差分的算子为：

设｛Z｝t为非平稳序列，｛X｝t为ARIMA（p，q）序列，存在正整数d，使得｛X｝t=Zt，t＞d，则有：

称此模型为综合自回归移动平均模型，记为ARIMA（p，d，q）。

2.模式识别。

利用SPSS时间序列分析中的专家建模器自动识别模型为ARIMA（0，0，0）（0，1，1）。

从模型拟合度表（表3-1）可以看出，R方为0.998，模型拟合很好，调整后贵州省地区生产总值模型的统计量，见表3-3在95%的显著性水平下，Ljung-BoxQ统计量为20.259，其P值等于0.164，明显大于统计学显著性意义，结论支持了原假设（H0：模型不是自相关序列，H1：模型是自相关序列），得出模型不存在序列自相关的结论。

表3-1模型统计表

（三）模型的检验

对已经建立的模型最重要的是检验整个模型是否充分提取完了序列数据的有效信息，即检验其残差序列是否是白噪声序列。如果拟合的最优模型残差序列是非白噪声序列，就要继续调整模型。如果残差序列是白噪声序列，此时就认为拟合的模型是有效可行的。通过残差序列图进行检验，可知残差序列的自相关和偏自相关函数都是0阶截尾，因而残差是一个不含相关性的白噪声序列。因此，序列的相关性都已经充分拟合了。

（四）模型的预测

为了验证模型的实际预测效果，首先用得到的模型对2019年四个季度的贵州省地区生产总值进行试测验所示，计算的真实值与预测值的误差率绝对值最大的不超过0.1562，最小的为0.0179，说明预测值与真实值较为接近。

根据2019年四个季度观测的实际值进一步修正模型后，得到2020—2021年8个季度GDP预测值见表3-2。从预测结果上看，地区生产总值仍然延续以往的增长规律，每年的第四季度都是一年中的最大值，这和往年的变化规律是一致的。

表3-2 2020-2021每个季度贵州省GDP预测

四、总结

文章根据2005-2019年贵州省地区生产总值季度统计数据，检验数据的平稳性可知该数据为非平稳数据，然后对原始数据通过差分变成平稳序列，利用一阶差分后的平稳数据对贵州省2005-2019年的56个季度时间序列数据建立ARIMA模型，在此基础上对贵州省近2年的GDP进行预测，并对预测结果进行了验证。结果表明，该模型能较好地预测贵州省近2年的地区生产总值，且预测精度较为精确，预测结果可以为政府实施相关宏观、微观经济政策提供参考。