面向多数据中心跨节点环境的公安大数据分析方法

杨 杰,邓旭冉,翟春婕

(1.江苏省公安厅， 江苏南京 210024； 2.新疆生产建设兵团公安局， 新疆乌鲁木齐 830002；3.南京森林警察学院信息技术学院， 江苏南京 210023)

0 引言

近年来，随着公安大数据战略的全面实施，公安大数据分析应用进入高速发展期，迅速成为学术界、产业界研究的新热点，提出了一系列技术实现方法，在服务公安工作中发挥了重要作用[1-3]。但随着公安实战应用的不断深入和数据增长的不断提速，现有分析方法的瓶颈越来越为明显：①现有方法大多基于存储在同一数据中心甚至是单一Hadoop集群的数据开展分析[4-5]，但当前公安数据资源大多按属地或业务归属分散存储在市、县级公安机关或职能警种的数据中心，若将数据向统一的公安大数据中心物理集中后再开展分析，抽取传输时间、云平台资源消耗等都存在极大成本，且部分警种的数据资源因政策限制只能存储在本警种数据中心，不能向统一的公安大数据中心开放汇聚。②现有方法大多基于全量数据开展分析[6-7]，但当前的公安数据资源不仅总量是大数据，周期内的增量也具有一定规模的数据量，若每个更新周期后总是基于新的全量数据开展分析，其运算时间会随着更新周期的增加而急速增长，很容易导致分析结果因不符合时效要求而失去实战价值。上述两个问题，使得现有分析方法要么在多数据中心分布式数据存储环境下无法有效执行，要么运算时间过长无法满足实战应用的高时效要求。李伟等人[8]的研究也表明，将12亿条“电子警察”抓拍车牌数据从不同的Oracle数据库抽取集中到统一的HDFS存储环境，耗时长达3小时10分钟；在10台PC服务器组成的Hadoop集群中以40个初始Map执行套牌车分析模型，完成上述12亿条数据的计算耗时长达50分钟。

图1 公安大数据多数据中心跨节点分布式分析技术框架

1 多数据中心跨节点分布式分析技术框架

上述典型问题，国内各大运营商和互联网企业在其技术发展过程中也都先后经历过，到现阶段都走向了以云计算为基础的多数据中心分布式协同的技术路线[9-10]。本文针对公安大数据应用需要，研究提出一种多数据中心跨节点协同的分布式分析技术框架，支持公安大数据在不需要物理集中、多节点分区分域存储条件下，实现跨多个数据中心的分布式协同分析、多节点并行分析和可持续增量分析。其主要思想是：借鉴边缘计算模式，将下级公安数据中心或横向警种数据中心作为边缘节点，并指定一个汇聚节点。实现过程中，将公安大数据分析的具体算法拆解为按序先后执行的若干步骤：首先，在各边缘节点完成节点本地计算步骤，得到局部结果集，不同边缘节点之间执行相同的算法步骤，形成并行计算；然后，将各边缘节点局部结果集传送到指定的汇聚节点，并在汇聚节点完成全局计算步骤，得到全局结果集。更进一步，在每个增量周期末，对新增的数据按上述策略在各边缘节点并行完成局部计算，计算结果在与本节点已有局部结果集合并的同时传送到汇聚节点，然后在汇聚节点完成已有全局结果集与各边缘节点增量计算结果集的全局合并，从而同步实现局部结果集和全局结果集的可持续增量更新。上述过程重复迭代，就实现了公安大数据分析的多数据中心跨节点分布、并行、增量计算，既破解了现有分析方法在公安数据资源多数据中心跨节点分布式存储条件下无法执行的问题，又破解了每次分析运算只能基于全量数据开展的困局，极大提高了计算效率和结果准确性，其基本流程如图1所示。

2 公安大数据分布式分析的应用实现

基于上述多数据中心跨节点分布式分析技术框架，本文进一步研究提出了公安大数据分析方法的分布式并行增量计算实现方法，主要采用较为常见的规则统计类分析和算法建模类分析。

2.1 规则统计类分析应用的分布式并行增量计算

规则统计类分析应用，主要是以各类业务规则为判断条件，进行条件比较、算术计算和计数统计等运算，以应用极为广泛的轨迹伴随分析为例，其实现过程如下：

(1)将确定的伴随分析运算规则(时间距离、空间距离、伴随次数等约束条件)分发到每个边缘节点；

(2)在所有边缘节点并行完成本地数据的伴随分析，对符合约束条件的计算结果输出为本节点局部结果集；

(3)将各个边缘节点的局部结果集传送到指定的汇聚节点，进行局部结果集的全局合并计算，得到全局结果集；

(4)当有周期增量数据进入时，就对增量数据重复执行上述过程，并在边缘节点和汇聚节点分别完成增量计算结果与已有存量结果集的合并运算，从而得到新的边缘节点局部结果集和汇聚节点全局结果集。

上述过程整体实现步骤如下：

Step1 分发伴随分析运算规则，给定时间距离、空间距离、伴随次数的阈值组合(t0,d0,c0);

Step2 各边缘节点并行完成本地数据伴随分析：

①根据给定距离公式计算(tnij,dnij)，n∈(1,…,N)为边缘节点序号；

②判断是否满足距离约束条件，若tnij≤t0,dnij≤d0，输出局部结果集(〈IDni，IDnj〉，countnij,stdatenij,ltdatenij)；

③判断是否满足伴随次数约束条件，若countnij≥c0，对象IDni、IDnj确认建立伴随关系；

IDni为节点n中对象i的唯一标识，countnij为截至ltdatenij对象IDni、IDnj在节点n的局部伴随次数，stdatenij、ltdatenij分别为对象IDni、IDnj形成轨迹伴随的起始时间、最后时间，当countkij=1时，stdatekij，ltdatekij分别为两条轨迹中的较小时间、较大时间。

Step3 汇聚节点完成局部结果集的合并运算：

①各边缘节点局部结果集(〈IDni，IDnj〉，countnij，stdatenij，ltdatenij)传送到汇聚节点；

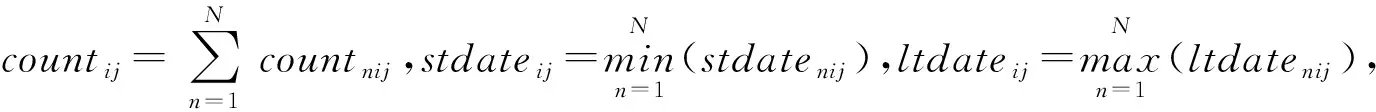
③判断是否满足伴随次数约束条件，若countij≥c0，对象IDi、IDj确认建立伴随关系；

Step4 各边缘节点并行完成增量数据伴随分析：

①合并节点本周期增量数据tni≥min(Δstdaten)-t0的存量数据；

②执行步骤Step2，输出局部增量结果集为(〈IDni，IDnj〉，Δcountnij,stdatenij,Δltdatenij)；

③更新countnij=countnij+Δcountnij，ltdatenij=Δltdatenij，输出新的局部结果集。

stdatenij为Step2的首次计算结果，一旦得出即保持不变，tni为对象IDni的轨迹发生时间，min(Δstdaten)为本增量周期的轨迹发生最小时间，这样，就可以避免因为轨迹数据跨增量周期而有可能导致的伴随关系遗漏。

Step5 汇聚节点完成局部增量结果集的合并运算：

①各边缘节点局部增量结果集(〈IDni，IDnj〉，Δcountnij，stdatenij，Δltdatenij)传送到汇聚节点；

③对未建立随便关系的对象IDi、IDj，判断是否满足伴随次数约束条件，若countij≥c0，则确认建立伴随关系。

2.2 算法建模类分析应用的分布式并行增量计算

算法建模类分析应用，主要是基于各类机器学习算法，针对潜在风险群体监测、案事件预测等新型应用需求进行建模分析，以挖掘民警常规工作经验无法发现的高价值情报线索。以基于Kmeans算法的潜在风险群体挖掘应用为例，其实现过程如下：

(1) 将每个边缘节点的人员相关数据按标准数据结构完成初始化，并任意选择K条轨迹X1,X2,…,XK作为初始全局聚类中心(即共有K个类)分发到参与运算的N个边缘节点；

(2)在边缘节点n(n∈N)，按照给定的距离计算公式完成本节点待聚类数据Xnl与K个初始全局聚类中心的距离运算，并根据计算结果将所有待聚类数据分配到与其最近的类k输出为 (k,Xnl)，具体距离计算公式可根据具体应用需要作针对性选择；

(3)在边缘节点n，对距离计算输出的(k,Xnl)按照给定的求和计算公式进行合并并输出为本节点的局部结果集(k,〈Nnk,Cnk〉)，Nnk为本节点划入局部类k的数据数量，Cnk为局部类k中Xnl的计算维度值和；

(4)局部结果集(k,〈Nnk,Cnk〉)传送到汇聚节点并完成全局合并，输出结果为(k〈Nk,Ck〉)；

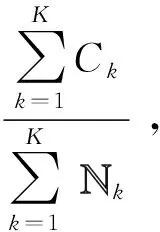
(6)当有新的周期增量数据进入时，就以上一周期所得聚类中心为初始聚类中心，对每个边缘节点的本周期增量数据执行步骤(2)～(4)，所得结果与已有存量(k〈Nk,Ck〉)合并后再执行步骤(5)，从而得到新的聚类；

(7)每一周期所得类确定后，根据类中数据所属人员对象，生成潜在风险人员群体。上述过程整体算法步骤如下：

Step2 计算空间距离，确定本轮迭代节点内局部类划分：

①根据选定的距离公式分别计算Xnl与K个聚类中心X1,X2,…,XK的距离dl1,dl2,…,dlK；

②根据dl1,dl2,…,dlK的最小值确定Xnl所属的类k；

③随机选择另一待聚类数据X′nl，转step2 ①；

④输出边缘节点n的聚类结果(k,Xl)；

Step3 边缘节点n聚类结果合并：

①统计类k的数据数量Nnk；

②根据

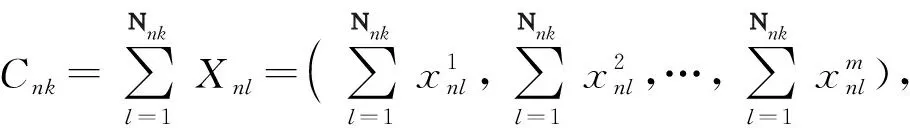
③输出边缘节点n的局部结果(k,〈Nnk,Cnk〉)，并传送到汇聚中心；

Step4 各边缘节点局部结果合并：

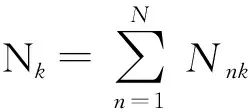
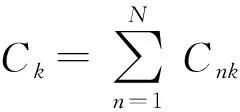
③输出全局结果(k,〈Nk,Ck〉)；

Step5 全局结果收敛性判断：

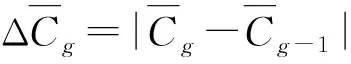
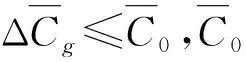
Step6 增量数据聚类运算：

②合并增量聚类结果与已有存量聚类结果Nk=Nk+N′k，Ck=Ck+C′k；

③输出边缘节点n的局部增量聚类结果(k,〈Nnk,Cnk〉)，并传送到汇聚中心；

④执行Step5，输出本周期增量聚类全局结果。

Step7根据所得类中数据所属人员对象，生成潜在风险人员群体。

3 实例验证及性能测试

实验选取了5个广域分布的公安数据中心，每个数据中心按标准数据结构提供20 GB轨迹数据，依次指定中间某一数据中心为汇聚节点，基于伴随分析模型开展实验测试。测试结果表明，基于本文所提出的多数据中心跨节点分布式分析技术框架，很好地实现了伴随分析计算步骤的跨数据中心节点分布式并行执行，在极大提高分析计算效率的同时，有效解决了传统方法只能基于本地数据开展分析的技术瓶颈，突破了层级之间、警种之间数据必须向某一数据中心物理集中的技术限制。同时，通过建立增量分析机制，实现了可持续增量迭代的伴随关系分析，进一步提高了计算效率。经专业性能测试，较以往基于单一节点物理集中数据资源开展分析的方法，跨节点分布式并行分析的时间消耗平均缩减3/4以上，进一步建立增量分析机制后，在单考虑每个周期增量数据计算时长的情况下，时间消耗平均缩减超过8成。测试整体分两步：

首先，对比测试跨节点分布式并行分析与单节点集中式分析两种轨迹伴随分析方法的时间消耗，待分析的轨迹数据总量为100 GB，计算过程中5个数据中心各承担一次汇聚节点角色。其中，跨节点分布式并行分析是由5个节点并行完成20 GB轨迹数据的伴随分析，其中4个节点的分析结果汇总到指定的汇聚节点后与汇聚节点的计算结果一起完成全局合并。测试过程中发现，较每个节点完成20 GB轨迹数据伴随分析的时间，分析结果的传输汇总时间和在汇聚节点的合并时间均可忽略；单节点集中式分析是从每个节点将20 GB轨迹数据抽取到指定的汇聚节点后开展伴随分析，抽取汇聚的平均时长为0.86小时。具体执行时间如表1所示。

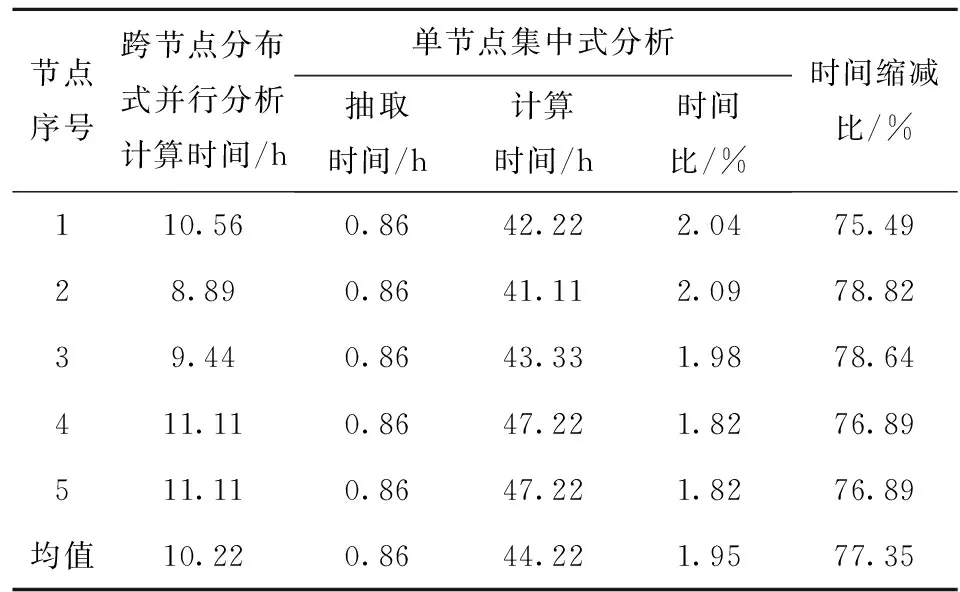
表1 跨节点分布式并行分析与单节点集中式

从表1可以看出，在单节点集中式分析方法中，尽管抽取时间较计算时间整体占比较小仅有1.95%，但绝对时间仍然长达0.86小时，在人、财、物高速流动的现代社会，将近1个小时的时间延迟足以给实战应用带来不可估量的影响甚至是颠覆性的影响。进一步对比跨节点分布式并行分析与单节点集中式分析的时间消耗，在避免网络传输时间消耗的同时，由于5个节点可同时以并行化的方式进行分析计算，极大提高了计算效率，时间消耗压降均超过75%。

更进一步，对比测试单节点集中式分析、跨节点分布式并行分析、跨节点分布式增量分析，其中，跨节点分布式增量分析是按照均分的原则，以10 GB为一个节点一个周期的数据增量，由5个节点各完成两个增量周期共计100 GB轨迹数据的伴随分析计算任务，具体结果如表2所示。

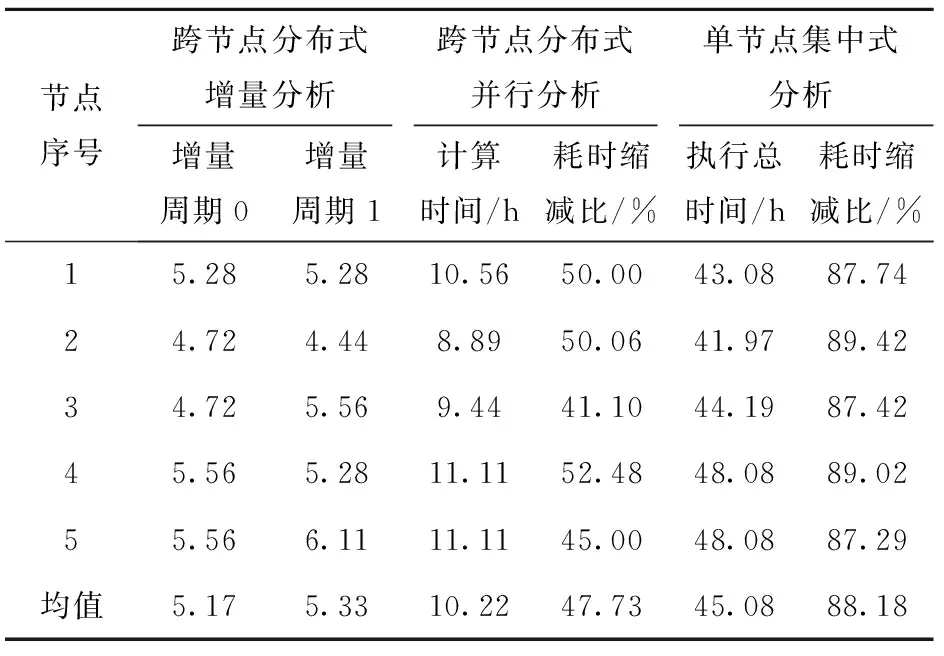
表2 跨节点分布式增量分析、跨节点分布式并行分析、单节点集中式分析时间消耗对比

从表2可以看出，在考虑两个增量周期的分析计算时间总消耗时，跨节点分布式增量分析方法与跨节点分布式并行分析方法每个节点分析的数据总量相同均为20 GB，同一节点两种方法所需的总时间也大致相同，平均偏差仅有2.9%。但跨节点分布式增量分析方法由于设计了增量机制，在完成增量周期1的分析任务时，仅需对本周期的增量数据进行计算，而无需考虑增量周期0的已消耗时间；若采用跨节点分布式并行分析方法，则每个增量周期各节点都需对本节点的全量数据进行计算。从表2可以看出，仅完成一个增量周期的分析任务，时间消耗平均就缩减了47.73%，随着增量周期的增加，两种方法的时间消耗差值必将进一步扩大，在当前公安大数据多以时间戳为增量标志位的现实情况下，建立基于时间戳的增量分析机制，如以24小时为一个增量周期，以定制计划任务的方式每日固定时间执行前24小时增量数据的分析计算，在实战中能够极大缩短分析任务的运算时间，具有很强的实用意义。在具体工作实践中，所有类似分析任务笔者均采用依数据更新时间设定增量周期的方式，如某类数据业务更新时间为每日0时、12时、18时，且分析历次更新任务后发现执行时间均不超过20分钟，则设定增量分析任务启动时间为0时30分、12时30分、18时30分，这样就很好地实现了数据采集更新与分析应用的衔接，进一步缩短了服务实战的响应时间。再比较跨节点分布式增量分析方法与单节点集中式分析方法，时间消耗缩减更为明显，在仅完成第一个增量周期分析任务时，平均缩减比就达88.18%。

4 结语

随着5G网络和物联网技术的全面普及应用，公安大数据必将进入新的历史时期，其体量规模和增长速度较当前都将以数量级甚至指数级持续提升，摒弃建立单一超大规模数据中心物理汇聚全量数据开展大数据应用的传统理念方法，构建不同警种、不同层级公安机关多数据中心分布式协同的公安大数据技术体系、应用方法和增量机制，也是破解公安大数据技术瓶颈、政策制约的有效方法，是支撑公安大数据应用开展的必然选择，更是保障公安大数据智能化建设的科学路径。