借助画图之力 开启思维之门
杨 强
画图是数学教学中最基本、最常用的方法之一。通过画图,能够帮助学生把抽象的数学问题具体化、形象化、直观化,从而使他们能从图中理解题意、理解概念,分析数量关系,寻找解题思路,既能培养学生思维能力,又能发展数形结合能力。画图是小学生解数学题时必不可少的能力,能够借助图形表征和分析问题,使复杂的数学问题变得简明、形象,更有利于启发学生寻找解决问题的思路。画直观形象的图,可以让学生从触觉、视觉等多方面进行体验,进而有效地促进数学思维的发展。为此,教学时教师应循序渐进地培养学生读图、画图、析图的能力,激发学生画图的意识。
一、以“图”建“数”,凸显简洁数学
数学教学中有许多种解决问题的策略,而画图是一种最基本的策略。通过画图,能够把一些抽象、复杂的数学问题形象化、简单化。
例如,著名特级教师徐斌在执教“画线段图解决问题”(倍数关系的线段图)时,在“形”的简洁价值体验中就做了很好的示范。徐老师的课件中先出示了2 朵红花和8 朵蓝花,然后用动态图将花变成大小相同的正方形,正方形又变成长方形……直至拼成的长方形上面的长消失。至此,线段图就形成了。从研究实物入手,到半抽象的图形及最后用抽象的线段图表示倍数关系,整个教学过程中都在引导学生思考“什么变了、什么没变”这一关键问题,让学生经历了倍数线段图的产生、发展、形成的全过程。为了充分体验线段图的简洁性,徐老师还设置了这样的环节:把同一个问题分别用情境图呈现和用线段图表示,让学生选择喜欢哪种表示,并说明理由。学生异口同声地指向线段图,理由为线段图简洁,从图上能看到几个几。由此可见,徐老师的“无痕教育”,让二年级的学生体验到了“形”的简洁作用,体现了简洁数学。
二、以“图”解“数”,寻找解题思路
小学生的思维主要停留在形象直观层面,抽象思维发展尚不完整。复杂的信息和抽象的数量关系常常成为低年级学生的绊脚石。借助图形的帮助,能够使学生在形象思维与抽象思维之间搭建起一座桥梁,从而帮助其寻找解决问题的思路。
例如,在教学人教版一年级下册“求一个数比另一个数多几(或少几)”这一知识点时,可以从画图入手,找出解题方法。
教师出示:

提出要求:请你画△,让别人一眼看出比○多3 个。
学生尝试:
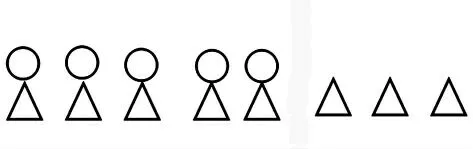
教师请学生评价他的做法。
生:他用“一一对应”的方法比较,用虚线把△隔成两部分,虚线左边△表示和○同样多,虚线右边有3 个,这样一眼看出△比○多3 个。
教师再出示例题:小雪说:“我套中了7 个。”小华说:“我套中了12 个。”小华比小雪多套中几个?你知道了什么?
生:小雪套中7 个圈,小华套中12 个圈这两个信息,问题是小华比小雪多套中几个?
师:你想怎样解答?
生:我想把他们两个套中的圈画出来比较。
师:画图可以让题目的意思更简单明了,方便找寻解题方法。大家试着画一画,并列式计算。
指名汇报:用○表示小雪套中的圈,用△表示小华套中的圈。

生:用“一一对应”的方法分别表示出两个信息,再请虚线帮忙,把小华套中的12 个分成两个部分,左边部分表示和小雪同样多的7 个,那么右边的剩余部分就是“小华比小雪多套中的个数”,并把它圈出来。所以12-7=5(个)。
教学中,有了前面导入的铺垫,解决例题时学生能够较快地得到启发:通过画图与运用“一一对应”的比较方法,可以很快在图中找到问题所在。既理清了信息中的数量关系,降低了解决问题的难度,又丰富了减法算式的含义。这样,学生不仅能把已知信息完整准确地画出来,找出问题,而且还能学会有条理地表达自己的想法。此外,学生手、口、脑并用,既活跃了数学思维,又培养了动手操作能力与口头表达能力。
三、以“图”想“数”,厘清解题思路
通过画图,把题目的意思表达出来,帮助学生化抽象为直观,化复杂为简单,化隐性为显性,化无序为有序,从图中找到解题的突破口,从而厘清解题的思路。
例如,明明、红红、芳芳、强强和敏敏5 个人进行羽毛球比赛,规定每两人都要打一场,明明现在已经打了4 场,红红打了3 场,芳芳打了2 场,强强打了1 场,请问敏敏一共打了几场? 分别是和谁打的?
只看题目,学生往往无从下手,这时我们可以简单地画图:
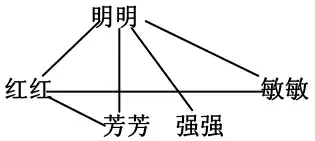
通过画图可以知道,明明打了4 场,那么他与其余四人都要打一场;强强打了1 场,这一场是和明明打的;红红打了3 场,除明明外,她还要和芳芳和敏敏各打一场;此时,芳芳就已经打两场了,分别是和明明、红红。从图中一眼就能看出敏敏共打了2 场,分别是和明明和红红打的。到此,问题顺利得以解决。
借助画图,能让解题的思路更清晰,根据题目所给的条件,把图不断完整,最后根据所画的图就能很快地找到结果。
四、以“图”究“数”,体现直观作用
小学数学教学中有很多关于“数”的问题可以借助于“形”来帮助解决。因此,在教学中通过“以形助数”“以形解数”,既能够体现图形直观的作用,又能提高学生的解题能力。
在解决分数问题时,可以出示这样的经典题目:这座石碑里安葬着古希腊数学家丢番图。他生命的是幸福的童年,再活了寿命的,脸颊上长出了细细的胡须,又过了生命的他才结婚,婚后五年有了一个孩子,孩子活到他生命的便死去了。孩子死后,丢番图在深深的悲哀中又活了四年后也去世了。
教师引导学生和之前简单地求“1”的题进行对比,丢番图碑文中的单位“1”是一样的,他年龄的各个阶段都是他寿命的一部分,这道题有很多个部分,学生会惊奇地发现这道题就是他们最近学的《分数混合运算(三)》。
五、以“图”析“数”,分析数量关系
随着学生知识的不断丰富,单单凭借抽象思维已经不足以应付一些难题。特别是求倍数、分数(百分数)等问题时,这些难题对学生来说十分抽象,如果分析不清楚单位“1”和数量关系,就很容易出错。
例如,“比一个数的几倍多几或少几,求这个数”的题目:红花有60 朵,比黄花的3 倍少9 朵,黄花有多少朵?
学生的错误解法有:60×3-9;60÷3-9;60÷3+9。
而为什么用(60+9)÷3 列式,很多学生很难理解。这时,可以借助线段图进行分析,弄清数量关系。
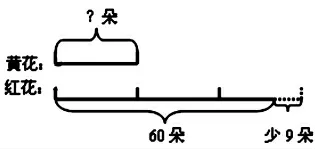
从图上可以清楚地看出,黄花是一倍数,60 朵红花还不到黄花的3 倍,比黄花的3 倍少9 朵。60 朵加上9 朵正好是黄花的3倍,则列算式为(60+9)÷3。这样,借助线段图,能化抽象为直观,进而帮助学生分析数量关系。
总之,在小学数学教学中,教师应具有“一图抵百语”的意识,借助画图,丰富学生的表象认识,启迪学生的思维。充分利用学生形象思维的特点,以“形”助“数”,展现知识的建构过程,从而培养学生的思维能力。

