天然气水合物钻采船隔水管力学特性分析

高 杭 李小易 刘 放 马海峰 陈 勇

（1.四川宏华石油设备有限公司，四川 成都 610036；2.西南石油大学机电工程学院，四川 成都 610500）

0 引言

中国的天然气水合物分布广泛，其中南海海域是资源最丰富的地区之一，但在天然气水合物开发的过程中，出现了一系列的新问题。海洋钻井中，隔水管系统作为连接海洋钻井平台与海底井口之间的重要部件，是非常薄弱的环节，也是海洋钻井开发的瓶颈［1-3］。当隔水管的固有频率与海流产生的涡激频率接近时，将产生涡激振动，导致隔水管产生横向位移，显著降低隔水管的疲劳寿命。钻井隔水管除了承受自身重量以外，还承受了严重的机械载荷，如海流及恶劣的海况等［4］。因此对于隔水管的固有频率以及动力响应分析是非常有必要的。

1 研究现状分析

国内外学者进行了大量理论和实验研究，畅元江［5］等基于能量守恒定律提出了隔水管固有频率的简化计算公式，其计算结果与相关文献计算结果比较吻合；Guo Haiyan［6］等利用有限元方法研究了内部流体流速和顶张力对隔水管固有频率的影响，结果表明内部流体流速越大，固有频率越小；邵卫东［7］等考虑浮体升沉及张紧环运动，提出了一种计算深水中顶张力立管固有频率的方法。Montoya-Hernandez，D.J［8］等提出了一种计算多相流状态下刚性生产立管振动的数值方法，计算了垂直立管模型与水动力数值模型的固有频率。石晓兵［9］等考虑三维载荷对隔水管的作用采用有限元法分析计算了深水钻井隔水管的动力特性。Wang Yanbin［10］等使用变分法推导出隔水管的微分方程，得到了横向振动的表达式，并讨论了最大横向振动位移随隔水管尺寸、防喷器重量、波高和波浪周期的变化。S. Lei，X.Y.Zheng，D.Kennedy［11］建立了立管动态运动的非线性耦合方程，并用中心差分法在时域进行求解，得到隔水管系统平面振动、横向振动和轴向振动之间的耦合效应，进行了隔水管系统的动力响应分析。林海花，王言英［12］利用Hermite 插值函数对隔水管的运动方程进行有限元离散，采用New mark 方法求解，得出波浪海流共同作用下的隔水管涡激动力响应分析。

通过分析和计算南海某油井的隔水管的固有频率、力学特性，进而分析隔水管的动力响应，研究隔水管钻井液密度、顶张力、截面尺寸、水深、波高以及波浪周期等因素对于隔水管固有频率和动力响应的影响，以期给深水钻井工况下隔水管系统的设计提供参考作用。

2 隔水管固有频率研究与计算

隔水管在深水钻井作业中，通过竖直状态来连接钻井平台和海下，会受到顶张力和分布载荷的作用影响［13］，力学模型如图1所示。

图1 隔水管力学模型图

在顶张力T的作用下，隔水管是小变形状态，隔水管的动力响应就理解成无数个不同振幅和频率的正弦波的叠加。隔水管固有频率的简化公式为：

式中， ω 是隔水管的n 阶固有频率，Hz；EI 为隔水管的弯曲刚度，N·m2；T 是近似隔水管中部的平均张力，T＝（Ttop＋Tbot）／2，N。Ttop和Tbot分别为隔水管顶部和底部的张力，N；M是隔水管产生振动时的单位尺寸质量［14］，包含隔水管自身单位长度质量m1、节流和压井管线单位长度质量m2、隔水管内部液体单位质量m3、隔水管外部附加水的单位质量m4以及钻柱的单位长度质量m5，kg。

选取南海某油井的数据，海域水深为1 500 m，海水密度为1 037 kg／m3，隔水管的总长度为1 500 m，隔水管外径为0.609 6 m，壁厚为0.012 7 m，节流和压井管线外径为0.101 6 m，壁厚为0.0119m；隔水管底部有40%超张力，隔水管的弹性模量为2.06×1011Pa，隔水管密度以及节流和压井管线密度均为7 850 kg／m3，隔水管内部液体密度为1 300 kg／m3，钻柱外径为0.127 m，钻柱壁厚为0.01 m，密度为7 800 kg／m3。通过计算可以得出隔水管固有频率的计算结果（表1）。

表1 基本固有频率计算数值表 单位：Hz

3 隔水管固有频率影响因素分析

影响隔水管固有频率的因素有外在和内在因素，外在因素主要包括内部液体密度、张力比和水深，内在因素主要是隔水管的壁厚，在进行影响因素分析时主要需要从以下4个方面进行考虑和研究［15］。

3.1 隔水管内部液体密度对固有频率的影响

隔水管其他参数保持不变时，分别取隔水管内部液体密度为1 200 kg／m3、1 300 kg／m3、1 400 kg／m3以及1 500 kg／m3进行测试发现：隔水管内部液体密度改变时隔水管固有频率的变化情况（图2）。可以看出，在其他参数都保持不变的情况下，隔水管的固有频率随着隔水管内部液体的密度的变大而稍有减小，但减小幅度不大。因此隔水管内部液体的密度对于固有频率的影响不大。

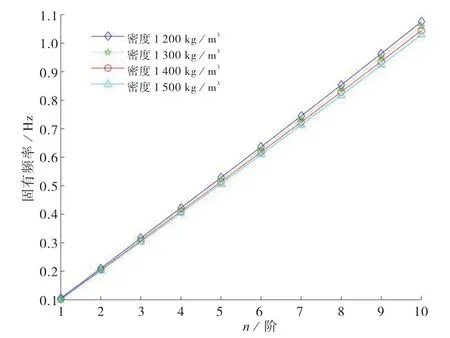
图2 不同内部液体密度下的n阶固有频率图

3.2 隔水管张力对于固有频率的影响

张力比（TTR）是隔水管顶张力Ttop与隔水管浮重G的比值，用R表示。张力比对于深水隔水管是非常重要的性能指标［16］。改变张力比可以改变隔水管的固有频率，令张力比R分别取1.2、1.4、1.6、1.8 时，计算隔水管n阶固有频率的变化（图3）。可以看出，隔水管固有频率随着隔水管张力比的增加而降低，而且降低幅度比较明显，说明控制隔水管的张力载荷是改变隔水管固有频率比较有效的办法。

图3 不同隔水管张力下的n阶固有频率图

3.3 水深对钻井隔水管固有频率的影响

随着世界各地海洋深水钻井勘探作业范围的不断扩大，作业水深也不断增加［17］。由于隔水管张力T随着水深的改变而发生变化，所以隔水管固有频率也会随着水深的改变而改变，任意水深x处的张力为［18］：

式中，l为海域深度，m；G为隔水管的浮重，N。

计算不同水深下的隔水管固有频率，得出水深对隔水管n阶固有频率的影响（图4）。可以看出，水深对于隔水管的固有频率影响较大，所以需要针对水深来进行隔水管的设计以及配置的优化。

图4 水深不同的隔水管n阶固有频率图

3.4 隔水管截面尺寸对于固有频率的影响

隔水管外径为0.609 6 m 保持不变，规定隔水管壁厚分别为0.012 7 m、0.015 9 m、0.019 1 m、0.025 4 m，隔水管的浮重和张力T 也随着隔水管壁厚的变化而发生改变，则可考察隔水管的固有频率随壁厚的变化情况（图5）。可以看出，隔水管外径不变时，隔水管的固有频率随隔水管壁厚增加而增加，而且变化幅度相对明显。因此在进行隔水管的设计时也需要根据实际工况考虑到隔水管的壁厚。

图5 不同隔水管截面尺寸的n阶固有频率图

4 隔水管系统动力响应分析

隔水管系统在海水中常受到的是波浪力和海流力所产生的横向负载，以及由于自重与浮力引起的纵向负载。钻井隔水管的受力可以简化为发生大应变，但对于产生小变形的纵横弯曲梁，横向载荷为动载荷，就会导致隔水管发生振动。隔水管的力学模型如图6所示。

将隔水管系统看成是上、下边界约束的简支梁，其运动微分控制方程为：

式中，EI 为隔水管的弯曲刚度，N·m2；T 为隔水管的平均张力，N；m 为隔水管的单位长度质量，Kg；F（x，t）为隔水管所受的波浪力，N。

波浪力fH由水平拖曳力fD和水平惯性力fl组成的，是由波浪水质点的水平速度u 以及水平加速度引起的作用于隔水管的力。

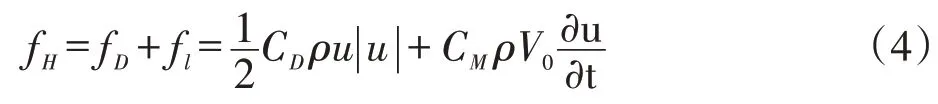
图6 隔水管力学模型图

式中，CD为拖曳力系数，无因次；V0为单位柱体高度的排水体积，m3；CM为惯性力系数，无因次。

隔水管系统有四个边界条件，上下两端分别两个，由于隔水管下端是球形铰支座铰，并且可以转动，假定旋转刚度为K；大多数情况下使用的隔水管上端横向运动都是根据上端连接的浮式钻井平台和钻井船的横向移动来确定的，通常用浮式钻井平台和钻井船的横向移动S（t）来描述，同时隔水管上端与浮式钻井平台和钻井船连接处也存在着旋转刚度Ku［19］，则边界条件为：

4.1 隔水管动力响应

某海域水深为200 m，海浪的最大波高为15 m，振动周期为13 s，海水密度为1 037 kg／m3，隔水管总长度为200 m，隔水管外径为0.609 6 m，壁厚为0.012 7 m，节流和压井管线外径为0.101 6 m，壁厚为0.011 9 m；同时隔水管底部有40%超张力，隔水管的弹性模量为2.06×1011Pa，隔水管密度为7 850 kg／m3，节流和压井管线密度与隔水管密度相同，隔水管内部液体密度为1 300 kg／m3，钻柱外径为0.127 m，钻柱壁厚为0.010 m，密度为7 800 kg／m3。通过计算得出隔水管的动力响应以及最大位移处的振动变化（图7）。

图7 隔水管的动力响应图

从图7中可以看出隔水管最大横向位移出现在隔水管的中部以下，隔水管的最大横向位移发生在水深为132 m 处，该处的最大横向位移为2.941 m，而132 m处的最大振动位移发生在3.21秒，最小振动位移发生在10.1秒，两者相差大约为6 m，这对于隔水管的耐弯曲能力是极大的考验。

4.2 隔水管动力响应影响因素分析

4.2.1 张力对隔水管动力响应的影响

在研究分析中发现张力T对于隔水管的影响是非常大的。在其他条件保持一致的情况下，分别设定隔水管张力比为1.1、1.2、1.3 和1.4，可以得到隔水管位移变化以及隔水管同一位置处随着时间的振动变化（图8）。

图8中可以看出隔水管张力对于隔水管横向振动位移的影响较大，随着张力比的增加，隔水管的橫向振动位移快速减小。当隔水管张力比为1.1时，隔水管的横向振动位移最大，大约为3.962 m，而隔水管张力比为1.4 时，隔水管的最大横向振动位移为2.941 m。132 m 处隔水管最大振动位移都发生在3 s左右，最小振动位移发生在10 s左右。所以在实际工作中，为了保证隔水管以及钻井人员的安全，应尽量保障隔水管有较大的张力比。

4.2.2 隔水管壁厚对隔水管动力响应的影响

从图9可以看出隔水管的壁厚对于隔水管横向振动位移同样有着很大的影响，隔水管橫向振动位移随壁厚的增加而快速减小。隔水管壁厚为0.0127m时，隔水管的横向振动位移最大，大约是2.941m，壁厚为0.0254mm 时，隔水管的最大横向振动位移为1.622m。所以在实际工作中，设计隔水管时要慎重考虑壁厚。

图8 隔水管的动力响应图

图9 隔水管的动力响应图

4.2.3 波浪周期对隔水管动力响应的影响

波浪是作用在隔水管上的一个重要环境载荷，为了研究波浪周期对于钻井隔水管横向位移的影响［20］，取波浪周期分别为13 s、15 s、18 s 和20 s 来研究波浪周期对于隔水管动力响应的影响，得到隔水管的动力响应变化，波长也会随着波浪周期的变化而变化（图10）。

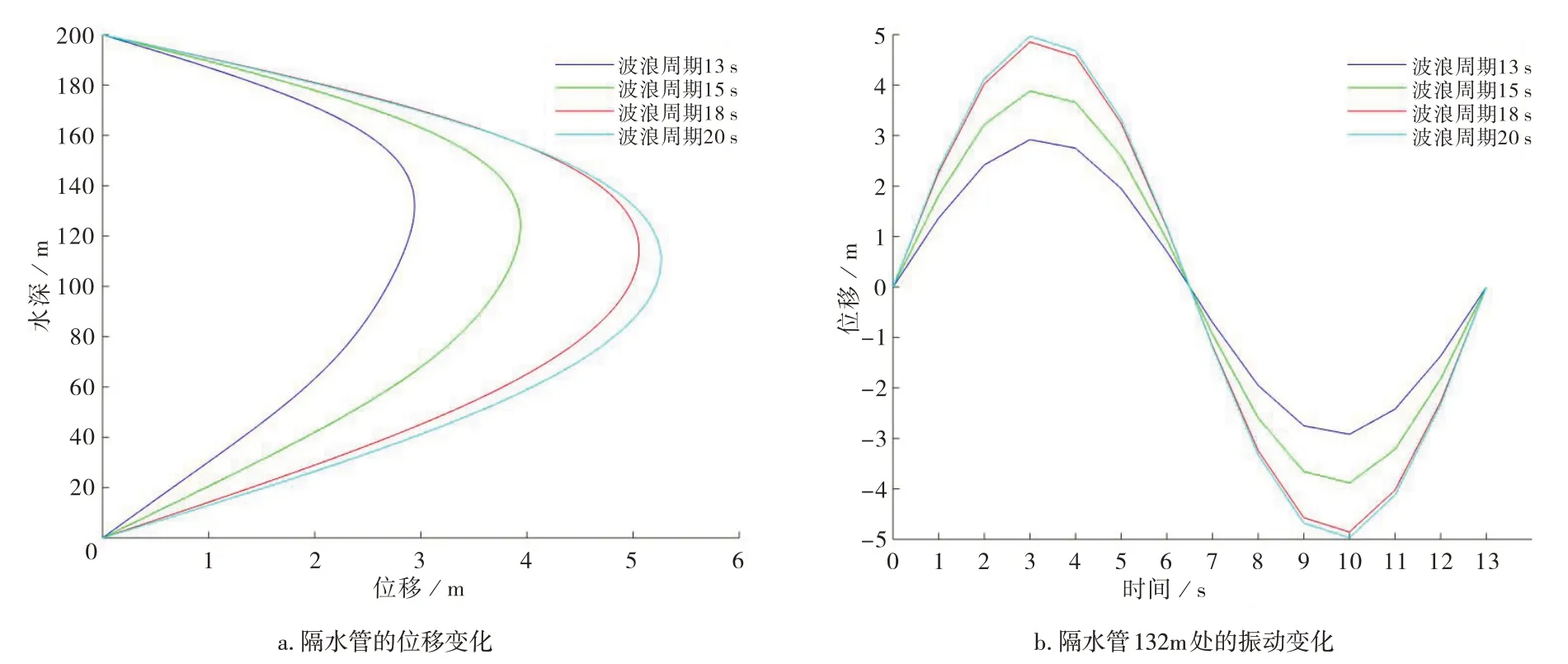
图10 隔水管的动力响应图

波浪的周期会影响波长和波速，从而就会对隔水管的动力响应造成影响，可以看出隔水管最大振动位移会随着波浪周期的增加而增加，在周期为20 s的时候隔水管最大振动位移最大为5.265 m，并且发生最大横向振动位移的水深会随着周期的增加而减小。

4.2.4 波高对隔水管动力响应的影响

在其他条件参数都不改变的情况下，改变波浪的高度，波速以及波浪力就会随之发生变化，从而影响到隔水管的动力响应。因此应研究波高对于隔水管动力响应的影响，取波高分别为10 m、12 m、15 m和17 m，得到的动力响应结果（图11）。

从图11 可以看出，在其它条件不变的前提下，隔水管横向位移随着波高的增加而变大，并且幅度很大。当波高为17 m 时，最大的隔水管横向振动位移约为3.7 m；当波浪高度为10 m时，最大的隔水管横向振动位移只有1.307 m。隔水管最大振动位移会随着波高的增加而增加。

图11 隔水管的动力响应图

5 结论

1）通过对隔水管固有频率的各种影响因素进行计算和分析，确定了钻柱截面尺寸、隔水管截面尺寸、顶部张力比、隔水管内部液体密度和水深等因素均对隔水管n阶固有频率有相应的影响。其中隔水管截面尺寸和顶张力对于隔水管的固有频率影响最大，因此在进行隔水管设计时应根据实际工况考虑两者的影响。

2）通过对隔水管的动力响应进行分析和计算，得到200 m 长的隔水管最大横向位移发生在水下132 m处，位移为2.941 m。

3）随着张力比的增加，隔水管的橫向振动位移快速减小；隔水管的壁厚对于隔水管横向振动位移同样有着很大的影响，隔水管橫向振动位移随壁厚的增加而快速减小；隔水管最大振动位移会随着波浪周期的增加而增加，在周期为20 s的时候隔水管最大振动位移最大为5.265 m，并且发生最大横向振动位移的水深会随着周期的增加而减小；隔水管最大振动位移会随着波高的增加而增加。