页岩气储层含水饱和度影响因素及计算方法——以焦石坝区块五峰组—龙马溪组为例

王建波 冯明刚 严 伟 刘 帅

（中国石化勘探分公司，四川 成都 610041）

0 引言

涪陵页岩气田位于重庆市涪陵区焦石镇，构造位置位于四川盆地川东褶皱带的东南部，整体构造平缓。焦石坝地区上奥陶统五峰组—下志留统龙马溪组页岩储集物性较好，有机孔和无机孔发育，储集空间具有多样性［1］，发育大量基质孔隙和微裂缝，天然气主要以游离气和吸附气赋存于暗色页岩中，是典型的“自生自储”系统，具有顶底板条件好并且后期构造作用相对较弱的特征，属于中深层、高压的优质页岩气藏［2］。焦石坝地区页岩储层主要发育于龙马溪组龙一段和五峰组，岩石类型丰富［3-7］。由于页岩储层在黏土矿物含量、孔隙类型以及黄铁矿等方面的特殊性，地层水以复杂多样的形态存在于地层中，这增加了页岩气储层含水饱和度评价的难度。笔者在调研国内外页岩气储层含水饱和度评价相关文献的基础上，进一步研究影响页岩气储层含水饱和度的因素，并结合分析化验资料对研究区实际测井资料进行处理和评价，分析常规饱和度评价方法的适用性。

1 影响因素分析

岩石的矿物成分及表面性质、孔隙结构及孔隙比表面是影响油气饱和度的关键因素。一般而言，地层中矿物颗粒越细，孔隙结构越差，喉道越细，含水饱和度越大［8-9］。针对焦石坝地区五峰组—龙马溪组的页岩而言，黏土矿物、孔隙类型和黄铁矿是影响地层含水饱和度评价和计算的主要因素［10］。

1.1 黏土矿物的影响

黏土矿物是页岩的重要组成成分之一。根据研究区X1 井五峰组— 龙马溪组全岩X 射线衍射分析（图1a、图1b），黏土矿物随着深度增加逐渐减少，含量介于16.6%～62.8%、平均值为40.9%，以伊蒙混层（含量介于25%～85%、平均值为54%）和伊利石（含量介于12%～68%，平均值为40%）为主，绿泥石次之（含量介于1%～20%、平均值为6%）。

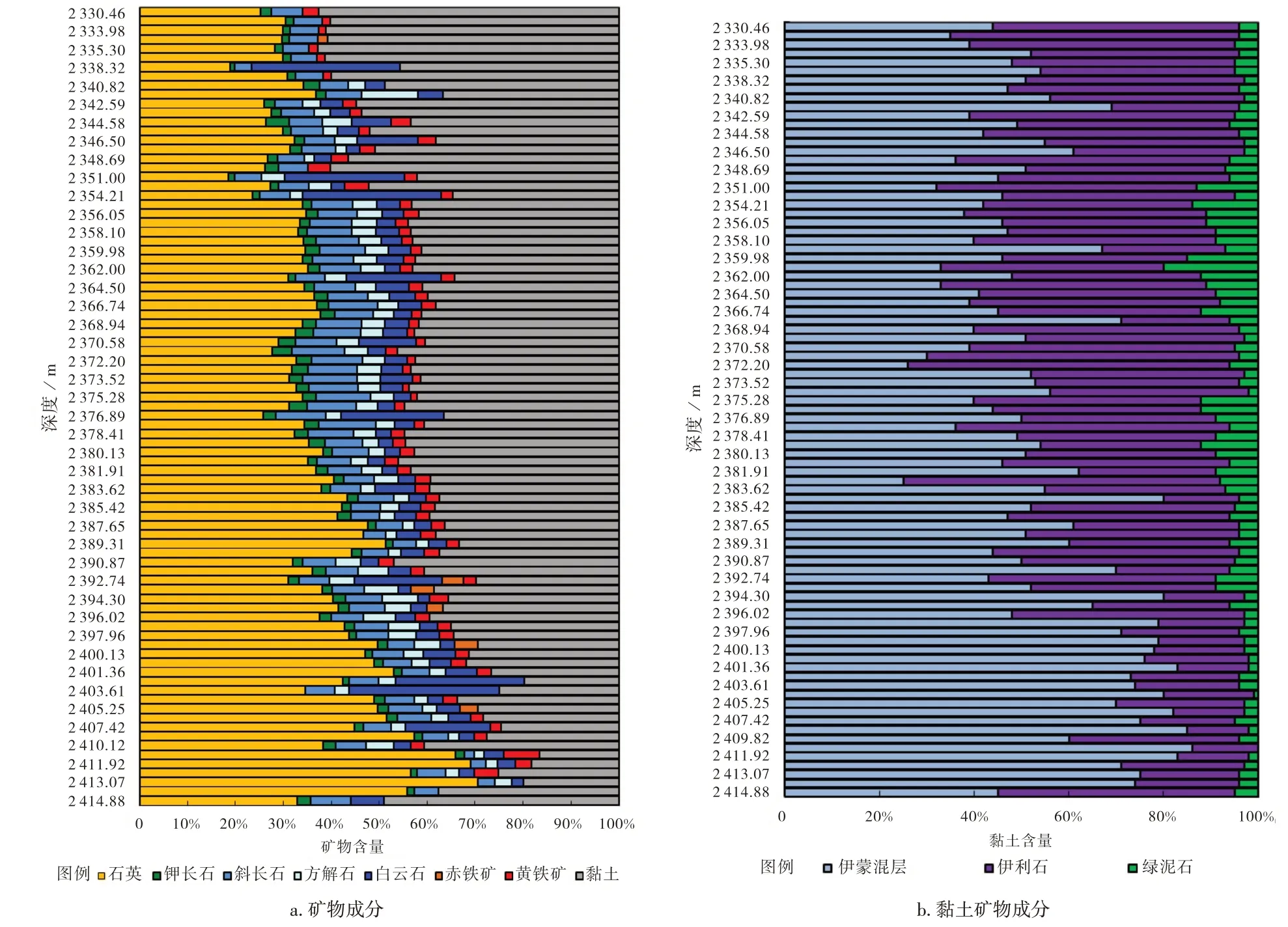
图1 X1井五峰组—龙马溪组页岩矿物成分和黏土矿物成分分布图

黏土矿物颗粒直径只有几百纳米至几微米，具有较大的比表面积和较强的表面自由能［11-12］及很强的吸附能力。伊利石和蒙脱石表面具有较强的吸水性，引起地层岩石的亲水性［8，13-14］，从而在其表面形成一种薄膜束缚水。研究区黏土矿物以伊蒙混层和伊利石为主，容易在地层岩石中形成较高的束缚水饱和度。另外，黏土矿物内部和黏土矿物之间发育一种微细的黏土矿物粒间孔和粒内孔（图2）。这类孔隙具有体积小、数量多、吸附性强的特点，在气驱水的过程中部分毛细管束缚水滞留于此类孔隙中［15-16］，所以黏土矿物孔是页岩气储层束缚水的主要赋存空间［17］（图2）。

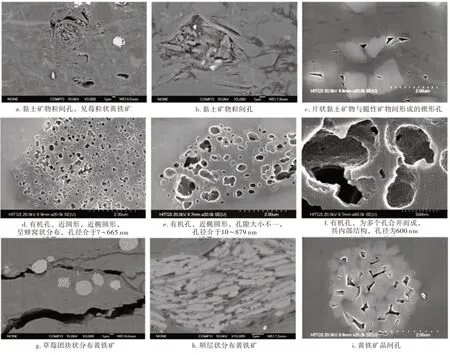
图2 各种类型孔隙及黄铁矿氩离子抛光扫描电镜照片

地层岩石的亲水性和黏土矿物孔的强吸附性导致黏土矿物表面和孔隙中优先吸附和储集水分子，对页岩气的赋存和运移有一定的阻碍作用。黏土矿物表面和孔隙中所吸附和储集的水分子通常以孔隙水、吸附水、层间水和结构水4 种形式存在［18］，除孔隙水外，其余3种水均为束缚水，使得黏土矿物含量高的地层中束缚水含量较高。这一因素会导致页岩气储层的含水饱和度比常规天然气略高。

1.2 孔隙类型的影响

应用纳米CT 扫描和氩离子束抛光扫描电子显微镜对研究区的岩样进行观察，发现岩石中存在有机质孔、黏土矿物孔、晶间孔以及次生溶蚀孔等孔隙类型，孔径介于2～300 nm。

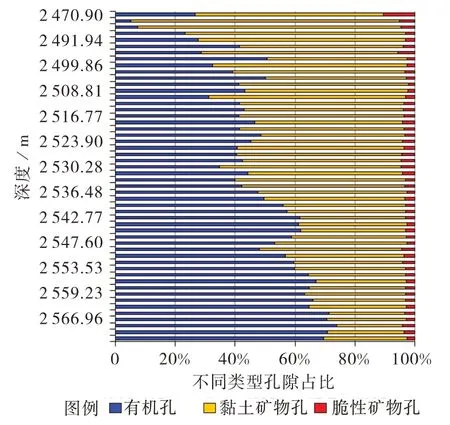
图3 X1井五峰组—龙马溪组页岩孔隙类型构成直方图

焦石坝地区X1 井五峰组— 龙马溪组页岩孔隙构成随着深度增加，从以黏土矿物孔为主逐渐演变到以有机孔为主（图3）。黏土矿物孔和有机孔占了总孔隙体积的90%以上，其他孔隙类型所占比例较少。除黏土矿物孔外，有机孔对页岩地层的含水饱和度有较大影响。有机孔是页岩中有机质在热裂解生烃过程中形成于有机质间和有机质内的孔隙，对页岩气的生成和储集具有重要意义。研究区有机质纳米孔是发育最广泛的孔隙类型之一，以微孔、中孔为主，孔径介于1.5～50.0 nm，孔隙形态为席状、片状或管状，连通性中等，喉道形态为针管状，局部呈片状、斑块状，以30 nm 中型纳米孔喉为主［19］。有机质内部纳米孔数量丰富，有机孔之间并不是孤立存在的，而是存在某种程度的连通性。在页岩生烃过程中，烃源岩中有机质生成大量的烃类分子，最终通过有机孔进入基质孔隙。部分烃类分子必须克服基质孔隙表面束缚水的阻挡，在这个过程中一些束缚水由于受到烃类分子的作用，便会突破岩石的束缚变成自由水分子进入基质孔隙中，最终通过排液过程排出储层［20］。同时，有机孔的表面具有亲油气性，该特点决定有机孔往往相对于黏土矿物孔、黄铁矿晶间孔等无机孔隙能够优先促使甲烷在其内吸附和储集，是烃类的主要储集空间［12］293。焦石坝地区五峰组—龙马溪组地层富含有机孔，形成良好的天然气导流微通道，致使地层具有较低的含水饱和度。

1.3 黄铁矿的影响

黄铁矿一般形成于强还原环境，经常与有机质和铀共生。研究区龙马溪组一段地层沉积时期为滞留、缺氧、水体较深的深水陆棚沉积环境，常见黄铁矿发育［21］，含量介于1%～8%，平均值为2%。分布形式多样，呈草莓团块状、分散状及层状分布，其中草莓状黄铁矿结核在富含有机质的页岩中较常见，内部由许多小的黄铁矿晶体组成，晶体之间存在微孔隙［22］。由于黄铁矿具有较强的导电性，表现为极低电阻，电阻率一般分布在1 × 10-1～1 × 10-6Ω · m，从而对地层含水饱和度的计算造成影响。以X4井为例（图4），层状分布的黄铁矿单层厚度一般在10 cm以下，成像图上呈黑色条带状分布，导电能力强，电阻率曲线呈明显的尖峰状下降。团块状和分散状黄铁矿多呈米粒形态，同一深度同时分布一粒到多粒，但都不是连续分布，双侧向电阻率曲线上未见明显的响应。分析认为，在地层含水饱和度较低时，黄铁矿颗粒表面的附加导电作用对储层电阻率的影响较强，且明显大于含水对电阻率的影响。但是，在近似饱含水时，少量的黄铁矿对储层电阻率的影响小于含水对电阻率的影响［23］。研究区的情况属于后者，导致计算的地层含水饱和度偏高［24-25］。所以，使用Archie 公式及其衍生公式计算地层含水饱和度时必须进行黄铁矿校正。对于近似呈层状分布的黄铁矿，采用与本深度邻近上下的主要矿物的电阻率作为真实电阻率参与计算；而对于呈分散状或草莓团块状的黄铁矿，由于其含量较低，对地层电阻率的影响较小，可以忽略其对地层含水饱和度计算的影响。

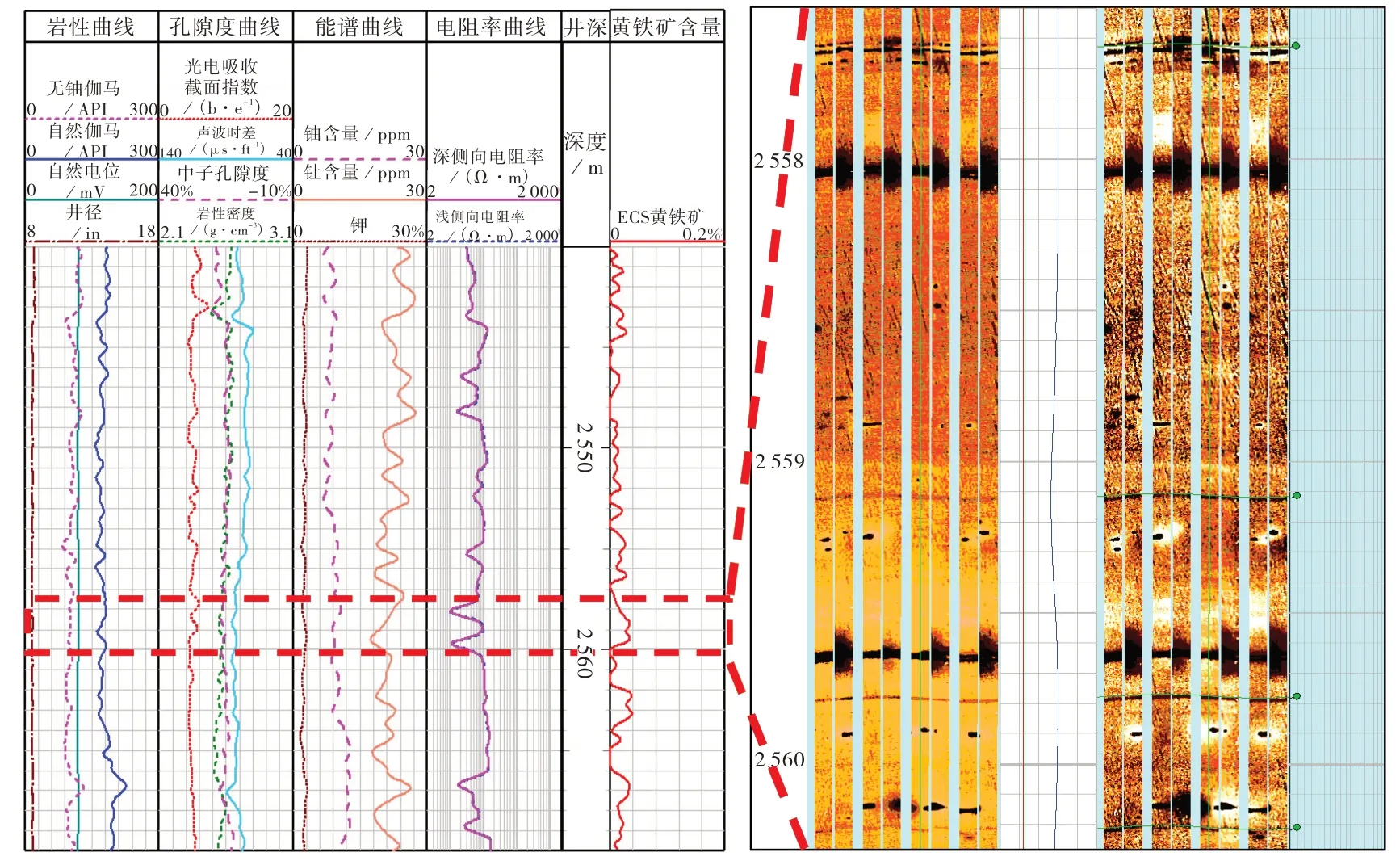
图4 X4井黄铁矿电性特征图

2 评价方法

焦石坝地区五峰组—龙马溪组页岩气储层孔隙度较高，平均值在4.0%以上，游离气含量在总含气量中占较大的比重，游离气与吸附气的比值平均为6∶4。因此对储层含水饱和度的评价提出了更高的要求，同时储层含水饱和度的计算精度将对合理评价原始气藏的游离气含量具有重要意义。笔者在明确页岩气储层含水饱和度影响因素的基础上，针对孔隙度—饱和度交会法、Archie 公式及其衍生公式等常规含水饱和度评价方法的应用条件和适用性进行了分析。

2.1 孔隙度—饱和度交会法

在同一个气藏系统中，针对均质性孔隙型储层，位于气水界面之上的流体满足毛细管力作用原理，其束缚流体饱和度与孔隙度的乘积趋于常数，即孔隙度与饱和度具有明显的单边双曲线规律。

根据焦石坝地区X4 井封蜡岩心实测的原始含水饱和度和孔隙度进行二者的双曲线相关性分析（图5），建立岩心分析孔隙度与含水饱和度之间的关系式：

式中，Sw为含水饱和度，%；∅为岩心分析孔隙度，%。

通过式（1）计算得到含水饱和度，计算结果如图6所示。

2.2 Archie公式及其衍生公式

2.2.1 Archie公式

图5 X4井封蜡岩心实测孔隙度与含水饱和度关系图

Archie公式通过对大量砂岩样品进行测量，首次提出了测井解释中两个最基本的参数和两个最基本的解释关系式，从而形成经典的Archie公式［26］：

式中，Rw为地层水电阻率，取值为0.046 Ω · m；Rt为地层电阻率，Ω·m；a 为岩性系数；m 为孔隙度胶结指数；b为饱和指数；n为饱和度指数。

对X2 井五峰组—龙马溪组11 块岩样进行岩心地层因素F 和电阻率增大系数I 测量，通过F-∅、I-Sw关系拟合确定岩电参数a为1.05、m为1.53、b为1.01、n为1.93。

2.2.2 Simandoux公式

Simandoux 公式是基于均匀分布的黏土混合泥质砂岩建立的，将泥质岩石的导电性看成是泥质和纯岩石两部分并联导电的结果，认为泥质以黏土混合物的形式均匀分布在地层中［27］，如式3所示：

图6 X4井测井计算与岩心分析含水饱和度对比图

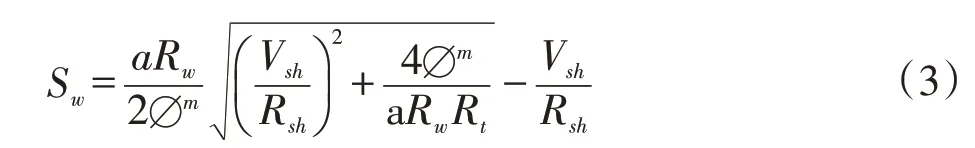
式中，Rsh为页岩电阻率，Ω·m；Vsh为黏土含量，%。

根据研究区五峰组—龙马溪组地层特点，Rsh取值为15 Ω ·m，Vsh通过常规测井解释获得，最终得到黏土校正后的含水饱和度。

2.2.3 Total Shale公式

Total Shale 公式是斯伦贝谢公司在Simandoux 公式的基础上进行改进后的模型［28］，如式4所示：

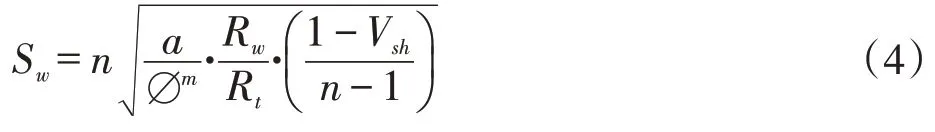
在Simandoux 公式的基础上，Total Shale 公式考虑了饱和度指数n，并在纯砂岩项中去除了泥质体积的影响，提高了饱和度计算精度。

2.2.4 实例分析

利用X4 井的封蜡样岩心分析结果，对上述4 种方法得到的饱和度值进行刻度，计算的含水饱和度存在明显差异（图6），最大处计算结果相差20%。通过对4 种方法的对比，孔隙度—饱和度交会法得到的含水饱和度最高，Archie 公式次之，Simandoux 公式计算的含水饱和度更低，Total Shale 公式最低。这4种方法计算的含水饱和度变化趋势与岩心分析结果基本一致，随着深度增加含水饱和度越来越低。

利用孔隙度—饱和度交会法计算地层含水饱和度存在如下局限：①实验室分析的岩心饱和度样品为封蜡样，不是密闭取心样，其岩心分析的含水饱和度并不能完全代表气藏地层的原始含水饱和度，影响含水饱和度的测量精度，导致孔隙度与饱和度之间的相关性变差；②样品的孔隙度分布范围较小，介于4%～7%，缺少低孔隙度（孔隙度小于4.0%）和高孔隙度（孔隙度大于7%）储层段的样品，导致孔隙度与饱和度之间的单边双曲线规律代表性不够，从而影响地层含水饱和度的计算精度。

同样，利用Archie 公式及其衍生公式估算地层含水饱和度均存在各自的局限性：①Archie 公式中充分考虑了a、m、b、n 等岩电参数；而Simandoux公式中认为泥质含量多的油气层n 值取2.0，焦石坝地区五峰组—龙马溪组页岩地层n 值为1.93，存在一定的差异，对计算结果将产生影响；Total Shale 公式在Simandoux 公式的基础上考虑了饱和度指数n 的影响［29］，提高了计算精度。②Archie 公式是在对大量纯砂岩样品进行实验的基础上得到的地层含水饱和度计算模型。虽然焦石坝地区黏土含量较高，但多为分散状，少有呈层状泥质，可近似认为地层的导电性仍具有较好的均质串联导电特征，利用Archie公式计算地层含水饱和度有较好的适用性；而Simandoux公式和Total Shale公式虽然考虑了黏土含量的影响，但是泥质与纯岩石并联导电的模型与研究区的实际情况存在差异。

3 结论与建议

1）页岩地层储集空间具有多样性，含水饱和度影响因素较多：地层中黏土矿物含量高，黏土矿物孔中赋存部分束缚水；有机孔大量发育，连通性好，孔隙表面具有亲油气性；黄铁矿颗粒表面具有附加导电作用，从而影响电阻率测井。以上因素均影响对页岩地层含水饱和度的准确评价。

2）焦石坝地区五峰组— 龙马溪组储层孔隙类型构成变化较大，随着深度增加有机孔所占比例增加，黏土矿物孔减少，含水饱和度逐渐减小。

3）对页岩地层的含水饱和度进行评价时必须充分考虑黄铁矿和黏土矿物的影响。多种方法计算得到的结果与岩心分析结果的变化趋势基本一致。针对焦石坝地区页岩地层均质性强、纵向变化小的特点，采用Archie公式计算含水饱和度效果较好。