追问数学概念的前世今生提高教学设计价值
邱莹
四川省成都市武侯区教育科学发展研究院,四川成都 610041
概念教学是数学课堂教学中的一个重要内容,也是多种新授课型中最难于把握的课型之一。概念的建立不能仅停留在熟记背诵概念的层面上,学生学习一个概念一般要经历感知、建构、理解、内化的过程,最终才能形成概念[1]。在《分数的再认识》一课教学设计过程中,笔者感受到了来自数学概念课的层层拷问和冲击,对概念课的教学设计也有了一些新的感悟。因此笔者通过以下几个步骤的实施来充实对《分数的再认识》这个教学内容的理解。
1 厘清概念,了解数学文化
在进行概念课教学设计前,最好先查阅资料,以便对概念能有更深入完整的认识。了解概念的内涵及外延,以便在教学过程中抓准概念本身,厘清概念的内涵和外延,才能在教学过程中丰富概念的内涵,建构概念的外延。
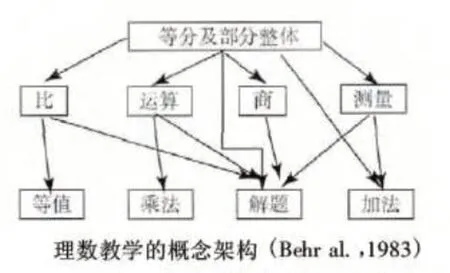
1.1 分数的意义
分数主要表达了整体与部分之间的关系,其意义可以从4个方面来理解和建构(如图)[2]。
1.2 分数的起源
分数一词来自拉丁文的"frangere",意义是指分开,通常用来描述一个被分开的全体之部分。分数的发明最初即是为了因应各种测量上的需要[2],在三千多年前的古埃及,为了在不能分得整数的情况下,发明了分数,由于符号的限制,古埃及的分数只有这样的分子为1的分数,也就是说一开始人类发明的就是平均分后的一个计量标准——分数单位。如果需要表示,则会写成的形式。因此分数在测量上的意义也是分数意义的一个重要体现方面,在认识分数单位时,应该有所体现,北师大版的教材也是从小纸条测量数学书,不够测,需要找到更小的标准,来引出分数单位的,这一点和分数的起源、分数单位的产生是契合的。
1.3 分数与小数
既然分数和小数能互化,有了小数为什么还要发明分数呢?原因有二:一方面分数出现的时间比小数早,小数的雏形是公元三世纪我国古代数学家刘辉为了解决一个数学难题时提出的微数,而正式提出小数的名称已经是公元十三世纪了,因此虽然北师大版小学数学教材中的安排是先学习小数再学习分数,但是实际上确实是分数先产生,小数后产生。教材的安排也有它的道理,小数的运用在生活中更加常见,生活经验能正向迁移到小数学习;且小数的位值、数位、计数单位都可以完全参照整数来学习,因此教材安排先学习小数。另一方面,分数出了可以表示一个数量,还可以表示整体与部分之间的关系,还可以表示除法的过程,也能表示运算结果,分数与小数相比内涵更加丰富,具有多重意义,并且分数的数域更加宽广。
2 学段纵向对比
分数的认识是小学阶段数的认识中的一个重要内容。小学阶段对20以内、100以内、万以内、及亿以内的整数进行了认识,实现了数级的拓展。而负数的认识,作为表达相反意义的量,实现了数轴自右向左地反方向扩张。小数、分数及百分数的认识则是由“整”到“不整”,实现了由宏观向微观的数域的拓展。作为后续学习分数运算、分数小数互化、解决简单实际问题、百分数、比等相关知识的重要基础,也是初中对实数、有理数认识的重要基础,厘清分数的概念显得尤为重要。《分数的再认识》,其中这个“再”字,意指三年级已在感性上初步认识了分数。对比三年级和五年级的教材发现:
2.1 单位“1”发生了变化
三年级时认识了分数各部分的名称和分数的读写法,也初步了解了“整体”是一个物体,或多个物体的分数。五年级则对单位“1”进行了进一步的丰富,一个物体(可以补充一条线段或计量单位)、一组物体、几组物体都可以合起来看作一个整体,数的清的物体、数不清的物体、甚至未知个数的物体,都可一看作一个整体,成为单位“1”。
2.2 分数的定义发生了改变
2.3 分数表达了整体与部分之间的关系
三年级已经对分数整体与部分之间的关系有了感性上的认识,但一般停留在分数表象上的认识,也就是单纯从数量上考虑,也就是整体是几,分母就是几,部分量是几,分子就是几。也有孩子能够达到理解份数的层面,五年级的再认识则从数量上升到了份数的考虑,也就是整体是几份分母就是几,部分量是几份分子就是几,而更多地内涵则是指向了分子分母之间的关系。
3 着眼于学生知识的起点
学生在三年级时已学过分数的初步认识,会比简单分数的大小比较,能进行简单的同分母加减法计算,并解决实际问题。学习分数的再认识到底该学习什么,又怎样激发孩子的兴趣和对知识本源的追求呢?带着问题,笔者进行了关于分数的一次调查问卷。为了保证数据的真实性,能反映现实问题,对还未学习《分数的再认识》一课的五年级学生做了无准备调查(学生不知情,未提前查阅资料或复习),时隔1年有余,孩子的回答也是很具分析的价值。
调查对象:五年级49名学生,整班包括各个层次的学生
调查方式:无准备调查
调查结果分析:
问题1:关于分数你已经知道了什么?
有53.06%的孩子印象最深刻的是分子分母分数线等分数的表象,对于分数的初步认识的其他知识孩子能回忆起来的就不多了。但是可喜的是也有24.49%的孩子在对分数的意义做积极的思考:分子分母表示的是什么,分数的作用,分数可以表示数量,证明孩子在初步学习的时候都在对分数的意义做有益地尝试。另一方面提及平均分的孩子非常地少,只占了8.16%,分数是建立在等分的基础上的,没有平均分,何谈分数?本以为孩子会对平均分认识深刻,可事实并非如此,因此在复习旧知的时候,需要特别提谈一下平均分,突出平均分的重要性。
问题2:关于分数你还想知道了什么?
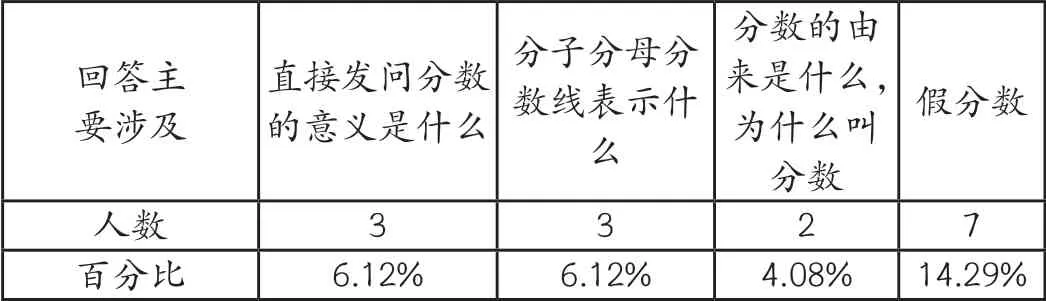
回答主要涉及直接发问分数的意义是什么分子分母分数线表示什么分数的由来是什么,为什么叫分数假分数人数3 3 2 7百分比6.12%6.12%4.08%14.29%
答案组成如下:看到了孩子这么多稀奇古怪,又充满思考的问题,突然觉得一些我们的预设,真是主观臆断,上课不也应该由孩子的实际需求出发,去用自己的认识碰撞敲打他们的认知吗。
在受访学生中,只有6.12%的学生明确提及平均分。而有意思的是有55.10%的孩子选择了以4个相同的物体作为单位“1”,借助它天然平均分的属性,来界定平均分。看来在三年级的学习中等分观念确实有建立的,但覆盖面积还不够广,且无法明确表达出来,所以孩子就只能借助其他途径来表达。
有62.22%的学生可以正确完成,并说明理由。33.33%的学生是完成错误。看来孩子对数量的认识远大于对份数的认识,并且对分子分母表达的意义不是很明确。那么我们在教学过程中就应该关注分数表示整体与部分之间的关系,以及分子和分母表达的含义。
4 教学中遇到实际的困难
在学习过程中,我们发现,由于有了前知的铺垫,孩子要抽象出分数的意义那句话是不太难的,但是能概括出这句话,就能理解分数的意义吗?比如分数的概念,表述为“其中的一份或几份”,那么在理解为什么会出现假分数时,就会出现问题:明明是拿单位“1”来分的,分数怎么可能比单位1还大呢?如果借鉴人教版教材改成“表示这样的1份或几份”,就能从文字上规避这个尴尬问题的发生。但学生对先分后取的困惑依然是存在的,因此在教学时要落实分数是表示整体与部分之间的关系。
五、关于整节课的结构安排
一般讲授概念课时,教师都喜欢抠字眼,将每一个词语抠清楚了,再连接成了一个完整的概念(如左图)。这样的教学设计方式缺乏对概念的整体建构。

为了对概念深刻理解及灵活运用,笔者将整节课的结构安排做了一个调整(如右图):首先基于学生的感性认知不断累积,抽象出分数的概念,再通过教学环节的设置来回扣分数的意义,体会分数表示整体与部分间的关系。
5 结语
通过这次深度研读教材和分析学生的经历,看待问题的深度广度都发生了变化。希望为今后的研究提供有效的研究途径,为做概念教学课提供一个具有实操性的研究范式。坚持追问数学概念的前世今生,一定提升教学设计的价值。

