基于最小二乘法的场景重构目标车辆预测算法
刘卫东, 罗华平, 王爱春, 黄少堂
(江铃汽车股份有限公司, 江西 南昌 330001)
可预期的未来十余年,高级驾驶员辅助系统ADAS和无人驾驶将是汽车行业最具创新性和颠覆性的前行方向。精准、直观、智能的场景重构,是前者演化的重要组成部分,并为持续丰富的行驾体验提供支撑。
目前而言,传感器(雷达、摄像头等) 由于自身感知能力的局限性,无法保证全天候有效地提供真实的外部环境数据,如,因自车颠簸,造成传感器视场角偏转,从而丢失前车目标。基于此情形的场景重构,必会出现目标车辆在仪表/显示屏上短暂消失,干扰驾驶员判断,影响驾驶体验,更严重者导致安全事故。
本文基于某公司的中距离毫米波雷达 (MRR) 感知&探测方案,以最小二乘法为核心,考量正常道路行驶的场景进行条件约束,设计出一种简洁、高效的追踪&预测算法,旨在持续、稳定地追踪目标,从而支撑场景重构中目标车辆可靠、有效的显示,达到最优行车体验。
1 最小二乘法介绍
最小二乘法(又称最小平方法) 一般形式可如下式:

观测值就是通过实验或者测量得到的多组样本,理论值就是假设的拟合函数。最小二乘法核心思想是求解未知参数,使得理论值与观测值之差 (残差) 的平方和 (损失函数) 达到最小,此时拟合函数的曲线可最大精准地反映观测值的基本趋势。由高斯-马尔可夫定理可证明,在给定经典线性回归的假定下,最小二乘估计量是具有最小方差的线性无偏估计量。
基于上述,最小二乘法已成为目标追踪&预测的常用方法之一,其相比于卡尔曼滤波、α-β-γ滤波等方法,原理简单,易于编程实现,在一定条件下具有良好的统计性,更具有工程实现意义。
在现实中,物体的运动轨迹按一定规律随时间变化,假定在N个顺序时刻的观测值为f(ti)(i=1,2,…,N),满足与之残差平方和 (损失函数) 最小二乘多项式 (拟合函数)p(t)的系数为a0,a1,…,am(m 通过S对ak求偏导数,令偏导数为0,可得到多项式的系数通解: 事实上,如用矩阵求解,推导出的多项式系数通解公式更为简洁和易理解,简述如下。 将N点前观测值和假设多项式组成超定方程组: 式中:αj(j=0,1,2…m)为多项式系数;Tij(i=1,2,3…N;j=0,1,2…m)为自变量t在i顺序时刻的j次方;Yi(i=1,2,3…N)为在i顺序时刻的观测值。 对式(4) 向量化后为: 因超定方程组固有特征,通常无解,需寻找最合适的α,让方程组“尽可能”成立,由此引入损失函数S: 如果矩阵TTT非奇异,则αˆ有唯一解,即多项式系数通解 本文所选择传感器是某公司第4代通用中距离毫米波雷达,探测感知范围:纵向最大有效距离120m,横向最大有效距离左右各10m。通过CAN总线,以20ms为周期,上报位于传感器左前、前、前前、右前方位,共4个目标车辆相对于传感器的纵向(Dx) 距离和横向(Dy) 距离。 基于实际正常行车场景,可作以下设定。 1) 在正常行车过程中,所有的目标车辆,都可视为在以传感器或者本车为原点的二维平面内,沿X正轴 (纵向)和Y轴(横向) 连续(性线) 运动。 2) 在较短的时间段内,可视为目标车辆相对自车作匀速直线运动。 由上,目标车辆与本车的距离变化可等效为一次函数: 式中:D——在第N个顺序时刻目标车辆相对于本车的位置;D0——开始观测时目标车辆相对于本车的初始位置;v——目标车辆相对本车的速度;T——从开始观测到N个顺序时刻的持续时间。 1) 本车和目标车辆运动变化是相互独立的,为保证运动模型有效,本算法在实现中,只对最近6组测量数据(N=6),即100ms时间段内进行一次函数(拟合函数) 求解,可得: 可测量或已知,由矩阵解可得: 2) 为保证预测准确性,当目标丢失时,基于式 (10)和式(12) 的结果αˆ,仅计算(预测) 不超过500ms的目标运动轨迹,预测时间达到设定阀值(如500ms),将对目标停止预测。 3) 本算法仅预测目标车辆的纵向距离,并设定纵向预测的有效范围[DXNEthr,DXFEthr](如近端DXNEthr=10m,远端DXFEthr=100m)。当预测距离不在设定范围内时,可认为目标永久丢失,将对目标停止预测。 4) 本算法不对目标车辆的横向距离预测,仅对最近6组横向测量数据进行加权平均wi+1>0,且wi为正整数。当目标丢失时,判断DYmean是否在有效范围内,如不在,可认为目标车辆驶离本车道,即目标永久丢失。基于实现行车场景,需预设两类有效范围值,分别适用于左&右目标,前&前前目标。 5) 因实际道路行驶场景,目标车辆相对本车通常最大速度为240km/h (约66.67m/s),即两车以120km/h相对而行,进而可得一个报文周期 (20ms),两车最大位移距离约为1.3m。由此可认定:当最近两组测量数据Dt-1,Dt之差绝对值|Dt-Dt-1|>ΔD (本算法设定为ΔD=4m) 时,追踪的目标已切换,从而需重新求解一次函数 (拟合函数),以匹配新目标的运动轨迹。 图1 算法基本流程图 本算法经实际道路行车测试,可取得预期效果。如图2所示,在两车相对速度约为40m/s情况下,目标车辆丢失500ms (1.32~1.82s;51.31~67.95m),通过拟合函数计算(预测) 的目标车辆位置和真实位置仅相差约4m,已满足在场景重构中,平滑地示意目标车辆位置。 图2 实际道路行车测试 本文所介绍以最小二乘法为核心的目标车辆预测算法,原理易懂,计算量小,编程简单,可很好地实现目标车辆平滑地动态显示,提升和丰富行车体验。由于最小二乘法固有特征,在机动性很强的系统中,很难保证对目标的稳定跟踪,因此不适合于对目标车辆长时间预测,从而导致误差偏大,失去应用的意义。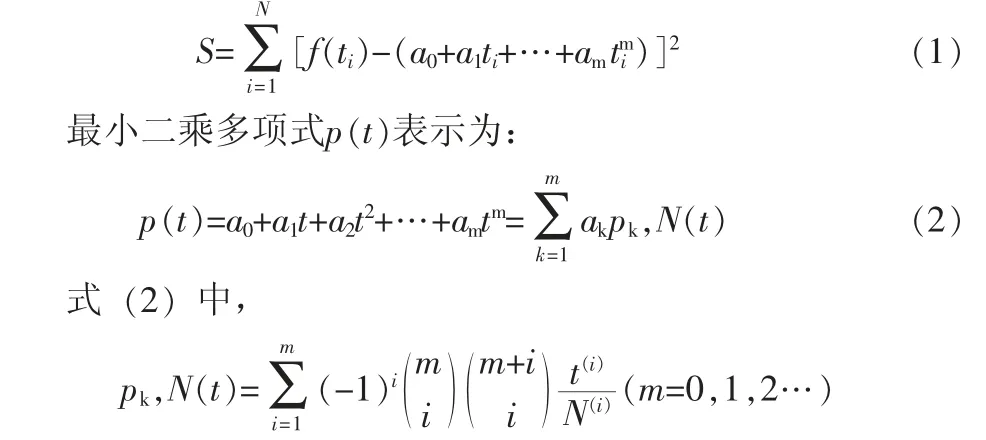

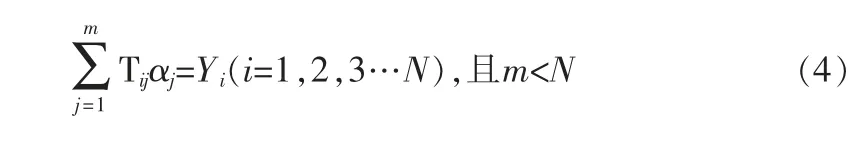



2 算法实现
2.1 感知&探测方案简介
2.2 运动模型建立

2.3 算法详解
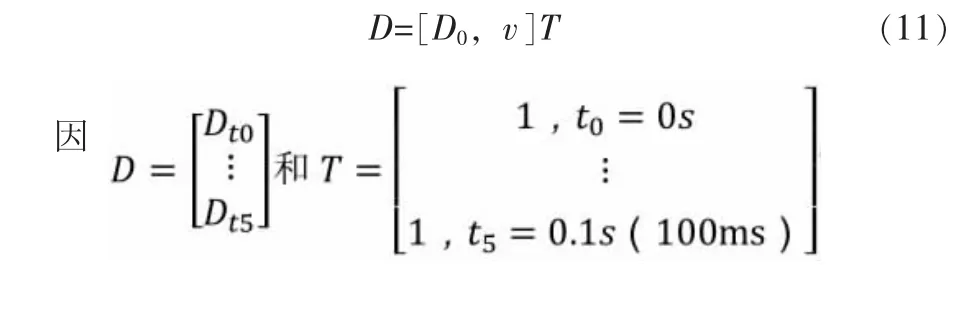

2.4 算法基本流程图(图1)

2.5 算法验证

3 总结

