“课程思政”理念指导下的贝叶斯公式教学1

李广玉，田 研

（无锡太湖学院 基础课教学部，江苏 无锡 214000）

“课程思政”的核心思想就是要从高等教育的育人本质出发，从国家意识形态战略高度出发，抓住课程这个载体，充分发挥课堂教学在育人中主渠道作用，着力将教书育人落实于课堂教学的主渠道中.“课程思政”理念下的大学数学教学，不仅让学生能用数学来分析问题、解决问题，更重要的是挖掘数学知识背后的育人功能.“课程思政”理念是始终贯穿课程的，但是要根据实际情况进行设计，不是每个教学内容都适合融入，对于可以开展“课程思政”的课堂也不一定都浓墨重彩，而应详略得当.恰到好处的引发思考就好，每一堂课都进行“课程思政”容易产生疲劳厌烦情绪.因此，有时可进行课程内容相关的“课程思政”，有时只是学习方法、态度、时间管理方面的，有时是课后进行的.总之，“课程思政”要讲时机、讲方法，贝叶斯公式非常适合进行“课程思政”教学内容.贝叶斯公式的引入方式通常有以下几种：其一，复习条件概率，乘法公式和全概率公式，然后启发引导出贝叶斯公式［1］.其二，通过简单实例，引入贝叶斯公式，如摸出红色球，问是哪个箱子的，或者是出现次品问是哪个工厂生产的传统题目［2］.其三，以趣味性、知识性、应用性等角度引入、阐述贝叶斯公式［3］.纵观文献资料，未见到从“课程思政”角度进行的课程设计.

1 贝叶斯公式教学设计背景及思路

贝叶斯公式是《概率论与数理统计》课程的教学内容，通常是在《高等数学》后大二开设的课程，此时学生已适应大学生活，初步的大学计划目标已确定，生活进入正轨，除了正常的学习和社团活动外，大学生谈恋爱现象越来越普遍，恋爱观是人生价值观的重要组成部分，如果能引导学生追求爱情的同时注重提升自己，将更好的自己呈现出来.当学生有更高的追求目标，能更理性看待恋爱时，就不容易被不良思潮影响，能在恋爱生活中勇敢而谦恭，自制而真诚.用贝叶斯公式去理性的分析恋爱，是一个自我审视的过程，可以帮助找到自己的不足，提升获得幸福恋爱的概率，进而转向工作就业的问题上，面对心仪的公司，如何能更好的争取到理想的工作岗位，一样需要查缺补漏，弥补自己的短板，从而提高竞争力以更大的概率去获得职位，更进一步，工作关系中如果遇到“众口烁金”的情况又该如何看待？可见，“课程思政”理念指导下的贝叶斯公式教学是全方位从恋爱、工作、生活方面进行积极的引导.课程最后讲一个传统的假阳性问题，加深贝叶斯公式的理解及应用，然后拓展贝叶斯公式的用途.

2 贝叶斯公式教学实践

引例：恋爱表白失败什么原因？怎么办？上次课我们学习了全概率公式，可以简单看成“由原因推结果”的概率求解方法，有同学回去后做了一个大胆的恋爱尝试，他把恋爱目标通常最看重的三个方面作为一个完备组，设A1={相貌}，A2={品行}，A3={家境}，并且主观赋予概率分别为1/4，1/2，1/4，再设B={恋爱表白成功}，根据经验设

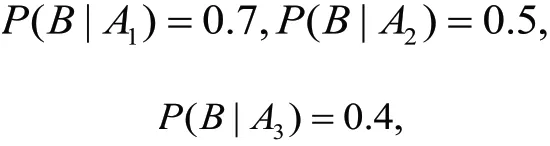
然后利用全概率公式，计算出恋爱表白的概率为

概率虽然不高，但是超过一半，于是采取行动去表白，结果表白失败，问我什么原因？怎么办？我们来帮他分析.

品行方面的原因所占概率较大，上面的公式就是贝叶斯公式，只需用到条件概率、乘法公式和全概率公式，分母是全概率公式，分子是分母的一部分.此时可给出贝叶斯公式完整的严格的叙述，已知结果，求产生结果的原因概率，可帮助寻找产生结果的最可能原因.然后回到第二个问题上，表白失败了怎么办？从贝叶斯公式的结果出发，当然是想办法提升自己的品行方面，也就是提高自身修养，做有责任心、善良、追求上进的青年，展现出大学生的精神等，使概率增加，当然还可以从相貌上注意，改善自己的仪表、气质、谈吐，或者从自己的工作就业方面改善家境情况.就业也一样，对于自己心仪的公司，理想的职位，对照用人单位的专业、敬业、忠诚度等标准，逐步改进自己，就可以更大概率接近自己的工作目标.这个例题容易理解，而且同学一定印象深刻，会自动复习，引例所解决的问题是“由结果推原因”的概率计算方法，引导学生为了达到理想的恋爱、工作目标，需要不断完善和提高自己，才会匹配更好的，可以起到一种激励作用.接下来用贝叶斯公式解释生活谚语，拓展学生思维，了解生活中的智慧.

例1：生活中你有没有过这样的经历：不被身边的人理解，受人排挤，但是深信自己的对的，真理掌握在少数人手中的感觉，比如寝室的同学或者班级的同学，认为你有点不合群，有点格格不入，而你觉得是“别人笑我太痴癫，我笑别人看不穿”这样的过程是复杂的，有点痛苦的，因为“三人成虎，人言可畏”.

假设事件A 本身可信的概率为0.2，现有10 个人，相互独立，若每人说谎的概率为0.4，传到第十个人时，认为事件A可信度是多少呢？

解：记 Ai={第i个人说A可信}，（i=1，2，…10），

则

利用贝叶斯公式，当在第一个人说A可信后，A的可信度可修正为

当第2个人说A可信后，A的可信度又进一步修正为

以此类推，当第10个人说A可信后，A的可信度又进一步修正为0.9351，接近于1，也说明这10个人很有可能都说了真话，A 确实是可信的［4］.但是不要忘记前提条件是假设10个人相互独立的.通常所遇到的情况往往相反，一般都是周围有某些利益关系，或者共同目的相近心理的人，并可不是独立的，而是众口同声，不要被吓倒，要坚持自己的信念，不违背意愿，不降低节操，不妥协于不正之风，相信公道自在人心.要判断众人说的真假，关键看评论的人是否相互独立，要理性分析，辨别真假，做个有智慧的人.如果学生感兴趣还可以讨论一个例子，为什么找工作的时候要笔试、面试，面试还可能有一面、二面，其实也是个逐步判定你是否真的适合这份工作的过程.

例2：（假阳性问题）某地区患有癌症的人占0.005，患者对一种试验反应是阳性的概率为0.95，正常人对这种试验反应是阴性的概率为0.98，现抽查一人，试验反应是阳性，问此人是癌症患者的概率有多大?

解：记A1={抽查的人患有癌症}，A2={抽查的人没有癌症}，B={实验结果是阳性}，可画概率树图来帮助分析（见图1），理清关系.

图1 概率树图

用贝叶斯公式计算的结果为0.1 927，概率很小，那么这种试验对于诊断一个人是否患有癌症有无意义？检出阳性是否一定患有癌症?当然是有意义的，因为0.1927÷0.005=38.54，说明提高了38倍.但是检出阳性不一定患有癌症，这要求理性分析，通过复查就可以进一步确定，此时P(A1) =0.1927，重复上面的算法，新的

可见，复查呈阳性，那么基本可以确诊为患有这种癌症.原来的P(A1|B)小的原因是P(A1) =0.005太小，因为

可看出为什么人们喜欢找有经验的医生.所谓“假阳性”，即阳性结果完全不足以说明病人得病.其实医院在确诊前不会只做一种或一次检查，还会辅以其他指标，如心电图、脑CT、胸透等，有时结合计算机综合诊疗.

以上例子都是加强原有结果即先验概率，事实上，也可以减弱先验概率，比如“狼来了”故事，以及贝叶斯本人的生平事迹等.后来的学者依据贝叶斯公式的思想发展了一整套统计推断方法，叫“贝叶斯”统计，它建立在主观判断的基础上，可以不需要客观证据，先估计一个值，然后根据实际结果不断修正.可见贝叶斯公式的影响，它已在疾病诊断、安全监控、质量控制、安全部门的招募、药剂检测等方面发挥着重要作用.

综上，“课程思政”需要逐步开展，进行贝叶斯公式这样的专题研究，充分发挥和体现课程的育人功能和教师的育人责任.“课程思政”的有效进行，还需提升教师的德育意识和能力及自身的德育水平，这样才能融会贯通，否则例子用不好会显得牵强，甚至错误.