不确定性时变时滞奇异摄动控制系统的输出反馈控制器设计

王永超

（吉林师范大学 数学学院, 吉林 长春 130000）

奇异摄动系统在现实工程系统中经常遇到[1]. 时滞和不确定性的存在往往使得控制系统达不到满意的性能指标甚至不能保证控制系统的稳定性,近几年，众多学者关注对不确定性时滞奇异摄动控制系统的研究,并取得了一些成果[2-4].

本文通过构造适当的Lyapunov 泛函，结合Schur 补引理和线性矩阵不等式等方法, 讨论了不确定性时变时滞奇异摄动控制系统的控制器设计问题, 给出了输出反馈控制器的设计方法.

1 预备知识

考虑如下不确定性时变时滞奇异摄动系统[5]:

其中,τ 、 μ 是已知的常数; φ （t）是连续向量初始值函数. F （t） ∈Ri×j是具有勒贝格(Lebesgue)可测元的适当维数的不确定实矩阵, 其不确定性满足范数有界条件:

欲设计系统(1)的输出反馈控制器如下:

其中, K 是待定的适当维数的控制器增益矩阵, 则相应的闭环系统为:

引理1[6]如果存在矩阵 Zi（i= 1,2, …,5）且, 满足下列LMI 条件:

则

其中

引理2[6]给定和对称矩阵 S1、 S2、 S3, 如果以下条件

成立, 则

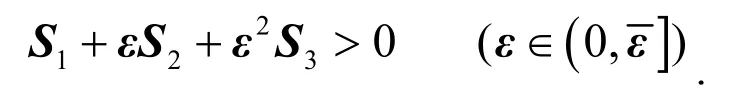
引理3[7]给定适当维数的矩阵E、D, 对称矩阵Y , 不确定性矩阵 F （t）满足 FT（t） F （t）≤ I, 所以

的充要条件是: 存在正常数η ＞0 , 使得

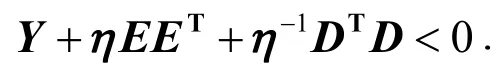
2 主要内容

定理1给定常数＞0,若存在对称正定矩阵Q＞0, 适当维数矩阵, V 以及矩阵 Zi（i =1, 2, … ,5）且,满足下列LMIs 条件:, 那么存在静态输出反馈控制律,, 使闭环系统(1)是渐近稳定的.

证明拟选取如下Lyapunov-Krasovskii 泛函：

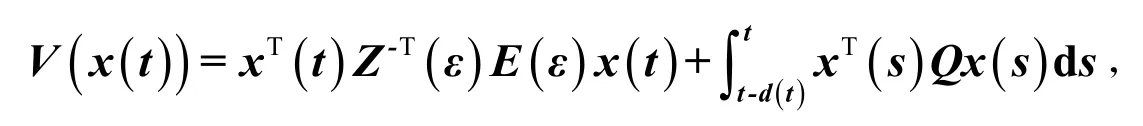
其中，Q＞0, 是待定的对称正定矩阵.

由引理1 及LMIs 条件(4)、(5)和(6)，可得

则

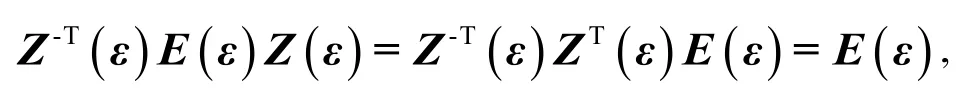
故

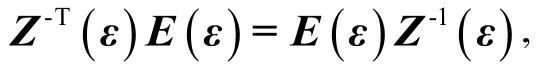
可知矩阵 E （ε） Z （ε）是正定的, 从而推出Lyapunov-Krasovskii 泛函 V （x （t））是正定的.

沿闭环系统(3)的任意轨迹进行微分, 得

其中

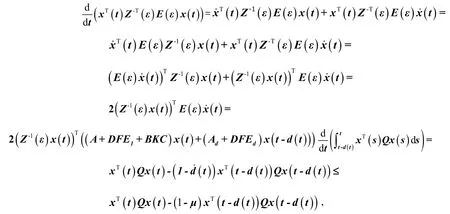
所以

其中，

显然, 矩阵不等式（9）对变量K, Q 和 Z （ε）是非线性的. 定理1 给出控制器存在的充分条件, 为了求得控制器参数, 需要去掉矩阵不等式(9)中的不确定性函数 F （t）.

令

则

由引理3 可知:存在唯一标量η ＞0 , 满足:

利用Schur 补引理, 得

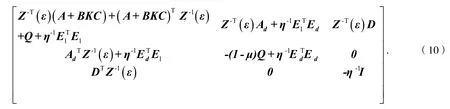
再由Schur 补引理, 式（11）等价于

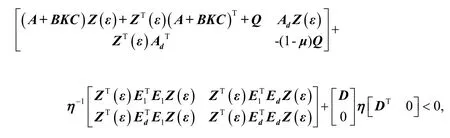
即

定义

则

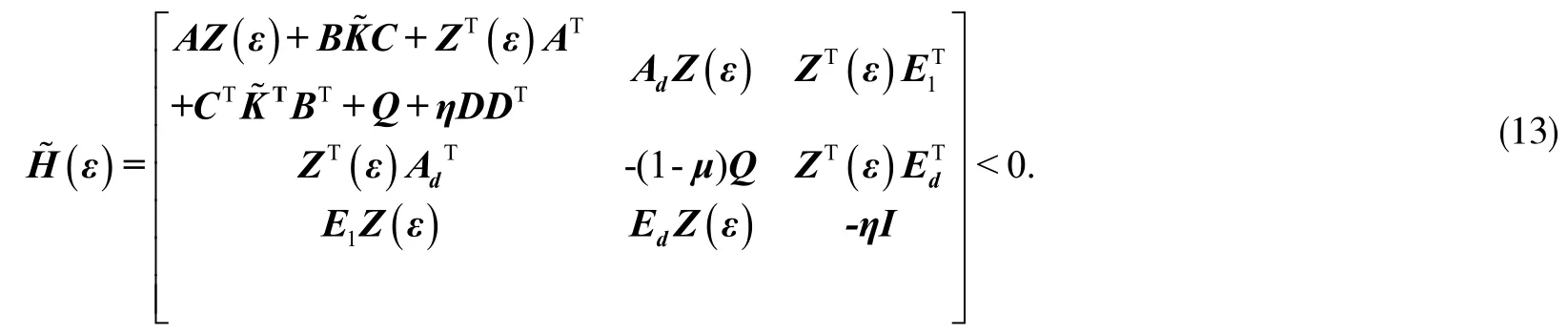
故可知

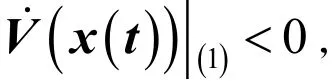
即u （t） = Ky （t）是系统(1)的输出反馈控制律, 又由条件(12), 可得

证毕.

3 结论

为了解决不确定性时滞奇异摄动控制系统的输出反馈控制问题，通过LMI 和Lyapunov 泛函相结合给出了一种新的方法，最终得到了闭环系统渐近稳定的充分条件及相应的输出反馈控制律.