多元凸函数连续性的2 种证明
唐建国,叶桂余
(惠州学院 数学与统计学院,广东 惠州 516007)
一元函数的凸性是研究函数曲线形状的重要工具.数学分析教材给出了一元凸函数不带连续条件的定义、一些等价条件和凸函数的判定方法,但对于凸函数的连续性问题,现行教材在定义和性质中均未涉及[1-2].部分学者研究一元凸函数的连续性问题,如:证明了一元凸函数的有界性和连续性[3-5];探讨了闭区间上凸函数在区间端点的连续性问题[6];给出一元凸函数的一个与上半连续性相结合的等价定义[7];讨论了一元凸函数的连续性和有界性,定义了扩充单调的概念,以此为基础给出了开区间内和闭区间内凸函数的扩充单调性质[8];从一元凸函数的定义出发,讨论了凸函数与连续的关系[9];分析比较了一元凸函数的弦线法定义和切线法定义,给出了一元凸函数的折线法定义,讨论了凸函数的连续性等分析性质[10];证明了一元凸函数概念的一些等价形式,归纳了凸函数的连续性及可微性结论,得到了规划论中有用的极值命题[11].
随着凸函数在线性规划等领域的应用越来越广泛,学者们开始研究多元凸函数的连续性问题.如:研究了三元凸函数的连续性问题,给出了三元凸函数连续性的证明,在证明区域内一点连续时假定了该点的函数值为零[12];给出了开凸集上凸函数连续性的一个简单证法,所采用的思想与文献[12]接近[13];利用卡氏积和集合的方法证明了n维欧氏空间上的有限凸函数必是连续函数[14].
本文将研究n维欧氏空间中开凸集上n元凸函数连续性的证明:将文[12]证明三元凸函数连续性的内点表示方法用于证明n元凸函数的连续性,且无需假定连续点的函数值为零;将文[15]利用左右导数的存在性证明一元凸函数的连续性,推广为利用方向导数的存在性证明n元凸函数的连续性. 这两种方法分别称为内点表示证明法和方向导数证明法.
1 内点表示证明法

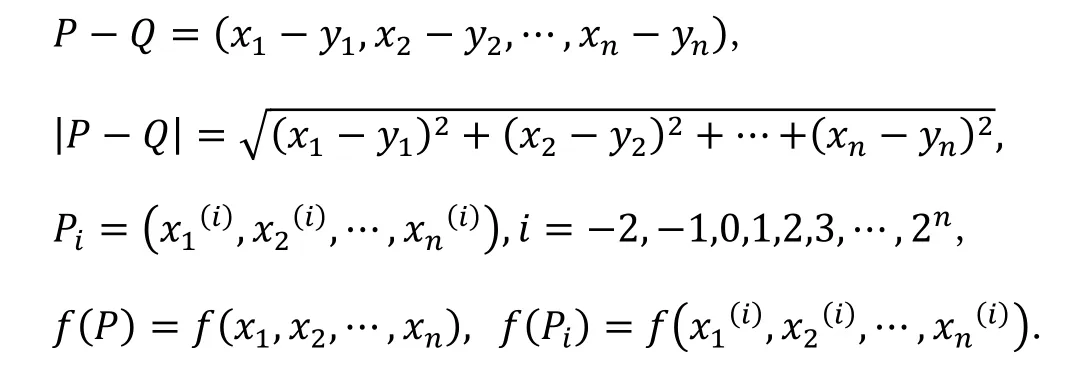
将文[12]中三元凸函数的定义推广为n元凸函数的定义.
定义1[12]设D是n维欧氏空间Rn的开凸集,f(x1,x2,…,xn)是D上的n元函数,如果对于任意两点P1,P2∈D及任意实数λ ∈[0,1],恒有

则称f(x1,x2,…,xn)是Rn中开凸集D上的下凸函数,简称凸函数.
类似于文[12]中的引理1,可将其在三维欧氏空间的结果推广到n维欧氏空间.
引理1[12]设C是n维欧氏空间ℝn中以P1,P2,…,P2n为顶点的n维长方体,则

将文[12]中三元凸函数的连续性推广为n元凸函数的连续性,并用内点表示证明法.
定理1[12]设f(x1,x2,…,xn)是n维欧氏空间Rn的开凸集D上的凸函数,则它是D上的连续函数.
证明一(内点表示证明法) 任取一点P0∈D,因D是ℝn的开凸集,所以存在以P0为中心边长为d的n维正方体C,使其完全含于D的内部.设C的2n个顶点分别为P1,P2,…,P2n,根据引理1,对于任给的P ∈C,存在λi≥0,且,使得P=.由于f(P)是凸函数,所以
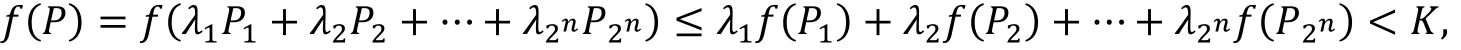
其中K =1+max1≤i≤2n{f(Pi)}. 由P0∈C ⇒f(P0)≤K-1 <K,从而有L:=K-f(P0)>0为正的常数.
下证f(P)在点P0连续,即只需要证对于任给的正数ε >0,存在点P0的一个邻域U,使得当P ∈U时,成立|f(P)-f(P0)|<ε即可.对于任给的正数ε >0,取以P0为中心边长为(dε)/L的n维正方体作为P0的邻域U.任取P ∈U,可以得到如下线性表示:


由于f(P)是开凸集D上的凸函数,所以

由此可得

即|f(P)-f(P0)|<ε,故凸函数f(x1,x2,…,xn)在开凸集D内任意一点P0连续,从而f(x1,x2,…,xn)在开凸集D上连续.
2 方向导数证明法
文[15]利用一元凸函数左右导数的存在性证明了一元凸函数的连续性,我们希望将这一证明方法应用于n维欧氏空间中开凸集上n元凸函数连续性的证明.但在推广过程中遇到了一个问题,就是由于维数的增加左右导数在高维中已不再适用.我们提出了解决这个问题的方法,用比左右导数更一般的方向导数来替代一元函数的左右导数.
引理2n元函数f(x1,x2,…,xn)在开凸集D上为凸函数的充分必要条件是:对于D内任意共线且互异的3 点P1,P2,P3,当P2位于P1与P3之间时,总有

证明(必要性) 设f(P)是开凸集D内的凸函数.根据P1,P2,P3共线互异且P2位于P1与P3之间,所以存在λ ∈(0,1),使得P2=λP1+(1-λ)P3,且
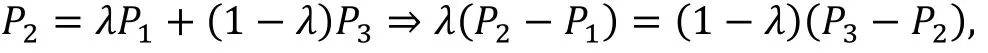
从而有

根据凸函数定义,有f(P2)=f(λP1+(1-λ)P3)≤λf(P1)+(1-λ)f(P3). 由此可得

在式(2)左右两边的式子分子分母分别乘以正数|P2-P1|和|P3-P2|, 可得

在上式中利用式(1)可得
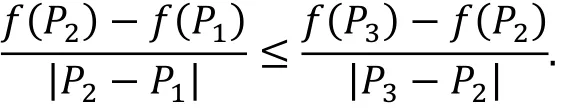
(充分性) 设P1,P2,P3共线互异且P2位于P1与P3之间,总有

任取P1,P3∈D,记P2=λP1+(1-λ)P3,λ ∈(0,1),则P1,P2,P3共线互异且P2位于P1与P3之间,因此式(3)成立.根据必要性的证明过程,由P2=λP1+(1-λ)P3可推得

则由式(3)和式(4)可式得

上式约分后,得到 λ[f(P2)-f(P1)]≤(1-λ)[f(P3)-f(P2)]. 整理后可得

将P2=λP1+(1-λ)P3代入上式可得

故n元函数f(x1,x2,…,xn)在开凸集D上为凸函数.
引理3设n元函数f(x1,x2,…,xn)是开凸集D内的凸函数.对于任给的P0∈D,过点P0作一直线l,设P0的一端为直线l的正向l+,P0的另一端为直线l的负向l-.则以下2 个极限存在
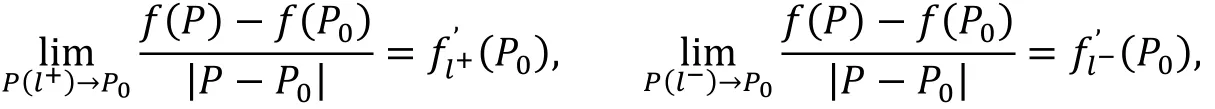
且fl-’ (P0)≥-fl+’ (P0)或fl+’ (P0)≥-fl-’ (P0).
证明设l是过点P0的一条给定的直线,P-2,P-1,P0,P1,P2在直线l上且位于开凸集D内的互不相同的5 点,P-1位于P-2与P0之间,P0位于P-1与P1之间,P1位于P0与P2之间.因此|P2-P0|=|P2-P1|+|P1-P0|. 本文规定为l的正向(记为l+),为l的负向(记为l-).由引理2 可得
由式(5)中第3 个不等式得
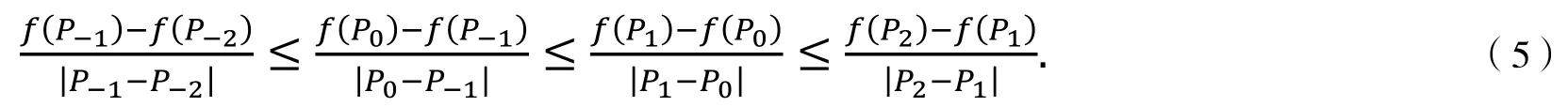

利用|P2-P0|=|P2-P1|+|P1-P0|可得

上式移项合并后可得


这说明在直线l的正向l+上,当点P沿l正向l+趋向于P0时,即当P(l+)→P0时,比值[f(P)-f(P0)]/|P-P0|单调递减,且有下界[f(P0)-f(P-1)]/|P0-P-1|,所以必有极限,记

由式(5)和式(6)可得

同乘以(-1)得

类似于前面的证明,可得

这说明在直线l的负向l-上,当点P沿l负向l-趋向于P0时,即当P(l-)→P0时,[f(P)-f(P0)]/|P-P0|单调递减,且有下界-fl+’ (P0),所以必有极限,记

且fl-’ (P0)≥-fl+’ (P0)或fl+’ (P0)≥-fl-’ (P0).
下面给出定理1 的第2 种证明方法:
定理1 的证明二(方向导数证明法) 设f(x1,x2,…,xn)是n维欧氏空间Rn的开凸集D上的凸函数,我们证明它是D上的连续函数.只需证明,对任给的P0∈D,f(x1,x2,…,xn)在点P0连续即可.即只需要证对于任给的正数ε >0,存在点P0的一个邻域U,使得当P ∈U时,成立|f(P)-f(P0)|<ε即可.
连接点P0与P得到线段,在线段上取一点P1(P1≠P0,P),记线段所在直线为l.我们规定为直线l的正向l+,为直线l的负向l-.根据引理3 及其证明过程可知
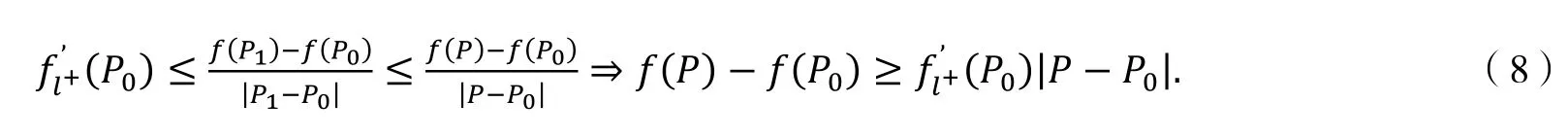
另一方面,有

从而有

联合式(8)和式(9)可得
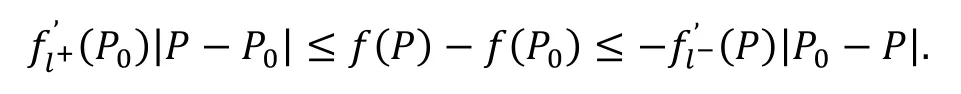
由此可得
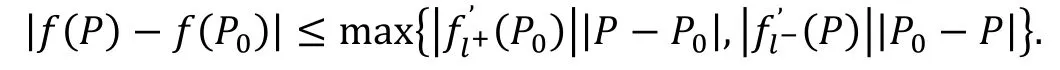

即|f(P)-f(P0)|<ε. 故n元函数f(x1,x2,…,xn)在点P0连续,从而在开凸集D上连续.

