利用光强判别法改进超声光栅测量水中声速实验

董玮涔，何旭东

(北京师范大学 物理学系,北京 100875)

超声波是频率高于20 kHz 的机械波，它在液体中传播时会造成液体的密度分布不均匀(呈周期性变化). 当光通过时会产生类似于通过透射光栅的衍射现象. 故将超声导致的液体中的“光栅”称作“超声光栅”.

利用超声光栅测量声速，可对液体的一些性质进行研究,如，探究声速与溶液浓度、声速与溶液温度的关系[1]，液体体积弹性模量与浓度的关系[2]，等等. 因此,利用超声光栅高精度地测量声速就显得尤为重要，文献[3-4]探寻超声腔的结构以减少损耗，拓展测量液体范围，提高精度. 本文设计了利用分光计实现高精度测量液体声速的方法.

1 实验原理

1.1 驻波的形成

假设超声纵波在液体中声强衰减为

If=Ie-ld,

(1)

其中d为声波传播距离，l为与液体有关的衰减系数，在d较小时 (在实验中，水槽长度D=30.00 mm)，可以认为e-ld≈1，所以大致认为在传播过程中，波的振幅没有发生改变，只在反射瞬间有振幅的衰减，振幅乘以e-lD. 再考虑在声波反射面上的声强衰减,其反射系数为

(2)

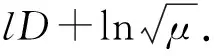
设压电陶瓷发出的初始波为

y=A0cos (ωt-kx),

(3)

设水槽长度为

D=(N+a)Λ,a∈[0,1),N∈Z+.

(4)

其中，Λ为超声波在水中的波长. 考虑无穷多次的反射波的叠加，以及半波损失，计算结果为

yf=A0Asin (kx)cos (ωt-b),

(5)

当ld一定时，b是常数，则

(6)

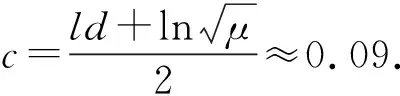
1.2 光栅衍射

式 (5) 示意图如图1(a) 所示，yf大于0的部分，液体沿正方向移动；yf小于0的部分，液体沿负方向移动.B,D,F处水的密度最大，C,E处水的密度最小. 水密度周期即yf的周期.

本实验中，由式(4)可推知水密度周期为Λ，即超声波在水中的波长.

超声驻波场引起的介质折射率分布可以写成

n(x)=n0+Δncos (kx),

(7)

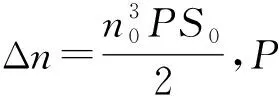
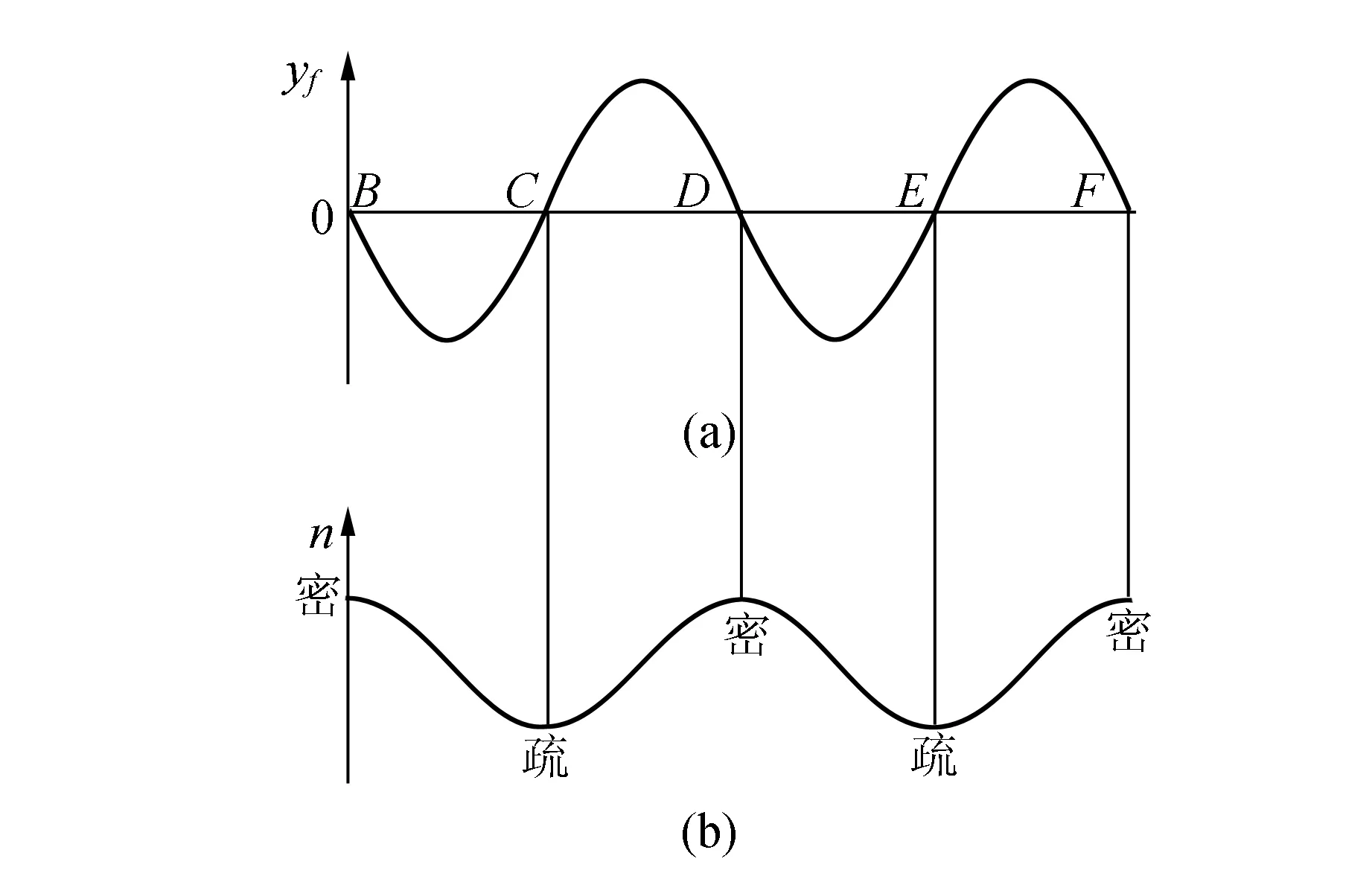
图1 超声光栅衍射原理示意图

在光束近似垂直入射情况下，液体超声光栅实验中的声光相互作用为典型的Naman-Nath衍射[5]. 光栅方程为[6]

dsinθ=jλ,

(8)

其中，光栅常量d=Λ,j为条纹级数，λ为光波长.

测量衍射光对应的衍射角θ即可求出超声波波长，据此求出声速.

2 传统分光计测角法

实验装置示意图如图2所示. 使用信号发生器控制超声水槽中的压电陶瓷调节超声频率，让平行光束垂直超声波传播方向通过水槽，用分光计进行观察与测量. 若超声形成驻波，则可观察到清晰的衍射条纹.

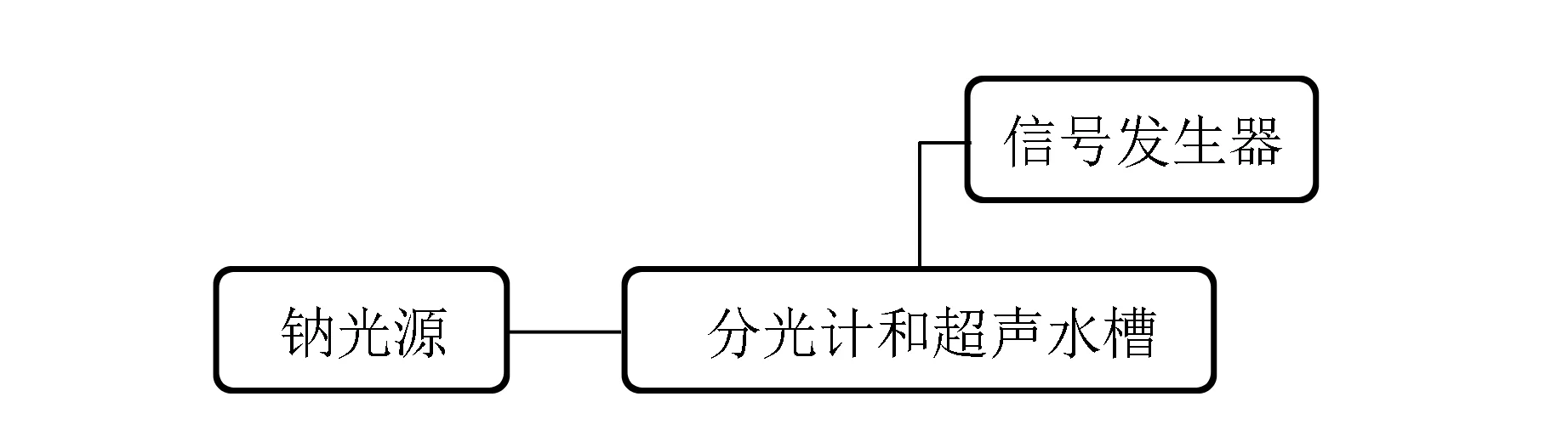
图2 分光计测角法实验装置示意图

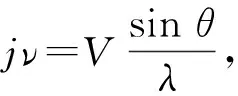
其中V=Λν，即水中的声速，ν是超声波的频率. 实验中，为了提高精度，测量零级条纹左右2条同级条纹. 鉴于分光计有左右2个游标，将2条纹的左游标读数相减除以 2 即为该衍射级次的衍射角，右游标同理. 原始数据如表1所示. 另外，实验用钠光灯，钠光波长λ=589.3 nm，代入公式进行计算.

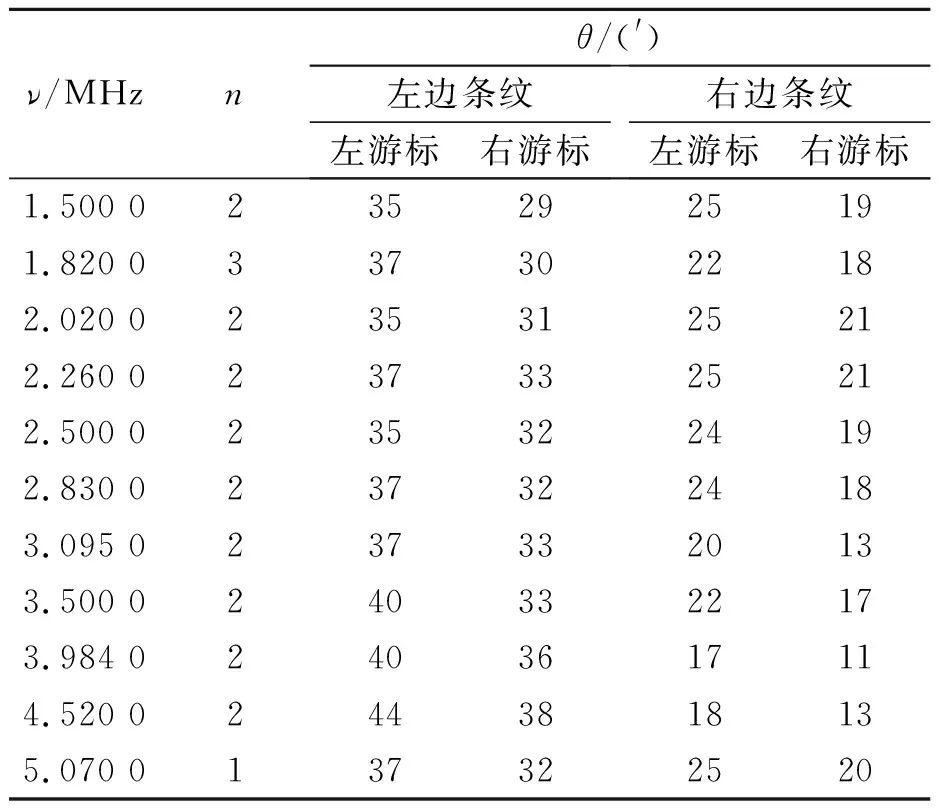
表1 分光计测角法原始数据

使用Matlab线性拟合,如图3所示,得其斜率即为超声波水中速度

V=1 492(1 386, 1 597) m/s,

式中括号内数据为Matlab给出的置信区间.

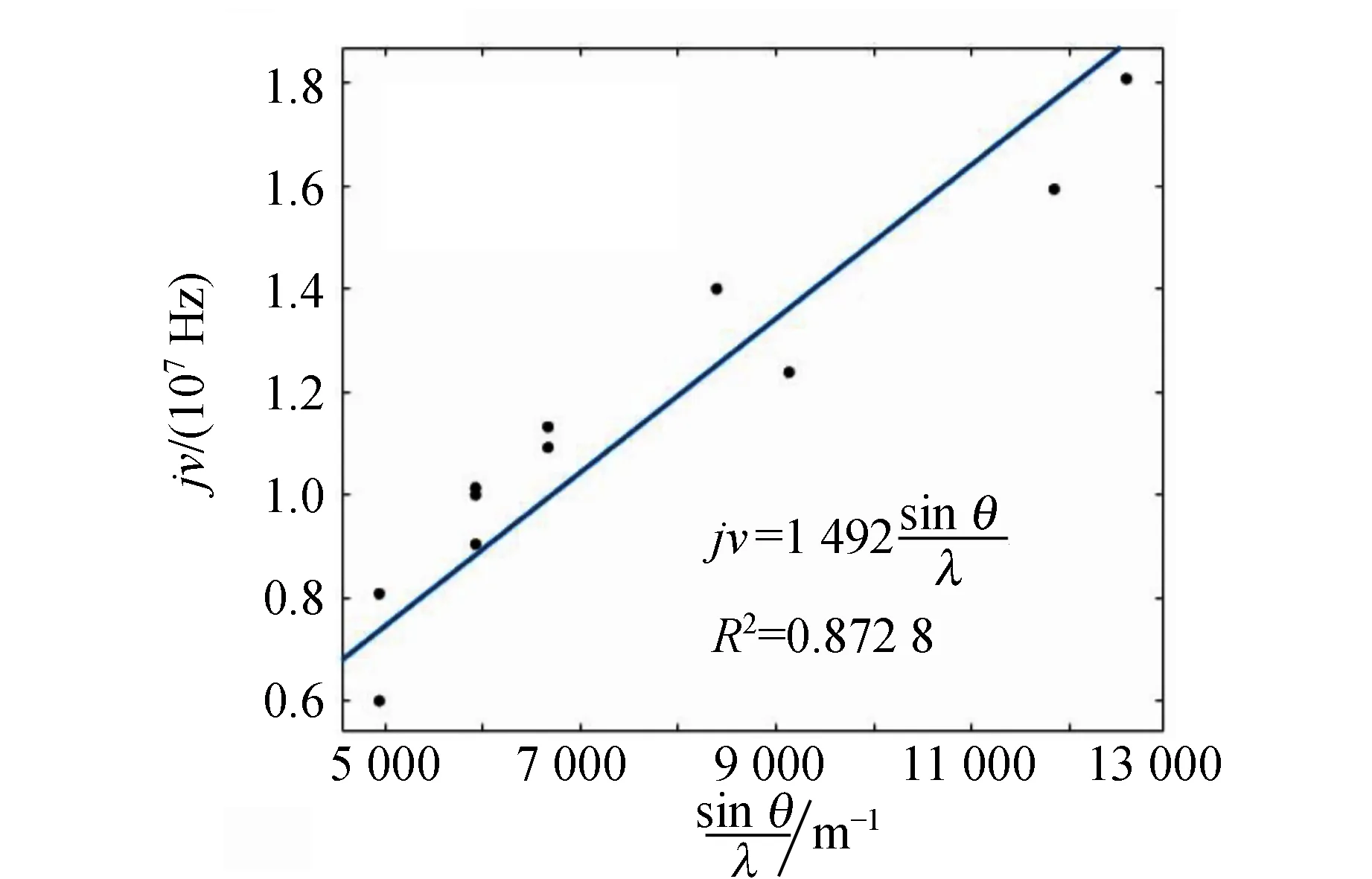
图的关系

分别计算出不同频率的超声波对应测量出的声速，最后得出声速极值分别为

Vmax=1 711.9 m/s,Vmin=1 215.5 m/s.

两者相差较大，且斜率置信区间较大，因此试图寻求新的测量方法来得到声速.

3 传统实验的改进

3.1 光强判别法

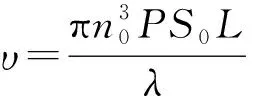
图 的计算曲线[5]

根据式(6), 用Matlab绘图可得A与a的关系见图5. 分析得a为0和1/2时，即pΛ=2D(p∈Z+)时，光强最大.

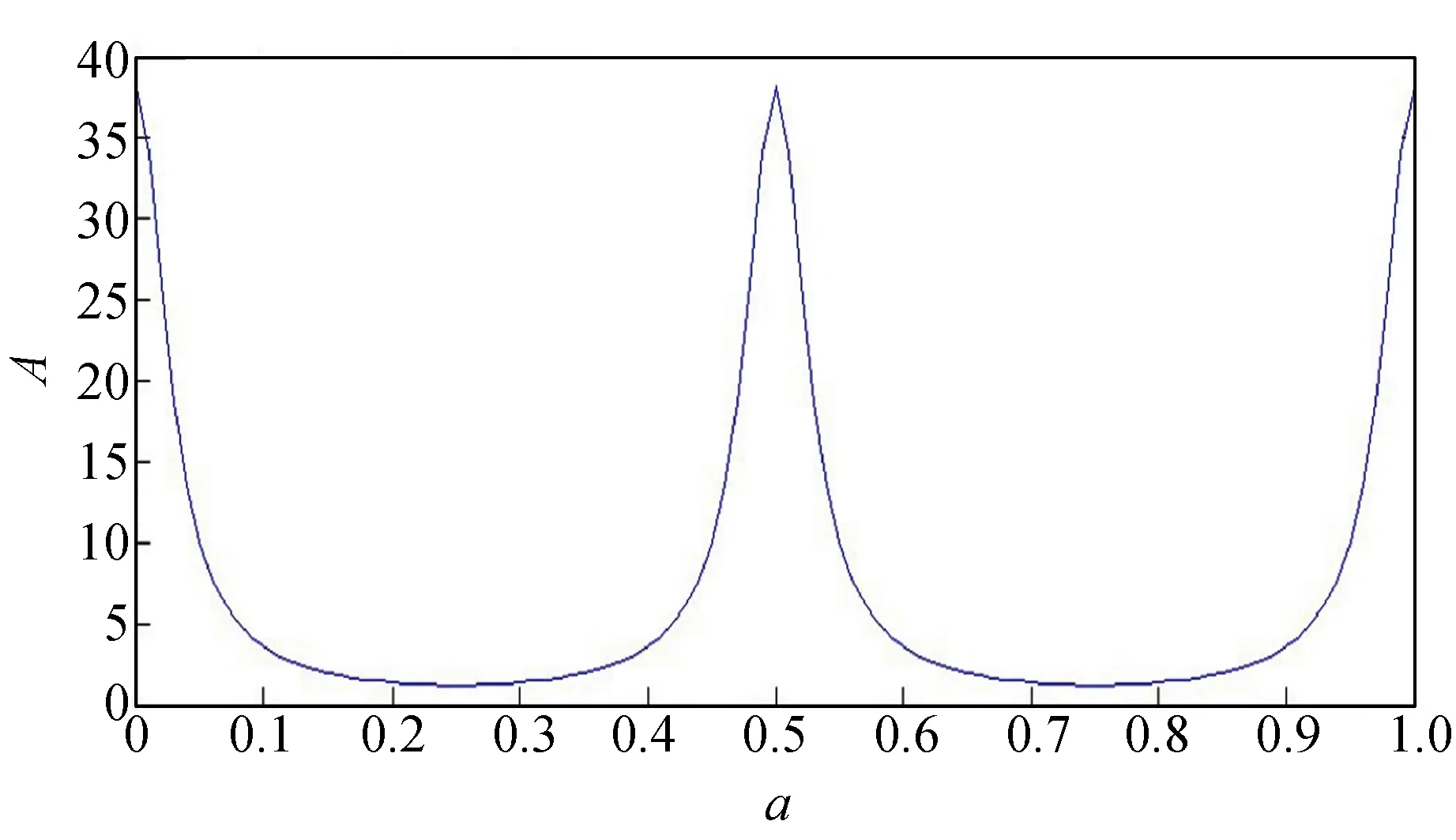
图5 A与a的关系

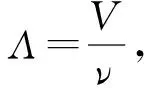
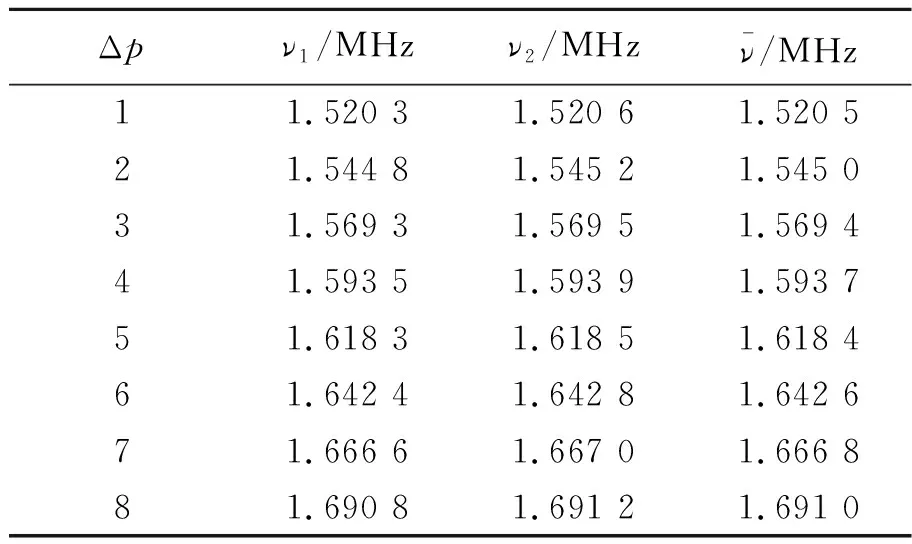
表2 光强判别法原始数据

使用Matlab线性拟合，如图6所示，得其斜率即为超声波在水中的速度.

V=1 462(1 458,1 466) m/s,

对比分光计测角法的结果，可知光强判别法更加精准.

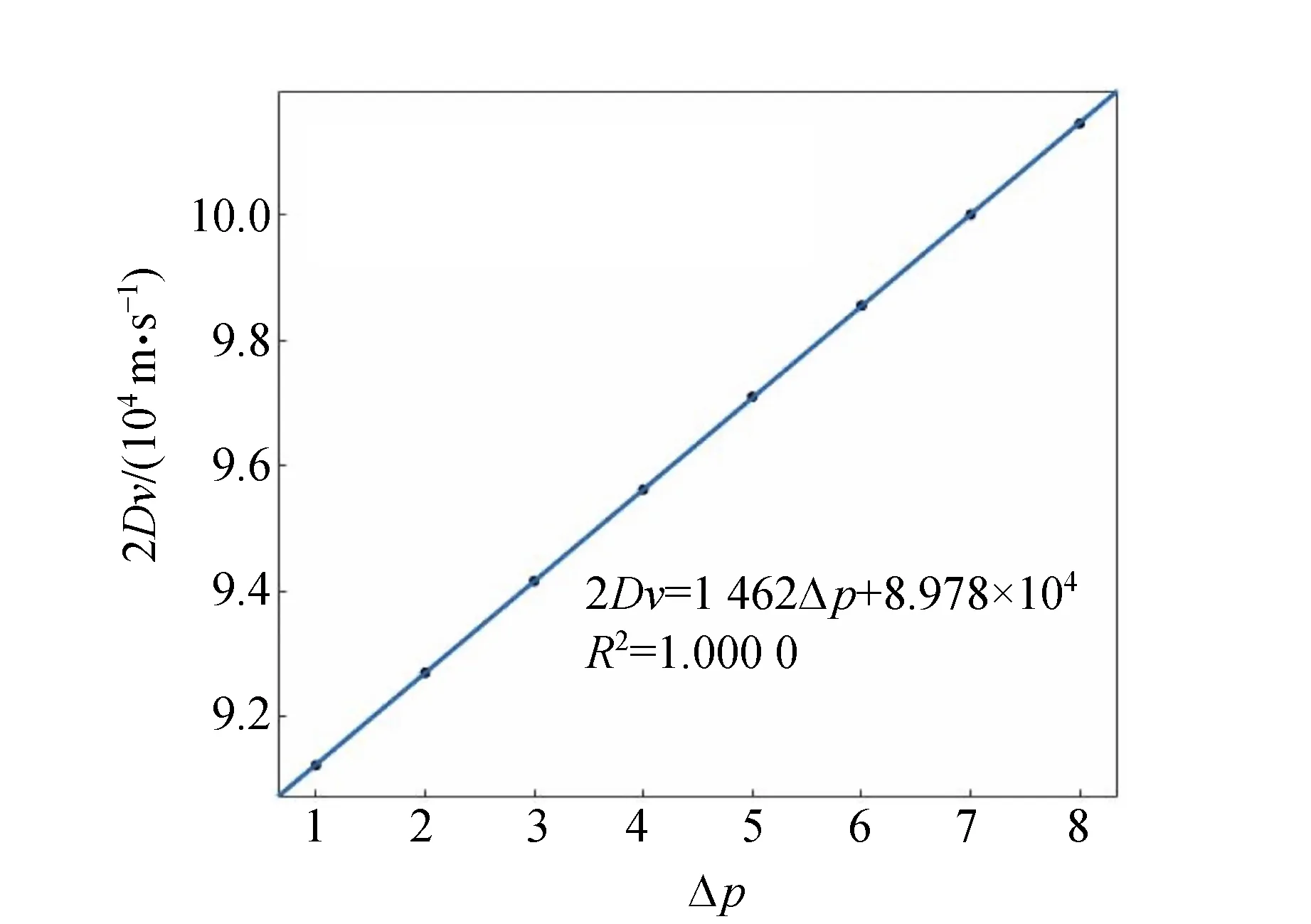
图6 2Dν-Δp的关系

注意：图6中p的定义见式 (4)，具体实验中无法得知p的具体数值. 但由于只需求斜率，只需关注p的相对变化Δp，此处令增大超声频率时记录的第1个光强极大处Δp为1，下文同理.

3.2 改进光强判别法

由于肉眼观察不够精准，改进了光强判别法(图7)，使用摄像头实时记录衍射图像，并编写LabVIEW程序(图8)来采集数据，LabVIEW运行时截图见图9，其中:摄像头实时记录衍射图像；用LabVIEW来读出光强，控制等时等步长扫频分析条纹光强；去掉0级条纹数据，将其他级衍射条纹光强相加，做其与频率的曲线.

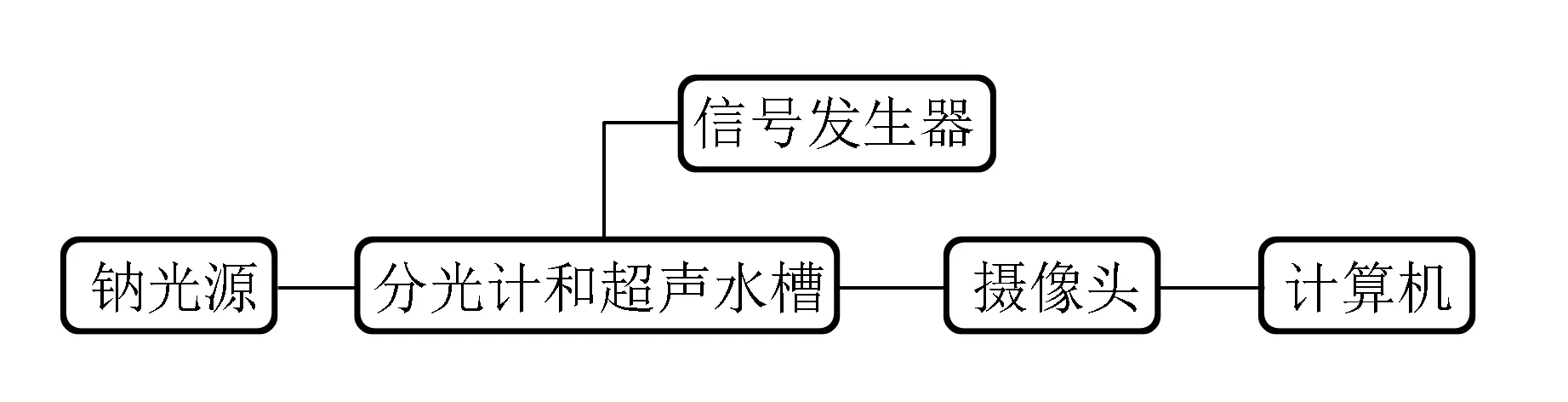
图7 改进光强判别法实验装置示意图

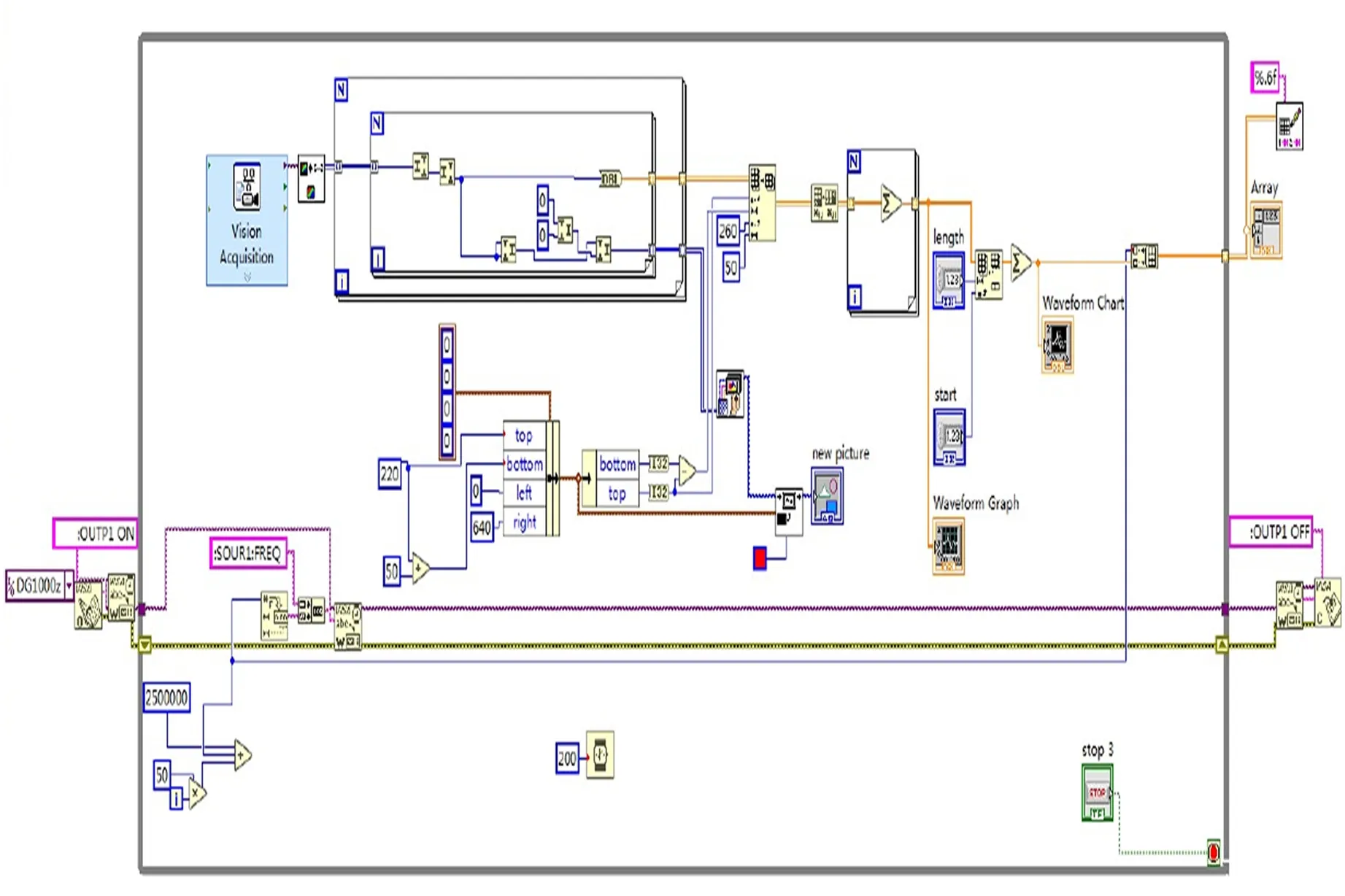
图8 LabVIEW程序框图

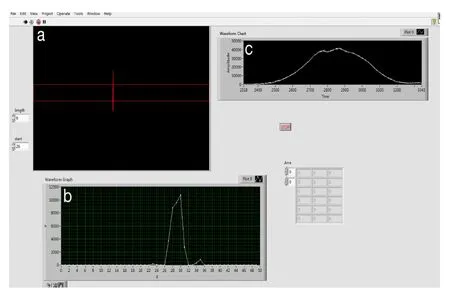
图9 LabVIEW运行时截图

导出数据做图10, 由于光强最大处并不足够光滑，采用的处理方法为：选择图10中的一段对于每个峰求得光强为104时对应的2个频率，取其平均值得到光强最大所对应的频率. 原始数据见表3. 处理后做图11，使用Matlab线性拟合得其斜率即为超声波水中速度

V=1 460(1 459, 1 462) m/s,R2=1.0000 .

可以看出改进之后置信区间更小，更精确.

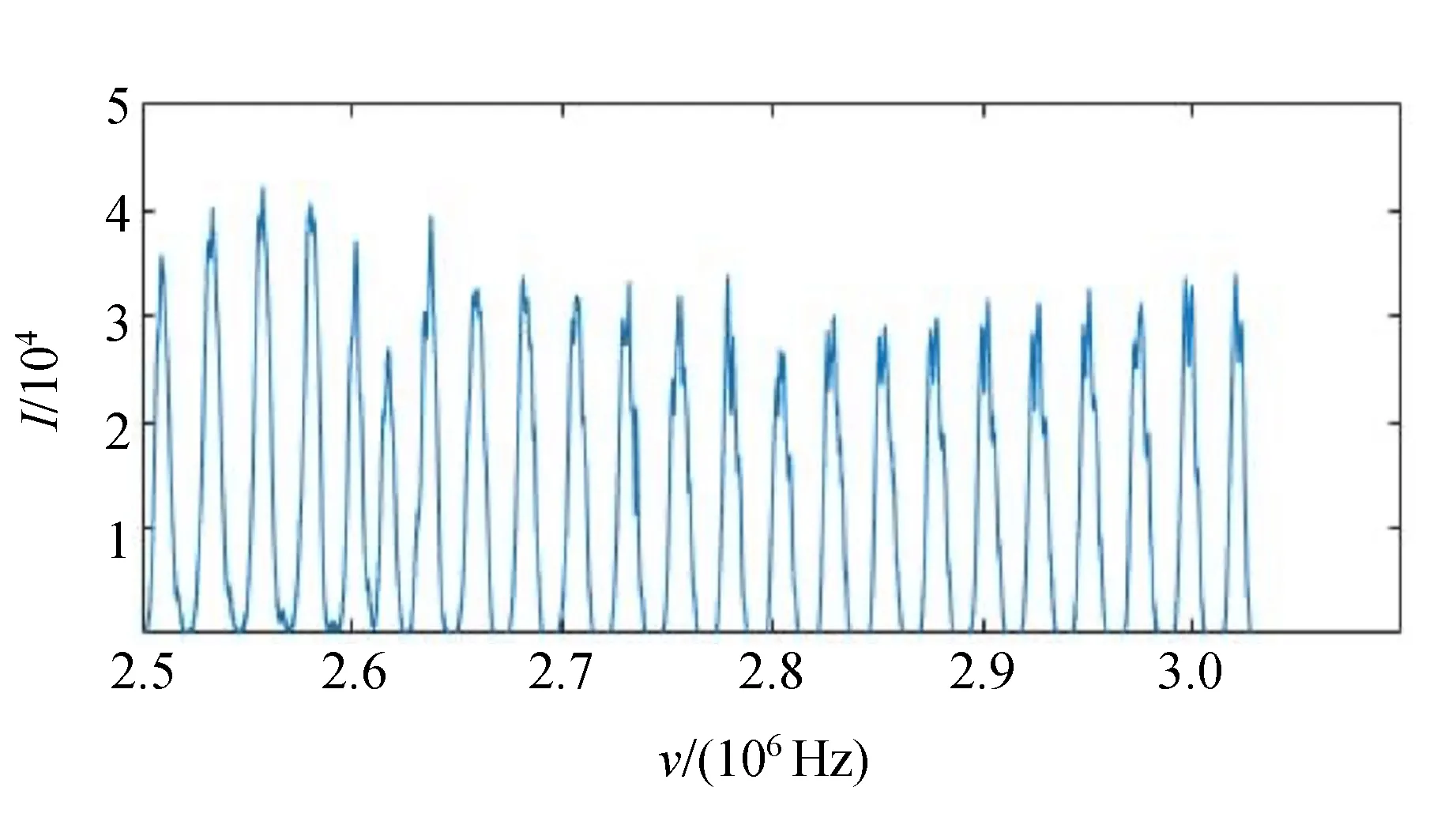
图10 频率与光强的关系

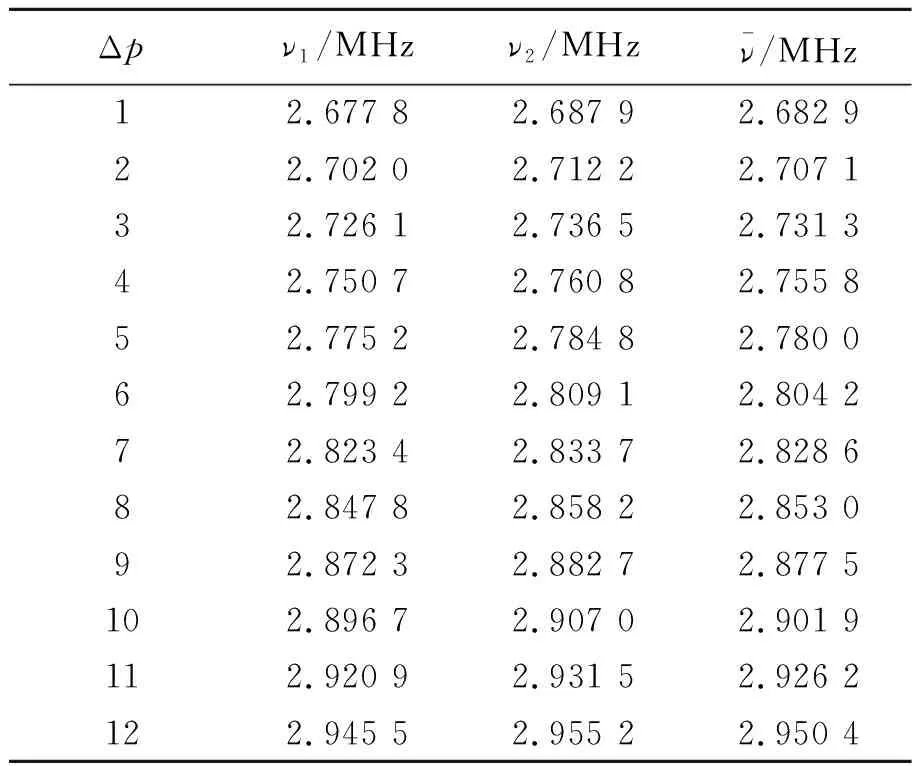
表3 改进光强判别法原始数据

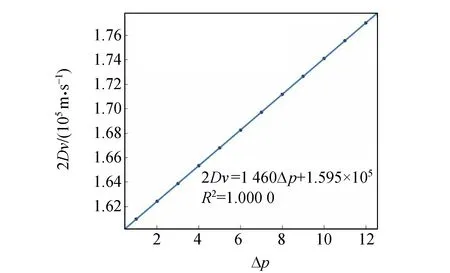
图11 改进后2Dν-Δp的关系

4 结束语

在分光计测角度时，超声频率较小时衍射光强较大但是衍射角较小，但超声频率过高时衍射光强较小不便读数. 光强判别法避免了这一问题，在频率较低时也能非常准确地测量到光强随频率的连续变化，可以精确地得出超声在水中的声速. 并且采用计算机处理数据，减少了误差.

致谢：感谢北京师范大学物理学系的白在桥副教授、李晓文副教授对本实验提供的帮助.