RLC谐振与物理共振的原理共性

李潮锐

(中山大学 a.物理学院；b.物理国家级实验教学示范中心，广东 广州 510275)

核磁共振是量子现象，但通常本科量子力学课程未能对核磁共振吸收频域展宽和时域弛豫给出严谨的理论描述，从而也增加了核磁共振实验的教学难度. 由经典振动动力学可知，共振展宽和弛豫等现象源于阻尼力(矩)的作用. 基于角动量定理并引入阻尼力矩的核磁共振半经典理论，可以得到与经典共振相似的动力学行为的布洛赫方程组. 另一方面，由于RLC电路稳态和暂态过程与经典受迫、共振和阻尼振动等现象的频域和时域特性相似[1],可以认为RLC谐振、经典共振和核磁共振(布洛赫方程组)三者具有明显的物理原理共性. 关注上述逻辑关系，既有助于深刻理解核磁共振的物理原理，又使核磁共振实验事实更加浅显易懂. 相对于经典振动实验观测，RLC电路谐振特性测量方法更简单，且易于调节实验条件而直观地展示共振展宽和弛豫等实验事实. 文献[2-4]已介绍RLC电路相位测量及其阻抗或导纳分析方法，本文重点分析RLC电路中各元件(或组合)的作用及其与共振物理参量之间的对应关系. 根据基尔霍夫电压定律和电流定律分别建立RLC串联电路和并联电路的二阶微分方程， 分析表明RLC串联电路中电容C两端的电压和RLC并联电路中电感L两端的电压分别类似于经典振动的振动位移和振动速度，利用频域和时域实验事实展示RLC电路与经典振动的物理共性. 由布洛赫方程组得到核磁共振半经典动力学描述，结合核磁共振实验事实，凸显RLC谐振、经典共振和核磁共振的原理共性.

1 实验技术方法

RLC串联电路如图1所示，电感L、电容C、(波段开关)步进式电位器RS和电压源(经隔离变压器)组成串联回路. 回路串联电阻R由电位器RS和电感L的内部损耗电阻RL串联而成的等效电阻.

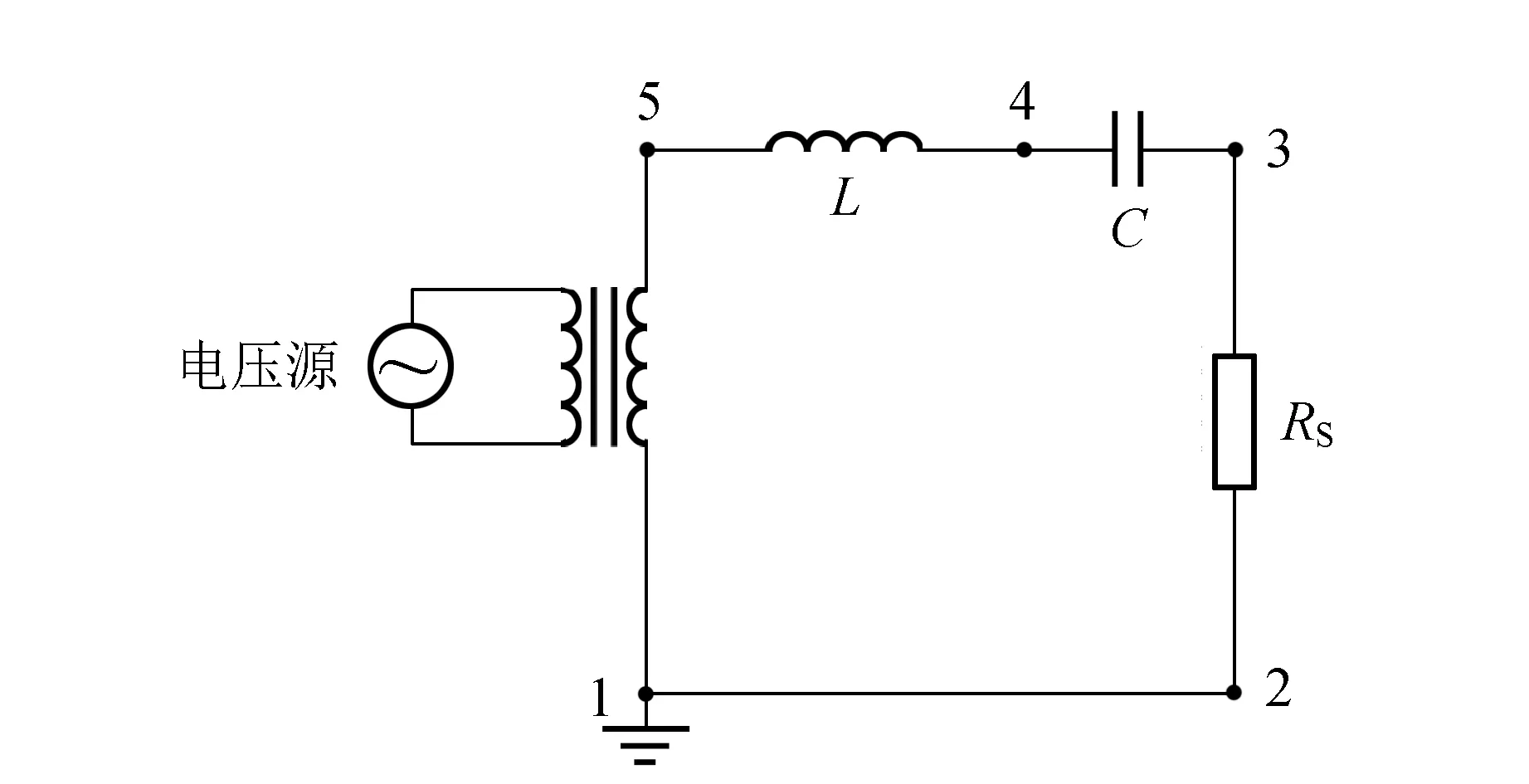
图1 RLC串联实验接线图

观测响应量uC及duC/dt稳态频域特性时，使用泰克示波器MDO4034观测1～5间电压uE、3～4间电压uC(使用差分探头)和2～3间电压uS. MDO4034内置波形发生器提供频率可调的简谐源信号.

观测响应量uC及duC/dt暂态时域过程时，信号采样方法同上. MDO4034内置波形发生器输出合适固定频率的方波源信号.

RLC并联电路如图2所示，电感L、电容C和(波段开关)步进式电位器RP先并联，再与取样电阻RS和电压源(经隔离变压器)组成回路.RLC并联回路等效电阻R由电位器RP和电感L的内部损耗电阻RL并联而成.

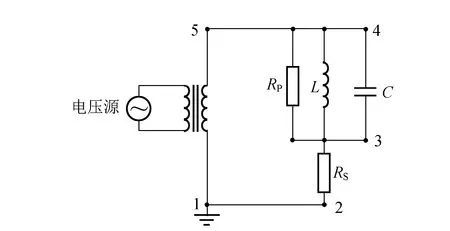
图2 RLC并联实验接线图

观测响应量变化率diL/dt稳态频域过程时，使用泰克示波器MDO4034观测1～5间电压uE、3～4间电压uC(使用差分探头)和2～3间电压uS.RLC并联回路驱动电流iE由取样电阻RS两端压降uS求得. MDO4034内置波形发生器提供频率可调的简谐源信号.

实验元件参量：C=13.25 nF，L=19.63 mH，损耗电阻RL=82.39 Ω. 图1中RS步进阻值39 Ω；图2中RP步进阻值39 kΩ，取样电阻RS=99.16 Ω.

采用文献[5]方法测量核磁共振稳态吸收，使用苏州纽迈核磁共振成像分析仪NMI120-015V-I观测横向弛豫. 实验样品为CuSO4饱和水溶液.

2 实验结果及分析

2.1 RLC串联谐振特性

根据基尔霍夫电压定律，图1RLC串联回路电压满足

uL+uR+uC=uE

,

(1)

其中，uL，uR和uC分别为电感L、电阻R和电容C两端电压(压降)，uE为信号源经隔离变压器输出电压. 若回路电流为i，则

(2)

(3)

(4)

考虑信号源输出电压为uE=u0cos (ωt)情形，将式(3)和(4)代入式(1)，可得

(5)

若以u0cos (ωt)为激励而uC为响应量，式(5)与弹簧振子的动力学方程[6]比较可知，式(5)左侧分别为惯性项、阻尼项和弹性项，右侧为激励项(或策动项). 式(5)可改写为

(6)

uC=A0(ω)cos (ωt+φ)+B0(ω1)e-β tcos (ω1t+φ1),

(7)

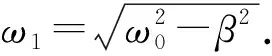
2.1.1RLC串联稳态频域

由上述分析可知，RLC串联电路由式(6)描述电容C两端电压uC对电压源信号u0cos (ωt)激励作用的响应. 实验事实也显示稳态过程uC与激励源信号u0cos (ωt)存在相位差φ，而且响应量uC稳态过程幅值A0(ω)和相位φ都随激励频率而改变.

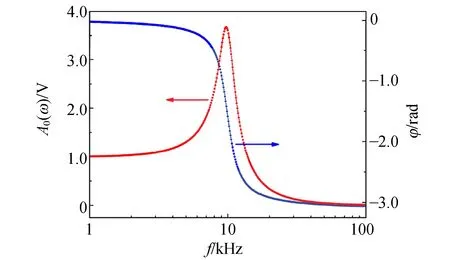
图3 RLC串联响应量幅值及其相位频率特性

由式(3)可知，若测量RLC串联电路中电阻R两端电压uR获得回路电流i，则可得响应量uC变化率duC/dt的实验值. 由于电阻R包含了电感损耗电阻RL而无法直接测量电压uR，实验改由测量电位器RS两端的电压uS获得回路电流i.

考虑RLC串联回路的电流i关系

(8)

可得

(9)

由式(9)可知，通过测量RS两端电压uS可得到响应量uC变化率duC/dt的实验数据.

图4显示与图3相同实验参量的稳态过程响应量变化率duC/dt的幅值和相位随频率变化情况. 与图3比较可知，图4所示响应量变化率duC/dt的相位比响应量uC的相位超前π/2. 由实验结果可见，RLC串联电路稳态过程响应量变化率duC/dt与弹簧振子的振动速度的物理过程相似.

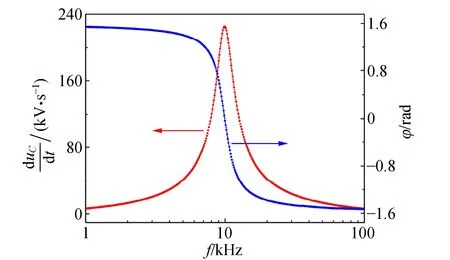
图4 RLC串联响应量变化率幅值及其相位频率特性

2.1.2RLC串联暂态时域

考虑电压源输出信号为低频方波，即uE交替输出2个不同电平信号，使电容C两端电压uC都经历了暂态过程才到达稳定状态，或称弛豫过程. 在弱阻尼情形，RLC串联响应量uC及其变化率duC/dt暂态时域过程如图5所示. 图5结果实验条件：方波幅值Vpp=5.00 V，频率f=500 Hz，步进式电位器阻值为38.50 Ω.

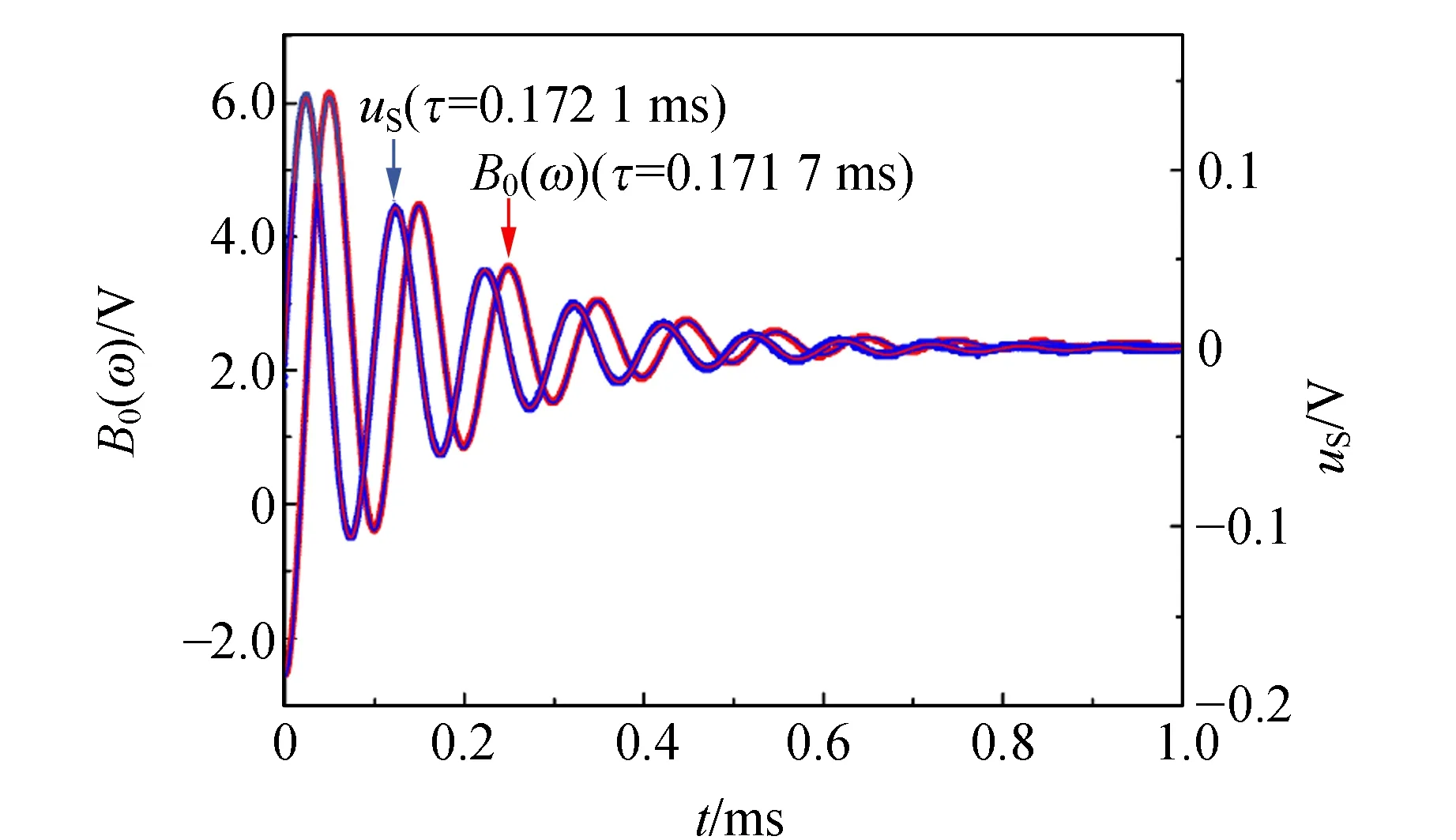
图5 RLC串联电路响应量及其变化率暂态过程

响应量uC暂态过程由式(7)右侧第2项描述,

uC=B0(ω1)e-t/τcos (ω1t+φ1),

(10)

其中，τ=1/β为衰减时间或弛豫时间. 由式(10)可知，响应量变化率duC/dt暂态时域具有与响应量uC相似的衰减过程，而且由图5的结果得到了验证.

上述理论分析和实验事实表明，RLC串联电路响应量uC等效于弹簧振子的振动位移，而uR或uS则包含着响应量变化率duC/dt信息，即类比于弹簧振子的振动速度. 不管是图3与图4稳态过程，还是图5暂态过程，实验结果都显示响应量uC与变化率duC/dt相位差π/2. 根据式(9)由uS获得duC/dt，且采用差分探头解决信号共地问题，从而实现uC和duC/dt两者同步测量. 图6为RLC串联电路谐振相图. 可见，其结果与经典振动相图[7]一致.

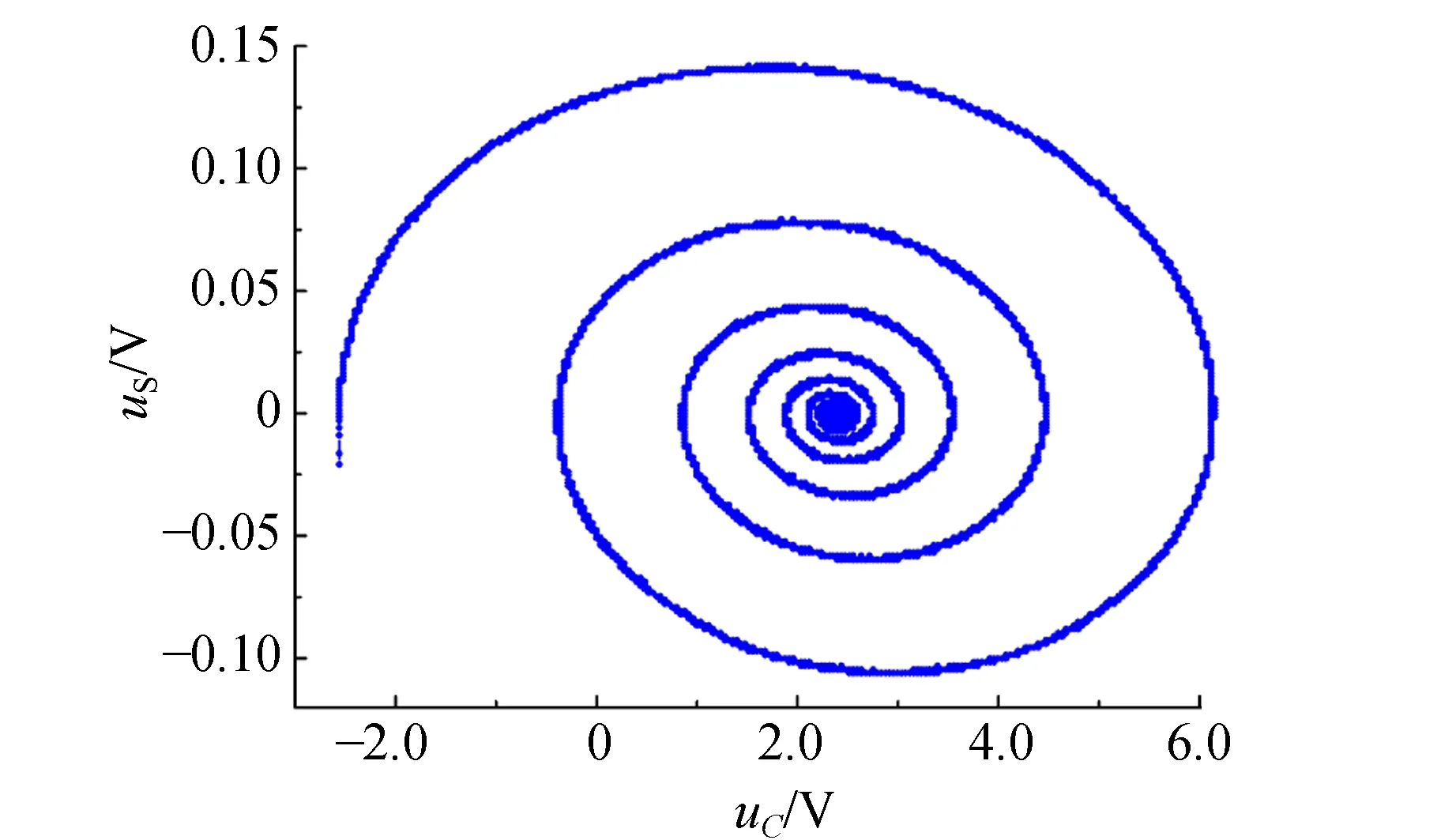
图6 RLC串联电路暂态过程相图

2.2 RLC并联谐振特性

根据基尔霍夫电流定律，图2节点3或4处的电流满足

iL+iR+iC=iE,

(11)

其中，iL,iR和iC分别为流经电感L、电阻R和电容C的电流，而iE则为信号源经隔离变压器输出的电流. 若RLC并联电路两端电压为u，那么

(12)

(13)

(14)

考虑驱动电流为iE=i0cos (ωt)情形，将式(13)和(14)代入式(11)，可得

(15)

若以i0cos (ωt)为激励而iL为响应量，同理可知，式(15)左侧分别为惯性项、阻尼项和弹性项，右侧为激励项(或策动项). 式(15)可改写为

(16)

iL=C0(ω)cos (ωt+φ)+D0(ω1)e-β tcos (ω1t+φ1),

(17)

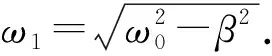
在RLC串联电路，由式(6)分析电容C两端电压uC对电压源信号u0cos (ωt)激励作用的响应. 对RLC并联电路，在电流源信号i0cos (ωt)激励作用下，以流经(纯)电感L电流iL为响应量的谐振特性则用式(16)描述. 由图2电路可知，实验上难以直接测量响应量iL，但是可以通过测量RLC并联电路两端电压u再由式(12)求得响应量变化率diL/dt. 上述分析可见：RLC并联电路以电流激励，而非串联电路所用的电压激励；RLC并联电路以响应量变化率为直接测量物理量，而串联电路则响应量及其变化率都可以直接测量.

图7显示了响应量变化率diL/dt幅值及其相位随驱动(策动)频率ω变化情况. 图7结果的实验条件：i0≈10.00 mA(uS=1.00 V，归一化)，并联RP=39 kΩ. 与RLC串联电路所得的图3和图4实验结果比较，可见RLC并联电路稳态过程响应量变化率diL/dt与经典振动速度的物理过程相似.

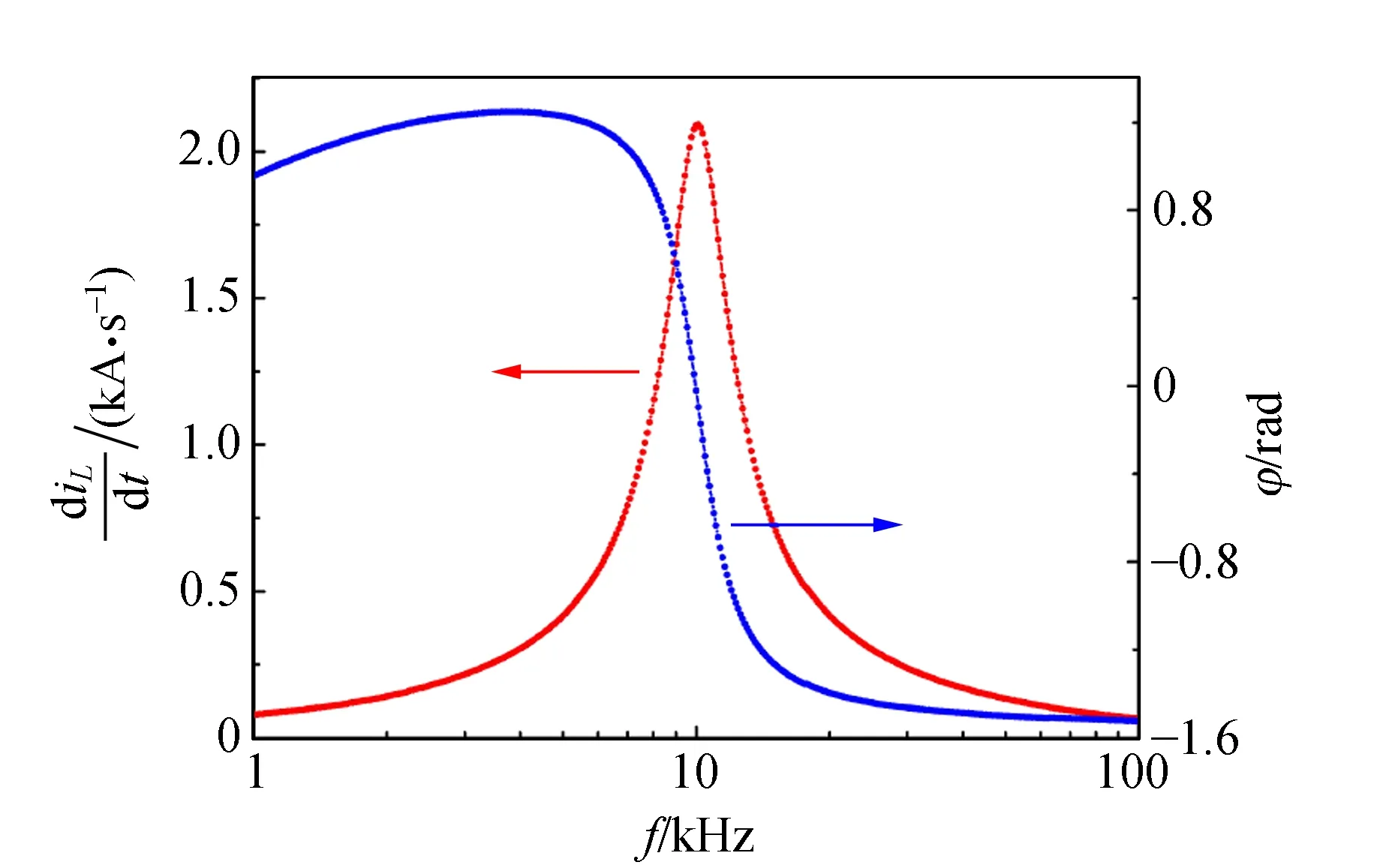
图7 RLC并联响应量变化率幅值和相位频率特性

2.3 暂态弛豫与稳态展宽

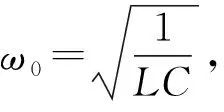
由步进式电位器调节RS,从而改变回路电阻R，根据式(6)即可改变回路阻尼系数β. 图8和图9分别为不同阻尼(即不同的回路电阻R)条件下RLC串联电路响应量uC和变化率duC/dt幅值频率特性. 实验结果表明，随阻尼增强(即随RS增大)，稳态过程响应量uC及其变化率duC/dt频域半高全宽Δf逐渐增大，同时谐振频率ω1向低频端移.

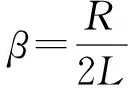
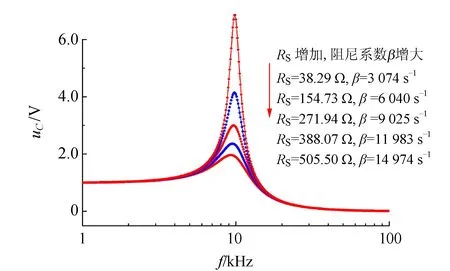
图8 不同阻尼情形RLC串联uC幅值频率特性

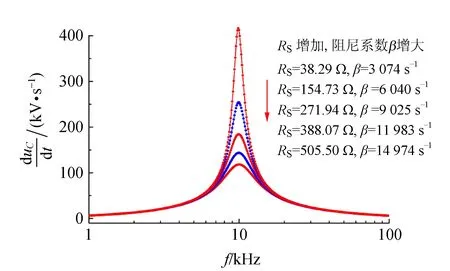
图9 不同阻尼情形RLC串联duC/dt幅值频率特性

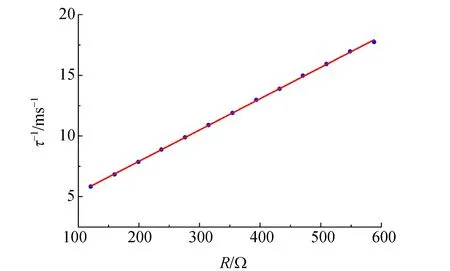
图10 RLC串联回路暂态弛豫时间τ与电阻R的关系

图8～10结果表明，随阻尼变化，当稳态过程频域半高全宽Δf增大则其对应的暂态时域弛豫时间τ缩短. 上述实验结果与经典振动理论[6]描述一致.

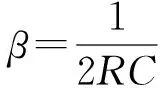
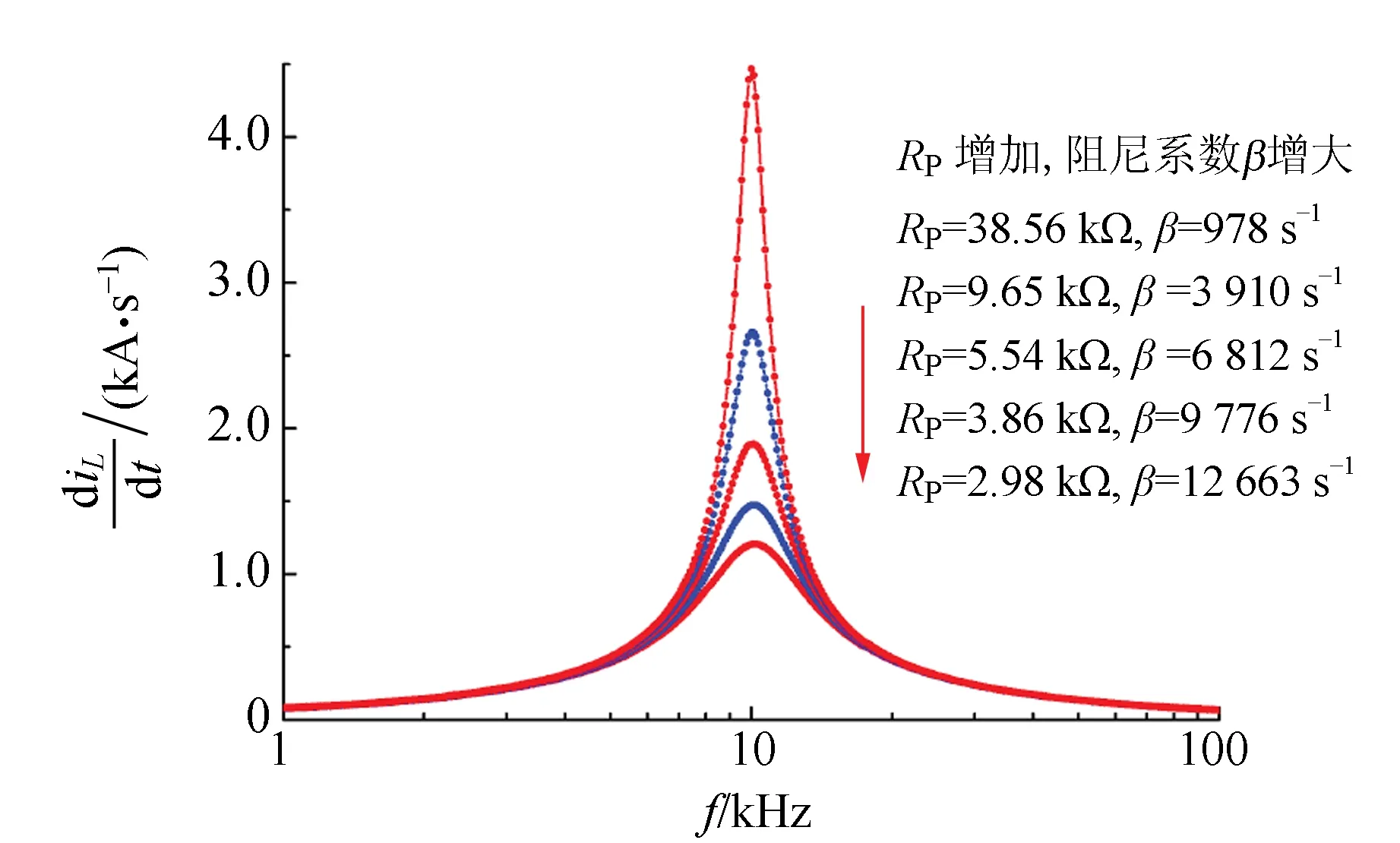
图11 不同阻尼情形RLC并联diL/dt幅值频率特性

2.4 核磁共振半经典理论

根据角动量定理并引入阻尼力矩，描述核磁共振半经典理论的布洛赫方程为

(18)

其中，B,M,TD和γ分别为外磁场、单位体积磁矩、阻尼力矩和磁旋比.

考虑外磁场

B=[b0cos (ωt)]i-[b0sin (ωt)]j+B0k，

其中，[b0cos (ωt)]i-[b0sin (ωt)]j为圆偏振射频磁场(激发光子)，且b0≪B0,式(18)可改写为布洛赫方程组

(19)

(20)

(21)

式中，T1和T2分别为纵向弛豫时间和横向弛豫时间，前者描述受激核磁矩处于激发态的寿命，后者还考虑了自旋-自旋作用所引起的退相干. 显然，T2(远)小于T1. 为了简化数学处理，分析Mx和My随时间变化时，可近似认为Mz不变. 同时，忽略B0不均匀性.

利用拉莫频率ω0=γB0，且令η=γMzb0,分别对式(19)和式(20)再次微分，可得

(22)

(23)

首先，将式(19)和式(20)分别代入式(22)和式(23)右侧，可得到

(24)

(25)

再利用式(19)中My与Mx和dMx/dt关系，及式(20)中Mx与My和dMy/dt关系，式(24)和式(25)可改写为

(26)

(27)

式中，

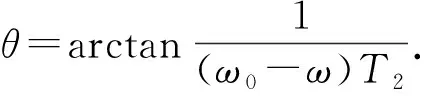
令复数Mxy=Mx+iMy，则式(26)和式(27)可合并为

(28)

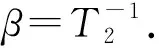
即为拉莫频率，它与阻尼系数无关. 另一差别是，简单经典振动或者RLC谐振使用线偏振驱动，而核磁共振采用圆偏振驱动. 在核磁共振过程，原子核磁矩和激发光子为整体必须同时满足能量守恒和角动量守恒，圆偏振驱动是角动量守恒所要求的. 实验上直接提供圆偏振激发光子是困难的，通常使用线偏振射频场驱动. 根据线偏振可以分解为互反方向同频圆偏振原理，其中之一可以产生有效核磁共振，另一个圆偏振光子则不起作用(质子核自旋能级中不存在可被激发的其他激发态).

考虑弱阻尼情形，方程(26)和(27)的解为

Mx=ξx(ω)cos (ωt+φ)+ζx(ω0)e-t/T2cos (ω0t+φ0),

(29)

My=ξy(ω)sin (ωt+φ)+ζy(ω0)e-t/T2sin (ω0t+φ0),

(30)

上述等式中，右侧两项分别代表核磁共振响应量Mx和My所描述的稳态和暂态(横向弛豫)过程. 其中，ξx(ω)和ξy(ω)与φ分别为稳态信号幅值及相对于激励(激发)的相位差，而ζx(ω0)和ζy(ω0)与φ0则分别为暂态信号幅值与初相位.

事实上，式(29)和式(30)描述同一物理过程在xy平面的投影，令系数ξx(ω)=ξy(ω)=ξ(ω)以及ζx(ω0)=ζy(ω0)=ζ(ω0)，式(29)和(30)可以简化为

Mx=ξ(ω)cos (ωt+φ)+ζ(ω0)e-t/T2cos (ω0t+φ0),

(31)

My=ξ(ω)sin (ωt+φ)+ζ(ω0)e-t/T2sin (ω0t+φ0).

(32)

在上述分析中，考虑了T2(远)小于T1，并假设在Mx和My变化过程中Mz近似不变. 尽管图12实验结果来自纵向弛豫和横向弛豫的共同贡献，但是不同浓度CuSO4水溶液的共振展宽与弛豫关系与RLC谐振或经典振动规律是一致的.

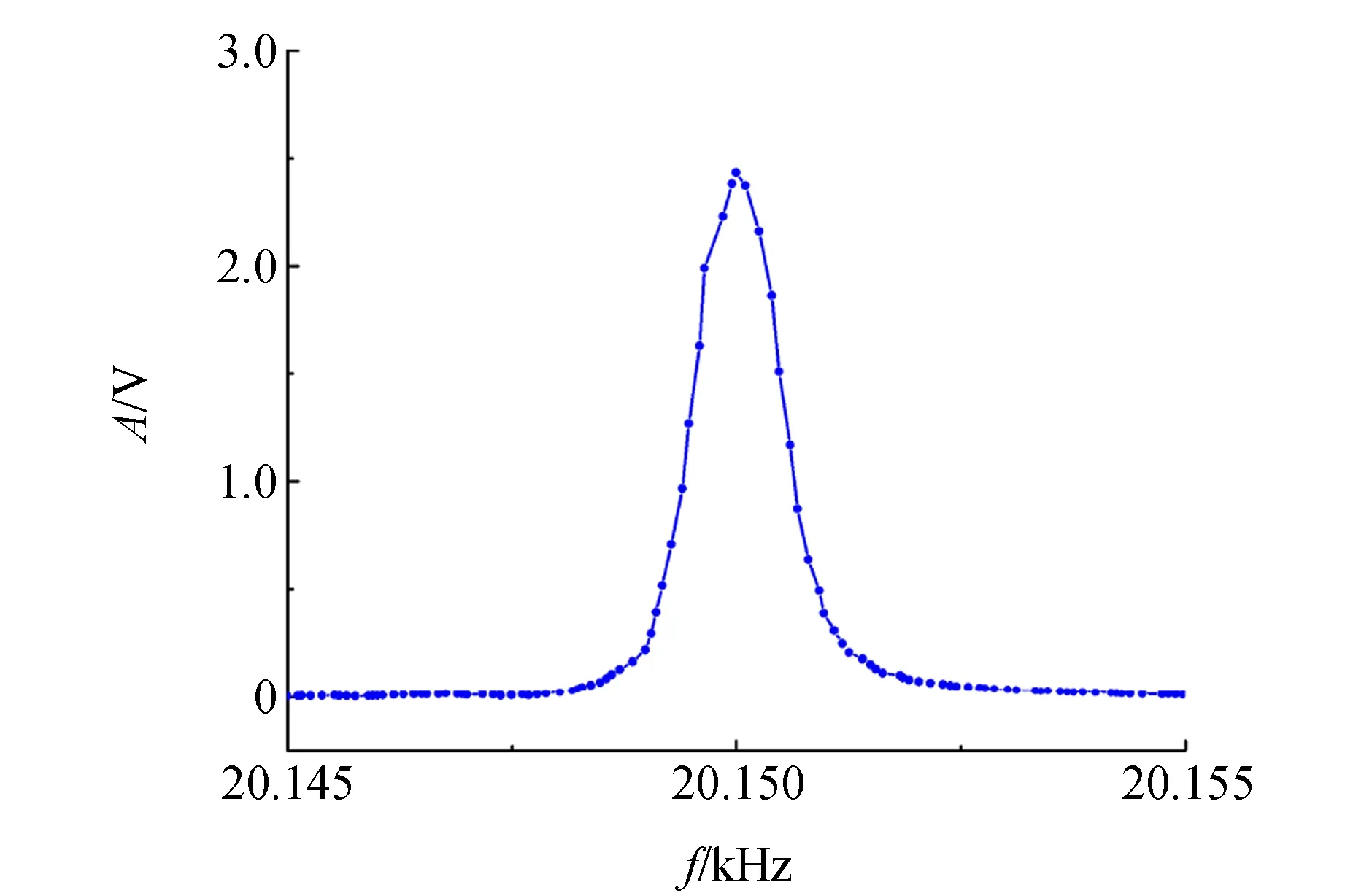
图12 核磁共振稳态吸收

“尾波”是核磁共振弛豫的实验事实[7]. 图13显示经过90°射频脉冲作用且撤除之后，核磁矩处于xy平面绕z轴(即B0方向)进动时，自由感应衰减(Free induction decay, FID)信号在x方向和y方向的投影，两者的相位差π/2. 当忽略B0不均匀性，由FID信号可得横向弛豫时间T2. 若对FID时域信号离散傅里叶分析，可获得共振稳态频域分布[8-9]. 其结果与图12相似，但是可以更准确地描述自旋-自旋相互作用对频域展宽的影响.

图14再次显示图13中FID信号的π/2相位差，更重要的是，它直观地展示了核磁矩M末端在xy平面由外到里的螺线运动轨迹. 有别于图6或经典共振相图，它是同一物理量(响应量)在正交方向的投影，图14结果也反映了由方程(28)所描述的处于外磁场B0中核磁矩M对圆偏振驱动的动力学响应.

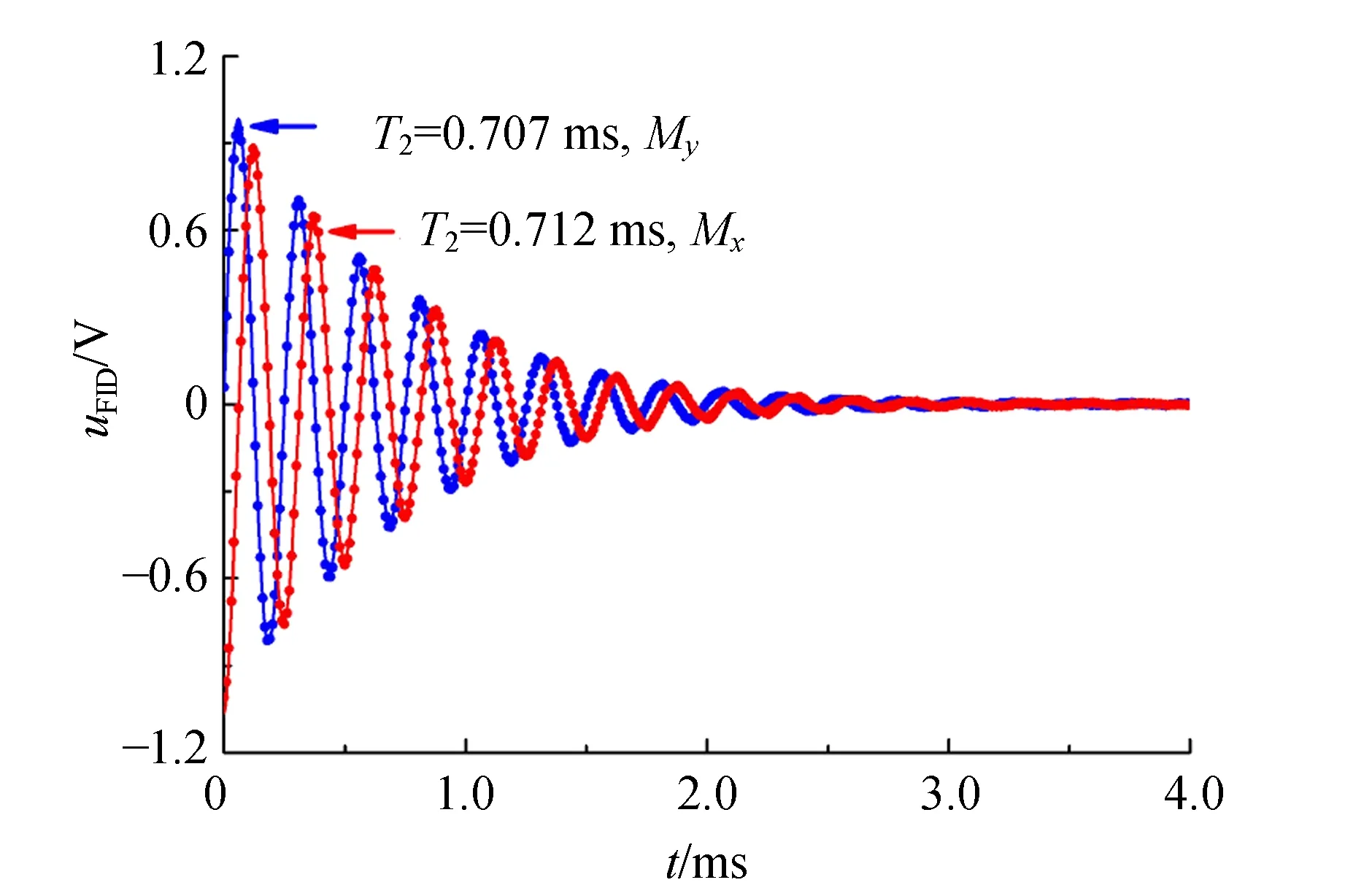
图13 核磁共振横向弛豫FID信号

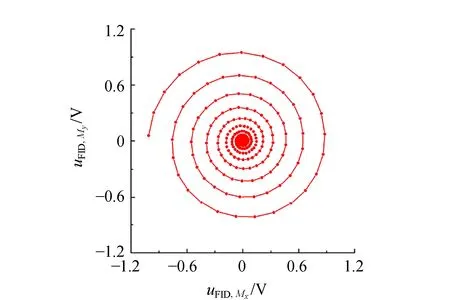
图14 核磁矩末端在xy平面运动轨迹

综合上述分析可知，不管是RLC谐振方程式(6)与式(16)，还是核磁共振方程式(28)，都可由简单受迫阻尼振动方程统一描述，充分说明这些过程存在物理原理共性，其共振频率和阻尼系数(共振弛豫时间)具有相同的物理涵义. 针对不同情形的关键差异体现于：

(33)

1)RLC谐振频率和经典机械共振频率与系统内部损耗有关，而核磁共振频率(即为拉莫频率)与阻尼系数无关；

2)RLC谐振和经典机械共振由线偏振驱动产生，实验上采用线偏振分解实现核磁共振的圆偏振有效激发.

3 结束语

实验事实是物理教学不可或缺的重要基础. 显然，对实验现象深刻理解更有助于透彻讲解物理概念和原理. 核磁共振物理原理和实验技术原理就是很有代表性的物理课程教案. 核磁共振半经典描述与经典振动理论相似，而核磁共振测量则是RLC谐振特性的技术应用. 根据基尔霍夫定律及实验事实的分析表明，RLC谐振特征与经典振动具有相似的物理行为. 另一方面，由布洛赫方程组所得到核磁共振半经典动力学方程与受迫阻尼经典振动方程或RLC谐振方程相似. 由此可见，利用RLC谐振实验物理分析有助于掌握核磁共振原理.