S-型色氨酸生物合成系统的稳态优化
逯 赫,徐恭贤
(渤海大学数学科学学院,辽宁锦州121013)
0 引言
国内许多外学者在色氨酸生物合成系统的单目标优化[1-10]、多目标优化[3,11]、双层优化[12]等方面已经做了很多研究工作,取得了一些成果,使产物色氨酸的产率得到了提高.但目前的研究工作较少考虑色氨酸生物合成系统最优解的稳定性问题,为此,本文拟在S-系统建模框架下,构建稳定性约束条件下色氨酸生物合成系统的稳态优化模型,并为其设计有效的求解算法.本文的研究成果可以为色氨酸生物合成系统的实际操作提供理论指导.
1 色氨酸生物合成的S-系统模型
色氨酸生物合成的S-系统模型可表示为[4,7,9]:
其中,X1、X2、X3和t分别表示无因次的胞内mRNA、酶、色氨酸浓度和时间,i=1,2,3)可表示为[4,7,9]:
2 色氨酸系统的稳态优化问题
基于文献[4,7,9],本文针对S-型色氨酸生物合成系统(1)~(3),构建如下最大化色氨酸产率J,且具有稳定性约束的稳态优化问题:
其中,X=(X1,X2,β1,β2,…,β9)T;第一至第三个约束是稳态约束;(X1,X2,X3)T稳定为稳定性约束条件(i=1,2,3)是基本稳态,这里取
3 优化问题的求解
根据Hurwitz稳定性判别准则[13],优化问题(4)可以转化为如下非线性规划问题:
式中,al >0(l=0,1,2,3),Δk >0(k=1,2,3)为稳定性约束,下面给出其表达式.
首先给出色氨酸生物合成系统(1)~(3)的雅可比矩阵:
然后计算雅可比矩阵J3×3的特征方程:
色氨酸生物合成系统(1)~(3)稳定的充要条件是al >0(l=0,1,2,3),且行列式
的各阶子式Δk >0,即
4 优化结果
非线性规划问题(5)的计算结果如表1所示.从表1中可见,本文获得的色氨酸产率为5.728457.与基本稳态时的色氨酸产率1.310202相比,本文得到的色氨酸产率约为基本稳态时的4.372194倍.
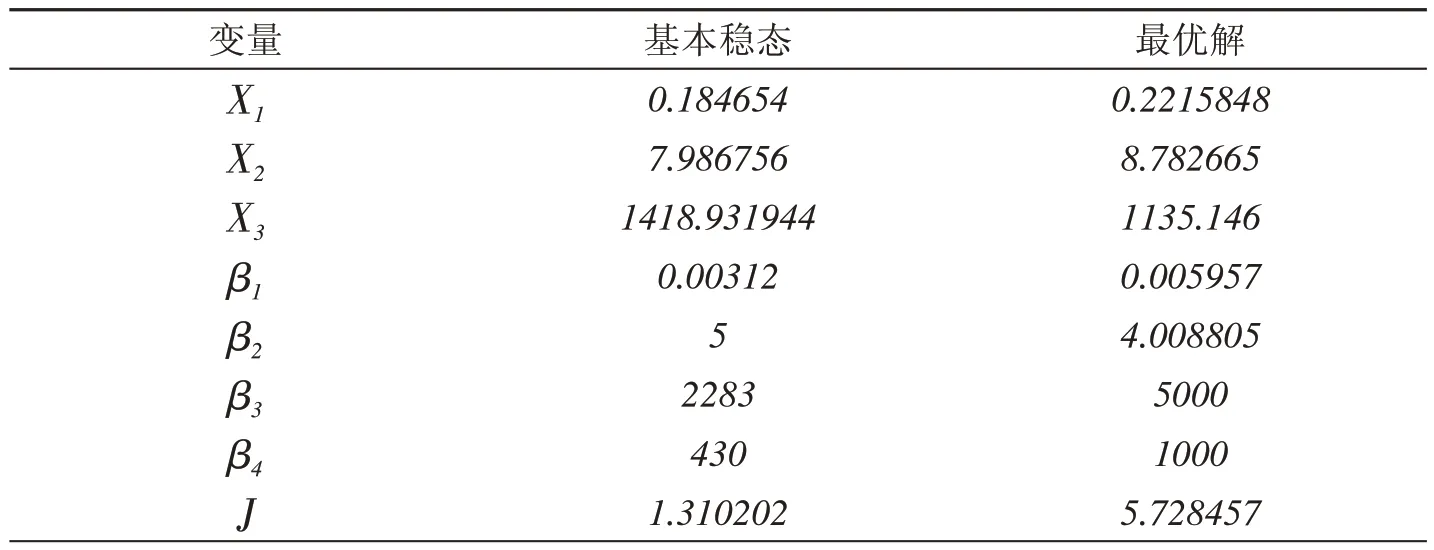
表1 非线性规划问题(5)的最优解
5 结论
本文研究了S-型色氨酸生物合成系统的稳态优化问题.构建了S-型色氨酸生物合成系统的稳态优化模型.应用Hurwitz稳定性判别准则将所构建的稳态优化问题转化为新的非线性规划问题.计算结果表明,本文不仅得到了S-型色氨酸生物合成系统的最优稳态解,而且获得的色氨酸产率约为基本稳态时的4.372194倍.

