微重力下气泡破裂对推进剂贮箱内压力影响的研究

韩兵，孙礼杰，朱曙光，孟绍良

（1.南京理工大学，南京 210094；2.上海宇航系统工程研究所，上海 201109）

推进剂余量测量的准确性是航天器在轨飞行时长的关键影响因素[1]。国内外在微重力下液体推进剂测量方法上提出了体积激励法、簿记法、热容法和PVT 法等一系列方法[2-3]，体积激励法因其精度高、体积小、不受微重力和气液两相混合以及贮箱类型限制等优点[4]具有很好的市场前景。气泡破裂是气液固三相流动中的自然现象，气泡在流场中的运动是一个非常复杂的过程，包含了粘性、可压缩性、热传导、表面张力和接触角等诸多因素[5-6]，气泡破裂会对周围环境产生扰动，贮箱内压力也会因此产生变化，但国内外有关此因素对推进剂余量测量影响的研究较少。本文以体积激励法测量贮箱内部压力流场为研究背景，观察流场中气泡破裂对贮箱内部压力产生的变化，从而探究其对体积激励法测量精度的影响，对微重力环境下液体推进剂余量测量的准确性做了重要补充。

1 体积激励法原理

体积激励法又称压缩测质法，测量原理是体积激励装置进行周期运动，使推进剂贮箱的有效容积产生微小变化，假设液体体积不可压缩，这个微小变化就会对贮箱内气体部分造成影响和改变，测量激励装置周期运动下贮箱内部的压力变化情况便可计算出气体体积参数，由此推算出液体体积，完成贮箱内部推进剂余量的测量。理想状态下的控制方程为：

式（1）中，γ表示为绝热指数，Vg表示为气体体积，P表示为实验环境压力，△V、△P分别表示为体积与压力的变化量。通过进一步计算便可推出推进剂体积，计算公式如下：

式（2）中，Vl、Vt分别表示为贮箱总体积与推进剂体积。

上述公式成立的前提是整个过程处于绝热状态，但是考虑到实际情况下贮箱内部由于漏热会在气液两相间出现传热传质的情况，因此引入平均过程指数k进行修正：

式（3）中，C 表示为传热传质过程的经验常数，f表示为体积激励装置的激励频率。

在体积激励过程中贮箱壁面也会产生变化，会对贮箱内的压力变化造成影响，为更好地探究压力变化与气体体积变化的关系，引入体积变化修正项α进行修正：

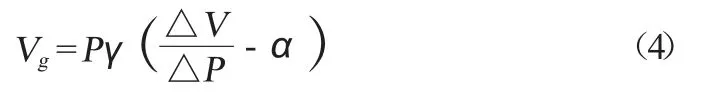
最终修正后的控制方程如下所示：

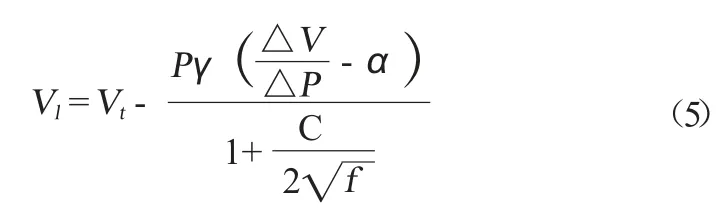
从式（5）可以看出，气泡破裂会造成△P发生变化，进而引起Vl的变化，因此有必要研究气泡破裂对体积激励法测量的影响。

2 数值模型

在微重力环境下，由于密闭环境中存在周期性的体积激励行为，贮箱内的液体会在气液两相界面产生气泡，并且气泡会随着压力的升高而发生破裂，气液两相界面处气泡发生破裂过程的物理机理已经较为成熟。但是实际的气泡破裂情况比较复杂，仅靠一个模型很难概括，所以需要设置一些合理的基本假设以将破裂情况的物理模型简化。

2.1 基本假设

1）贮箱内气体采用理想气体计算；

2）气泡破裂点的位置任意产生；

3）只考虑质量变化与能量变化，忽略动量变化；

4）温度达到对应压力下的饱和温度发生相变，不考虑过热度影响。

2.2 基本方程

贮箱中气体和液体会存在明显的两相分界面，而且气液两相分界面的形状和位置会不断发生改变，对此采用VOF 模型进行描述。VOF 模型中定义所有相的体积分数之和为1，定义第q相的体积分数为αq，那么第q相的连续方程则为：

2.3 相变模型

相变模型分为相平衡与非平衡两种。在相平衡模型中，气相和液相达到平衡时各相间温度相等而且能达到平衡态；在非平衡模型中，两相界面之间存在气/ 液分子的捕获和逃逸行为。基于这两种理论建立流体相变仿真模型，以下是相变传质的理论公式：

相平衡理论相变传质公式：

非平衡传质理论公式Hertz- Knudsen 方程：

影响气液两相界面形状的主要因素为接触角θ、表面张力和惯性力。为得到理想的模拟结果，假设液体对壁面的浸润性良好，设定θ参考值为10o。

3 微重力下气泡破裂仿真模拟

3.1 研究对象

推进剂贮箱仿真模型通过CFD 软件按照1：1 比例建模，采用二维轴对称结构简化模型，为了准确捕捉到多相流中自由相界面的变化情况，采用VOF 多相流模型。

为合理设定液体推进剂在微重力状态下产生气泡的比例，进行贮箱微重力试验，让玻璃罐在高空做自由落体运动以模拟罐内微重力环境，进行试验观察实验现象获取规律。在密闭玻璃罐中分别注入30%、40%和50%液位的液体并使其做自由落体运动，用高速摄像机记录玻璃罐中现象，玻璃罐微重力试验如图1 所示，液体中有生成气泡现象，气泡占比大约为10%。将网格划分为气相和液相两个区域，最终网格数量为23 960，并完成网格独立性验证，保证模拟结果的可重复性与准确性。整体网格质量在0.9 以上，网格模型如图2 所示。

图1 玻璃罐微重力试验

图2 网格模型

3.2 计算方法

模拟采用体积激励法测量推进剂余量，体积激励装置压缩贮箱内气相部分引起其压力产生变化，气体应为可压缩状态，因此选为理想气体。贮箱内液相工质采用高发泡的洗洁精溶液，黏性系数为2 772 mPas。不考虑贮箱壁面发生的传热现象，设置壁面为绝热边界条件。另设置贮箱内初始重力加速度为10-6g，初始温度为300 K，初始压力为101 325 Pa，贮箱初始条件为气液两相饱和状态。

仿真模拟过程中使用欧拉多相流和PBM 模型模拟气泡破裂现象，多相流模型选择Eulerian 模型，欧拉相数量设置为2，液相体积充填率为40%。贮箱内变化过程为非稳态，选择湍流模型为RNGk- e 模型，湍流多相流模型设为混合流。为能准确得到流动后的最终形态，使用显式VOF 模型求解多相流问题。为得到理想状态的气液两相界面，仿真模拟条件中假设液体对壁面的浸润性良好，初始接触角为10°。设置速度压力耦合方式为PISO，设置压力插值等其余项为二阶迎风差分格式。通过动网格来模拟周期性的体积激励过程，选择In- Cylinder 模型，并设定运动边界和运动函数来实现对体积激励过程，与激励装置实际运行工况保持一致，仿真模型中上下运动幅值设为20 mm。网格重构方式设为Smoothing 和Remeshing，这样即使在边界运动时，网格质量也能得到保证。调整时间步长设为1.6×10-4s，这样每个时间步长较小，可以保证计算过程的收敛性。

3.3 仿真结果与分析

在微重力环境下对常压下的充液率为40%的贮箱进行两个完整体积激励周期的模拟，设定液体中生成气泡率为10%，以时间步长为变量记录下体积激励过程中贮箱内的压力云图。时间步长表示激励装置偏心轮的旋转角度，一个时间步长对应旋转角度为1°，因此当时间步长为360 时激励装置完成了一个完整的体积激励周期。微动下体积激励周期不同时刻贮箱内部压力分布云图如图3 所示。

时间步长为90 时，激励装置旋转角度为90°，激励装置向下运动10 mm，气相体积被压缩，贮箱内压力升高；时间步长为180 时，激励装置向下运动20 mm 到达最大位移距离，此时激励幅值最大，贮箱底部压力升高；时间步长为270 时，激励装置往回运动使得气相体积膨胀，贮箱内部压力减小且趋于均匀；时间步长为360 时，激励装置回到初始位置，体积激励过程结束，贮箱内部整体压力分布均匀且压力大小恢复至初始状态，但由于气泡发生破裂所以气相压力有所上升。

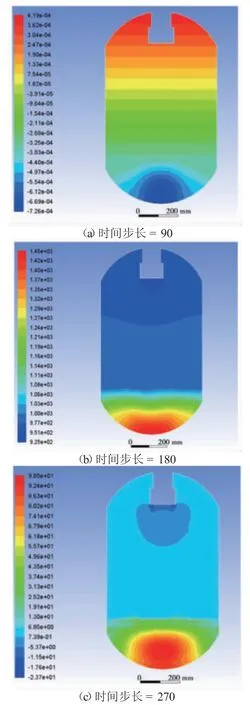
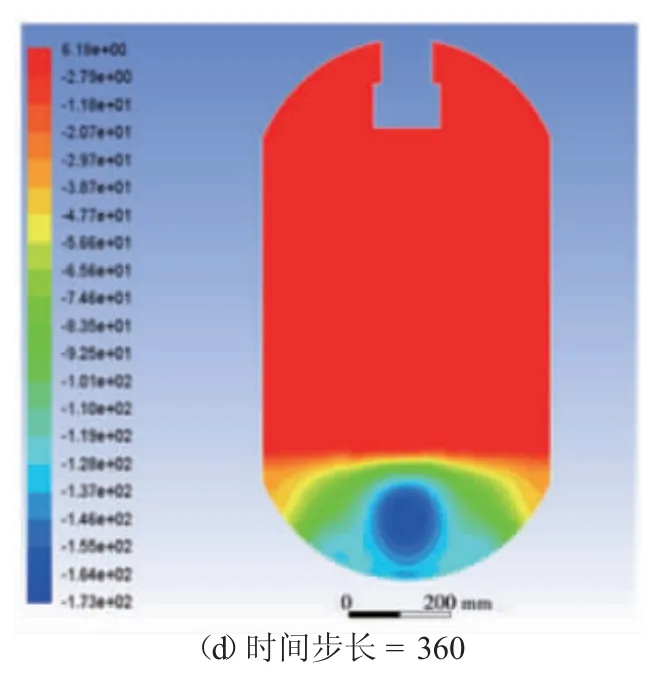
图3 微重力下体积激励周期不同时刻贮箱内部压力分布云图

随着体积激励过程的变化，贮箱内的压力也在不断变化，微重力下气相压力动态模拟曲线如图4 所示。由于气泡发生破裂，激励周期结束后的气相压力比初始压力稍微升高了一些。

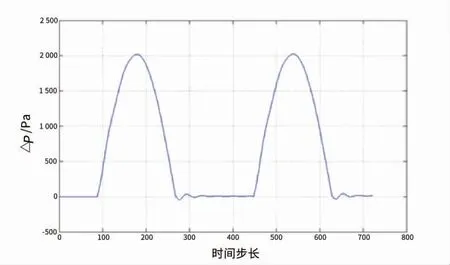
图4 微重力下气相压力动态模拟曲线

在贮箱充液率为40%的条件下，改变气泡生成率和静压条件，对10%、50%和90%的气泡含量以及0.1 MPa、0.2 MPa和0.3 MPa 压力下所有的组合工况进行仿真模拟，得到贮箱压力动态变化曲线如图5 所示。

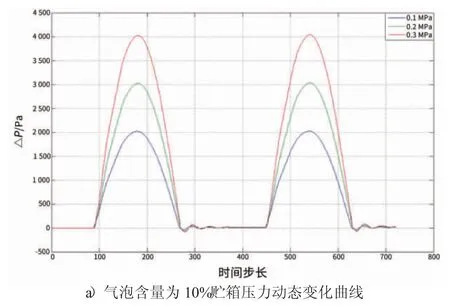
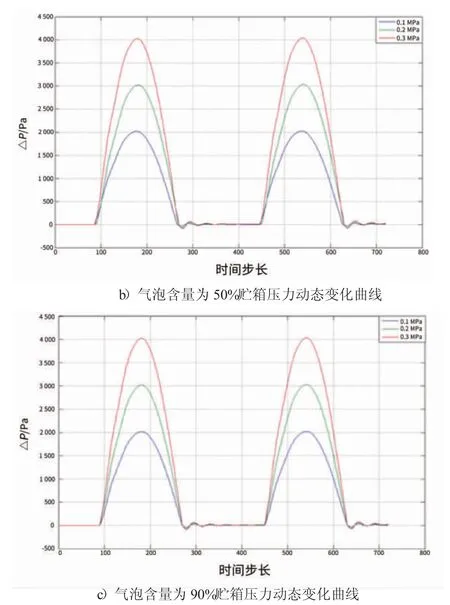
图5 贮箱压力动态变化曲线

为探究气泡破裂对贮箱内压力的影响，需要将气泡破裂前后贮箱内压力变化的情况进行对比，因此对不考虑气泡破裂因素贮箱内压力动态变化进行模拟研究，得到结果如图6所示。从图5 和图6 的对比中可以看出，多种工况下气泡破裂后贮箱内压力动态变化曲线与气泡破裂前贮箱内压力动态变化曲线变化规律基本一致。

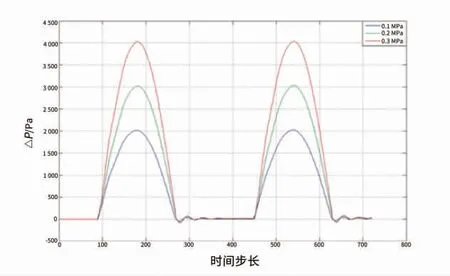
图6 不考虑气泡破裂贮箱压力动态变化曲线

对贮箱模拟两个周期的体积激励过程，从各工况下贮箱内压力动态变化曲线中可以看出，在两个周期内贮箱内部气相压力均存在稳定峰值，将各工况下气泡破裂前后贮箱内气相压力变化进行对比，得出气泡破裂对体积激励法的测量误差，气泡破裂引起体积激励法的测量误差如表1 所示，两组实验次数依次对应两个周期。结果表明：各工况下气泡破裂引起的体积激励法的测量误差都在0.1%以内，证明微重力下气泡破裂对推进剂贮箱内压力变化造成的影响较小，体积激励法依然合理可行。

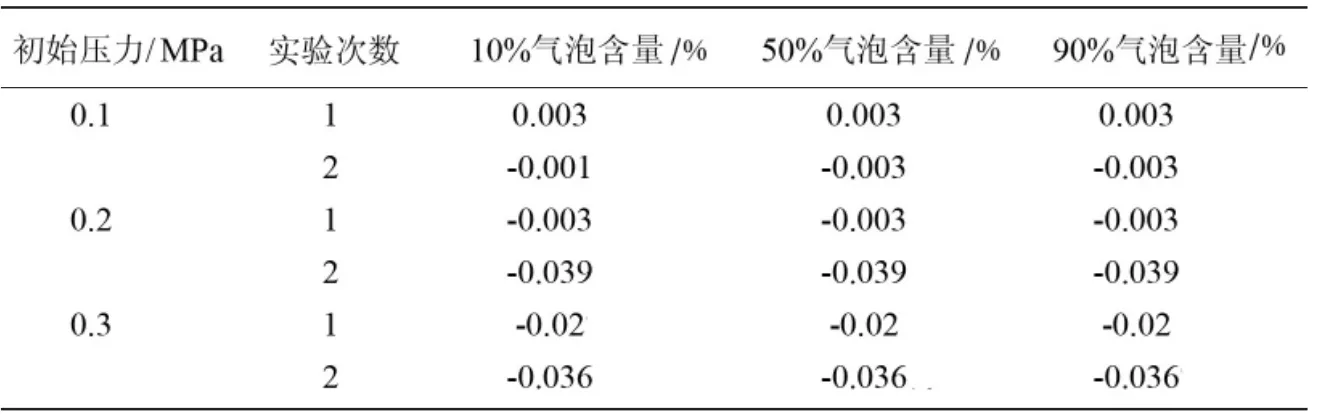
表1 气泡破裂引起体积激励法的测量误差

4 结语

本文在体积激励法的基础上，对微重力下贮箱内液体中的气泡破裂对贮箱内部压力稳定性造成的影响进行了研究。以贮箱为研究对象，在fluent 软件上建立仿真模型，观察贮箱内部气泡破裂后气相压力动态曲线，从而研究气泡破裂引起对体积激励法测量误差。经过分析，得到以下结论：

对于任意工况下的实验模拟贮箱，气泡破裂后其内部的气相压力均存在稳定的峰值，与相同工况下不考虑贮箱内发生气泡破裂时气相压力的峰值进行对比，随着压力的不断增大，误差也有所增大，但所有误差均在0.1%范围内，证明微重力下气泡破裂对体积激励法的测量影响较小，体积激励法依然合理可行。