弹体撞击位置对加筋板毁伤特性的影响

赵 健

(海军装备部驻上海地区军事代表局驻上海地区第五军事代表室，上海 201913)

对于大型船舶舷侧结构冲击问题，由于舷侧结构几何尺寸较战斗部的直径以及其塑性并行区域大得多，因此在分析中可以将其考虑为无限大的板壳结构。它在冲击载荷作用下的碰撞损伤过程是复杂的非线性动态响应过程，既有结构发生大位移时所产生的几何非线性，又有材料发生大变形时所表现出的物理非线性(材料非线性)，还存在严重的运动非线性，同时还包含复杂的接触和摩擦问题[1]。

对于弹体穿甲现象有经验法、半解析法、解析法和数值法4类处理方法。朱锡等[2]进行了防半穿甲弹体战斗部动能穿甲的模拟试验研究；朱建方等[3]研究了反舰弹体动能穿甲效应中倾角的影响。本文的研究也是目前船舶碰撞冲击研究的一个重要内容。

1 薄板穿甲的一般计算方法

薄板穿甲算法的基本目的是处理2个含侵彻单元的接触体间的相互作用。侵彻单元是在计算过程中由于高应变而毁伤的单元，即它们在入射体和目标相互作用的问题中失效。当一个单元被侵彻时，它所有的应力变量设置为0，但与该单元相关的节点保持其质量和动量。

薄板穿甲的有限元算法使用从节点和主单元来进行，2个接触体中的入射体通常定义为节点(以下称为从节点)，第二个接触体定义为单元(以下称为主单元)。如果从节点位于主单元中，则它被移到接触面的外部，为了确定外表面，一系列法向量装配给所有的主单元。由于装配过程的特征，非0向量只在外表面产生结果，并向该表面提供有效平均水平。

2个接触体的相互作用机理完全通过从节点和主单元的相互作用来执行。相互作用准则如下：①从节点不允许穿透主单元；②当探测到从节点穿透主单元时，从节点通过投影到其穿过的单元表面而返回，相关动量转移到主单元的合适节点。如果检查表明投影没有将从节点移动到外表面，则从节点移动到了合适的单元边界。

该程序的有效性在很大程度上取决于显式时间积分的使用，显式求解是对时间进行差分，不存在迭代和收敛问题，最小时间步取决于最小单元的尺寸。出于稳定性需求，需要限制时间步，以便于被穿透的主单元有效代表相互作用区。荷载步用来施加一个阶段的力，荷载子步是为了计算结果而把荷载步分成许多小的子载荷步。子载荷步和时间步是相对应的。最小时间步是为了既满足计算精度又提高计算效率，让计算机得以在一定范围内选择时间步的大小。需要注意的是，在高速冲击情况下，内表面从节点时间步必须被限制，使从节点在一个时间步的移动不大于10%～20%的区域尺寸。由于三维仿真中涉及到的从节点和主单元数量很大，所以需要特殊技术来快速确定在其中间能发生相互作用的从节点和主单元。这可以通过使用固定在空间中的结构单元来完成。一般认为结构单元从客观上大于网格单元，所以可以包括很多主单元和从节点。程序的基础是确定结构单元中所有的从节点，然后处理位于结构单元中的网格单元数量，并检查在相互作用中占用相同结构单元的从节点。

2 计算模型

2.1 几何模型

取战斗部直径为0.36 m，总质量为165 kg，舷侧面板厚度为0.02 m，采用面板纵、横向都有加强筋的形式，加强筋与面板采用同种材料，加强筋的厚度为0.02 m、高度为100 mm、间距为1 m。由于船舶舷侧尺寸比战斗部的直径大很多，而撞击过程中舷侧板塑性作用区域通常在2～3倍弹径范围内，在仿真计算中，舷侧面板的平面尺寸取3 m×3 m，边界条件为固支边界。为减少边界条件和非对称情况所造成的影响，针对撞击点在战斗部与加强筋不接触、战斗部与1个方向加强筋相接触、战斗部同时与2个方向加强筋相接触3种不同的撞击区域的情况进行仿真计算时，分别对应选择工况1、工况2、工况3的3种舷侧板模型，如图 1所示。在针对每种舷侧板模型进行仿真计算时，撞击点的位置取在该舷侧板的中心。

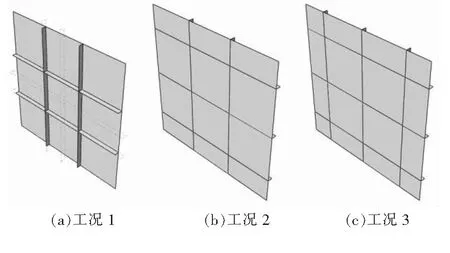
图1 舷侧板模型

2.2 有限元模型

使用Abaqus软件进行舷侧板结构建模，单元类型为S4R(4节点双曲线缩减积分沙漏控制有限膜应变厚/薄壳单元)。以工况3为例，研究对象的有限元模型如图 2所示。

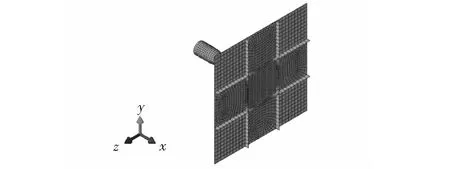
图2 研究对象的有限元模型

一般来说，钢结构具有应变硬化正切模量Et，其典型取值范围为杨氏模量(E)的5%～15%。文中使用的材料为Q345B钢，其E为2.1×105MPa，泊松比为0.28，屈服强度σs为345 MPa，应变硬化正切模量Et为E/65。显然应变硬化对加筋板的非线性行为有一定影响。影响的程度是包括板长细比在内的众多因素的函数。在本文中，板的应变硬化正切模量的值是Khedmati[4]通过大量弹塑性大变形分析得到的，材料的理想弹塑性应力-应变行为如图 3所示，其中εY为屈服应变，σY为屈服应力，εY=σY/E。边界条件为固支边界，初始速度v1=450 m/s，。

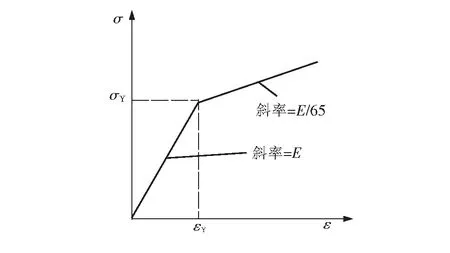
图3 材料的理想弹塑性应力-应变行为

3 弹体穿甲过程的数值模拟

3.1 弹体末速度与加筋板破口

战斗部穿透舷侧板时的形状如图4所示，战斗部的速度随时间变化如图5所示。当小锥头弹丸穿过塑性较好的薄靶时，弹丸很快穿透靶板，随着弹丸前进，靶板沿着弹丸表面扩张而被挤向四周，主要是径向扩张变形，轴向伸长可以忽略不计。

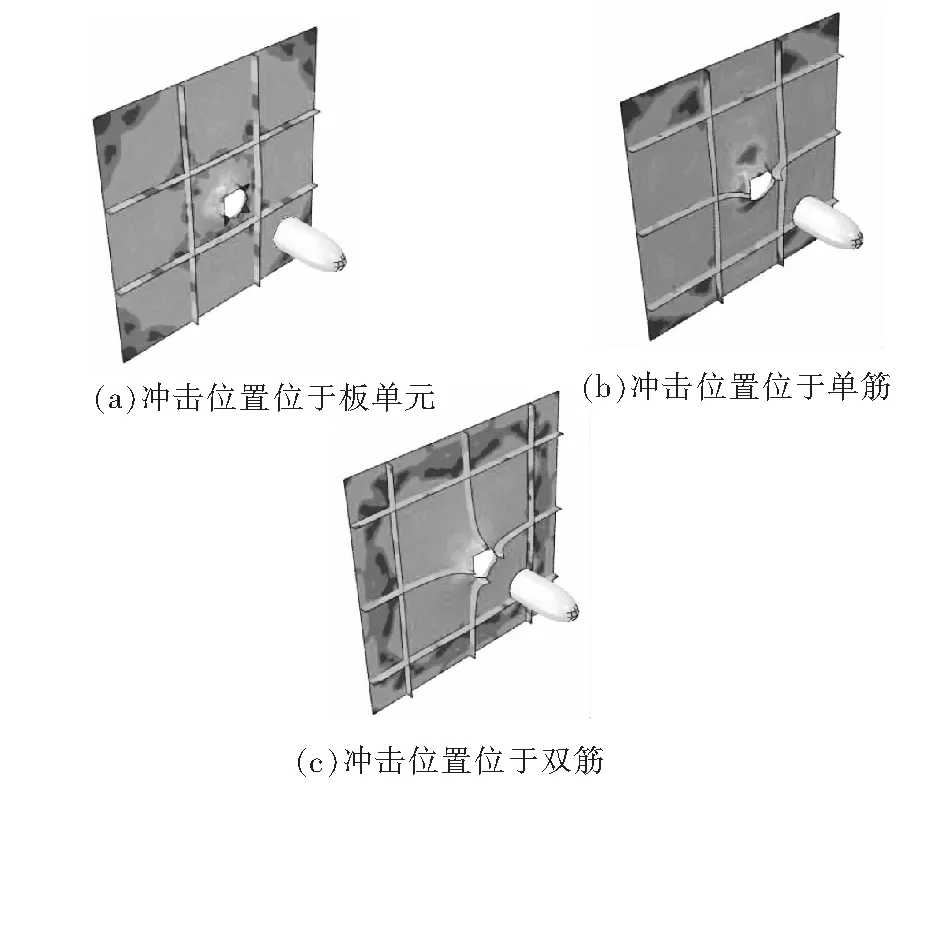
图4 战斗部穿透舷侧板时的形状

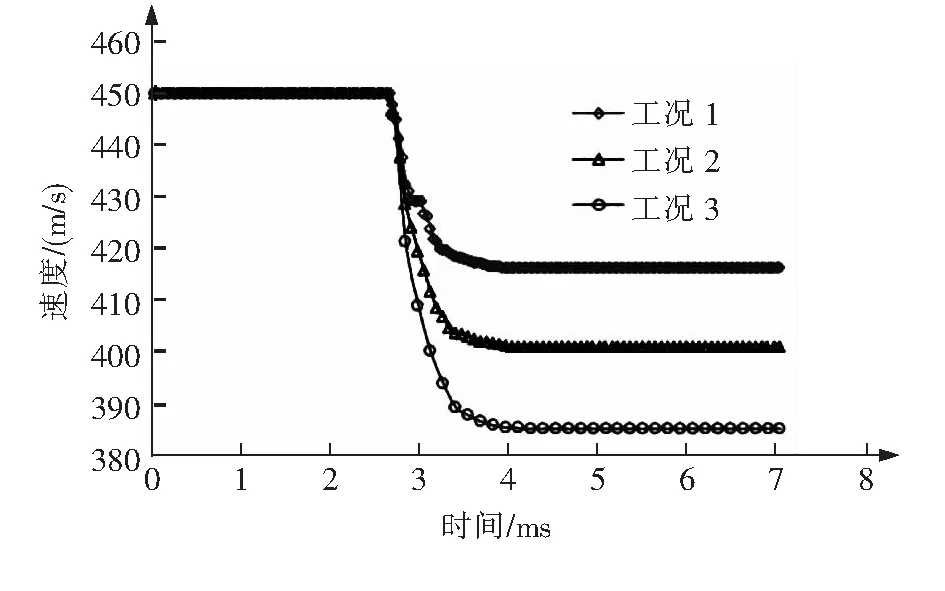
图5 战斗部的速度随时间变化

由图5可知,3种工况下的穿透末速度分别为416 m/s(0.92v1)、401 m/s(0.89v1)、385 m/s(0.86v1)，即当战斗部与加强筋不接触时，剩余速度最大，而战斗部同时与2个方向加强筋相接触时，剩余速度最小，这是因为与战斗部接触的加强筋越多，加筋板局部区域吸能越多，这与客观事实是相符的。

3.2 能量与接触力

3种工况下,模型动能和内能随时间变化分别如图 6、图7所示。3种工况下弹体动能的损失分别为2.10×109J、2.95×109J、3.80×109J，内能增加分别为1.63×109J，2.43×109J，3.21×109J。可以看出，在碰撞过程中，模型动能的大部分转化为内能，只有一小部分以其他形式散发出去。

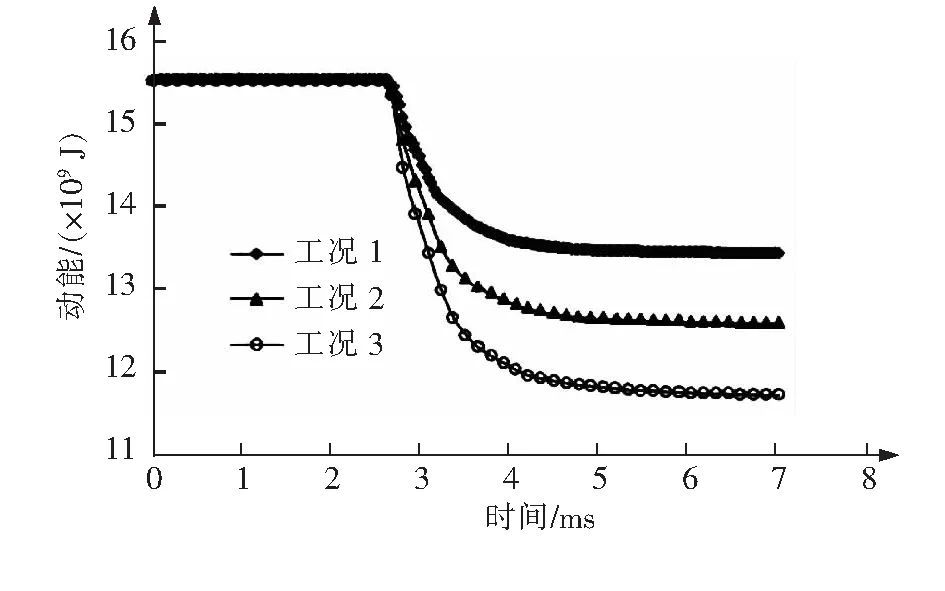
图6 模型的动能随时间变化

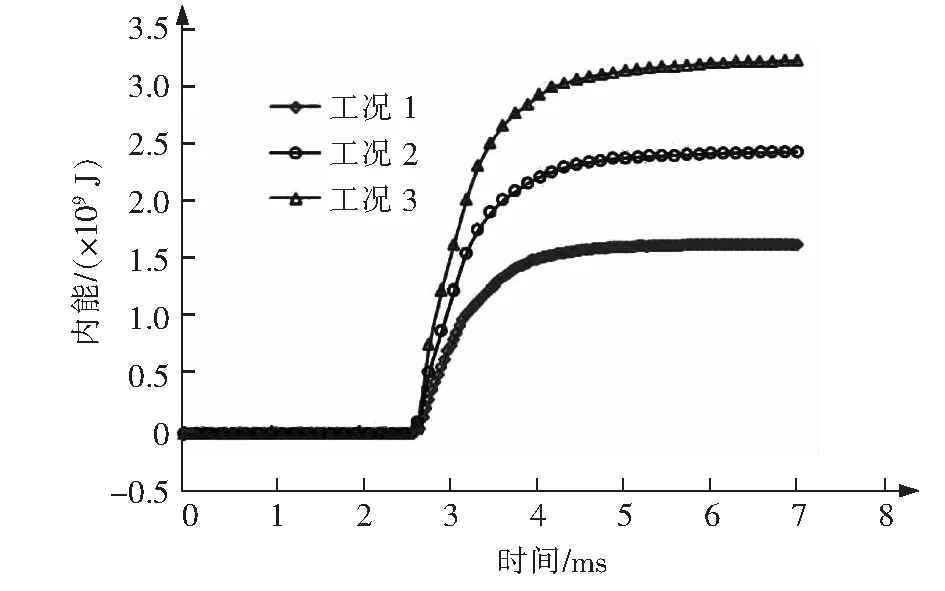
图7 模型的内能随时间变化

3种工况下,模型x方向和z方向接触力随时间的变化分别如图8、图9所示。对于x方向的接触力，3种工况下的最大值都发生在第2.7 ms(弹体开始与加筋板接触时)，最大值分别为2.22×107N、2.78×107N、2.86×107N；对于z方向的接触力，3种工况下的最大值分别发生在第3.47 ms、4.13 ms、3.47 ms，最大值分别为734 kN、948 kN、576 kN。可以看出，碰撞过程中的接触力的变化范围比较大，对于结构有较强的破坏性。

4 结束语

本文介绍了薄板穿甲的一般计算方法，建立了弹体穿甲的有限元模型，对弹体穿甲过程进行了数值模拟，得到了弹体末速度、加筋板破口、能量、接触力随时间的变化关系，对比了弹体不同撞击位置对加筋板毁伤特性的影响。根据本文的研究，得到如下结论：①与战斗部接触的加强筋越多，加筋板局部区域吸能越多，弹体末速度越小。②在碰撞过程中，模型动能的大部分转化为内能，只有一小部分以其他形式散发出去。③碰撞过程中的接触力的变化范围比较大，对于结构有较强的破坏性。

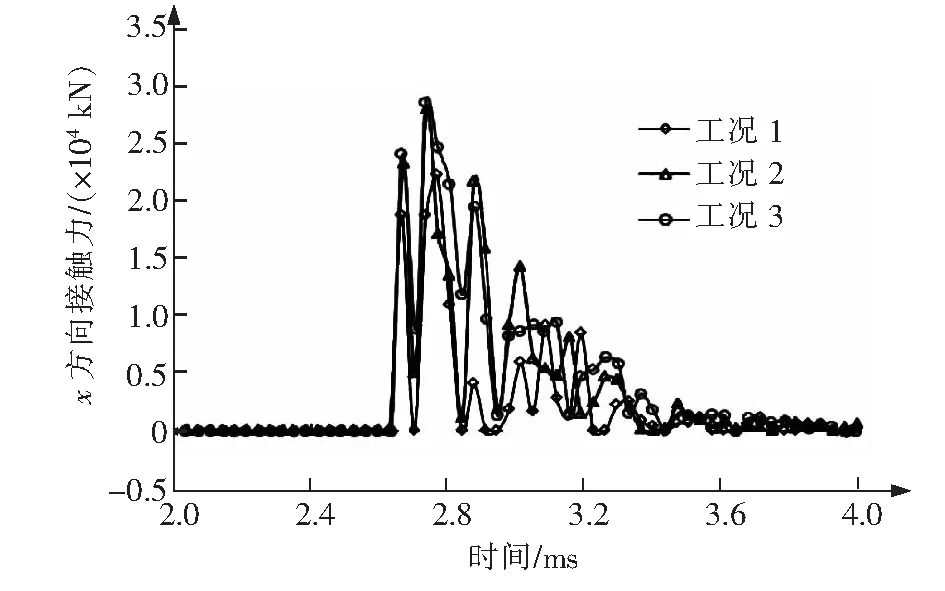
图8 x方向的接触力随时间变化

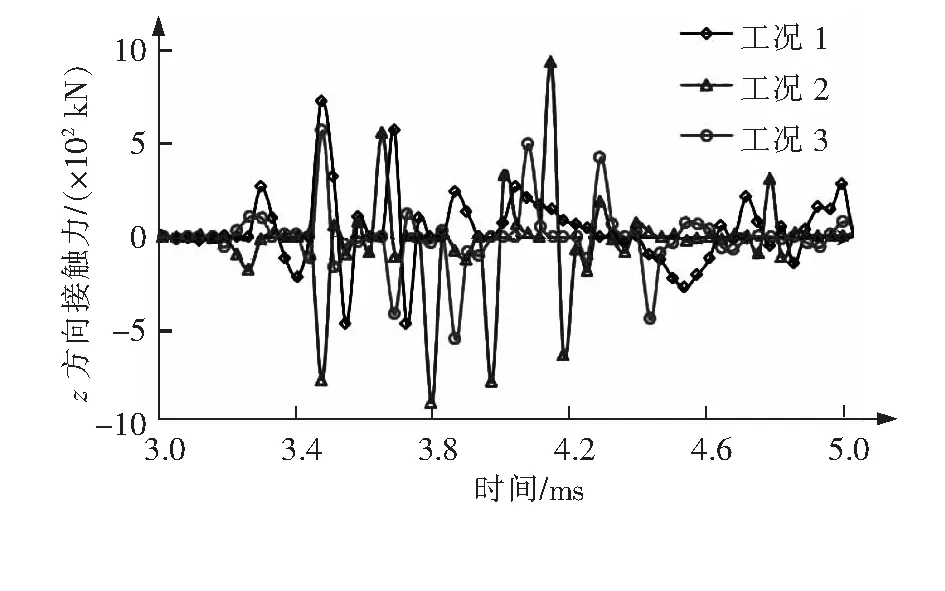
图9 z方向的接触力随时间变化