模拟退火自适应反向无惯性粒子群优化算法

曹文梁, 康岚兰, 王 石

(1.东莞职业技术学院 计算机工程系,广东 东莞 523808; 2.江西理工大学 应用科学学院,江西 赣州 341000)

0 引 言

粒子群优化(particle swarm optimization,PSO)算法是文献[1]在研究鱼群及鸟类等群体觅食行为的过程中提出的一种随机仿生进化算法。由于其概念简单且易于实现,自提出以来,受到科研人员广泛关注,也是目前应用最为广泛的一种进化优化算法,PSO已在智能交通、制造、生物科学、国防等多个不同领域取得了良好的应用效果[2-6]。

然而,PSO从设计之初就伴随着收敛速度过慢、易陷入局部最优、参数依赖过大等问题。为加快PSO收敛速度,科研人员将反向学习策略引入到PSO中,并对反向策略中关键参数展开详细研究,给出取值建议。然而,理论与实验分析表明,反向策略的引入虽然加快了粒子群的收敛速度,但同时提高了粒子陷入局部最优的概率。

为解决上述问题,本文提出了一种模拟退火自适应反向无惯性粒子群优化(simulated annealing adaptive opposition-based non-inertial particle swarm optimization,SAONPSO)算法,该算法一方面从参数调节角度出发,对反向策略展开研究,受模拟退火思想(simulated annealing, SA)[7]启发,提出了一种自适应退火策略调节反向策略使用概率;另一方面提出一种精英差分变异策略,避免粒子陷入局部最优;除此之外,为降低参数控制对算法的影响,引入一种无惯性速度更新公式取代标准PSO算法速度更新公式,最终达到高精度快速收敛的目的。在11个典型测试函数上采用多种基于反向学习PSO算法进行仿真实验，结果表明, SAONPSO算法在大部分函数上取得最优解的同时,收敛速度得到了显著提高。

1 反向PSO算法

1.1 标准PSO

PSO算法[1]是一种群智能随机进化算法,群体中每个粒子表征问题的一个候选解,在解空间中,粒子根据如下动力方程搜索最优解,即

vi,j(t+1)=ωvi,j(t)+c1rand1(pbesti,j-xi,j(t)) +c2rand2(gbestj-xi,j(t))

(1)

xi,j(t+1)=xi,j(t)+vi,j(t+1)

(2)

其中,vi,j(t)、xi,j(t)分别为t时刻第i个粒子在第j维上的速度与位置分量;pbest、gbest分别为粒子当前最优位置和粒子群全局最优位置;i=1,2,…,N;j=1,2,…,D(D为空间维度,N为粒子群规模);ω∈[0,1]为惯性权值;c1,c2∈[0,2]分别为认知学习因子和社会学习因子;rand1、rand2分别为[0, 1]区间上服从均匀分布的随机数。

1.2 一般化的反向学习策略

文献[8]首次提出反向学习(opposition-based learning,OBL)策略,目前已应用于多种优化算法中。其主要思想是:同时评估一个可行解及其反向解,将其中较优解保留进入下一代进化。

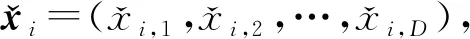
(3)

其中,k∈U(0,1)的随机数;[da,db]为搜索空间的动态边界,且每一维取值为:

daj=min(xi,j),dbj=max(xi,j)

(4)

(5)

使用反向策略的PSO算法称为反向粒子群优化算法。根据文献[9]的分析,粒子在每一代的进化中,GOBL策略使用概率取0.3时结果普遍较优。

2 精英差分变异策略

由(1)式可见,粒子飞行方向受群体当前最优位gbest的引导,为降低粒子陷入局部最优的可能性,本文视gbest为种群精英粒子,受差分演化思想的启发,对其在每一代中进行变异操作,从而提高算法全局探索能力。该变异策略称为精英差分变异策略(elite differential evolutionary mutation,EDEM),具体公式为:

(6)

其中,r1、r2、r3、r4∈[1,N]为互不相等的随机整数;F为尺度系数。

SAONPSO算法如下:

随机初始化含N个粒子的种群P,根据(3)～(5)式获得N个粒子的反向粒子,构成其反向种群OP,计算种群P∪OP中每个粒子的适应值,选择其中较优的N个粒子作为初始种群P;

While未达到终止条件时do

根据(9)式生成GOBL策略概率jr;

If rand(0,1)

根据(3)～(5)式更新OP,在解空间P∪OP中选取N个适应值占优的粒子;

更新 pbest 和 gbest;

else

fori=1 toNdo

根据(2)式、(7)式,获得第i个粒子的速度与位置向量,并更新粒子适应值;

更新pbest和gbest;

end for

end if

forj=1 toNdo

对当前gbest 根据EDEM变异公式(6)式进行变异操作;

end for

iff(gbest*)优于f(gbest) then

用gbest*位更新当前gbest位;

end if

end While

3 无惯性速度更新公式

由标准PSO速度更新公式(1)式可见,粒子飞行方向受惯性动力、认知学习和社会学习3个项引导,文献[9]指出,虽然惯性项使得粒子群保持了种群多样性,但它同时也降低了粒子群的收敛速度。为进一步增强种群局部开发能力,提高粒子群收敛速度,本文引入一种无惯性速度更新公式(non-inertial velocity update formula, NIV)(7)式取代(1)式引导粒子飞行方向,即

vi(t+1)=s(u(t)-u(t-1))+

c1rand1(pbesti-xi(t))+

c2rand2(gbest-xi(t))

(7)

其中,s∈(0,1)为差分系数(differential coefficient),用于控制种群搜索范围,根据文献[12]的分析,当s取值在0.1～0.2之间,性能普遍达到最佳,因此本文后续实验中取s=0.1;u(t)、u(t-1)分别为种群在t时刻与t-1时刻所有粒子位置均值,即第j维上取值公式为:

(8)

4 SAONPSO算法

本文将EDEM策略与NIV速度更新公式应用于反向学习PSO算法中,给出了SAONPSO算法，用伪码描述了SAONPSO算法的基本步骤，其中变量jr为使用GOBL策略的概率。文献[9]仿真实验分析表明,当jr取0.3时性能较好。然而固定反向策略使用概率并不是一个好的选择,本文采用SA算法根据粒子在不同阶段的需求自适应选择反向策略使用概率,即

(9)

其中,u(t)、u(t-1)分别为粒子群在迭代第t代与t-1代所有粒子位置均值;f(u(t))、f(u(t-1))分别为其对应均值位适应值。易知,jr越小,粒子收敛速度越高,然而,当种群内粒子越聚集时,粒子陷入局部最优的可能性越大,此时,反向策略使用概率jr取值增大。可使得粒子避免陷入局部最优。

由SAONPSO算法步骤可知,SAONPSO算法主要包含初始种群、GOBL策略、速度与位置更新操作、EDEM变异操作4个部分。其中,速度与位置更新操作的时间复杂度易知为O(N);初始种群包括个体随机生成、反向解生成及种群选择机制3个部分,GOBL策略中包括反向解生成和种群选择机制部分,其中随机个体生成和反向解生成时间复杂度均为O(N·D),而种群选择操作的复杂度为O(N2)。然而,GOBL策略中,若维度D较小,群体规模N可近似于D;反之,D较大时(D≥100),N通常小于D;因此,GOBL策略计算复杂度可计为O(N·D)。综上所述,SAONPSO算法的计算复杂度也可计为O(N·D)。

5 数值仿真实验及分析

(1) 算法性能测试。SAONPSO算法与5种基于反向学习的PSO(OBL-based PSO)进行比较,它们分别是OPSO-AEM&NIW[13]、OPSO[14]、GOPSO[5]、OVCPSO[15]和EOPSO[16]。实验中,为确保对比的公平性,所有算法种群规模N均取40,其他参数保持与原文献一致。

(2) 策略分析。分析EDEM和NIV 2种策略,以及自适应反向策略使用概率jr的使用对算法的影响。

(3) 参数敏感性分析。分析种群规模取不同值时,对算法性能的影响。

SAONPSO算法默认参数设置见表1所列。特别地,除SAONPSO算法外其他反向PSO算法jr取值均为0.3。

表1 SAONPSO算法参数设置

5.1 实验设置

数值实验中使用的11个测试函数见表2所列。按其属性分为单峰f1～f4和多峰f5～f11两大类,其中多峰函数包括简单多峰函数f5～f7，带旋转的多峰函数f8、f9和移位多峰函数f10、f113种。为使所有测试函数在零点位均取得全局最优值0,本文参考CEC 2010中的函数定义,将移位多峰函数中的参数f-bias统一设定为0。表2中,M为D×D随机正交矩阵;o为D维随机位移向量。

表2 数值实验中使用的11个测试函数

5.2 实验结果与分析

5.2.1 算法对比分析

对比实验中,6种反向PSO算法最大迭代次数均为10 000,每个测试函数均运行30次,全局最优值的均值见表3所列。实验采用双尾t检验对结果进行显著性差异统计分析,显著水平为0.05。表3中,“-”、“+”、“=” 3种符号分别表示SAONPSO算法的性能劣于、优于、相当于其他5种对比算法。

从表3可以看出,SAONPSO在6种算法中是较优的。其中相比OPSO和OVCPSO,在所有测试函数上均取得显著优势;虽然在与EOPSO算法的对比中,在f3测试函数中结果较劣,但在其他9个测试函数上均取得最优。另外,SAONPSO除f11外,均优于或相当于GOPSO结果。特别地,OPSO-AEM&NIW和SAONPSO在大多数函数中取得了相当的最优解,但在3个测试函数f3、f5、f11上,SAONPSO优于OPSO-AEM&NIW。

为进一步比较OPSO-AEM&NIW和SAONPSO性能上的差异,2种算法在求解精度为10-16、最大迭代次数为10 000次、统计适应值函数评估次数(FES)相同条件下,在11个测试函数上取值函数评估次数比较结果见表4所列。表4中，Fval为函数值。由表4可知,SAONPSO在所有测试函数中,FEs均显著小于OPSO-AEM&NIW,由此可见,SAONPSO显著提升了反向PSO的收敛速度。

表3 OPSO、GOPSO、OVCPSO、EOPSO OPSO-AEM&NIW和SAONPSO算法在11个测试函数上的结果均值

表4 OPSO-AEM&NIW和 SAONPSO算法在11个测试函数上取值函数评估次数比较

5.2.2 策略有效性分析

SAONPSO算法将EDEM和NIV 2种策略融入到GOBL之中,对OBL-based PSO算法进行了改进。为分析2种策略对算法性能所产生的影响,本文以测试函数f2、f6为例,分别将EDEM、NIV与GOBL进行组合,即GOBL+EDEM、GOBL+NIV与改进算法SAONPSO(GOBL+EDEM+NIV)作对比实验,GOBL+EDEM实验中,惯性系数ω取固定值0.729 84[14]。EDEM、NIV 2种策略对算法的影响如图1所示。实验结果表明:NIV策略充分获取环境信息,利用前2个时刻种群信息差值,指导粒子下一时刻的飞行方向,有效加快了粒子群的收敛速度;EDEM策略则通过对精英粒子(gbest)的扰动,降低粒子陷入局部最优的概率,确保粒子群平滑且快速地收敛到全局最优值。

图1 EDEM、NIV 2种策略对算法的影响

5.2.3 参数敏感性分析

为检验SAONPSO算法对粒子种群数目N取值敏感性,本节以测试函数f2、f6为例,在种群规模N分别取20、40、60、80、100的5种情况下对算法展开进一步的仿真实验,N取不同值时SAONPSO算法全局收敛过程如图2所示。由图2可知,当N取值较小(<40)时,算法可能在未取得最优值时停沚或需较大开销才能收敛到最优值;当N取值较大(>60)时,虽然算法能取得最优值,但可能需要花费更大的开销;而种群规模在40～60之间,算法普遍能以较快的收敛速度取得最优值。

图2 N取不同值时SAONPSO算法全局收敛过程

6 结 论

本文提出了SAONPSO算法。该算法将EDEM策略和NIV融入到GOBL中,使得反向粒子群优化算法在加强空间探索能力的同时,有效避免陷入局部最优,使算法收敛速度得到显著提高。除此之外,本文在GOBL基础上,根据粒子进化不同阶段的收敛特性,提出了一种自适应选择反向策略使用概率的方式取代了取固定值的方法,进一步避免粒子出现早熟现象。多种测试函数仿真实验结果表明,新算法在获得高精度解的同时,显著提高了算法的收敛速度。

下一步将对算法性能展开理论分析,并将其应用于高维问题中验证算法有效性。将算法与实际问题相结合进行研究是未来工作的重要方向。