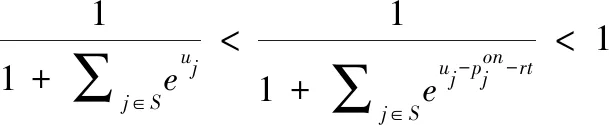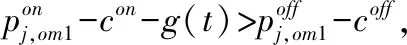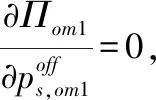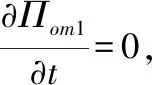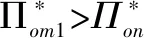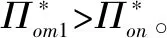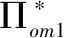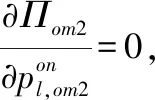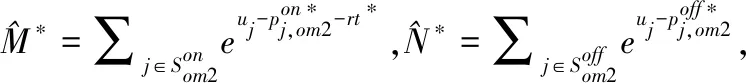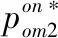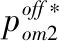消费者导向类型与电商全渠道决策研究
郎 骁,邵晓峰
(上海交通大学安泰经济与管理学院,上海 200030)
1 引言
随着零售业的发展,很多电商通过开设实体店抢占线下资源。如当当2015年底宣布在3-5年内开1000家实体书店,截止2017年中已开业书店共145家,为全国1.3亿当当会员提供丰富的线下文化服务[1]。与此同时,2017年4月,京东宣布未来五年将在全国开设100万家京东便利店,三年内还将在全国开设5000家“京东母婴体验店”[2]。截止2017年8月,京东已经在线下开设了92家门店[3]。
当当网和京东商城作为成功电商的代表,曾经都凭借线上渠道的成本和规模优势,冲击了各自所在市场的实体店经营,改变了市场格局。在经历了市场份额的增长后,却进入曾被认为不占优势线下渠道,说明越来越多的电商开始注重开拓线下市场,努力满足不同种类消费者的需求,从而在市场竞争中占据先机。但电商进入线下渠道也存在风险。据《北京商报》报道,2016年8月一加手机正式宣布将关闭位于北京、上海两地的一加手机旗舰店,此次两家最后的旗舰店关闭,也意味着一加手机在国内的线下自营渠道不复存在[4]。
上述例子说明电商需注重线下渠道的开拓,满足不同种类消费者的需求,进而在市场竞争中占据优势;但进入线下渠道也需充分考虑消费者的选择行为和市场情况,避免亏损。
本文研究电商在面对不同消费者导向类型时,是否应采取全渠道决策(即进入线下渠道),及如何做出各渠道产品组合、价格和交付时间决策。文献综述从单渠道零售商的全渠道决策和产品组合决策角度展开。
线下零售商进入线上渠道相关文献有Bernstei等[5],他们研究了寡头垄断情况线下零售商进入线上渠道的影响,并指出同时运营双渠道是该市场结构下的必然均衡结果,但不一定能提高利润,可能仅是竞争策略的需要。Yang等[6]指出若线下零售商向双渠道运营转变,影响消费者从线下渠道转移到线上渠道的关键因素是渠道间的协同增强效应和相互减弱效应。Chen Bintong和Chen Jing[7]探究了线下零售商进入线上渠道的条件,指出零售商渠道选择取决于各渠道相对效率的高低。Shao Xiaofeng[8]研究了免运费和按距离计算运费策略对线下零售商进入线上渠道的影响。此外,Brynjolfsson等[9-10]关于线上和线下渠道竞争的实证研究表明,在销售需求量大的主流产品时,存在显著的渠道竞争;但销售需求量小的小众产品时,渠道竞争可忽略不计。
线上零售商进入线下渠道的相关研究较少,Fornari等[11]实证研究了电商是否应当开设实体店的问题,结果表明短期内开设实体店会导致消费者选择线上渠道的概率降低,但在长期会升高;且双渠道的长期协同效应主要来源是区域内实体店的品牌效应。Cao等[12]考虑了线上零售商引入 “线上购买、线下取货”新渠道对需求分配和利润的影响,该新渠道有助于吸引新的客户群体和增加需求,但也会和已有渠道竞争及导致运营成本增加。
产品组合决策的相关研究较丰富,有从产品差异化角度展开的,如Ryzin和Mahajan[13]、Aydn和Hausman[14]考虑了横向差异下的最优产品组合决策问题;Pan和Honhon[15]则研究了纵向差异下的产品组合和价格决策问题。二维差异相关研究有Shao Xiaofeng[16],他研究了消费者有序选择情况下零售商的二维差异产品组合决策问题。基于消费者选择模型角度,多数研究采用multinomial logit(MNL)模型刻画需求,尤其是横向差异产品组合问题的研究,如Ryzin和Mahajan[13]、Cachon等[17]及Aydn和Hausman[14]。Nested multinomial logit(NMNL)模型在研究中也被广泛使用,如Gallego和Topaloglu[18],Feldman和Topaloglu[19]及Li等[20]。
研究多渠道产品组合决策的文献较少,Li等[21]对比了线上和线下渠道销售的区别,综合考虑了线上运输时间和线下库存成本的影响;并指出线上渠道的产品多样化程度不低于线下渠道。Rodríguez和Aydn[22]基于NMNL模型研究了生产商既通过零售商销售也直接向消费者销售产品情况下的产品组合和价格决策问题;结果表明零售商的产品组合是生产商直接向消费者提供的产品组合的子集,且生产商和零售商偏好的产品组合不一致。Dzyabura和 Jagabathula[23]指出对于同时经营双渠道的企业,实体店具有帮助消费者体验产品特性的作用,因此实体店产品组合会影响双渠道的需求,并给出了实体店产品组合决策的近似最优解。申成然等[24]基于网络比价行为研究了双渠道供应链的定价决策及协调策略,并设计了机制使得供应链达到协调。牛志勇等[25]基于公平偏好研究了多渠道零售商是否应当采取线上线下同价策略,结果表明零售商有动机采取同价策略。李佩等[26]指出销售两种替代产品的零售商其双渠道策略总是优于单渠道策略。
综上所述,国内外学者对零售商的全渠道决策和产品组合决策问题进行了大量卓有成效的研究并取得了丰富的研究成果。但部分相关问题研究仍较缺乏。基于零售商全渠道决策角度,多数文献研究线下零售商进入线上渠道的问题,线上电商进入线下渠道的研究不多;多数研究仅考虑零售商销售单产品或有限几种产品的情况,也较少考虑消费者导向类型对渠道决策的影响。基于产品组合决策角度,考虑多渠道产品组合决策的研究较缺乏,且多为渠道间对比或协调,较少考虑零售商渠道和产品组合的联合决策问题。基于上述研究现状,本文的创新有以下几点:第一,基于渠道决策角度,针对两种不同消费者导向类型探讨了电商进入线下渠道的条件,并考虑了电商销售多种产品的情况。第二,基于产品组合决策角度,探讨了电商双渠道运营的产品组合、价格和交付时间的联合决策问题,试图丰富相关理论研究。第三,从现实出发提炼出研究问题,并将渠道决策和产品组合决策相结合,给出了基于两种不同消费者导向类型情况下电商应采取的最优渠道、产品组合、价格和交付时间决策,为现实中企业的运营管理提供一些参考。
2 模型构建
2.1 主要符号
本文采用的主要符号如下:
R:电商R
S:产品组合备选集
Son,Soff:分别为线上和线下渠道产品组合,决策变量
con,coff:分别为线上和线下渠道单位运营成本
k:线下渠道产品组合的基数约束
t:线上渠道交付时间,决策变量
g(t):线上渠道交付成本函数
r:消费者耐心因子,r越大消费者耐心程度越低
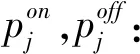
om1,om2:分别为基于产品导向型和渠道导向型消费者的全渠道决策(一般作为下标出现)
γ1,γ2:基于渠道导向型消费者采取全渠道决策时线上和线下渠道的产品异质性程度
Πon:基础模型(仅线上渠道销售)的利润
Πom1,Πom2:分别为基于产品导向型和渠道导向型消费者情况下,电商采取全渠道决策的利润
2.2 问题描述与假设
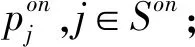
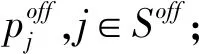
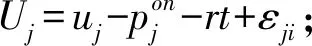
初始情况下R仅在线上渠道销售产品,先决策是否进入线下渠道,然后再决策所选渠道的产品组合、各产品价格及线上渠道交付时间。
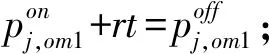
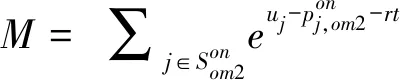

3 基础模型
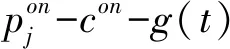
(1)
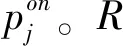
命题1.初始情况R的最优产品组合Son*=S,所有产品的最优价格相同,最优价格和最优交付时间由联立方程组(2)决定。
(2)
若R仅运营线上渠道,因线上渠道不存在空间约束,R可出售全部n种产品来最大限度挖掘市场需求和利润。虽然模型允许对不同的产品区别定价,但结果表明单一定价最优,即使存在定价约束要求同一渠道的所有产品价格相同,结论仍然适用。最优交付时间只与交付成本g(t)的具体形式及消费者耐心因子r有关,消费者耐心程度越低,最优交付时间越短。
将(2)式带入(1)式,得到R的最优利润为:
(3)
(3)式表明,最优利润等于单位产品最优利润减去1,也等于线上渠道的总偏好程度。考虑最优利润和消费者耐心因子之间的关系,可得如下命题。
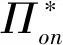
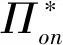
4 基于产品导向型消费者的全渠道决策
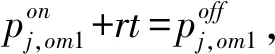
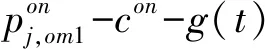
(4)
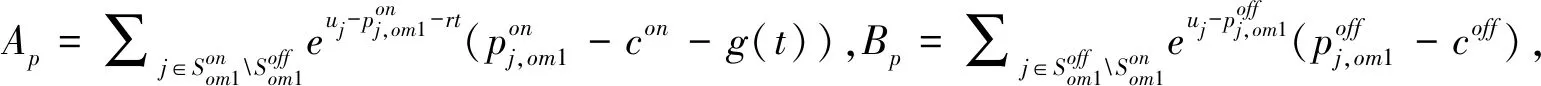
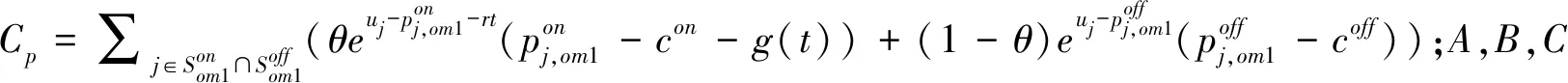
该利润函数较复杂,但能证明R利润最大化时双渠道不存在重复产品,进一步有命题3成立。
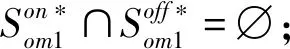
(5)
R利润最大化时双渠道不会出售任何重复产品,因产品导向型消费者能在渠道间自由转换,R无法对不同渠道的同种产品区别定价。一方面,因双渠道运营成本不同,同种产品双渠道同步定价会拉低优势渠道的利润,造成利润损失。另一方面,消费者能在双渠道间自由转换,每种产品仅在单一渠道提供不会损失需求,且因不需要与另一渠道同步定价,反而有更大的定价决策余地和利润空间。
对任意无重复产品的双渠道产品组合, 每个渠道内所有产品具有相同的最优价格,即R只需决策两个价格:线上产品价格和线下产品价格。类似命题1的结论,渠道统一定价的约束并不影响结论,最优交付时间同样仅取决于交付成本函数g(t)的形式和消费者耐心因子r。双渠道单位产品的最优利润相同,否则R可调整双渠道价格来增加利润。
命题3给出了对任意无重复产品的线上和线下产品组合,R决策最优价格及最优交付时间的方法,该决策过程对最优的线上和线下产品组合同样适用。但须先求得最优产品组合,并将最优利润与基础模型对比,以确定R采取全渠道决策是否有利可图,命题4解答了上述问题。
命题4. 当且仅当
(6)
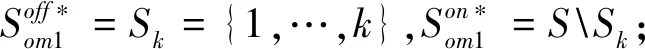

若R进入线下渠道有利可图,线下渠道提供偏好程度最高的k种产品最优。此时线下渠道作为优势渠道,将最受欢迎的产品放在线下渠道销售,能尽可能扩大线下渠道的需求,从而拉高两个渠道的价格和总利润。

将命题4得出的最优线上和线下产品组合代入(5)式可得最优线上和线下价格,再将最优价格带入利润函数(4)可得R的最优利润为:
(7)
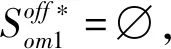
5 基于渠道导向型消费者的全渠道决策
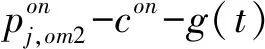
(8)

γ1,γ2分别为线上和线下渠道提供产品的异质性程度,因线上渠道相对线下渠道能提供更多的产品种类数,满足γ1>γ2。Mγ1和Nγ2分别衡量了线上和线下渠道对消费者的吸引程度。将线上渠道产品异质性程度标准化为γ1=1,该标准化并非随意设定,因为若R不进入线下渠道,此时利润函数和基础模型相同;R面对渠道导向型消费者时,初始情况同样可看作全渠道决策的特殊情况。
直接求解最优产品组合存在困难,先从任意的线上和线下产品组合出发,求解此时每种产品的最优价格和线上产品的最优交付时间,有命题5成立。
命题5. 若R基于渠道导向型消费者采取全渠道决策,对任意线上和线下产品组合,各渠道内所有产品的最优价格相同;最优价格和最优交付时间由联立方程组(9)决定。
(9)
最优交付时间仅和交付成本函数及消费者耐心因子有关,且R只需决策线上和线下两个渠道的最优价格,和基于产品导向型消费者采取全渠道决策的结论相同。不同之处在于,因消费者为渠道导向型,双渠道相对独立,因此双渠道的单位产品利润并不相同,由于0<γ2<γ1=1,(9)式表明线下渠道单位产品利润高于线上渠道。这是因为此时渠道间竞争程度低于产品导向型消费者的情况,且进入线下渠道的消费者具有更高的支付意愿,R可在线下渠道设定具有更高单位产品利润的价格。
在此基础上继续求解双渠道最优产品组合,并将最优利润与基础模型对比,分析可得命题6。

若消费者为渠道导向型,R进入线下渠道必然能增加利润,因为此时消费者具有渠道依赖性,双渠道间的竞争程度较低,进入线下渠道能增加消费者的购买方式并满足不同消费者的需求,扩大了总需求进而利润增加。由于双渠道相对独立,因此R可以双渠道出售同种产品,且在线下渠道出售偏好程度最高的产品,线上渠道出售所有产品。这也和现实经验吻合,当某零售商同时经营双渠道时,因线下渠道的空间有限,为最大限度吸引消费者,应提供那些最受欢迎的产品以保证较高的渠道利润,而线上渠道则提供所有的产品以确保较高的总需求。
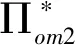
将命题6得出的最优线上和线下产品组合代入(9)式可得最优线上和线下价格,再将最优价格代入利润函数(8)可得R的最优利润为:
(10)
R的最优利润等于线上或线下单位产品最优利润减去各自渠道产品异质性程度的倒数,也等于双渠道的吸引程度除以其产品异质性程度后求和。比较(10)式和(7)式可知,其它条件不变时,基于渠道导向型消费者的全渠道决策其利润高于基于产品导向型消费者的全渠道决策。
6 数值分析
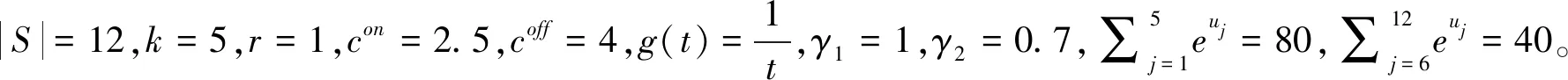
三种情况的最优解如表1所示:
本例满足(6)式条件,因此基于产品导向型消费者,R的最优策略是进入线下渠道销售。表1给出的最优解验证了理论模型的结果,不再赘述。继续考虑参数取值变动对结果的影响,每次仅考虑一个参数的变动,令其它参数固定不变。
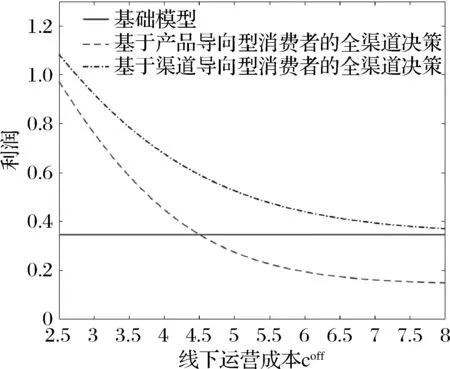
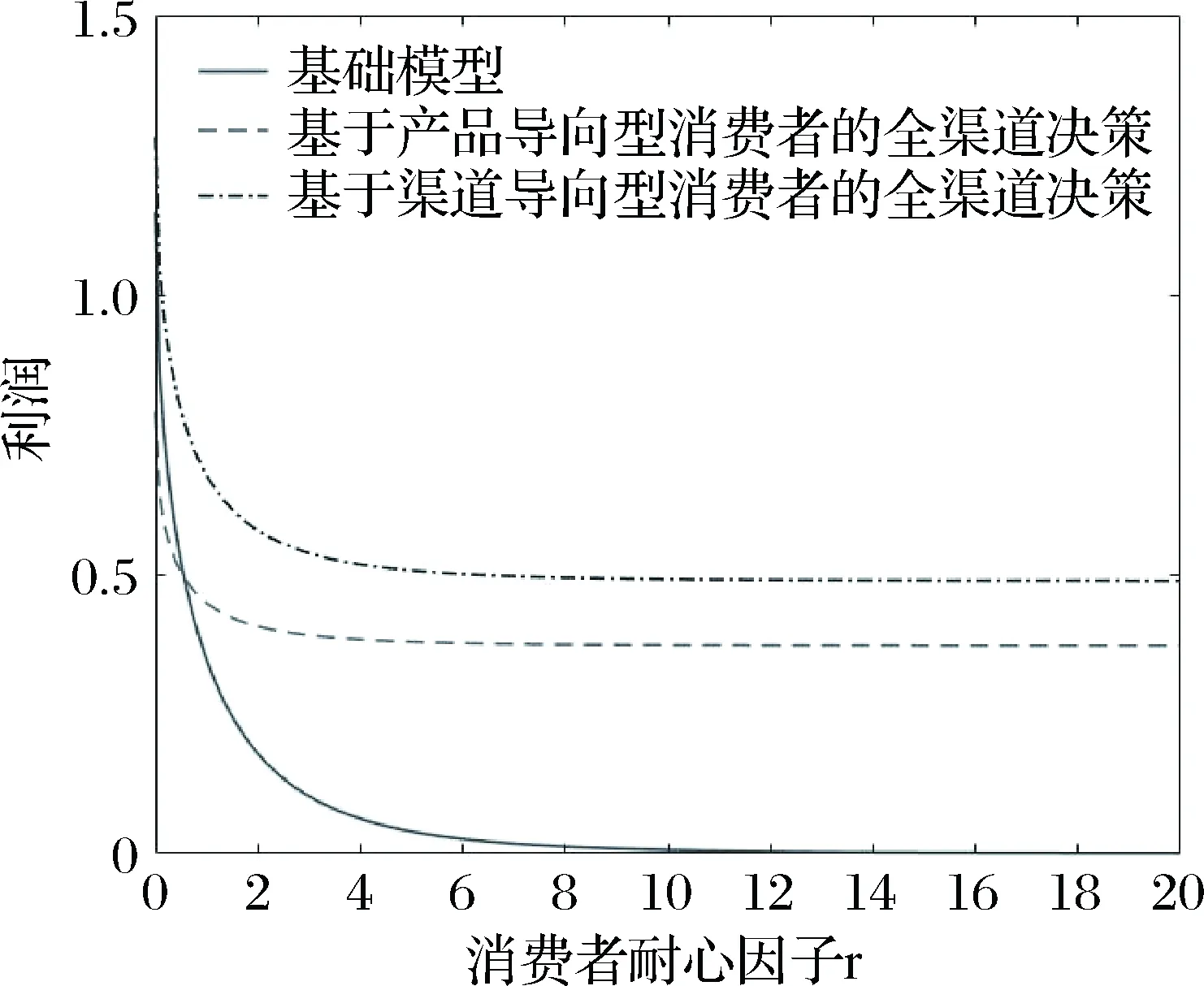
考虑线上运营成本con变化对利润的影响,其余参数取值固定为coff=4,r=1,γ1=1,γ2=0.7;因模型假定con 从图1可知,无论是基础模型还是基于两种消费者导向类型下的全渠道决策,最优利润均随线上运营成本con的增加而下降。若消费者为产品导向型,当con<2时,采取全渠道决策的利润要低于基础模型,只有con>2时,采取全渠道决策才有利可图;若消费者为渠道导向型,全渠道决策的利润始终高于基础模型。基于渠道导向型消费者采取全渠道其利润也高于基于产品导向型消费者的情况。上述结果和理论模型结论相符。此外,随着线上运营成本con的增加,基于两种消费者导向类型的全渠道决策其利润变化幅度相对基础模型更加平缓,因为双渠道运营时通过调整不同渠道价格,R能更有效应对线上运营成本con增加所导致的负面影响。 图1 线上运营成本变化对全渠道利润的影响 研究线下运营成本coff变化对利润的影响,其余参数取值固定为con=2.5,r=1,γ1=1,γ2=0.7;因模型假定coff>con,考虑coff在[2.5,8]范围变动,图2总结了这些结果。 图2 线下运营成本变化对全渠道利润的影响 线下运营成本coff的变化显然不会影响基础模型的利润,R采取全渠道决策的利润随着线下运营成本coff的增加而降低。若消费者为产品导向型,当coff<4.5时(双渠道运营成本之差较小),全渠道决策的利润高于基础模型;当coff>4.5时(双渠道运营成本之差较大),全渠道决策的利润低于基础模型。若消费者为渠道导向型,无论线下运营成本coff如何变化,全渠道决策的利润始终高于基础模型。上述结果验证了理论模型结论。 继续研究消费者耐心因子r变化对利润的影响,其余参数取值固定为con=2.5,coff=4,γ1=1,γ2=0.7;考虑r在[0,20]范围变动,可得图3的结果。 图3 消费者耐心因子对利润的影响 消费者耐心因子r的增加意味着消费者耐心程度降低,从而最优交付时间减少且最优交付成本增加,这将导致线上价格的提高进而导致利润降低,这验证了理论模型的结论。需注意随着r的增加,基础模型的利润变得很低,如消费者耐心因子r>10,基础模型的利润接近零。但是若R采取了全渠道决策,无论基于哪种消费者导向类型,随着消费者耐心因子r的增加,利润不会趋于零。因为消费者耐心因子r很高意味着线上渠道的利润空间很小,仅运营线上渠道所获取的利润很低;但是若R进入了线下渠道,则可从线下渠道获取相对较高的利润。这表明在消费者耐心程度较低时,R有必要采取全渠道决策,此时线下渠道为主要利润来源。 最后研究R基于渠道导向型消费者采取全渠道决策时,线下渠道产品异质性γ2对利润的影响。其余参数取值固定为con=2.5,coff=4,r=1,γ1=1;因模型中假定γ2<γ1=1,考虑γ2在[0.2,1]范围变动,结果如图4所示。 随着线下产品异质性程度γ2的上升,R基于渠道导向型消费者采取全渠道决策的利润降低。这是因为当线下产品异质性程度较低,渠道间竞争程度较低,线下渠道的单位产品利润也较高,从而拉高了线上渠道产品的价格和单位利润。但随着线下渠道产品异质性程度的增加,线下渠道和线上渠道之间的竞争更加激烈,因此会导致线上和线下价格均降低,进而导致利润降低。 本文从现实情景出发,基于不同消费者导向类型研究了电商的全渠道决策问题。首先建立基础模型研究了电商单渠道销售的初始情况,并得出最优产品组合、价格和交付时间;在此基础上考虑两种不同的消费者导向类型:产品导向型和渠道导向型。分别基于上述两种消费者导向类型,研究电商进入线下渠道的条件,及全渠道决策情况下应当如何决策双渠道的产品组合、价格及交付时间。具体研究结论如下:第一,最优交付时间只和消费者耐心程度及交付成本函数的形式有关;且消费者耐心程度越高,则最优交付时间越长,电商利润也越高。每个渠道内所有产品的最优价格相同,即只存在渠道间的区别定价,不存在渠道内的区别定价。上述结论对基础模型和基于两种不同消费者导向类型的全渠道决策均成立。第二,若消费者为产品导向型,仅当双渠道运营成本之差较小且消费者耐心程度较低时,电商进入线下渠道有利可图。若进入线下渠道有利可图,最优产品组合是在线下渠道提供最受欢迎的产品,在线上渠道提供剩余产品,且需保持双渠道单位产品利润相等。第三,若消费者为渠道导向型,电商进入线下渠道必然有利可图,且最优产品组合是在线下渠道提供最受欢迎的产品,在线上渠道提供所有产品,且线下渠道单位产品利润更高。此时的双渠道价格和单位产品利润均高于电商基于产品导向型消费者采取全渠道决策的结果。 基于理论结果,得到如下几点管理启示:第一,电商在做出全渠道决策时需综合考虑消费者类型、线上线下运营成本差异和消费者耐心程度的影响。若消费者为产品导向型,可通过管理和技术手段降低线下运营成本,为进入线下渠道创造充分条件,进而扩大需求和利润。若消费者为渠道导向型,应当尽快进入线下渠道抢占资源。第二,若电商已进入线下渠道,因双渠道运营不可避免带来渠道竞争,基于不同消费者导向类型应采取不同的产品组合和定价策略,尽可能减少其负面影响。若消费者为产品导向型,应当确保每种产品仅在单一渠道提供,且保持双渠道单位产品利润相同。若消费者为渠道导向型,应当在双渠道同时出售最受欢迎的产品,且通过价格歧视保持线下渠道单位产品利润更高。第三,若消费者耐心程度很低,表明线上渠道利润空间较小,电商一方面需进入线下渠道并将线下渠道作为主要利润来源,另一方面可通过管理和技术手段,降低交付成本和交付时间,进而提高线上渠道的需求和利润。 附录 命题1证明:首先用反证法证明Son*=S。假设Son*⊆S,考虑在Son*中添加SSon*中的所有产品,显然若有: (A.1) 则可得: (A.2) R的利润函数可写成: (A.3) 连续可微的有界函数,其最大值只可能在边界和驻点取得,若边界无法取得最大值且定义域内驻点唯一,则最大值必然在唯一的驻点取得。首先证明利润函数的满足上述性质。 (1) Πon有界且连续可微 (2)最大值点在驻点取得 (A.4) 因产品l的选择是任意的,可以断定所有产品的最优价格相等,用pon*表示,可得: pon*-con-g(t*)-1=∑j∈Seuj-pon*-rt* (A.5) g′(t*)=-r (A.6) (A.5)和(A.6)联立即为(2)式,还需考虑驻点的唯一性及是否在定义域范围内,显然t*>0且唯一,(A.5)左边随pon*的增加而增加,右边随pon*的增加而减少,因此pon*唯一。因等式右边为正值,则pon*>0,即驻点有意义且唯一,证毕。 (A.7) 证毕。 (A.8) 由利润函数(4)分子中的 (A.9) R的利润函数简化为: (A.10) A,B,Ap,Bp的具体表达式正文已给出。 显然Πom1有界连续可微且最大值在驻点取得,证明过程类似命题1,不再赘述。 (A.11) (A.12) (A.13) g′(t*)=-r (A.14) con-coff+g(t*)>-rt* (A.15) (A.16) 证毕。 命题5证明:首先需证明Πom2有界连续可微,且最大值在驻点取得。证明过程与命题1类似,故省略。 (A.17) (A.18) g′(t*)=-r (A.19) 命题6证明:因对于任何线上和线下产品组合,利润最大化条件下各渠道内的产品价格相同,因此利润函数可以写为: (A.20) (A.21) (A.22) 证毕。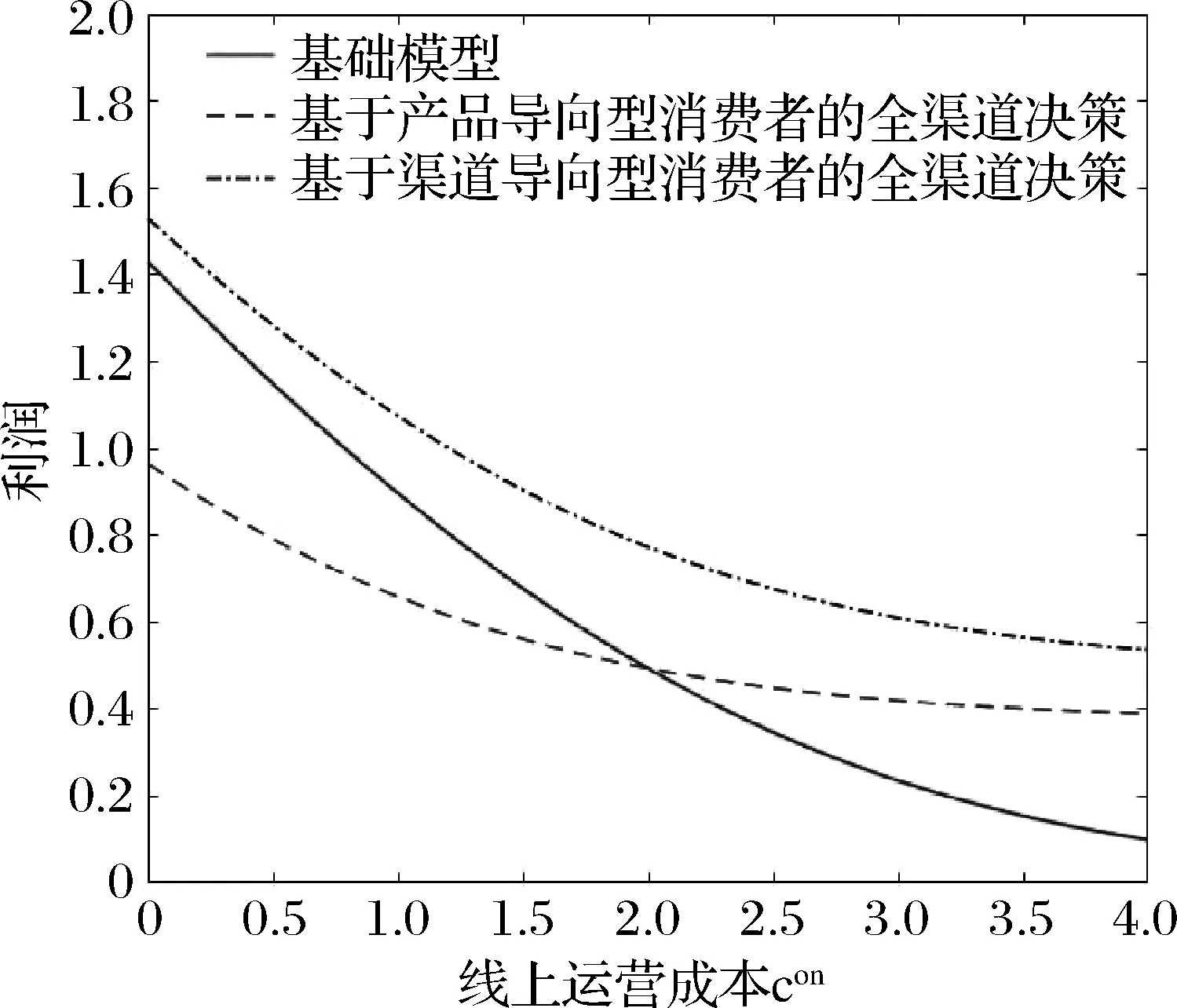
7 结语