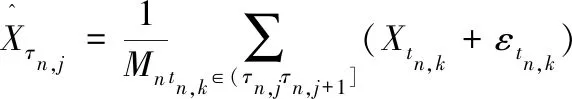带有市场交易信息和随机微观噪声下的杠杆效应研究
苑慧玲,徐 路, 周 勇
(1.香港城市大学数据科学学院,香港 999077;2. 申万宏源证券有限公司博士后科研工作站, 上海 200031;3. 复旦大学理论经济学博士后流动站, 上海 200433;4. 统计与数据科学前沿理论及应用教育部重点实验室,华东师范大学统计交叉科学研究院和统计学院, 上海 200062)
1 引言
杠杆效应一直是金融市场上研究的热点问题,它是对波动率非对称性的一种解释,描述的是资产波动率和收益率之间的一种负相关关系。Black[1]和Christie[2]首次给出了杠杆效应的解释:当资产价格下降的时候,公司的杠杆(债券比)变大,引起股票的波动率大幅度变化,从而造成更大的风险。随后,大批学者和金融学家投入到对杠杆效应及波动率非对称性的研究中。Nelson[3]提出ARCH模型的一种新的形式,解决了经典的ARCH 模型和GARCH 模型不能解释非对称性现象的缺陷。基于波动率非对称性现象,Engle和Ng[4]提出了EGARCH模型。Bekaert和Wu[5]通过比较杠杆效应和其它用于描述波动率非对称性的解释,从公司层面提出了协方差非对称性。Bouchaud等[6]提出了收益率和波动率之间的瞬时相关关系。Bollerslev等[7]利用高频数据进行实证分析发现,过去和现在的收益率与现在的收益率的绝对值之间存在较强的负相关关系,而现在的波动率和滞后的收益率之间存在较弱的负相关关系。也有相当多的学者对杠杆效应的估计进行了研究。最近,Ait-Sahalia等[8]考虑如下的杠杆效应(瞬时杠杆效应)
其中Xt和σt表示资产在时刻t的真实价格和其市场波动率。通常由于市场微观噪声的存在,资产市场价格Xt无法直接观察到,因此,无法应用通常的办法对杠杆效应ρt估计,甚至无法估计市场波动率σt。为此,Ait-Sahalia等[8]考虑了如下加性微观噪音模型,
Yt=Xt+εt
其中Xt和Yt分别表示资产在时刻t的真实价格和市场价格,εt是白噪声。模型表明真实的资产价格无法直接可观察,而观察到的市场资产价格受到噪音交易的影响。Ait-Sahalia等[8]利用收益率和波动率估计(例如:TSRV (Zhang等[9]) 和PAV (Jacod等[10])) 之间的相关系数对杠杆效应ρt进行了估计,基于加性微观噪声模型,他们提出的杠杆效应估计具有优良的统计性质,然而此类杠杆效应估计由于估计偏差和噪声误差的存在,引起了杠杆效应之谜。
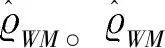
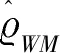
早在二十世纪八十年代,就有关于市场微观噪声结构的研究。Roll[13]提出微观噪声受市场买卖价差的影响。
εt=αIb/s(tk).
其中,Ib/s(tk)表示在时刻tk的交易类型,如果是交易买方,Ib/s(tk)=1,如果是交易卖方,Ib/s(tk)=-1。Gloste和Harris[14]扩展了Roll的模型,指出市场微观噪声除了受交易类型的影响,也受交易量的影响,Harris[15]发现影响微观噪声的因素有很多,除了交易类型和交易量还具有其他因素。Almgren和Chriss[16]提出了市场微观噪声受交易量和交易率的影响,并建立了模型
εt=αIb/s(tk)+βIb/s(tk)Vtk/Δtk.
其中Vtk表示在tk的交易量,Δtk=tk-tk-1表示两笔交易的时间差,Vtk/Δtk表示交易率。
由此表明市场微观噪声结构是复杂的,在我们分析高频金融市场时候,应当充分考虑市场微观噪声结构。LI Yingying等[17]在研究可积波动率的时候首先将市场微观噪声的交易信息用一个参数函数g(Ztk,θ)表示:
Ytk=Xtk+g(Ztk;θ0),0=t0t1…tn=1,
(1.1)
其中Ytk是在时刻tk观测的log价格,Xtk表示真实的log价格,Ztk是信息集,包含但不尽然是交易量,交易类型和买卖差弹性,θ0是有限维的参数,以及g(Ztk,θ0)是Ztk和θ0的任意参数函数形式。
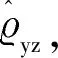
高频金融市场的微观噪声结构应该蕴含丰富的信息,模型(1.1)并不是充分的。Li Yingying等[17]拓展了模型(1.1),提出了下面的模型结构。
Ytk=Xtk+g(Ztk;θ0)+εtk,
0=t0t1…tn=1
(1.2)
其中,Ytk,Xtk和g(Ztk,θ0)与模型(1.1)里的符号表示相同的含义,εtk是独立同分布的,均值为0,标准差为a,且独立于F1。由此看出,模型(1.2)中加入了随机微观噪声变量,比模型(1.1)具有更广泛的实际意义。本文旨在基于模型(1.2)提出新的杠杆效应估计,研究新估计的统计性质,并且探讨此估计的应用价值。
本文的结构安排如下:2.1部分重述杠杆效应产生的随机模型机制,2.2部分在较为广泛的模型(1.2)下提出杠杆效应估计,2.3部分研究提出的杠杆效应估计的统计性质,给出杠杆效应估计的3个定理;有关杠杆效应估计的模拟分析在第3部分;杠杆效应的实证分析在第4部分;结语在第5部分;所有证明在附录部分。
2 杠杆效应估计方法及其统计性质
2.1 随机模型机制
在金融市场上,最流行的随机过程是过程:
dXt=μtdt+σtdWt,X0=x0,
(1)
其中,Wt是一个维纳过程,μt和σt是适应的局部有界的随机过程, 并且,Wt,μt和σt都是定义在概率空间(Ω,F,P)上的。
可积波动率可以定义为:
(2)
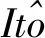
dσt=atdt+btdWt+gtdBt
(3)
其中,Bt独立于Wt的维纳过程, at,bt,gt和σt都是局部有界的。
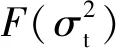
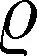
(4)
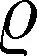
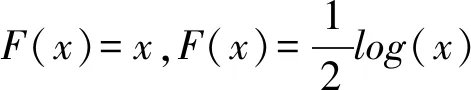
2.2 杠杆效应估计方法的提出
针对随机过程Xt,考察n个等分时间区间,令0=tn,0tn,1tn,2…,tn,n=T,那么时间间隔不失一般性,令T=1。首先,基于微观噪声结构模型(1.2),我们可以得到观测价格Xtn,k+εtn,k的估计为其次,把n个价格观测值重新化分为n′个区间,每个区间长度是区间个数具体区间为H=0=τn,0τn,1τn,2…,τn,n′-1=T,在划分的区间[τn,j,τn,j+1],可以得到真实价格Xτn,j的估计为的样本均值。即:
(5)
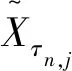
于是,在模型(1.2)下,杠杆效应估计可以定义为:
(6)
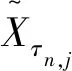
(7)
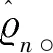
2.3 杠杆效应估计的统计性质
下面给出一些假设:
假设2
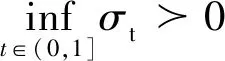
(ii) 对所有的k,在Ftk-1的条件下,Ztk和ΔXtk都是条件独立的;
假设3
(ii) 当θ∈N(θ0)时,g(Z;θ)以及g(Z;θ)关于θ的一阶,二阶导数是局部有界的;
(iii) 对任意的ε>0,当n→∞时,
几乎处处成立;
(iv)

注释1
假设2是连续随机模型和回归模型的常见假设,假设3中的(i)-(iii)是关于计算极大似然函数估计的假设,假设3中的(iv)是Fisher信息阵可逆性的假设。
定理1
(A1). 当假设1-3成立,T固定的时候,
(8)
(9)
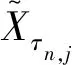
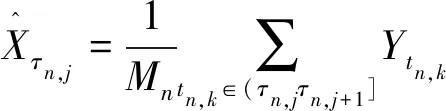
的表述可见Wang和Mykland[11]的4.1部分。
(A2). 当假设1-3成立,T固定的时候,
+op(n-1/2)
(10)
其中:
为Wang 和Mykland[11]在考察市场微观噪声为白噪声的情形下提出的杠杆效应估计。
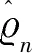
定理2
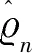
(11)
其中Z是一个标准的正态的随机变量,并且独立于FT,bt,gt,at和μt都是局部有界的。
注释2

令Zn为一系列χ-测度的变量,F1⊂χ。当n→∞时,我们称Zn以F1-稳态收敛到Z,假如Z是χ的一个扩展,A∈F1,对于任意有界的连续函数g(·)当时,
E(IAg(Zn))→E(IAg(Z))。
(2)通过最小化定理2中的渐近方差,可以得到c和c1的最优值:
(12)
和
(13)
其中,
实际上,c和c1的值可以由最小化方差的渐近形式得出。令
和
通过简单的计算(见附录),我们可以获得下面的等式成立:
以及:
容易看出:
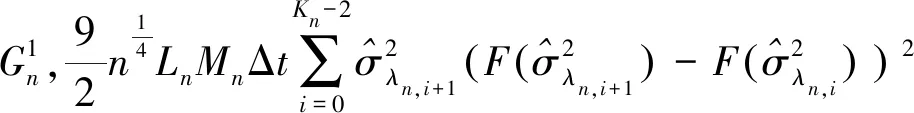
定理3
当假设1-3成立,T固定,并且的时候,
其中Z1是标准的正态随机变量,且独立于域流FT。
3 模拟分析
对于隐含的log价格Xt,Heston模型如下:
(14)
(15)
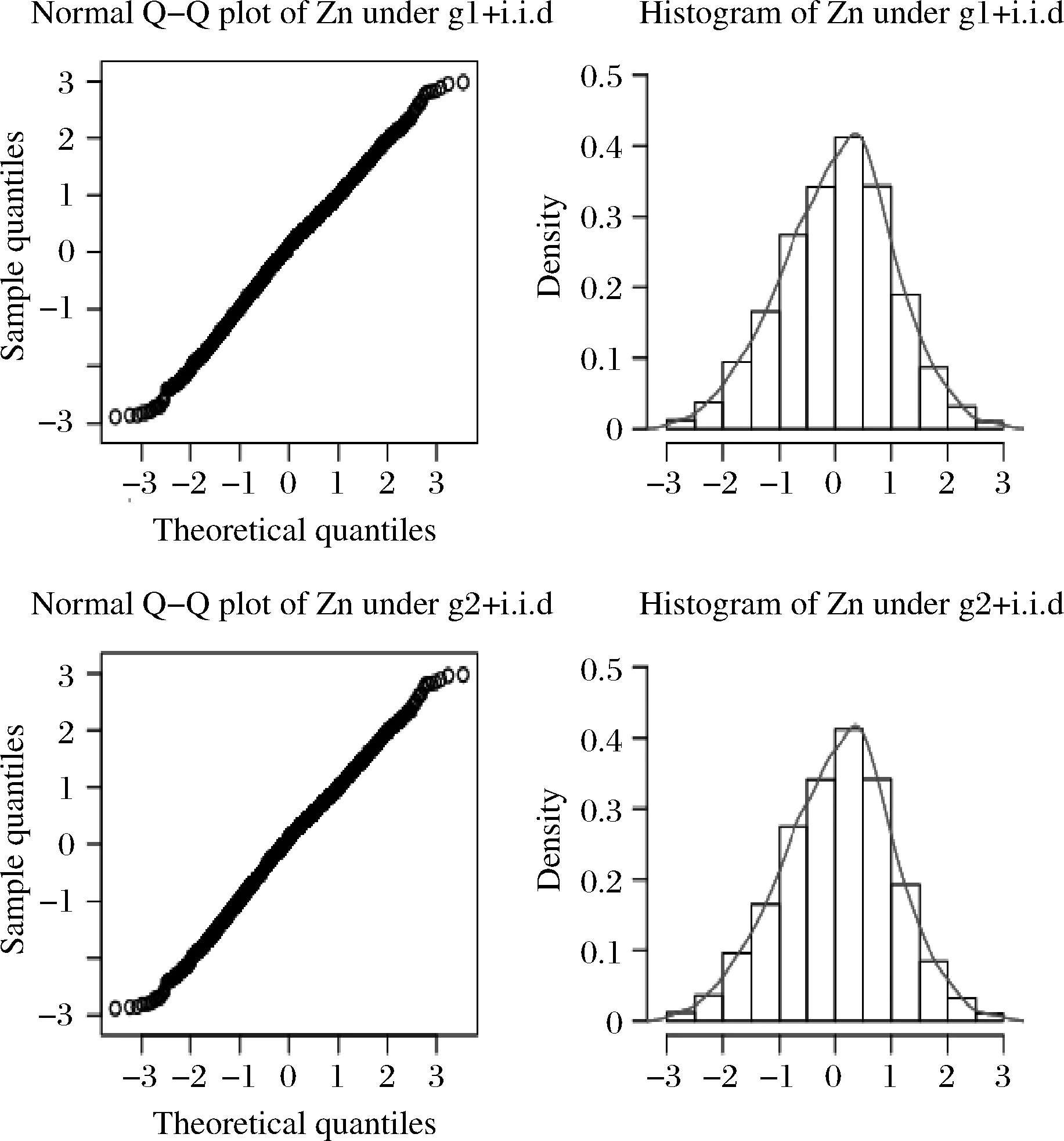
我们选取两个包含交易信息的高频金融市场微观噪声模型g1(Vtk,Ib/s(tk);α,β)和g2(Vtk,Ib/s(tk);β,ζ)。g1(Vtk,Ib/s(tk);α,β)是Almgren和Chriss[16]提出的市场微观噪声关于交易量和交易率的线性模型。g2(Vtk,Ib/s(tk);β,ζ)是Keim和Madhavan[19]提出的市场微观噪声模型关于交易信息的非线性模型。而
g1(Vtk,Ib/s(tk);α,β)=αIb/s(tk)+βIb/s(tk)Vtk/Δtk
g2(Vtk,Ib/s(tk);β,ζ)=Ib/s(tk)log(ζ+βVtk/Δtk)
其中,Ib/s(tk),Vtk和Vtk/Δtk与Almgren和Chriss[16]文中表示相同,比较g1(Vtk,Ib/s(tk);α,β)和g2(Vtk,Ib/s(tk);β,ζ),当交易量低的时候,它们是非常接近的。
g1(Vtk,Ib/s(tk);α,β)+εtk,
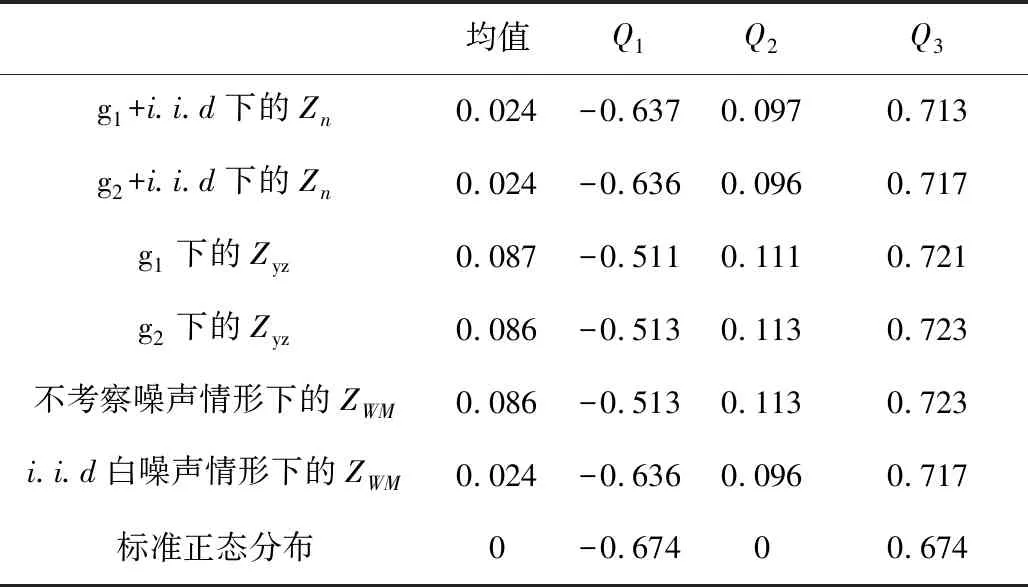
0=t0 (16) g2(Vtk,Ib/s(tk);β,ζ)+εtk, 0=t0 (17) (18) 为了便于计算,选取F(x)=x,T=1。 图1 在市场微观噪声模型g1(·)和白噪声及其g2(·)和白噪声下Zn的Q-Q图和直方图 表1 比较Zn,Zyz,ZWM的均值, Q1,Q2,Q3 表2 比较下的方差, 偏差, 均方误差 众所周知,沪深300指数是由上海和深圳证券市场中市值大、流动性好的300只A股作为样本编制而成的成份股指数,具有良好的市场代表性。沪深300指数是沪深证券交易所第一次联合发布的反映A股市场整体走势的指数。它的推出,丰富了市场现有的指数体系,增加了一项用于观察市场走势的指标,有利于投资者全面把握市场运行状况,也进一步为指数投资产品的创新和发展提供了基础条件。在金融市场上,金融产品的未来波动率估测非常重要,可惜的是我们无法给出未来波动率的估计,但是通过收益率与波动率之间的关系可以提供预测波动率的一种思路。为此,研究以沪深300指数作为标的物的沪深300股指期货的杠杆效应对波动率预测的影响将对相关金融部门进行金融指导具有深远的意义。 一般来讲,中国市场上的期货交易时间是每周一至周五的上午9:30-11:30和下午1:00-3:00。然而,大量实证研究表明期货在开盘和闭盘时会出现大量交易,波动率呈现大幅度变化。为了避免股票市场上出现此种情况下不稳定的交易活动,我们删除股票开盘和闭盘前五分钟的交易数据,分析每个交易日时间区间在上午9:36至下午2:55的高频数据,那么研究的每个交易日的数据个数为230。此外,为了便于分析,如果某个交易数据出现删失数据,我们将删除这个交易日的所有数据。清洗数据后,到期时间为2018年9月21日的期货合约高频数据个数为36110(157个交易日);到期时间为2018年12月21日的期货合约高频数据个数为36340(158个交易日)。 所有高频数据中的期权合约价格应当转化为log价格,同时为了便于分析,log股票价格乘以100为100×log(Pn,d),n=1,…,N,d=1,…,230,其中Pn,d在第n个交易日,第d个1分钟的期货合约价格。 波动率预测一直是金融市场上研究的热点。有大量模型用于预测波动率,例如:经典的长记忆ARFIMA模型,GARCH模型和随机波动率(SV)模型(参见Koopman等[20])。国内学者也对波动率的预测模型进行了研究,刘晓倩等[21]基于高频金融数据提出了HAR-CVX模型,并对沪深300指数的波动率预测进行了分析,发现此时的模型具有更好的预测效果。沈根祥等[22]将提出的已实现GAS-HEAVY模型,应用到沪综指、深成指和沪深300指数的波动率预测研究中,分析得出已实现GAS-HEAVY模型可以做为金融市场上波动率预测的计量工具。本节旨在分析杠杆效应对波动率预测是否有显著的作用,不着重分析波动率预测模型的选取,为此我们选择了简单的波动率模型。 (19) 5) ΔXti=Xti-Xti-1和i都是高斯过程; 利用公式(19)考察杠杆效应在波动率预测中的作用。所有结果可见表3-表6。注意表中“***”表示在0.001的置信水平下参数是显著的,“**”表示在置信水平0.01下参数是显著的,“*”表示在0.05置信水平下参数是显著的,和“·”表示在置信水平0.1下参数是显著的。 表3 在(3.3)下, 沪深300股指期货的波动率预测结果(2018.1.22-2018.9.21) 在表3和表4中,杠杆效应α4的P值分别是0和0.042,说明合约时间为2018年1月22日到2018年9月21日沪深300股指期货的杠杆效应在对未来一天波动率的预测具有显著性的影响。相对而言,表3和表4中的隔夜收益率的P值都大于0.1,表明隔夜收益率对未来一天波动率的预测没有显著性影响。但是,前一天波动率的变化对未来一天波动率是有显著性影响的,前两天波动率的变化在交易信息为线性模型下,对未来一天的波动率预测具有较为显著性的作用。 表4 在(3.4)下,沪深300股指期货的波动率预测结果(2018.1.22-2018.9.21) 比较表5和表6,在市场微观噪声模型(16)和(17)下,隔夜收益率α3的P值都是大于0.1 的,表明隔夜收益率对未来一天的波动率预测没有显著性影响。杠杆效应α4在模型(16) 下的P 值等于0.000,而在模型(17)下的P值大于0.05,但是小于0.1,说明杠杆效应在交易信息的线性噪声模型下,对未来一天的波动率具有显著性影响,而在交易信息的非线性噪声模型下,对未来一天的波动率具有较小影响。事实上,在噪声模型(17)下,选取的波动率预测模型(19)的调整后的R2=0.322,说明模型(19)并不是很好的,但是,由于杠杆效应在交易信息的线性噪声模型下,对未来一天的波动率具有显著性影响,所以基于波动率预测模型(19),在某种程度上表明杠杆效应对未来一日波动率是具有显著性作用的。但是,前一天波动率的变化和前两天波动率的变化对未来一天波动率是有显著性影响的。 表5 在(3.3)下, 沪深300股指期货的波动率预测结果(2018.4.23-2018.12.21) 表6 在(3.4)下,沪深300股指期货的波动率预测结果(2018.4.23-2018.12.21) 附录: 定理1的证明 首先证明定理1(A1),其次证明定理1(A2)。由于本文是在模型(1.2)下研究的杠杆效应估计,所以通过模型(1.2)和(5),可以得出 由于 =:I1+I2+I3+I4+I5+I6. 所以 和 此外, 上式成立是由于假设2(ii)和白噪声εtn,k。上式的右边其实是Mn个具有相同界的和,于是上式可以写作: (1.3) 并且定义关于任意函数φ:N(θ0)→,对任意的h≻0,有: ω(φ,h):=sup{|φ(θ1)-φ(θ2)|∶|θ1-θ2|≤h}, 则对任意θ1,θ2∈N(θ0)和≤N,存在C使 E|Fn(θ1)-Fn(θ2)|≤C|φ(θ1)-φ(θ2)|, 上面不等式的成立是由于假设3(ii)以及Li Yingying[17]文中的定理3。 利用Kallenberg[23]中的推论14.9中的证明,对任意≻p/2和m∈,我们可以获得: E(ω(Fn,2-m))≤C2-m(2-p) 选取满足2-m≥K/n≻2-m-1,有: E(ω(Fn,K/n))≤C(K/n)=O(n) 因此对所有n,B(θ0,K/n)=({θ:|θ-θ0|}≤K/n)⊆N(θ0),而对所有≻p E(ω(Fn,K/n))=Op(n), 从而对任意K≻0,(1.3)式等于op(n-1/2),定理A1中(9)式得证。 下面证明定理1中的(A2)。 =:I7+I8+I9. |F′(·)|≤M 故 |I8+I9| 最后一个等式成立是由于Kn=Op(n1/4),而且Xλn,i+1满足公式(1),是局部有界的,则: |I8+I9|≤6M·op(n-1/2) 因此, 所以定理1(A2)得证。 定理2的证明 定理3的证明 通过简单计算,容易可得定理3成立。
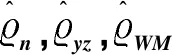
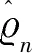
4 实证分析
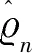
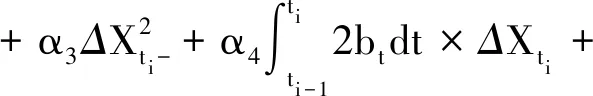
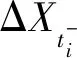
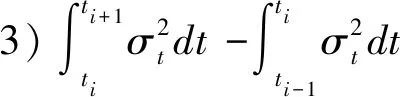
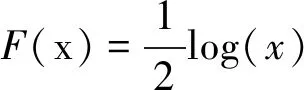
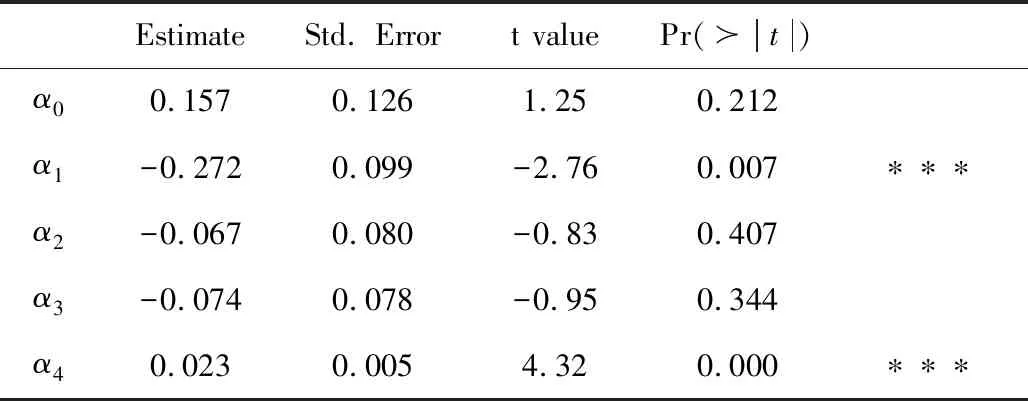
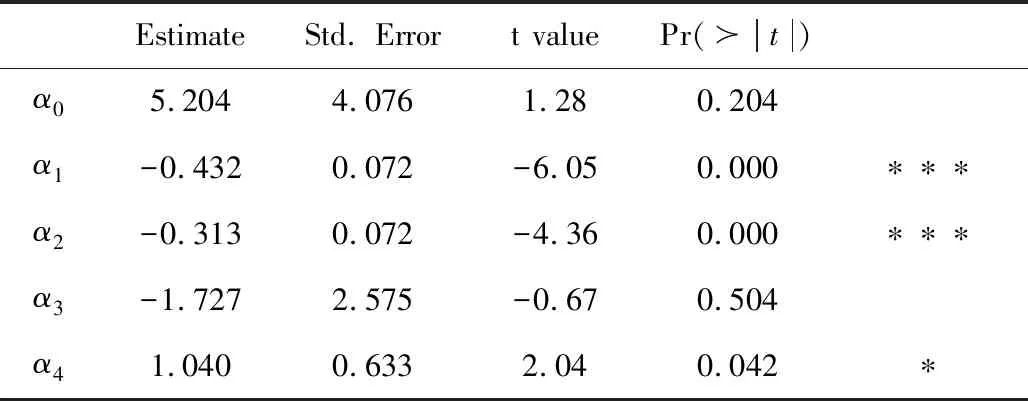
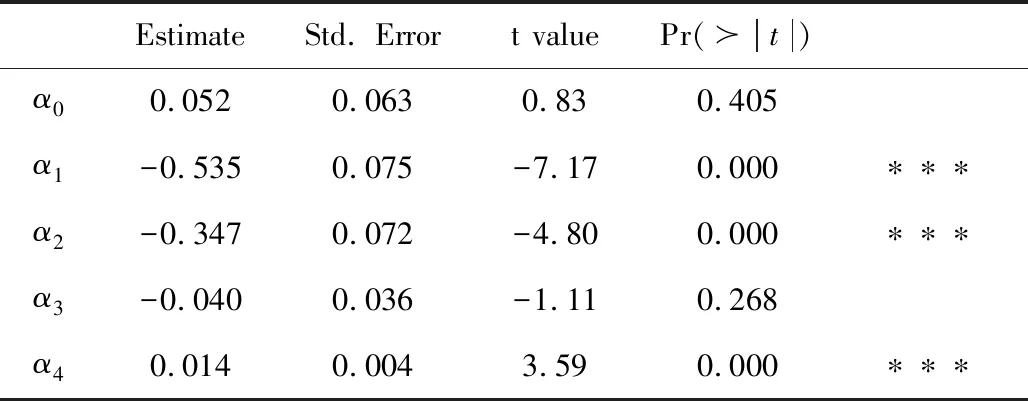
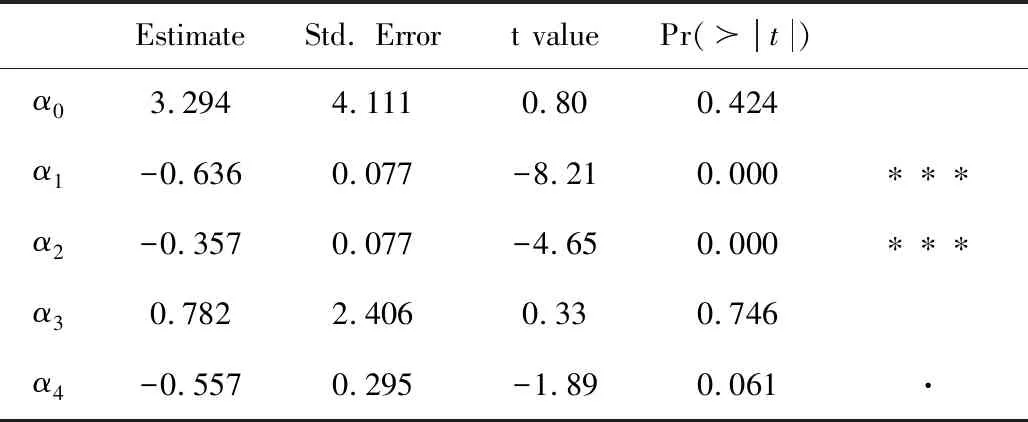
5 结语