变质心高超声速再入飞行器建模与特性分析

樊博璇 陈桂明 林洪涛

变质心高超声速再入飞行器建模与特性分析

樊博璇1陈桂明1林洪涛2

（1. 火箭军工程大学，西安 710025；2. 中国人民解放军31004部队，北京 100091）

建立了一维变质心滚控高超声速再入飞行器的完整动力学模型。对变质心飞行器弹道及姿态动力学进行研究，明确了变质心滚控飞行器的控制机理与特点，同时针对其通道间的耦合效应以及执行机构参数设置对控制能力的影响分析，提出了飞行器结构设计和控制系统设计的相关要求，为高超声速再入飞行器的工程实践提供理论基础。

高超声速再入飞行器；变质心控制；动力学

1 引言

变质心技术是机动变轨突防的一种新形式，相比其他传统控制技术（如空气舵控制、发动机控制等）具有低成本、高效率等优势，可有效提高高速飞行器的突防能力[1～3]。

美国是最早开展再入飞行器变质心控制研究的国家之一[4～6]。1997年，俄罗斯研制的白杨M导弹也采用变质心控制技术成功实现了弹道修正[7]。国外对变质心控制已有较为深入的研究，并进入工程实践阶段。国内对变质心控制技术的研究起步较晚，西北工业大学是较早涉及这方面研究的单位，易彦等[8]利用拉格朗日法对变质心旋转飞行器建立了六自由度动力学方程，并对活动质量体的运动所带来的姿态角变化进行了仿真。周军等[9]研究了三维变质心非交互控制的可解性问题，给出三种变质心非交互控制实现性类别及分类判断方法。陈升泽等[10]采用反演设计方法，引入虚拟控制量，设计了一种针对双活动质量块变质心飞行器的滑模变结构姿态控制器。高长生[11]利用 Newton-Euler 法建立了携带三个活动质量体的飞行器动力学模型，并在滚动稳定作为约束条件下对俯仰-偏航通道动力学进行了分析。刘智陶等[12]针对单质量块滚控式变质心飞行器的欠驱动问题，设计了一种自抗扰控制器进行滚偏耦合控制。目前国内关于变质心控制技术仍处于理论研究阶段，主要集中于多质量块的配平控制分析及控制器设计，而对一维单质量块滚控式变质心飞行器的机理分析、控制性能问题的研究较少，对于高超声速再入飞行器变质心控制的完整建模和系统分析缺乏系统研究。

本文以一维变质心滚控高超声速再入飞行器为研究对象，基于牛顿力学建立了包含质量块运动模型的完整动力学模型；然后通过理论分析与仿真，研究变质心高超声速再入飞行器的飞行路径及姿态动力学，明确变质心控制机理与特点；最后结合飞行器质心运动方程，分析了各方案下飞行器机动能力及变质心机构控制能力，为高超声速再入飞行器变质心控制机理的分析与制导控制系统的设计提供一定的理论基础。

2 飞行器动力学建模

本文研究对象如图1所示，整个飞行器系统主要包括飞行器壳体和一套变质心机构，变质心机构由可移动质量块（实线部分）和不可移动部分（虚线部分）组成，O为飞行器壳体质心，O为可移动质量块质心。飞行器采用固定配平攻角外形，通过单轴滑动飞行器内部质量块形成的气动力矩调节飞行器姿态角，使飞行器按一定的弹道轨迹运动。

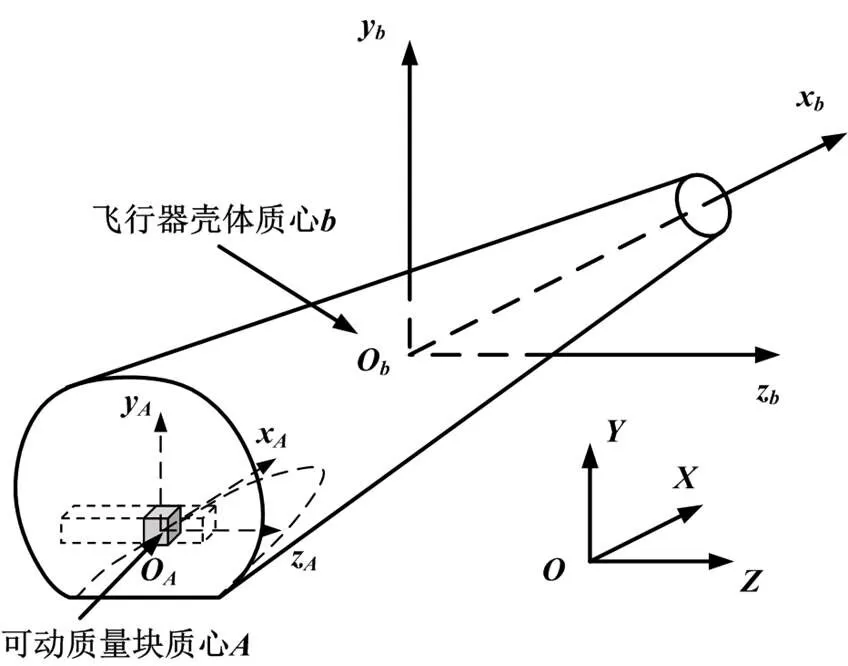
图1 一维变质心滚控飞行器示意图

飞行器建模时所用的坐标系及符号定义如下：

在建立一维变质心再入飞行器动力学模型时，只考虑再入段飞行器质点系所受的重力、空气动力和空气动力矩。

2.1 壳体质心平动动力学方程

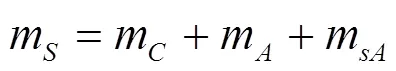
在惯性系下，飞行器各部分质心矢径和飞行器系统总质心矢径有关系式：

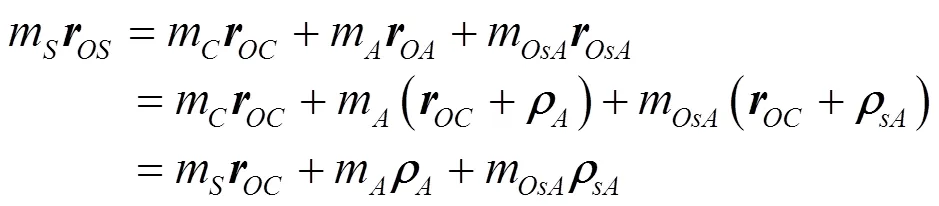
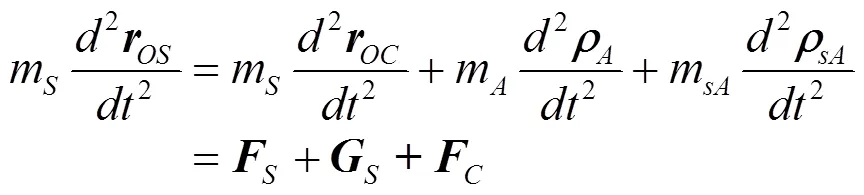
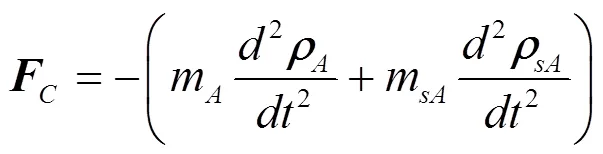
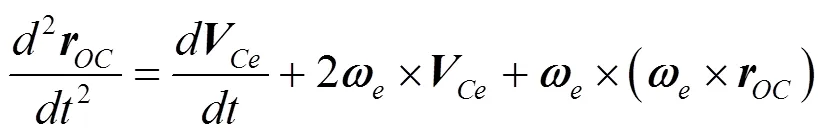
则式（3）可改写为：

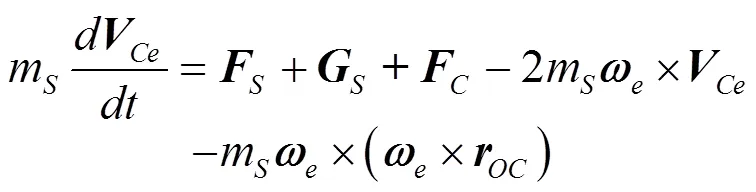
式（6）在弹道系中表示为：

a. 相对加速度

式（7）等号左边可表示为：

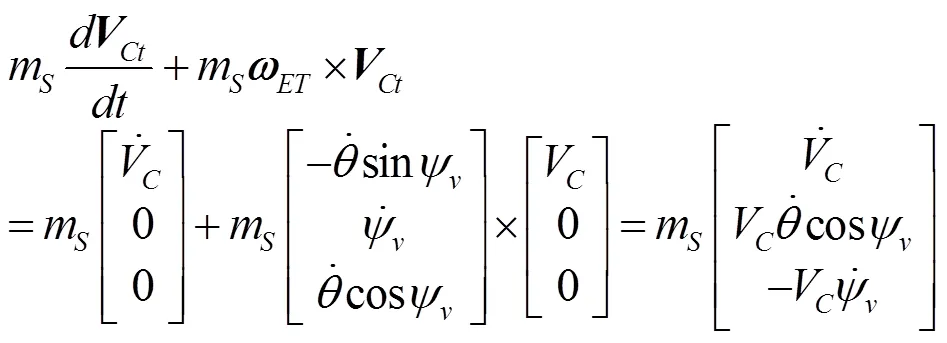
b. 地球引力

再入系中，根据式（4），弹道系下的地球引力可表达为：

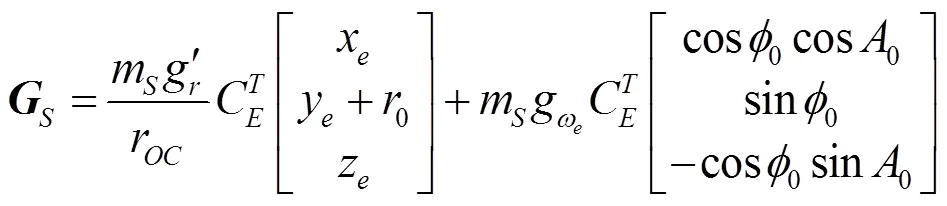
c. 空气动力

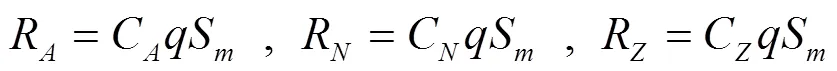
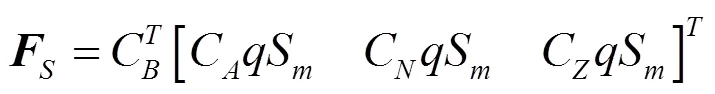
d. 牵连加速度

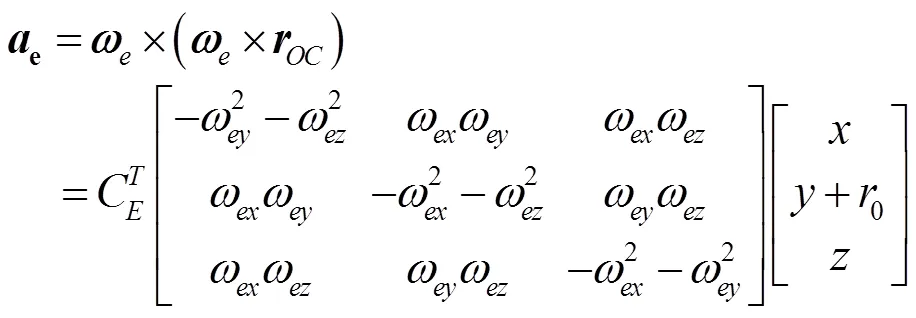
e. 哥氏加速度

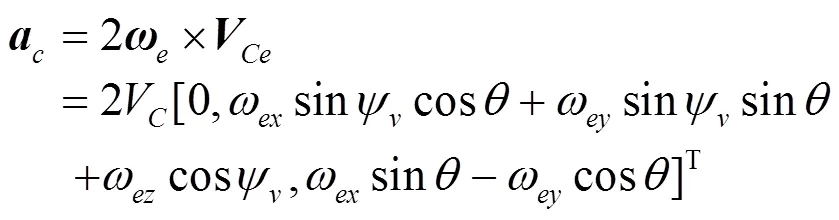
f. 变质心机构引起的附加惯性力

将以上各项代入式（7），可得到弹道系下一维变质心飞行器的质心动力学方程：

2.2 绕壳体质心转动动力学方程

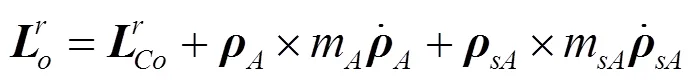
根据相对动量矩定理可得：

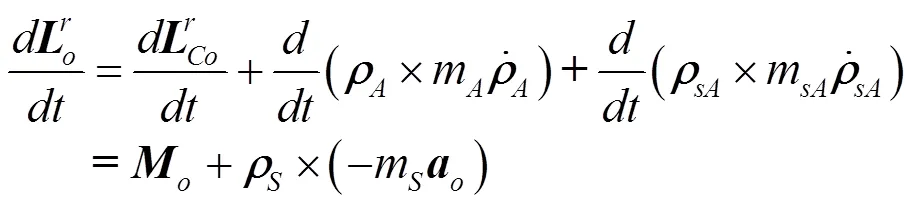
a. 壳体相对动量矩对时间的导数

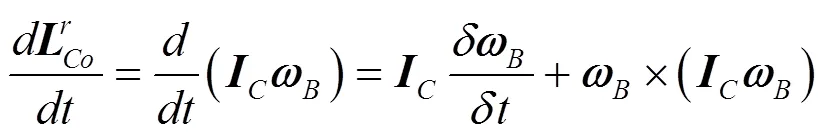
b. 质量块相对动量矩对时间的导数

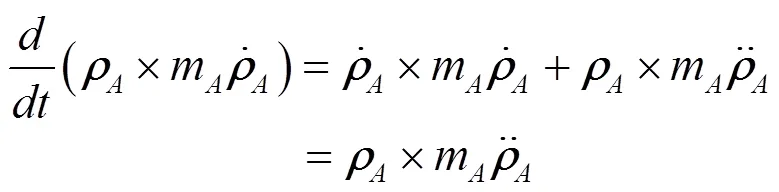
c. 不可动部分相对动量矩对时间的导数

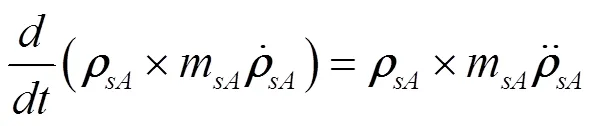
d. 合外力对壳体质心的力矩

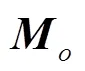
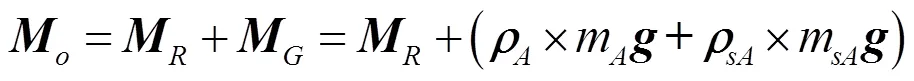
e. 牵连惯性力矩

牵连惯性力矩可表示为：

将上述各项代入式（16），可得：

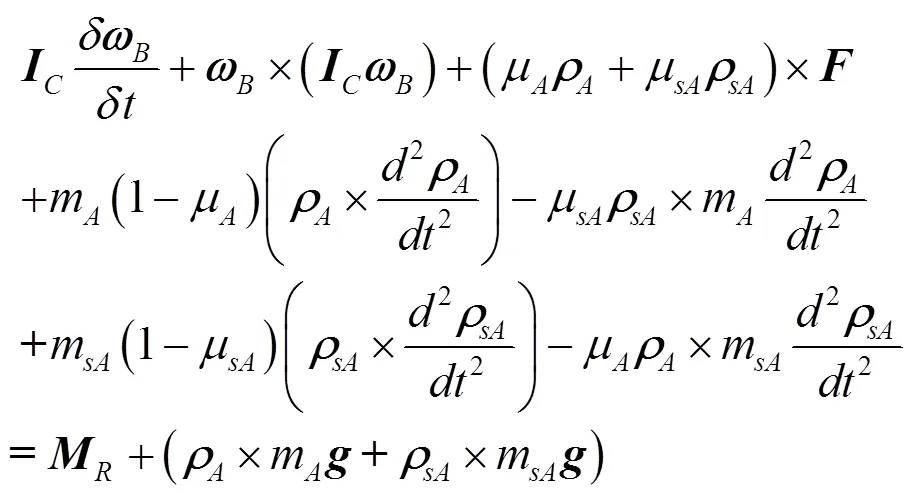
设质量块和不可动部分初始安装位置质心重合，根据矢量求导法则和矢量叉乘运算法则，将力和力矩表达式代入式（22），化简可得绕壳体质心转动动力学方程的矢量形式为：

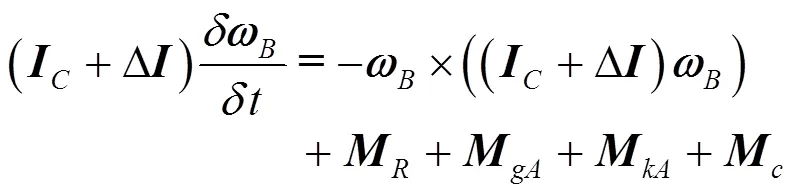
3 飞行器特性分析

由理论力学可知，当质量块相对壳体运动时，所产生的惯性力会影响质心运动。由于变质心机构质心的偏移，不仅使飞行器转动惯量发生变化，也引入了惯性力矩的干扰，从而影响飞行器的姿态运动。因此，一维变质心飞行器具有更加复杂的动力学方程，有必要分析其模型特性。

3.1 飞行器动力学分析

3.1.1 轨道动力学分析

一维变质心再入飞行器所受外力包括气动力、地球引力以及由变质心机构运动引入的惯性力。

a. 气动力

一维变质心再入飞行器所受气动力大小与飞行器动压及气动系数成正比。由于高空段空气密度较小，因此飞行器动压较小。同时，飞行器俯仰与偏航通道依靠自身静稳定度保持稳定，因此其气动系数也较小，此时飞行器所受的空气动力不大。随着再入段飞行器高度的高速下降，空气密度迅速增大，动压与空气动力也急剧增长，成为飞行器运动的最主要影响因素。

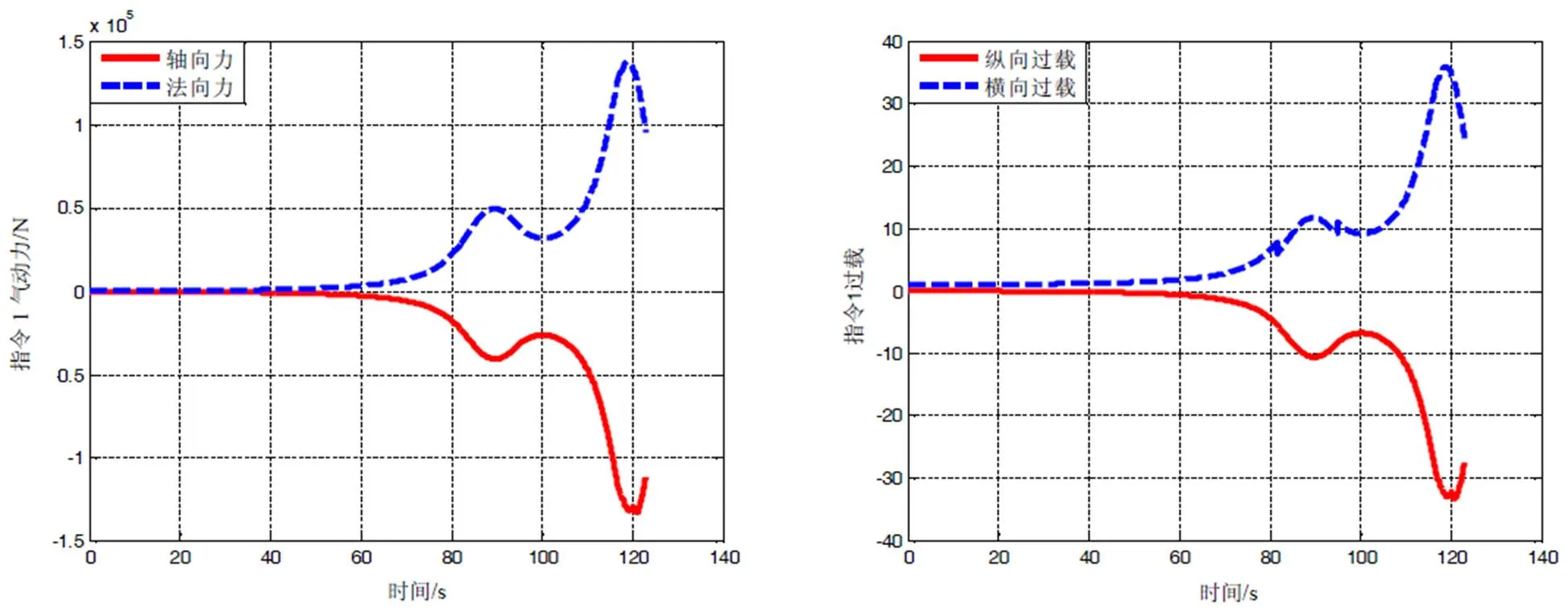
图3 飞行器气动力与各向过载变化曲线

对飞行器法向力和轴向力进行仿真，仿真曲线如图3所示。可以看到，随着高度下降，飞行器动压增大，各向空气动力随之增大。在40km以上的高空，轴向力与法向力最大值约3000N，随着高度下降，各向气动力增加，轴向力与法向力最大量级为105。

b. 地球引力

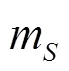
c. 变质心机构惯性力

通过以上分析可知，对于一维变质心再入飞行器的弹道，在高空段主要受地球引力影响，在40km以下，主要受气动力影响。而变质心机构惯性力则对弹道影响较小，可通过力量级比较对弹道运动适当简化。

3.1.2 姿态动力学分析

由动力学模型可知，飞行器姿态运动中所受力矩主要包括气动力矩、陀螺力矩、变质心机构控制力矩以及惯性力矩。此外，由于飞行器系统转动惯量与惯性主轴的改变，还将引入各通道姿态运动的耦合。下面逐一进行仿真分析。

a. 气动力矩

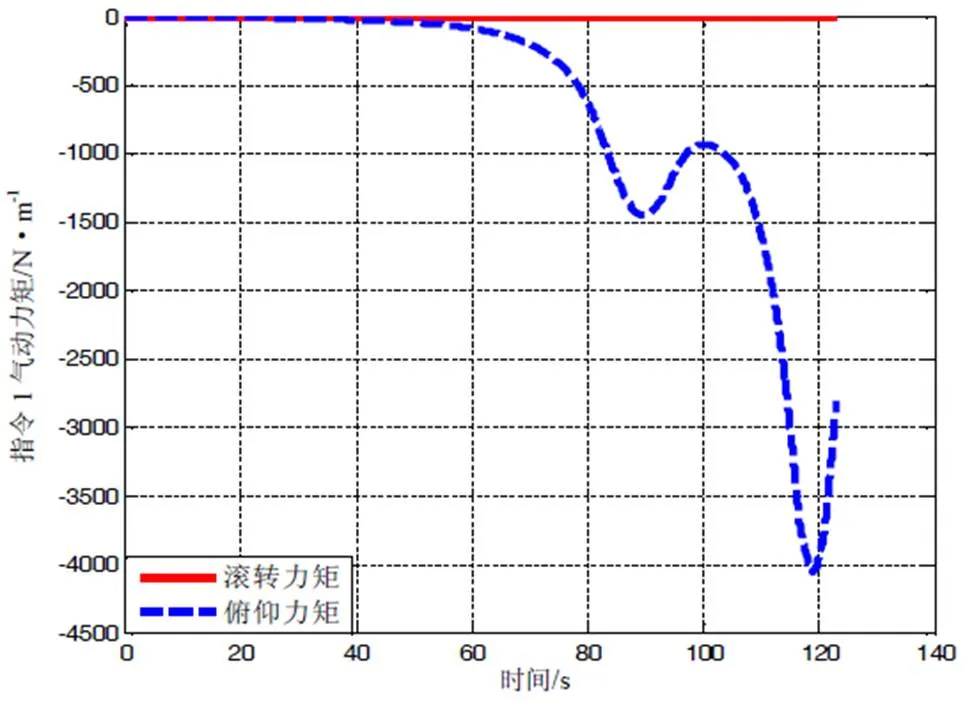
图4 飞行器滚转力矩与俯仰力矩随高度变化曲线

飞行器气动力矩大小主要取决于飞行器气动角和动压。以飞行器壳体质心为参考点，从图4的仿真曲线可以看到，随着飞行器高度下降，飞行器俯仰力矩可达103量级，因此气动力矩是影响飞行器姿态的主要因素。

b. 陀螺力矩

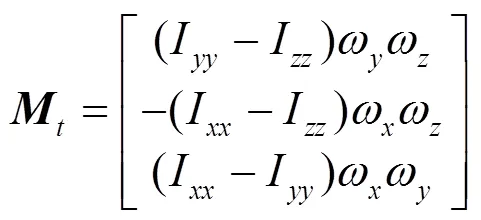
c. 控制力矩

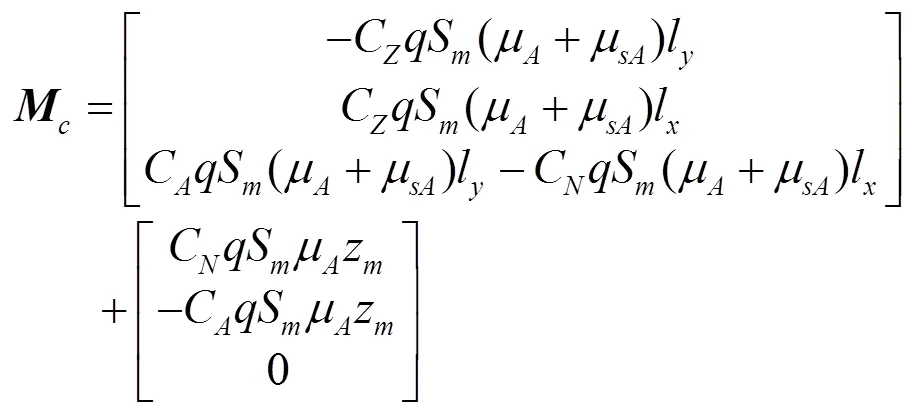
可以看出，控制力矩包括两部分，一是由质量块初始安装位置引起的附加气动力矩，可对飞行器的气动力矩进行平衡；二是由质量块主动移动引起的控制力矩，可对飞行器姿态进行主动调节。假设变质心机构初始位置，结合飞行器飞行弹道，仿真得到附加力矩曲线如图5所示。

通过曲线可知，附加气动力矩是影响飞行器姿态的主要因素之一，对飞行器起着姿态控制作用，且随着动压的增大而增大。由于控制耦合的存在，质量块运动会为偏航通道引入附加气动力矩，其量级与滚转通道控制力矩相当。由于飞行器偏航通道转动惯量约为滚转通道转动惯量的10倍，且在实际飞行控制中，质量块并非持续做大幅运动，因此偏航通道在侧向静稳定性下可保证振荡收敛。

d.惯性力矩

质量块的运动将导致飞行器受到变质心机构惯性力的作用，当变质心机构与飞行器质心存在位置偏差时，惯性力将以惯性力矩的形式被引入飞行器绕质心运动中，惯性力矩表达式为：

e.惯量耦合

由于质量块运动将导致飞行器总质心偏移，飞行器总转动惯量将发生变化，而转动惯量的变化将会进一步加强各通道间的运动耦合与控制耦合。质量块运动对系统转动惯量的影响主要体现在两个方面，一是改变了惯性主轴转动惯量大小；二是改变了惯性主轴位置，产生了惯量积。

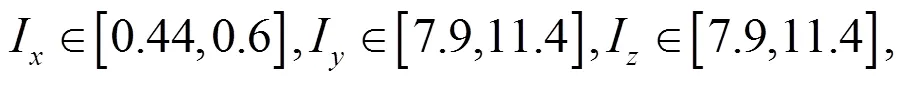
由此可见，质量块的运动使主惯量轴上的转动惯量增大，各惯量轴上变化范围不超过5%。质量块运动主要增大了滚转与偏航通道以及滚转与俯仰通道间的惯量积，而对偏航与俯仰通道的影响较小。

3.2 飞行器控制能力分析

由3.1.2c分析可知，控制力矩表达式的第一部分为机构安装位置引入的附加气动力矩，主要用来平衡飞行器气动力矩；第二部分为控制力矩，用来主动调节飞行器姿态。控制力矩的大小直接决定了飞行器滚控响应的快速性。

结合飞行器姿态方程，俯仰与偏航通道仍采用“瞬时平衡”假设，可得控制力矩作用下飞行器滚转角加速度表达式为：

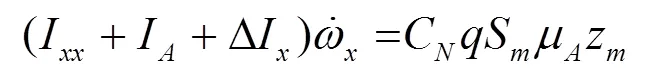
将上式作为一维变质心滚控飞行器控制能力的衡量指标，对其进行仿真分析，仿真曲线如图6所示。

仿真曲线表明，由于40km以上的动压较小，飞行器最大滚动控制力矩较小。但随着高度下降，动压增大，飞行器最大滚控力矩与最大滚转角加速度明显增大，其量级为10。因此，变质心控制的优越性主要体现在低空（40km以下）段。

4 结束语

a. 变质心控制机构处于飞行器内部，因而无需特殊解决控制机构的烧蚀问题，同时也减少了某些控制参数的时变性；

b. 飞行器俯仰与偏航姿态均为振荡收敛状态，其收敛点为各通道配平角，对于侧滑即为零侧滑角；

c. 飞行器弹道主要受气动力与地球引力影响，变质心机构运动产生的惯性力对其影响较小；

d. 随着高度下降，飞行器最大滚控力矩与最大滚转角加速度明显增大。因此，变质心控制的优越性主要体现在低空段；

e. 利用高速气动力和气动力矩进行姿态控制，只要设计合理，在同样姿态控制要求下，可最大限度地节约能源，提高飞行器有效载荷的携带能力；

f. 只要飞行器的质心有很小的变化，就能改变飞行器静稳定度，产生足够的过载改变飞行器的飞行轨迹，为控制系统提供了一种方便有效的作动方式，大大提高了飞行器的机动能力。

1 Petsopoulo T, Regan F J. A moving-mass roll control system for a fixed-trim re-entry vehicle [C]. The 32nd Aerospace Science Meeting and Exhibit, Reno, US, January, 1994: 10～13

2 Petsopoulos T, Regan F J. Moving-mass roll control system for fixed-trim re-entry vehicle [J]. Journal of Spacecraft and Rockets, 1996, 33(1): 54～61

3 高长生，李君龙，荆武兴，等. 导弹质量矩控制技术发展综述[J]. 宇航学报，2010，31(2)：307～314

4 Anon. Generic aerocapture atmospheric entry study, volume 1 (final report) [R]. US: General Electric Co., October 1980

5 Regan F J, Kavetsky R A. Add-on controller for ballistic reentry vehicle [J]. IEEE Transactions on Automatic Control, 1984, 12(6): 869～880

6 White J E, Robinett R D. Principal axis misalignment control for deconing of spinning spacecraft [J]. Journal of Guidance, Control and Dynamics, 1994, 17(4): 823～830

7 Norris R, Kristensen H. Russian nuclear force[J]. Bulletin of the Atomic Scientists, 2005, 61(2): 70～72

8 易彦，周凤岐，周军. 基于变质心控制导弹的运动分析[J]. 航天控制，2000(3)：1～5

9 周军，王霄婷，林鹏. 三维变质心非交互控制的可实现性分析[J]. 宇航学报，2013，34(3)：1000～1328

10 陈升泽，张旋，解春雷，等. 基于反演设计的变质心飞行器滑模变结构控制器设计[J]. 导弹与航天运载技术，2018，362(4)：65～69

11 高长生，陈尔康，荆武兴. 高超声速飞行器机动规避轨迹优[J]. 哈尔滨工业大学学报，2017，49(4)：16～21

12 刘智陶，李涧青，高长生. 欠驱动变质心飞行器的滚偏耦合自抗扰控制[J/OL]. 北京航空航天大学学报：1-10[2020-11-11]. https://doi.org/10.13700/j.bh.1001-5965.2020.0206.

Modeling and Characteristic Analysis of Hypersonic Reentry Vehicle with Moving Mass Control

Fan Boxuan1Chen Guiming1Lin Hongtao2

(1. Rocket Force University of Engineering, Xi’an 710025；2. Unit 31004 of the People’s Liberation Army, Beijing 100091)

This paper establishes a complete dynamic model of a one-dimensional variable-centre-rolling hypersonic reentry vehicle. Research on the trajectory and attitude dynamics of the variable-cent-of-mass aircraft, and clarify the control mechanism and characteristics of the variable-cent-of-mass roll control aircraft. At the same time, the structural design of the aircraft is proposed for the analysis of the coupling effect between the channels and the influence of the actuator parameter settings on the control ability. The related requirements of control system design provide a theoretical basis for the engineering practice of hypersonic reentry aircraft.

hypersonic reentry vehicle；moving mass control；dynamics

樊博璇（1987），博士，兵器科学与技术专业；研究方向：武器系统运用与保障工程。

2020-09-23