基本不等式在高考题中的应用

贾 林

(江苏省苏州市昆山市周市高级中学 215300)

基本不等式及其应用是高中数学中的一个重要知识点，作为一个基本工具，用来破解一些相关问题的最值或取值范围问题，一直是高考数学中的一个热点与交汇点.本文仅就2018年高考题，看一下基本不等式在各种题型中的应用.

一、代数式的最值问题

点评在求解相应代数式的最值问题时，要结合代数式的特征加以合理变形，创造利用基本不等式的条件，主要通过配方、拆添项、配凑因子和平方等技巧变形，确定“一正、二定、三相等”的条件，进而利用基本不等式来确定最值即可.

二、三角函数的最值问题

例2(2018·全国Ⅰ理·16)已知函数f(x)=2sinx+sin2x，则f(x)的最小值是____.

分析通过三角关系式的巧妙转化，再结合配凑，同时利用基本不等式来处理两个平行的三角关系式，进而得以确定相应的最值问题.

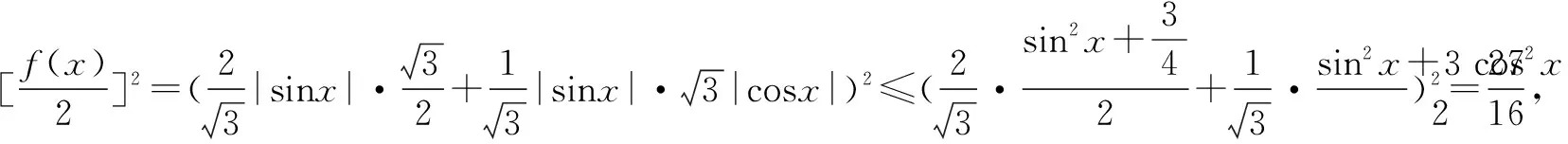
点评基本不等式也是解决三角函数最值的一大工具，其解决的思维关键是巧妙进行转化，特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用.

三、解三角形的最值问题

例3(2018·江苏·13)在△ABC中，角A，B，C所对的边分别为a，b，c，∠ABC=120°，∠ABC的平分线交AC于点D，且BD=1，则4a+c的最小值为____.

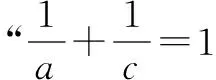
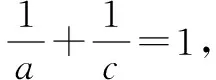
点评在利用基本不等式破解解三角形问题时，关键是利用三角形的特征来建立有关边、角的定值问题，为利用基本不等式提供条件.对于解三角形与基本不等式的交汇与综合，是两者考查的热点之一，是命题者比较热衷的考点之一.

四、圆锥曲线的最值问题

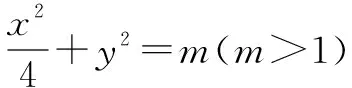
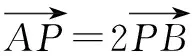
综上分析，可知当m=5时，点B横坐标的绝对值最大为2，故填：5.

点评圆锥曲线中的最值问题的破解，基本不等式是其中一个重要工具，也是圆锥曲线最值求解的最常见的思维方式之一，解决问题的关键也是建立相应的定值条件，注意参数的取值情况，利用基本不等式时要考虑相应的条件与圆锥曲线限制条件之间的关系.

五、综合应用的最值问题

分析常规方法是利用几何法，结合单位圆、平面向量、三角函数、点到直线的距离公式等，解决起来比较繁琐.而利用不等式的相关知识来转化与处理，显得简单快捷.

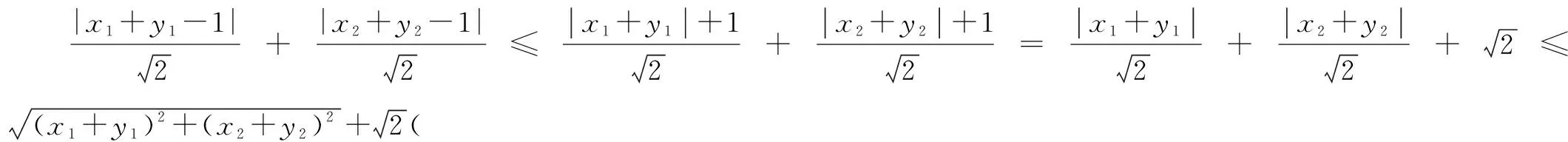
点评通过本题的解析过程可知，这里根据绝对值关系式的性质，用到的相关数学知识：(1)绝对值不等式的性质；(2)基本不等式的变形公式；(3)排序不等式等.用到相关不等式的性质时，巧妙性较强，思维方式独特，具体求解过程中往往难以涉及.而利用以上求解过程，处理起来更为简单快捷.

基本不等式的应用可以非常有效快捷地解决一些最值或取值范围问题，在历年高考中出现的频率非常高，难度有时大有时小.正确掌握基本不等式以及对应的变形公式，并会根据题目条件加以合理转化与变形，为创设利用基本不等式的应用提供条件，并不断拓展解题视点，开拓解题思维，提升数学能力.